L4 Advance Language Models高级语言模型
Advance Language Models高级语言模型
- [Generalisation of Language Models 语言模型的泛化](#Generalisation of Language Models 语言模型的泛化)
- 泛化解决方法
-
- [Laplace smoothing 拉普拉斯平滑-Add-One Estimation](#Laplace smoothing 拉普拉斯平滑-Add-One Estimation)
- [Interpolation and backoff 插值和回退](#Interpolation and backoff 插值和回退)
-
- [更好的方法:线性插值(Linear Interpolation)](#更好的方法:线性插值(Linear Interpolation))
- [Open vs. Closed Vocabulary Tasks 开放或者封闭的词汇任务](#Open vs. Closed Vocabulary Tasks 开放或者封闭的词汇任务)
- [语言模型(Language Model, LM)里如何处理 OOV(Out-of-Vocabulary)词](#语言模型(Language Model, LM)里如何处理 OOV(Out-of-Vocabulary)词)
- [Good Turing Smoothing 良好的图灵平滑](#Good Turing Smoothing 良好的图灵平滑)
-
- 核心公式
- [Good--Turing 的"尾部问题"与 Simple Good--Turing(SGT)](#Good–Turing 的“尾部问题”与 Simple Good–Turing(SGT))
- [Kneser-Ney Smoothing Kneser--Ney平滑](#Kneser-Ney Smoothing Kneser–Ney平滑)
-
- [Kneser--Ney 平滑公式](#Kneser–Ney 平滑公式)
- [归一化常数 λ ( w i − 1 ) \lambda(w_{i-1}) λ(wi−1)](#归一化常数 λ ( w i − 1 ) \lambda(w_{i-1}) λ(wi−1))
- 延续概率 (Continuation Probability)
Generalisation of Language Models 语言模型的泛化
记住一个语言模型,无论是 n-gram 语言模型,还是神经语言模型。
最终,它是一个将概率与序列相关联的模型。最常见的方法是使用这个最大似然估计(Maximum Likelihood Estimate, MLE)
Maximum Likelihood Estimate (MLE):
P ( w i ∣ w i − 1 ) = c o u n t ( w i − 1 , w i ) c o u n t ( w i − 1 ) P(w_i \mid w_{i-1}) = \frac{count(w_{i-1}, w_i)}{count(w_{i-1})} P(wi∣wi−1)=count(wi−1)count(wi−1,wi)
例如:
P ( the ∣ in ) = c o u n t ( " i n t h e " ) c o u n t ( " i n " ) P(\text{the} \mid \text{in}) = \frac{count("in \; the")}{count("in")} P(the∣in)=count("in")count("inthe")
我们需要考虑在未见过的数据(unseen data)中出现新 n-gram 的可能性。
莎士比亚二元组
莎士比亚语料库中,
N = 884 , 647 N = 884,647 N=884,647 tokens
V = 29 , 066 V = 29,066 V=29,066 types ⇒ V 2 ≈ 845 M \;\;\Rightarrow\;\; V^{2} \approx 845M ⇒V2≈845M possible bigrams!
计算的二元组有845M个,但实际只产生了~300,000二元组 type(占全部可能的二元组的 4%)。我们将拥有96%从未见过的二元组,不会有任何统计数据,数据是0。
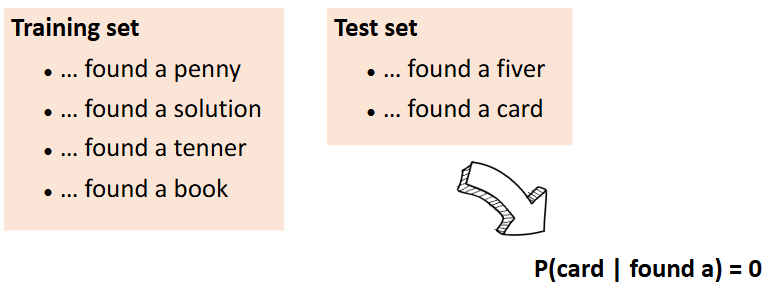
这就会导致,如果在原语料库里没有见过,概率就会是0。即使这个词组出现是非常合理的。而且与此word相关的多元组的概率都会是0,因为相乘。所以,我们需要泛化能力。
泛化解决方法
解决泛化问题的方法是 smoothing 平滑。
Laplace smoothing 拉普拉斯平滑-Add-One Estimation
拉普拉斯平滑是最直接的平滑之一。本质就是给字典中的每一个词都加了一次出现的次数。
MLE estimate:
P M L E ( w i ∣ w i − 1 ) = c ( w i − 1 , w i ) c ( w i − 1 ) P_{MLE}(w_i \mid w_{i-1}) = \frac{c(w_{i-1}, w_i)}{c(w_{i-1})} PMLE(wi∣wi−1)=c(wi−1)c(wi−1,wi)
Add-one estimate:
P Add-1 ( w i ∣ w i − 1 ) = c ( w i − 1 , w i ) + 1 c ( w i − 1 ) + V P_{\text{Add-1}}(w_i \mid w_{i-1}) = \frac{c(w_{i-1}, w_i) + 1}{c(w_{i-1}) + V} PAdd-1(wi∣wi−1)=c(wi−1)+Vc(wi−1,wi)+1
举例
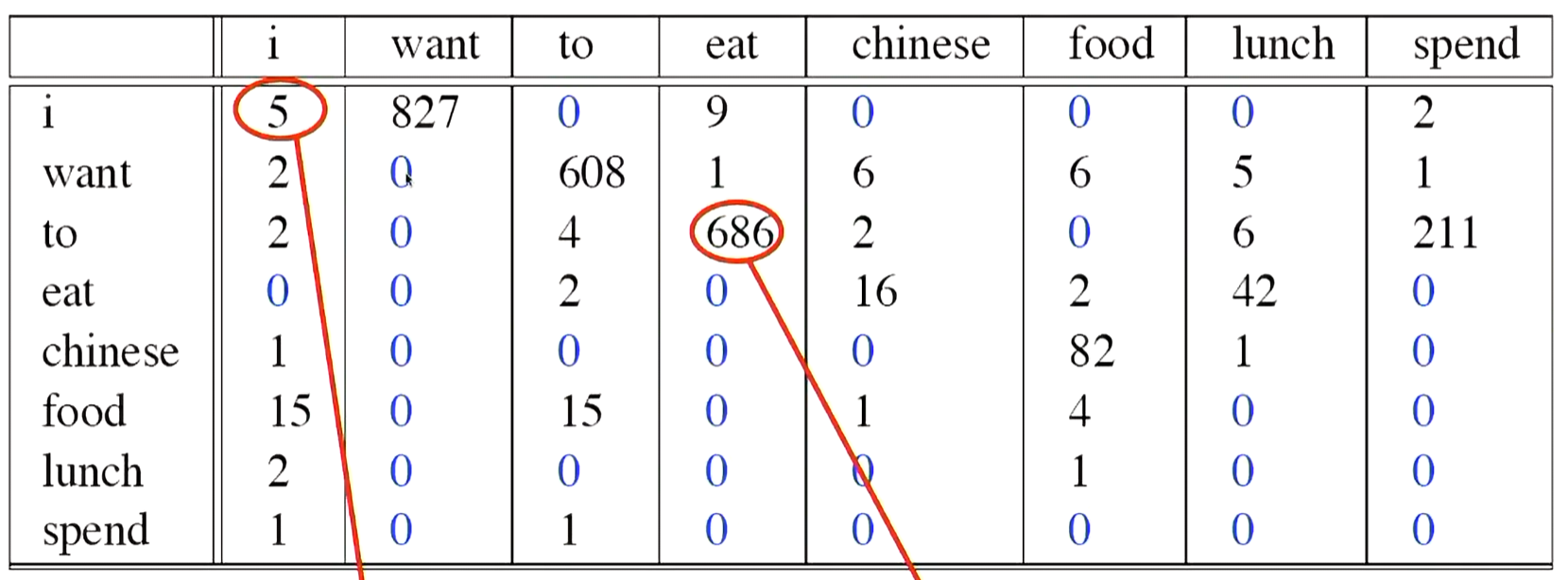
进行拉普拉斯平滑后,
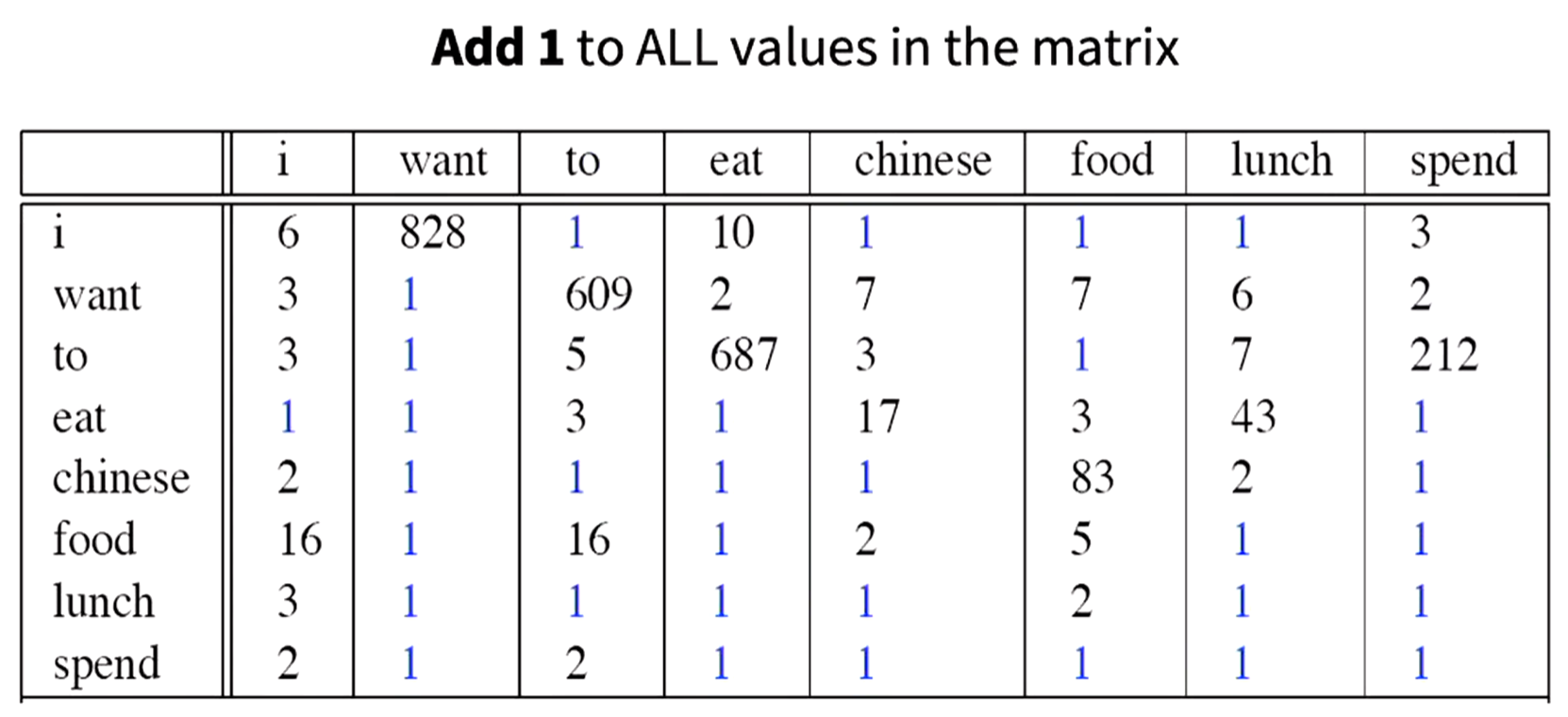
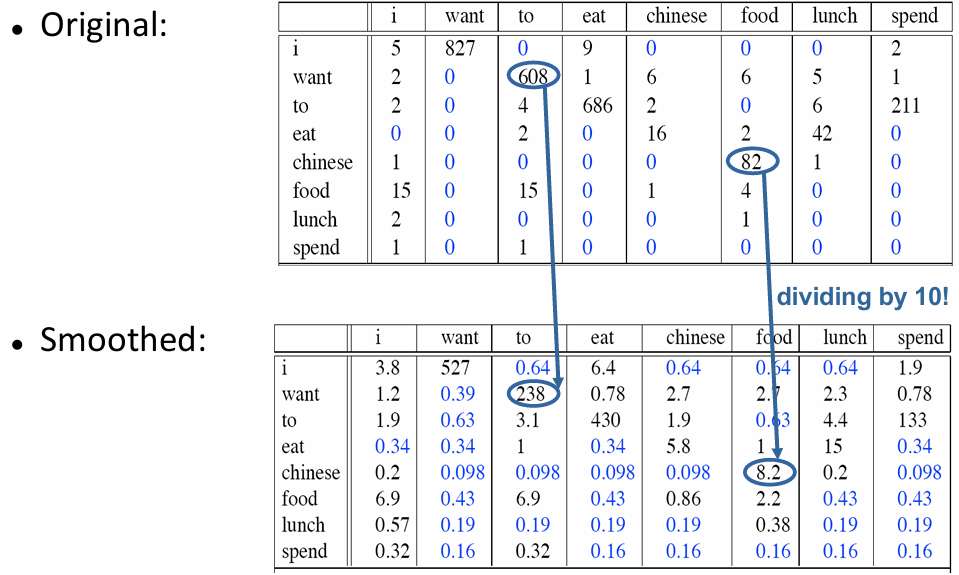
计算概率表,

可以看到,原本概率为0,都有用了概率,它们非常小,比如0.00042。这就很好,因为不会再抵消我们的乘法。
重组计数
无需同时更改分子和分母,定义一个计数 C ∗ C* C∗可以解决。
P ∗ ( w n ∣ w n − 1 ) = C ( w n − 1 w n ) + 1 C ( w n − 1 ) + V = C ( w n − 1 w n ) ∗ C ( w n − 1 ) P^{*}(w_{n} \mid w_{n-1}) = \frac{C(w_{n-1}w_{n}) + 1}{C(w_{n-1}) + V} = \frac{C(w_{n-1}w_{n})^{*}}{C(w_{n-1})} P∗(wn∣wn−1)=C(wn−1)+VC(wn−1wn)+1=C(wn−1)C(wn−1wn)∗
C ( w n − 1 w n ) ∗ = [ C ( w n − 1 w n ) + 1 ] × C ( w n − 1 ) C ( w n − 1 ) + V C(w_{n-1}w_{n})^{*} = \frac{\left[ C(w_{n-1}w_{n}) + 1 \right] \times C(w_{n-1})}{C(w_{n-1}) + V} C(wn−1wn)∗=C(wn−1)+V[C(wn−1wn)+1]×C(wn−1)
只是另一种数学形式
Add---K
拉普拉斯给了一点灵活性,不是只能添加一个。可以根据需要添加任意数量、更多或
少。所以现在只需放置一个 k k k 因子,而不是1。
Laplace Smoothing的问题
它通常不是语言模型的最佳解决方案。有了如此稀疏的矩阵,我们用 1 替换了太多的 0。有的二元组分享了太多,对它的准确率造成了影响。
仍然经常用于 NLP 任务,特别是当我们观察到 0 较少时。
Interpolation and backoff 插值和回退
为了解决,在MLE中分母为0的问题,这个二元组就没有出现计数过,
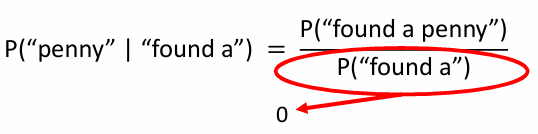
我们可以这样近似,

更好的方法:线性插值(Linear Interpolation)
一种更好的解决方案是将所有概率混合起来:unigram、bigram、trigram 等。
为此,我们需要一组正的权重系数 λ 0 , λ 1 , ... , λ n − 1 \lambda_0, \lambda_1, \ldots, \lambda_{n-1} λ0,λ1,...,λn−1,
并且满足:
∑ i λ i = 1 \sum_i \lambda_i = 1 i∑λi=1
例如:
P ^ ( "penny" ∣ "found a" ) ≈ λ 2 P ( "penny" ∣ "found a" ) + λ 1 P ( "penny" ∣ "a" ) + λ 0 P ( "a" ) \hat{P}(\text{"penny"} \mid \text{"found a"}) \approx \lambda_2 P(\text{"penny"} \mid \text{"found a"})\\+ \lambda_1 P(\text{"penny"} \mid \text{"a"})\\+ \lambda_0 P(\text{"a"}) P^("penny"∣"found a")≈λ2P("penny"∣"found a")+λ1P("penny"∣"a")+λ0P("a")
Open vs. Closed Vocabulary Tasks 开放或者封闭的词汇任务
处理保留数据或测试数据时的两种情况:
- We know ALL words in advance.我们事先知道所有单词 。
i.e. all words were also in training data.也就是说,所有单词都包含在训练数据中。
We have a fixed vocabulary V -- closed vocab. Task 我们有一个固定的词汇表 V -- 封闭词汇表任务 - We may find new, unseen words (generally the case) 我们可能会发现新的、未见过的单词 (通常情况下)
Out Of Vocabulary (OOV) words -- open vocab. task 超出词汇表 (OOV) 的单词 -- 开放词汇表任务
语言模型(Language Model, LM)里如何处理 OOV(Out-of-Vocabulary)词
OOV(未登录词/词表外词):指在训练词表(lexicon)里不存在的单词,比如新造词、拼写错误、罕见专有名词等。
解决方法:在词表里专门加一个特殊标记 <OOV> \text{<OOV>} <OOV>。
训练时:
先创建一个固定大小的词表 L L L(大小为 V V V)。
在预处理文本时,把所有 不在 L L L 中的词替换成 <OOV> \text{<OOV>} <OOV>。
训练语言模型时, <OOV> \text{<OOV>} <OOV> 就和其他词一样,作为普通的 token。
测试时:
对于没见过的新词,也会映射成 <OOV> \text{<OOV>} <OOV>,并赋予 <OOV> \text{<OOV>} <OOV> 的概率。
Good Turing Smoothing 良好的图灵平滑
图灵平滑关键是Frequency of frequency 频数的频率
N c N_c Nc = count of tokens observed c c c times 观察到 c c c 次的toekns的types的数量
例如: I am happy and I am fine and I have to go
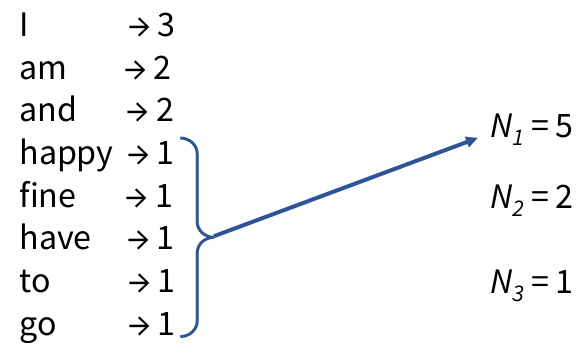

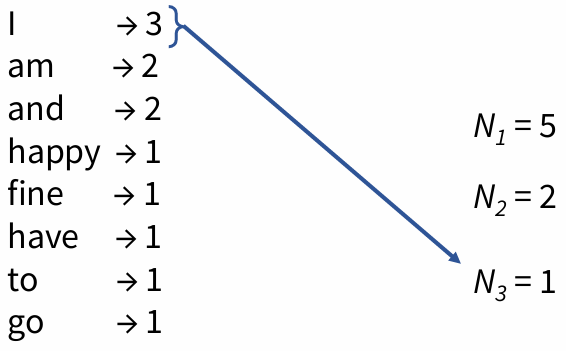
对应频率的频率(Frequency of Frequency):
N 1 = 5 , N 2 = 2 , N 3 = 1 N_1 = 5, \quad N_2 = 2, \quad N_3 = 1 N1=5,N2=2,N3=1
因为出现1次的tokens有5个types,所以 N 1 = 5 N_1 = 5 N1=5
此时,
N N N是整个语料库的单词总数。 N = 3 + 2 + 2 + 1 + 1 + 1 + 1 + 1 = 12 N =3+2+2+1+1+1+1+1=12 N=3+2+2+1+1+1+1+1=12,也等于 N = ∑ r N r = 3 N 3 + 2 N 2 + 1 N 1 = 3 × 1 + 2 × 2 + 5 × 1 = 12 N=\sum rN_r = 3N_3+2N_2+1N_1=3\times1+2\times2+5\times1=12 N=∑rNr=3N3+2N2+1N1=3×1+2×2+5×1=12
I 的数量为3,概率为 3 12 \frac{3}{12} 123
核心公式
S r S_{r} Sr 的计算公式为: S r = r × N r S_{r} = r \times N_{r} Sr=r×Nr
其中:
- r r r :某个 n-gram 出现的次数
- N r N_{r} Nr :恰好出现 r r r 次的不同 n-gram 的数量
如果有 N r N_{r} Nr 个不同的 n-gram,每个都出现 r r r 次,那么这些 n-gram 的 总出现次数 就是: r N r rN_{r} rNr
对于一个=出现 r 次的 n-gram正常概率公式:
P ( c = r ) = r N P(c = r) = \frac{r}{N} P(c=r)=Nr
对于一个出现 r r r 次的 n-gram, Good-Turing 概率估计公式为:
P G T ( c = r ) = ( r + 1 ) N r + 1 N × N r P_{GT}(c = r) = \frac{(r+1)N_{r+1}}{N \times N_{r}} PGT(c=r)=N×Nr(r+1)Nr+1
其中:
- r r r :某个 n-gram 出现的次数
- N r N_{r} Nr :恰好出现 r r r 次的不同 n-gram 数量
- N N N :语料库中所有 n-gram 的总数

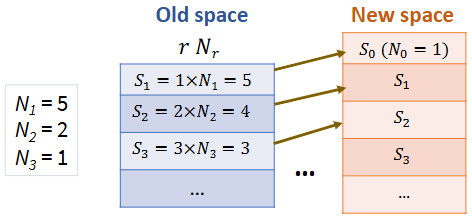
P G T ( c = 0 ) = 1 N × ( 0 + 1 ) N 0 + 1 N 0 = N 1 N = 5 12 P_{GT}(c = 0) = \frac{1}{N} \times\frac{(0+1)N_{0+1}}{N_{0}}=\frac{N_1}{N}=\frac{5}{12} PGT(c=0)=N1×N0(0+1)N0+1=NN1=125
P G T ( c = 1 ) = 1 N × ( 1 + 1 ) N 1 + 1 N 1 = 1 12 × 2 × 2 5 = 0.8 12 P_{GT}(c = 1) = \frac{1}{N} \times\frac{(1+1)N_{1+1}}{N_{1}}=\frac{1}{12}\times\frac{2\times2}{5}=\frac{0.8}{12} PGT(c=1)=N1×N1(1+1)N1+1=121×52×2=120.8
P G T ( c = 2 ) = 1 N × ( 2 + 1 ) N 2 + 1 N 2 = 1 12 × 3 × 1 1 = 3 12 P_{GT}(c = 2) = \frac{1}{N} \times\frac{(2+1)N_{2+1}}{N_{2}}=\frac{1}{12}\times\frac{3\times1}{1}=\frac{3}{12} PGT(c=2)=N1×N2(2+1)N2+1=121×13×1=123
P G T ( c = 3 ) = 1 N × ( 3 + 1 ) N 3 + 1 N 3 = 1 12 × 4 × N 4 1 = 4 N 4 12 P_{GT}(c = 3) = \frac{1}{N} \times\frac{(3+1)N_{3+1}}{N_{3}}=\frac{1}{12}\times\frac{4\times N_4}{1}=\frac{4N_4}{12} PGT(c=3)=N1×N3(3+1)N3+1=121×14×N4=124N4
图灵平滑本质是:把分子重新分配,分母保持不变(Laplace Smoothing是分子+1,分母+V,很简单,但有的影响很大)
怎么处理 N 4 = 0 N_4 = 0 N4=0 的情况?
原始 Good--Turing :当 N r + 1 = 0 N_{r+1}=0 Nr+1=0 时,不再用 GT,而是直接用 MLE:
p ( w ∣ c = 3 ) ≈ 3 N p(w \mid c=3) \approx \frac{3}{N} p(w∣c=3)≈N3
Simple Good--Turing(SGT) :对 N r N_r Nr 做平滑 (回归/插值),得到一个估计的 N ^ 4 > 0 \hat N_4>0 N^4>0,再代入公式:
单个出现 3 3 3 次的 n-gram 概率:
p SGT ( w ∣ c = 3 ) = ( 3 + 1 ) N ^ 4 N N ^ 3 p_{\text{SGT}}(w \mid c=3)=\frac{(3+1)\,\hat N_{4}}{N \,\hat N_{3}} pSGT(w∣c=3)=NN^3(3+1)N^4
Good--Turing 的"尾部问题"与 Simple Good--Turing(SGT)
问题:当 r r r 很大时 N r + 1 = 0 N_{r+1}=0 Nr+1=0
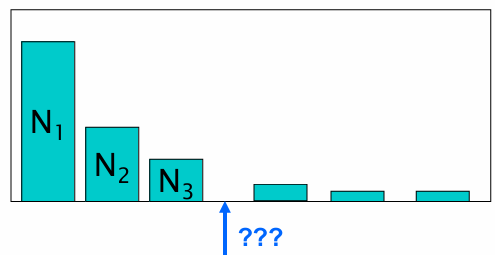
例:单词 and 的计数 r = 12156 r=12156 r=12156。
经典 Good--Turing 需要用折扣计数
r ∗ = ( r + 1 ) N r + 1 N r r^*=\frac{(r+1)N_{r+1}}{N_r} r∗=Nr(r+1)Nr+1
但对这么大的 r r r,几乎不可能还有 "恰好出现 r + 1 = 12157 r+1=12157 r+1=12157 次" 的词, N r + 1 N_{r+1} Nr+1 往往为 0,导致公式**失效/不稳定**。
现象:计数的计数 N 1 , N 2 , N 3 , ... N_1,N_2,N_3,\ldots N1,N2,N3,... 随 r r r 增大变得稀疏 ,很多 N r + 1 N_{r+1} Nr+1 直接为 0。
解决:Simple Good--Turing(Gale & Sampson)
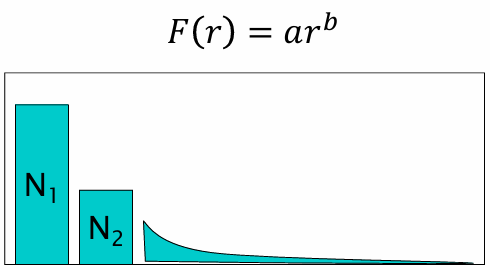
思路:不要直接用不可靠的 N r N_r Nr ,而用一条幂律曲线 去拟合尾部:
F ( r ) = a r b ( b < − 1 ) F(r)=a\,r^{\,b}\qquad (b< -1) F(r)=arb(b<−1)
在 log N r \log N_r logNr 对 log r \log r logr 上做线性回归,求得 a , b a,b a,b,得到平滑后的
N ^ r = F ( r ) , N ^ r + 1 = F ( r + 1 ) . \hat N_r = F(r),\qquad \hat N_{r+1}=F(r+1). N^r=F(r),N^r+1=F(r+1).
用平滑值代入 GT,得到折扣计数与概率:
r ∗ = ( r + 1 ) N ^ r + 1 N ^ r , p SGT ( w ∣ c = r ) = r ∗ N . r^*=\frac{(r+1)\hat N_{r+1}}{\hat N_r},\qquad p_{\text{SGT}}(w\mid c=r)=\frac{r^*}{N}. r∗=N^r(r+1)N^r+1,pSGT(w∣c=r)=Nr∗.
未见事件 ( r = 0 r=0 r=0)的总概率质量:
P 0 = N ^ 1 N . P_0=\frac{\hat N_1}{N}. P0=NN^1.
Kneser-Ney Smoothing Kneser--Ney平滑
Kneser--Ney(KN)的根本目的,主要是为了解决 高阶 n-gram(比如 bigram、trigram) 的概率为 0 的问题,而不是 unigram。
根据上文,进行概率处理。
Kneser--Ney 平滑公式
二元组概率公式为:
P K N ( w i ∣ w i − 1 ) = max ( c ( w i − 1 , w i ) − d , 0 ) c ( w i − 1 ) + λ ( w i − 1 ) P cont ( w i ) P_{KN}(w_i \mid w_{i-1}) = \frac{\max(c(w_{i-1}, w_i) - d, 0)}{c(w_{i-1})}+ \lambda(w_{i-1}) P_{\text{cont}}(w_i) PKN(wi∣wi−1)=c(wi−1)max(c(wi−1,wi)−d,0)+λ(wi−1)Pcont(wi)
其中:
- c ( w i − 1 , w i ) c(w_{i-1}, w_i) c(wi−1,wi) :bigram ( w i − 1 , w i ) (w_{i-1}, w_i) (wi−1,wi) 的出现次数 (token 数)
- c ( w i − 1 ) c(w_{i-1}) c(wi−1) :unigram w i − 1 w_{i-1} wi−1 的出现次数 (token 数)
- d d d :折扣常数
- P cont ( w i ) P_{\text{cont}}(w_i) Pcont(wi) :延续概率(continuation probability)
归一化常数 λ ( w i − 1 ) \lambda(w_{i-1}) λ(wi−1)
λ ( w i − 1 ) \lambda(w_{i-1}) λ(wi−1) 是一个归一化常数,用来分配被折扣掉的概率质量:
λ ( w i − 1 ) = d c ( w i − 1 ) ⋅ ∣ { w : c ( w i − 1 , w ) > 0 } ∣ \lambda(w_{i-1}) = \frac{d}{c(w_{i-1})} \cdot |\{ w : c(w_{i-1}, w) > 0 \}| λ(wi−1)=c(wi−1)d⋅∣{w:c(wi−1,w)>0}∣
解释:
- d c ( w i − 1 ) \tfrac{d}{c(w_{i-1})} c(wi−1)d :每个 bigram 的归一化折扣量
- d d d:理论上 0<d<1,常见设定:d=0.75(经验上效果好)
- ∣ { w : c ( w i − 1 , w ) > 0 } ∣ |\{ w : c(w_{i-1}, w) > 0 \}| ∣{w:c(wi−1,w)>0}∣ :能跟在 w i − 1 w_{i-1} wi−1 后出现的不同词 bigram 的数量 (type 数)
延续概率 (Continuation Probability)
在 Kneser--Ney 平滑中,unigram 概率不是用词频,而是用 延续概率 定义为:
P cont ( w ) = ∣ { w i − 1 : c ( w i − 1 , w ) > 0 } ∣ ∣ { ( w j − 1 , w j ) : c ( w j − 1 , w j ) > 0 } ∣ P_{\text{cont}}(w) = \frac{|\{ w_{i-1} : c(w_{i-1}, w) > 0 \}|} {|\{ (w_{j-1}, w_j) : c(w_{j-1}, w_j) > 0 \}|} Pcont(w)=∣{(wj−1,wj):c(wj−1,wj)>0}∣∣{wi−1:c(wi−1,w)>0}∣
解释:
- 分子:多少个不同的前项 w i − 1 w_{i-1} wi−1 曾经和 w w w 组成过 bigram (即 w w w 出现过的不同上下文数量,type 数量)
- 分母:语料中出现过的所有 bigram 类型总数 (type 总数)
因此, P cont ( w ) P_{\text{cont}}(w) Pcont(w) 衡量的是: "词 w w w 在多少种不同的上下文里作为新延续出现过"
双| |是type总数,c()是token数