深度学习——神经网络

在当今人工智能蓬勃发展的时代，深度学习和神经网络已经成为最受关注的技术领域之一。从智能手机的人脸识别到自动驾驶汽车的环境感知，从医疗影像分析到金融风险预测，这些技术正在深刻改变我们的生活和工作方式。本文将带您了解深度学习和神经网络的基本概念、发展历程以及它们之间的关系。

简介

一、机器学习：智能的基石

机器学习是人工智能的核心分支，它使计算机系统能够从数据中"学习"并改进性能，而无需显式编程。想象一下教孩子识别动物：不是通过编写详细的规则（"猫有尖耳朵、长胡须..."），而是通过展示大量图片让他们自己发现规律------这正是机器学习的基本理念。

机器学习的三大主要类型包括：

• 监督学习​ ：使用标记数据训练模型（如图像分类）
• ​无监督学习​ ：发现未标记数据中的模式（如客户细分）
• ​强化学习​ ：通过试错和奖励机制学习（如游戏AI）

二、神经网络：模仿生物大脑的计算模型

神经网络是机器学习的一个重要分支，其灵感来源于生物神经元的工作方式。就像人脑由数十亿个相互连接的神经元组成，人工神经网络由人工神经元（节点）和连接它们的"突触"（权重）构成。

关键组成部分：

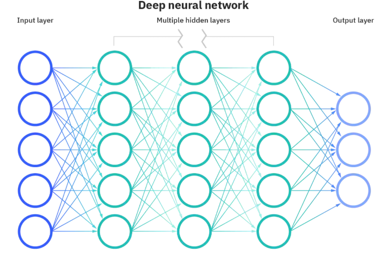
1. ​输入层​ ：接收原始数据
2. 隐藏层​ ：进行特征提取和转换（可能有多层）
3. ​输出层​ ：产生最终预测或分类结果
4. ​激活函数​ ：决定神经元是否"激活"（如ReLU、Sigmoid）
5. 权重​ ：连接强度，通过训练不断调整

1943年，McCulloch和Pitts提出了第一个神经网络数学模型，开启了这一领域的研究。1958年，Frank Rosenblatt发明的感知机(Perceptron)是第一个可学习的神经网络模型。

三、深度学习：神经网络的"深度"进化

深度学习本质上是具有多个隐藏层的神经网络。这里的"深度"指的是网络层次的深度，通常包含多个非线性变换层，能够自动学习数据的多层次抽象表示。

深度学习的突破性进展：

• 特征自动提取​：传统机器学习需要人工设计特征，而深度学习可以自动学习
• ​处理复杂数据​ ：特别适合图像、语音、视频等高维数据
• ​性能突破​ ：在许多任务上达到或超越人类水平

2012年，AlexNet在ImageNet竞赛中大幅领先传统方法，标志着深度学习时代的真正开启。随后，各种深度网络架构如雨后春笋般涌现。

神经网络的构造

一、神经元：神经网络的基本单元

1. 生物神经元与人工神经元对比

• 生物神经元：

• 结构组成：由树突（接收输入信号）、细胞体（整合处理信号）和轴突（传输输出信号）构成
• 工作原理：通过突触传递电化学信号，当输入信号总和超过阈值时产生动作电位
• 典型特性：具有兴奋性、抑制性和可塑性等特征

• 人工神经元（MCP模型）：

• 数学模型：output = activation_function(∑(inputs * weights) + bias)
• 模拟特性：
  • 输入接收：对应生物神经元的树突功能
  • 加权处理：模拟突触强度（权重）对信号的影响
  • 激活输出：类似细胞体的阈值激活机制
• 示例：感知机(Perceptron)是最简单的人工神经元实现

1. 数学表达

单个神经元的计算过程可分为以下步骤：

1）输入阶段：

• 接收n维输入向量X = [x₁, x₂, ..., xₙ]
• 每个输入xᵢ对应一个权重wᵢ

2）加权求和：

• 计算加权和z = w₁x₁ + w₂x₂ + ... + wₙxₙ + b
• 偏置项b的作用是调整神经元的激活阈值

3）激活输出：

• 应用激活函数y = f(z)
• 常用激活函数示例：
  • Sigmoid：f(z) = 1/(1+e⁻ᶻ)
  • ReLU：f(z) = max(0,z)
  • Tanh：f(z) = (eᶻ - e⁻ᶻ)/(eᶻ + e⁻ᶻ)

数学表达式中各参数含义： • xᵢ：第i个输入信号（如特征值或前一层的输出） • wᵢ：对应输入的连接权重（决定输入的重要性） • b：偏置项（调整神经元激活的难易程度） • f：非线性激活函数（引入非线性表达能力）

应用场景说明：

• 在图像识别中，xᵢ可能代表像素值
• 在自然语言处理中，xᵢ可能代表词向量维度
• 权重wᵢ通过训练过程自动学习得到

感知机（Perceptron）是神经网络发展史上第一个可学习的计算模型，由Frank Rosenblatt于1957年在康奈尔航空实验室提出。作为人工神经网络的雏形，感知机不仅开创了机器学习的新范式，更为现代深度学习的发展奠定了基础。

感知器是人工神经网络中最简单的形式，也是深度学习的基础组成部分。作为单层神经网络，感知器在机器学习发展史上具有里程碑式的意义。

感知器

一、感知器的基本概念

1. 数学模型

感知器的数学模型可以表示为：

y = f(∑(w_i * x_i) + b)

其中各参数详细说明：

• 输入特征(x_i)：表示感知器接收的第i个输入信号。例如在图像识别中，可以是像素值；在房价预测中，可以是房屋面积、卧室数量等特征。

• 权重(w_i)：每个输入特征对应的权重参数，决定了该特征对输出的影响程度。在训练过程中这些权重会被不断调整。

• 偏置项(b)：类似于线性函数中的截距，用于调整神经元的激活阈值。它允许我们移动决策边界而不依赖于输入。

• 激活函数(f)：通常为阶跃函数（原始感知器），其数学表达式为：

  f(z) = { 1, if z ≥ 0

  { 0, otherwise

  现代神经网络中常用其他激活函数如Sigmoid、ReLU等作为替代。

2. 工作原理

感知器的工作流程可分为以下几个步骤：

1. 输入接收：同时接收多个输入信号x₁, x₂,...,xn
2. 加权求和：计算各输入与对应权重的乘积之和 ∑(w_i * x_i)
3. 偏置处理：加上偏置项b，形成净输入 z = ∑(w_i * x_i) + b
4. 激活判断：通过激活函数f(z)产生二值输出(0或1)

这个过程模拟了生物神经元的工作方式：当"刺激"(加权和)超过某个阈值(由偏置控制)时，神经元就会被激活。例如，在垃圾邮件分类中，输入可以是邮件中的关键词频率，输出0表示正常邮件，1表示垃圾邮件。

感知器的结构与类型

1. 基本结构

感知器的基本结构包含三个主要组成部分：

1. 输入层：

   • 接收外部输入特征
   • 每个输入节点对应一个特征
   • 通常不进行任何计算处理

2. 权重和求和单元：

   • 存储权重参数(w₁,w₂,...,wn)
   • 执行加权求和计算 ∑(w_i * x_i)
   • 加上偏置项b

3. 激活函数：

   • 接收求和结果z
   • 应用非线性变换
   • 产生最终输出y

2. 激活函数类型

感知器可以使用多种激活函数：

1. 阶跃函数(原始感知器)：

   • 最早使用的激活函数
   • 输出仅为0或1
   • 缺点：不可微，不能用于梯度下降

2. Sigmoid函数：

   • 输出范围(0,1)
   • 表达式：σ(z) = 1/(1+e^{-z})
   • 优点：平滑可微
   • 常用于概率输出

3. ReLU函数(现代变种)：

   • 表达式：ReLU(z) = max(0,z)
   • 目前最常用的激活函数
   • 解决了梯度消失问题
   • 计算效率高

3. 单层与多层感知器

1. 单层感知器：

   • 仅包含输入层和输出层
   • 只能学习线性决策边界
   • 可以完美解决线性可分问题(如AND、OR逻辑运算)
   • 无法解决XOR等非线性可分问题
   • 典型应用：简单的线性分类任务

2. 多层感知器(MLP)：

   • 包含一个或多个隐藏层
   • 每层都有对应的权重和激活函数
   • 理论上可以逼近任何连续函数(万能逼近定理)
   • 能够解决复杂的非线性问题
   • 典型应用：图像识别、语音处理等复杂模式识别任务
   • 示例：一个简单的3层MLP结构：输入层(4个节点)→隐藏层(5个节点)→输出层(1个节点)

中间层的确立

输入层的节点数：与特征的维度匹配

输出层的节点数：与目标的维度匹配。

中间层的节点数：目前业界没有完善的理论来指导这个决策。一般是根据经验来设置。较好的方法就是预先设定几个可选值，通过切换这几个值来看整个模型的预测效果，选择效果最好的值作为最终选择。

损失函数

均方差损失（MSE）与交叉熵损失的理论解析

均方差损失（MSE）与交叉熵损失的理论解析

一、均方差损失（Mean Squared Error）

数学定义 • 基本形式：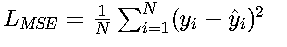

其中N为样本数量，y_i为真实值，ŷ_i为预测值。例如在房价预测中，若真实价格为300万，预测值为280万，则单个样本损失为(300-280)^2=400

• 矩阵形式：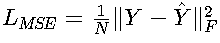

Frobenius范数在批量计算时更高效，特别适用于深度学习框架中的矩阵运算

概率解释 • 对应高斯分布的最大似然估计：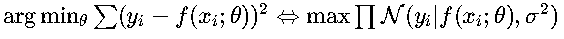

这意味着当数据噪声服从高斯分布时，MSE是最优的损失函数选择

• 噪声假设： 假设观测误差ε~N(0,σ^2)，且各样本噪声相互独立。这种假设在物理测量等场景中常见

梯度特性 • 单样本梯度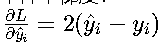： 梯度与误差成正比，在反向传播时提供线性更新信号

• Hessian矩阵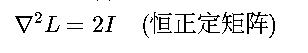： 严格凸性保证优化过程不会陷入局部最优

理论性质 • 凸性分析： 二次函数的凸性保证全局最优解存在，在凸优化问题中具有理论保证

• 利普希茨常数： 梯度满足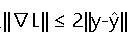，影响学习率的选择和收敛速度

• 异常值敏感度： 平方项使大误差被放大10倍，如10单位误差产生100损失，而1单位误差仅产生1损失

二、交叉熵损失（Cross-Entropy）

数学定义 • 二分类形式：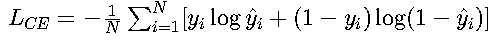

典型应用于逻辑回归，如肿瘤分类中y_i∈{0,1}表示恶性/良性

• 多分类形式：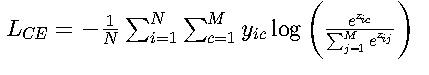

配合Softmax使用，适用于图像分类等任务（如MNIST手写数字识别）

信息论基础 • KL散度关系：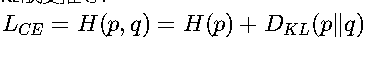

其中H(p)是真实分布的熵，D_KL衡量预测分布与真实分布的差异

• 似然估计等价： 等价于最大化伯努利分布的似然函数，在分类问题中具有统计合理性

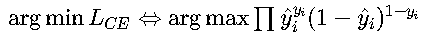
梯度特性 • Softmax梯度：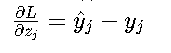

这种简洁形式使得反向传播计算效率极高

• 曲率分析： 半正定的Hessian矩阵在凸区域保证优化稳定性理论性质 • 极端惩罚： 当预测概率接近0而真实标签为1时，损失趋向无穷大，迫使模型做出明确判断

• 类别平衡： 可通过调整权重w解决样本不平衡问题，如在医学诊断中提高罕见病的权重

三、理论对比分析

特性	MSE	Cross-Entropy
​​输出空间​​	连续值（ℝ）	概率空间（[0,1]）
​​概率假设​​	高斯噪声	多项分布
​​梯度饱和性​​	线性梯度无饱和	极端概率时梯度饱和
​​最优预测​​	条件期望 E[y|x]	条件概率 P(y|x)
​​多分类扩展​​	需配合欧式距离	天然支持（Softmax）
​​异常值鲁棒性​​	低（平方放大）	高（对数抑制）

梯度下降法

一、梯度下降的数学基础

1. 一阶优化理论

梯度下降法建立在一阶优化理论的基础上，其核心思想是沿着目标函数负梯度方向迭代更新参数：

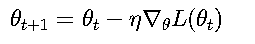
其中η为学习率(learning rate)，∇_θ L(θ_t)表示目标函数在θ_t处的梯度。收敛条件需满足Lipschitz连续性：

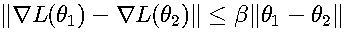
这一条件保证了梯度变化不会过于剧烈，使得算法能够稳定收敛。例如在逻辑回归中，交叉熵损失函数就满足此条件。

2. 泰勒展开解释

通过泰勒展开可以更深入理解梯度下降的数学本质。对目标函数进行二阶近似：

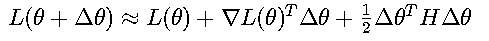
其中H是Hessian矩阵。由此可推导出最优步长：

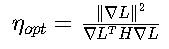
在实际应用中，由于计算Hessian矩阵代价高昂，通常使用固定学习率或自适应学习率策略。

二、基本算法形式

1. 批量梯度下降 (BGD)

批量梯度下降使用全部训练数据计算梯度：

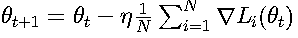
其收敛性可表示为：

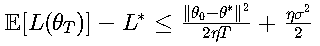
2. 随机梯度下降 (SGD)

随机梯度下降每次随机选取一个样本更新：

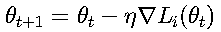
收敛速率为：

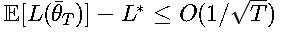
3. 小批量梯度下降 (Mini-batch GD)

折中方案使用小批量数据(batch)：

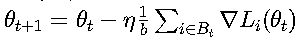
批次大小b影响梯度方差：

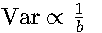
三、优化策略改进

1. 动量方法 (Momentum)

引入动量项加速收敛并减少震荡：

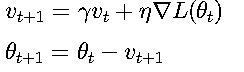
动量系数γ∈(0,1)模拟物理惯性，常见设置为0.9。

2. 自适应学习率方法

AdaGrad算法：

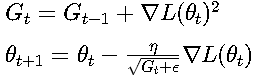
Adam算法结合动量和自适应学习率：

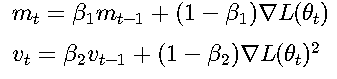
四、收敛性理论

1. 凸函数收敛

对于强凸函数：

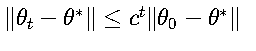
对于一般凸函数：

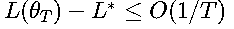
2. 非凸函数收敛

在非凸情况下：

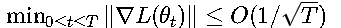
对于鞍点问题：

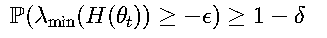
五、实现技术细节

1. 学习率调度

衰减策略：

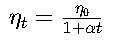
余弦退火：

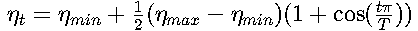
2. 梯度裁剪

控制梯度范数防止爆炸：

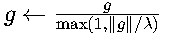
六、前沿发展

1. 二阶优化方法

拟牛顿法近似Hessian矩阵：

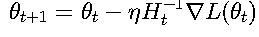
使用Fisher信息矩阵：

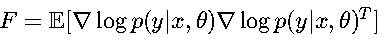
2. 分布式优化

参数服务器架构：

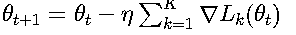
通信压缩技术：

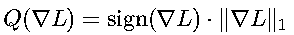
BP神经网络

BP（Back-propagation，反向传播）前向传播得到误差，反向传播调整误差，再前向传播，再反向传播一轮一轮得到最优解的。

BP神经网络反向传播理论精要

一、前向传播理论

1. 线性变换

神经网络第l层的第j个神经元的输入z_j^(l)通过以下线性变换得到：

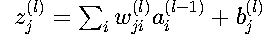
其中：

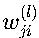• ：第l层第j个神经元与第l-1层第i个神经元的连接权重
  • 例如，在一个3层神经网络中，w_24^(2)表示第二层的第2个神经元与第一层第4个神经元的连接权重
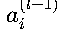• ：第l-1层第i个神经元的激活值
  • 对于输入层(l=1)，a_i^(0)即为网络输入x_i
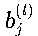• ：第l层第j个神经元的偏置项
  • 偏置项允许激活函数在输入为0时也能产生非零输出

2. 非线性激活

每个神经元的输出a_j^(l)通过激活函数g(z_j^(l))

计算：

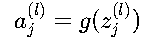
常用激活函数及其导数：

Sigmoid函数：

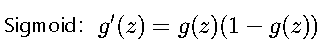
• 特点：将输入压缩到(0,1)区间
• 示例：当z=0时，g(0)=0.5，g'(0)=0.25

ReLU函数：

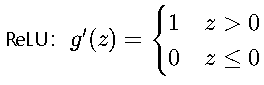
• 特点：计算简单，缓解梯度消失问题
• 应用场景：在深层网络中表现优异

二、损失函数构造

1. 均方差损失(MSE)

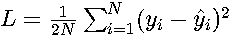
其中：

• N：样本数量
• y_i：第i个样本的真实值
• ŷ_i：第i个样本的预测值
• 1/2系数：方便求导时消去平方项的2

2. L2正则化项

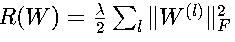
其中：

• λ：正则化系数，控制正则化强度
• ||W^(l)||_F：权重矩阵的Frobenius范数
• 作用：防止过拟合，使权重趋于较小值

3. 复合目标函数

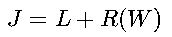
• 训练目标：最小化J
• 实际应用中可能还包括其他正则化项

三、反向传播理论

1. 输出层误差

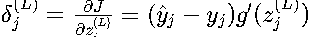
推导过程：

1. ∂J/∂ŷ_j = ŷ_j - y_j
2. ∂ŷ_j/∂z_j^(L) = g'(z_j^(L))
3. 根据链式法则相乘得到δ_j^(L)

2. 隐藏层误差传播

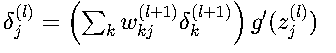
解释：

• ∑_k w_kj^(l+1) * δ_k^(l+1)：将后一层的误差反向传播到当前层
• g'(z_j^(l))：考虑当前层的非线性变换

3. 参数梯度计算

权重梯度：

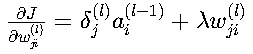
• 第一项：误差信号与前一层的激活值相乘
• 第二项：L2正则化带来的额外项

偏置梯度：

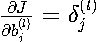
四、参数更新理论

1. 梯度下降规则

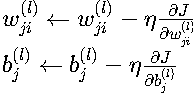
其中：

• η：学习率，控制更新步长
• 实际应用中可能使用改进的优化器(如Adam、RMSProp等)

2. 收敛条件

梯度范数阈值：

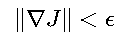
• ε：预设的极小正数
• 表示参数变化已足够小

最大迭代次数限制：

• 防止无限循环
• 常用值：1000-10000次迭代

五、理论特性分析

1. 链式法则本质

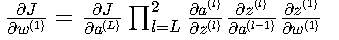
• 展示了误差从输出层到输入层的传播路径
• 解释了深层网络训练困难的原因

2. 梯度消失机理

当|g'(z)|<1时：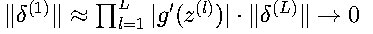

• 典型表现：使用Sigmoid激活的深层网络
• 解决方案：使用ReLU、残差连接等

3. 隐式正则化效应

梯度下降等价于：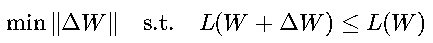

• 解释了为什么梯度下降倾向于找到平坦的最小值
• 与显式正则化(L1/L2)有协同作用