文章目录
-
- [一、平面点集 * n n n 维空间](#一、平面点集 * n n n 维空间)
-
- 1.平面点集
- [*2. n n n 维空间](#*2. n n n 维空间)
- 二、多元函数的概念
- 三、多元函数的极限
- 四、多元函数的连续性
一、平面点集 * n n n 维空间
1.平面点集
由平面解析几何知道,当在平面上引入了一个平面直角坐标系后,平面上的点 P P P 与有序二元实数组 ( x , y ) (x, y) (x,y) 之间就建立了一一对应。于是,我们常把有序实数组 ( x , y ) (x, y) (x,y) 与平面上的点 P P P 视作是等同的。这种建立了坐标系的平面称为坐标平面。二元有序实数组 ( x , y ) (x, y) (x,y) 的全体,即 R 2 = R × R = { ( x , y ) ∣ x , y ∈ R } \mathbb{R}^2 = \mathbb{R} \times \mathbb{R} = \{ (x, y) | x, y \in \mathbb{R} \} R2=R×R={(x,y)∣x,y∈R} 就表示坐标平面。
坐标平面上具有某种性质 P P P 的点的集合,称为平面点集,记作
E = { ( x , y ) ∣ ( x , y ) 具有性质 P } . E = \{ (x, y) | (x, y)具有性质P \}. E={(x,y)∣(x,y)具有性质P}.
例如,平面上以原点为中心、 r r r 为半径的圆内所有的点的集合是
C = { ( x , y ) ∣ x 2 + y 2 < r } . C = \{ (x, y)|x^2 + y^2 < r \}. C={(x,y)∣x2+y2<r}.
如果以点 P P P 表示 ( x , y ) (x, y) (x,y) , ∣ O P ∣ |OP| ∣OP∣ 表示点 P P P 到原点 O O O 的距离,那么集合 C C C 也可以表成
C = { P ∣ ∣ O P ∣ < r } C = \{ P | |OP| < r \} C={P∣∣OP∣<r}
现在引入 R 2 \mathbb{R}^2 R2 中邻域的概念。
设 P 0 ( x 0 , y 0 ) P_0 (x_0, y_0) P0(x0,y0) 是 x O y xOy xOy 平面上的一个点, δ \delta δ 是某一正数。与点 P 0 ( x 0 , y 0 ) P_0 (x_0, y_0) P0(x0,y0) 距离小于 δ \delta δ 的点 P ( x , y ) P(x, y) P(x,y) 的全体,称为点 P 0 P_0 P0 的 δ \delta δ 邻域 ,记作 U ( P 0 , δ ) U(P_0, \delta) U(P0,δ) ,即
U ( P 0 , δ ) = { P ∣ ∣ P P 0 ∣ < δ } , U(P_0, \delta) = \{ P | |PP_0| < \delta \}, U(P0,δ)={P∣∣PP0∣<δ},
也就是
U ( P 0 , δ ) = { ( x , y ) ∣ ( x − x 0 ) 2 + ( y − y 0 ) 2 < δ } . U(P_0, \delta) = \{ (x, y) | \sqrt{(x - x_0)^2 + (y - y_0)^2} < \delta \}. U(P0,δ)={(x,y)∣(x−x0)2+(y−y0)2 <δ}.
点 P 0 P_0 P0 的去心 δ \delta δ 邻域,记作 U ˚ ( P 0 , δ ) \mathring{U} (P_0, \delta) U˚(P0,δ) ,即
U ˚ ( P 0 , δ ) = { P ∣ 0 < ∣ P P 0 ∣ < δ } \mathring{U} (P_0, \delta) = \{ P | 0 < |PP_0| < \delta \} U˚(P0,δ)={P∣0<∣PP0∣<δ}
在几何上, U ( P 0 , δ ) U(P_0, \delta) U(P0,δ) 就是 x O y xOy xOy 平面上以点 P 0 ( x 0 , y 0 ) P_0(x_0, y_0) P0(x0,y0) 为中心、 δ > 0 \delta > 0 δ>0 为半径的圆内部的点 P ( x , y ) P(x, y) P(x,y) 的全体。
如果不需要强调领域的半径 δ \delta δ ,则用 U ( P 0 ) U(P_0) U(P0) 表示点 P 0 P_0 P0 的某个邻域,点 P 0 P_0 P0 的去心邻域记作 U ˚ ( P 0 ) \mathring{U}(P_0) U˚(P0) 。
利用邻域来描述点和点集之间的关系。
任意一点 P ∈ R 2 P \in \mathbb{R}^2 P∈R2 与任意一个点集 E ⊂ R 2 E \subset \mathbb{R}^2 E⊂R2 之间必有一下三种关系中的一种:
(1)内点 :如果存在点 P P P 的某个邻域 U ( P ) U(P) U(P) ,使得 U ( P ) ⊂ E U(P) \subset E U(P)⊂E ,那么称 P P P 为 E E E 的内点(如图9-1中, P 1 P_1 P1 为 E E E 的内点);
(2)外点 :如果存在点 P P P 的某个邻域 U ( P ) U(P) U(P) ,使得 U ( P ) ∩ E = ∅ U(P) \cap E = \varnothing U(P)∩E=∅ ,那么称 P P P 为 E E E 的外点(如图9-1中, P 2 P_2 P2 为 E E E 的外点);
(3)边界点 :如果点 P P P 的任一邻域内既含有属于 E E E 的点,又含有不属于 E E E 的点,那么称 P P P 为 E E E 的边界点(如图9-1中, P 3 P_3 P3 为 E E E 的边界点)。
E E E 的边界点的全体,称为 E E E 的 边界 ,记作 ∂ E \partial E ∂E 。
E E E 的内点必属于 E E E ; E E E 的外点必定不属于 E E E ;而 E E E 的边界点可能属于 E E E ,也可能不属于 E E E 。
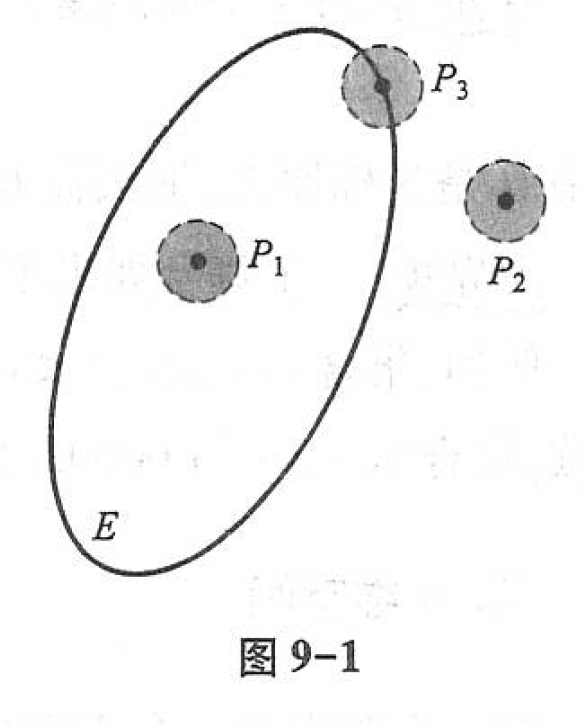
任意一点 P P P 与一个点集 E E E 之间除了上述三种关系之外,还有另外一种关系,这就是聚点。
聚点 :如果对于任意给定的 δ > 0 \delta > 0 δ>0 ,点 P P P 的去心邻域 U ˚ ( P , δ ) \mathring{U}(P, \delta) U˚(P,δ) 内总有 E E E 中的点,那么称 P P P 是 E E E 的 聚点 。
由聚点的定义可知,点集 E E E 的聚点 P P P 本身,可以属于 E E E ,也可以不属于 E E E 。
例如,设平面点集
E = { ( x , y ) ∣ 1 < x 2 + y 2 ⩽ 2 } . E = \{ (x, y) | 1 < x^2 + y^2 \leqslant 2 \}. E={(x,y)∣1<x2+y2⩽2}.
满足 1 < x 2 + y 2 < 2 1 < x^2 + y^2 < 2 1<x2+y2<2 的一切点 ( x , y ) (x, y) (x,y) 都是 E E E 的内点;满足 x 2 + y 2 = 1 x^2 + y^2 = 1 x2+y2=1 的一切点 ( x , y ) (x, y) (x,y) 都是 E E E 的边界点,它们都不属于 E E E ;满足 x 2 + y 2 = 2 x^2 + y^2 = 2 x2+y2=2 的一切点 ( x , y ) (x, y) (x,y) 也是 E E E 的边界点,它们都属于 E E E ;点集 E E E 以及它的边界 ∂ E \partial E ∂E 上的一切点都是 E E E 的聚点。
根据点集所属点的特征,再来定义一些重要的平面点集。
开集 :如果点集 E E E 的点都是 E E E 的内点,那么称 E E E 为开集。
闭集 :如果点集 E E E 的边界 ∂ E ⊂ E \partial E \subset E ∂E⊂E ,那么称 E E E 为闭集。
例如,集合 { ( x , y ) ∣ 1 < x 2 + y 2 < 2 } \{ (x, y) | 1 < x^2 + y^2 < 2 \} {(x,y)∣1<x2+y2<2} 是开集;集合 { ( x , y ) ∣ 1 ⩽ x 2 + y 2 ⩽ 2 } \{ (x, y) | 1 \leqslant x^2 + y^2 \leqslant 2 \} {(x,y)∣1⩽x2+y2⩽2} 是闭集;而集合 { ( x , y ) ∣ 1 < x 2 + y 2 ⩽ 2 } \{ (x, y) | 1 < x^2 + y^2 \leqslant 2 \} {(x,y)∣1<x2+y2⩽2} 既非开集,也非闭集。
连通集 :如果点集 E E E 内任何两点,都可用折线连接起来,且该折线上的点都属于 E E E ,那么称 E E E 为连通集。
区域 (或 开区域):连通的开集称为区域或开区域。
闭区域 :开区域连同它的边界一起所构成的点集称为闭区域。
例如,集合 { ( x , y ) ∣ 1 < x 2 + y 2 < 2 } \{ (x, y) | 1 < x^2 + y^2 < 2 \} {(x,y)∣1<x2+y2<2} 是区域,而集合 { ( x , y ) ∣ 1 ⩽ x 2 + y 2 ⩽ 2 } \{ (x, y) | 1 \leqslant x^2 + y^2 \leqslant 2 \} {(x,y)∣1⩽x2+y2⩽2} 是闭区域。
有界集 :对于平面点集 E E E ,如果存在某一正数 r r r ,使得
E ⊂ U ( O , r ) E \subset U(O, r) E⊂U(O,r)
其中 O O O 是坐标原点,那么称 E E E 为有界集。
无界集 :一个集合如果不是有界集,就成这个集合为无界集。
例如,集合 { ( x , y ) ∣ 1 ⩽ x 2 + y 2 ⩽ 2 } \{ (x, y) | 1 \leqslant x^2 + y^2 \leqslant 2 \} {(x,y)∣1⩽x2+y2⩽2} 是有界闭区域,集合 { ( x , y ) ∣ x + y > 0 } \{ (x, y) | x + y > 0 \} {(x,y)∣x+y>0} 是无界开区域,集合 { ( x , y ) ∣ x + y ⩾ 0 } \{ (x, y) | x + y \geqslant 0 \} {(x,y)∣x+y⩾0} 是无界闭区域。
*2. n n n 维空间
设 n n n 为取定的一个正整数,我们用 R n \mathbb{R}^n Rn 表示 n n n 元有序实数组 ( x 1 , x 2 , ⋯ , x n ) (x_1, x_2, \cdots, x_n) (x1,x2,⋯,xn) 的全体所构成的集合,即
R n = R × R × ⋯ × R { ( x 1 , x 2 , ⋯ , x n ) ∣ x i ∈ R , i = 1 , 2 , ⋯ , n } . \mathbb{R}^n = \mathbb{R} \times \mathbb{R} \times \cdots \times \mathbb{R} \{ (x_1, x_2, \cdots, x_n) | x_i \in \mathbb{R}, i = 1, 2, \cdots, n \}. Rn=R×R×⋯×R{(x1,x2,⋯,xn)∣xi∈R,i=1,2,⋯,n}.
R n \mathbb{R}^n Rn 中的元素 ( x 1 , x 2 , ⋯ , x n ) (x_1, x_2, \cdots, x_n) (x1,x2,⋯,xn) 有时也用单个字母 x \boldsymbol{x} x 来表示,即 x = ( x 1 , x 2 , ⋯ , x n ) \boldsymbol{x} = (x_1, x_2, \cdots, x_n) x=(x1,x2,⋯,xn) .当所有的 x i ( i = 1 , 2 , ⋯ , n ) x_i(i = 1, 2, \cdots, n) xi(i=1,2,⋯,n) 都为零时,称这样的元素为 R 2 \mathbb{R}^2 R2 中的零元,记为 0 \boldsymbol{0} 0 或 O O O 。在解析几何中,通过直角坐标系, R 2 \mathbb{R}^2 R2 (或 R 3 \mathbb{R}^3 R3)中的元素分别与平面(或空间)中的点或向量建立一一对应,因而 R n \mathbb{R}^n Rn 中的元素 x = ( x 1 , x 2 , ⋯ , x n ) \boldsymbol{x} = (x_1, x_2, \cdots, x_n) x=(x1,x2,⋯,xn) 也称为 R n \mathbb{R}^n Rn 中的一个点或一个 n n n 维向量, x i x_i xi 称为点 x x x 的第 i i i 个坐标或 n n n 维向量 x \boldsymbol{x} x 的第 i i i 个分量。特别地, R 2 \mathbb{R}^2 R2 中的零元 0 \boldsymbol{0} 0 称为 R n \mathbb{R}^n Rn 中的坐标原点或 n n n 维零向量。
为了在集合 R n \mathbb{R}^n Rn 中的元素之间建立联系,在 R n \mathbb{R}^n Rn 中定义线性运算如下:
设 x = ( x 1 , x 2 , ⋯ , x n ) \boldsymbol{x} = (x_1, x_2, \cdots, x_n) x=(x1,x2,⋯,xn) , y = ( y 1 , y 2 , ⋯ , y n ) \boldsymbol{y} = (y_1, y_2, \cdots, y_n) y=(y1,y2,⋯,yn) 为 R n \mathbb{R}^n Rn 中的任意两个元素, λ ∈ R \lambda \in \mathbb{R} λ∈R ,规定
x + y = ( x 1 + y 1 , x 2 + y 2 , ⋯ , x n + y n ) λ x = ( λ x 1 , λ x 2 , ⋯ , λ x n ) . \boldsymbol{x} + \boldsymbol{y} = (x_1 + y_1, x_2 + y_2, \cdots, x_n + y_n) \\ \lambda \boldsymbol{x} = (\lambda x_1, \lambda x_2, \cdots, \lambda x_n). x+y=(x1+y1,x2+y2,⋯,xn+yn)λx=(λx1,λx2,⋯,λxn).
这样定义了线性运算的集合 R n \mathbb{R}^n Rn 称为 n n n 维空间。
R n \mathbb{R}^n Rn 中的点 x = ( x 1 , x 2 , ⋯ , x n ) \boldsymbol{x} = (x_1, x_2, \cdots, x_n) x=(x1,x2,⋯,xn) 和点 y = ( y 1 , y 2 , ⋯ , y n ) \boldsymbol{y} = (y_1, y_2, \cdots, y_n) y=(y1,y2,⋯,yn) 间的距离,记作 ρ ( x , y ) \rho(\boldsymbol{x}, \boldsymbol{y}) ρ(x,y) ,规定
ρ ( x , y ) = ( x 1 − y 1 ) 2 + ( x 2 − y 2 ) 2 + ⋯ + ( x n − y n ) 2 . \rho (\boldsymbol{x}, \boldsymbol{y}) = \sqrt{(x_1 - y_1)^2 + (x_2 - y_2)^2 + \cdots + (x_n - y_n)^2}. ρ(x,y)=(x1−y1)2+(x2−y2)2+⋯+(xn−yn)2 .
显然, n = 1 , 2 , 3 n = 1, 2, 3 n=1,2,3 时,上述规定与数轴上、直角坐标系下平面及空间中两点间的距离一致。
R n \mathbb{R}^n Rn 中元素 x = ( x 1 , x 2 , ⋯ , x n ) \boldsymbol{x} = (x_1, x_2, \cdots, x_n) x=(x1,x2,⋯,xn) 与零元 0 \boldsymbol{0} 0 之间的距离 ρ ( x , 0 ) \rho (\boldsymbol{x}, \boldsymbol{0}) ρ(x,0) 记作 ∥ x ∥ \| \boldsymbol{x} \| ∥x∥ (在 R 1 , R 2 , R 3 \mathbb{R}^1, \mathbb{R}^2, \mathbb{R}^3 R1,R2,R3 中,通常将 ∥ x ∥ \| \boldsymbol{x} \| ∥x∥ 记作 ∣ x ∣ |\boldsymbol{x}| ∣x∣),即
∥ x ∥ = x 1 2 + x 2 2 + ⋯ + x n 2 . \| \boldsymbol{x} \| = \sqrt{x_1^2 + x_2^2 + \cdots + x_n^2}. ∥x∥=x12+x22+⋯+xn2 .
采用这一记号,结合向量的线性运算,便得
∥ x − y ∥ = ( x 1 − y 1 ) 2 + ( x 2 − y 2 ) 2 + ⋯ + ( x n − y n ) 2 = ρ ( x , y ) \| \boldsymbol{x} - \boldsymbol{y} \| = \sqrt{(x_1 - y_1)^2 + (x_2 - y_2)^2 + \cdots + (x_n - y_n)^2} = \rho (\boldsymbol{x}, \boldsymbol{y}) ∥x−y∥=(x1−y1)2+(x2−y2)2+⋯+(xn−yn)2 =ρ(x,y)
在 n n n 维空间 R n \mathbb{R}^n Rn 中定义了距离以后,就可以定义 R n \mathbb{R}^n Rn 的变元的极限:
设 x = ( x ! , x 2 , ⋯ , x n ) , a = ( a 1 , a 2 , ⋯ , a n ) ∈ R n \boldsymbol{x} = (x_!, x_2, \cdots, x_n) , \boldsymbol{a} = (a_1, a_2, \cdots, a_n) \in \mathbb{R}^n x=(x!,x2,⋯,xn),a=(a1,a2,⋯,an)∈Rn 。如果
∥ x − a ∥ → 0 , \| \boldsymbol{x} - \boldsymbol{a} \| \to 0, ∥x−a∥→0,
那么称变元 x \boldsymbol{x} x 在 R n \mathbb{R}^n Rn 中趋于固定元 a \boldsymbol{a} a ,记作 x → a \boldsymbol{x} \to \boldsymbol{a} x→a 。
显然,
x → a ⇔ x 1 → a 1 , x 2 → a 2 , ⋯ , x n → a n . \boldsymbol{x} \to \boldsymbol{a} \Leftrightarrow x_1 \to a_1, x_2 \to a_2, \cdots, x_n \to a_n . x→a⇔x1→a1,x2→a2,⋯,xn→an.
在 R 2 \mathbb{R}^2 R2 中引入线性运算和距离,使得有关平面点集的一些列概念,可以方便地引入到 n ( n ⩾ 3 ) n(n \geqslant 3) n(n⩾3) 维空间中来。例如,
设 a = ( a 1 , a 2 , ⋯ , a n ) ∈ R n \boldsymbol{a} = (a_1, a_2, \cdots, a_n) \in \mathbb{R}^n a=(a1,a2,⋯,an)∈Rn , δ \delta δ 是某一正数,则 n n n 维空间内的点集
U ( a , δ ) = { x ∣ x ∈ R 2 , ρ ( x , a ) < δ } U(\boldsymbol{a}, \delta) = \{ \boldsymbol{x} | \boldsymbol{x} \in \mathbb{R}^2, \rho(\boldsymbol{x}, \boldsymbol{a}) < \delta \} U(a,δ)={x∣x∈R2,ρ(x,a)<δ}
就定义为 R n \mathbb{R}^n Rn 中点 a \boldsymbol{a} a 的 δ \delta δ 邻域。以邻域为基础,可以定义点集的内点、外点、边界点和聚点以及开集、闭集、区域等一系列概念。
二、多元函数的概念
定义1 设 D D D 是 R 2 \mathbb{R}^2 R2 上的一个非空子集,称映射 f : D → R f:D \to \mathbb{R} f:D→R 为定义在 D D D 上的 二元函数 ,通常记为
z = f ( x , y ) , ( x , y ) ∈ D z = f(x, y), \quad (x, y) \in D z=f(x,y),(x,y)∈D
或
z = f ( P ) , P ∈ D , z = f(P), \quad P \in D, z=f(P),P∈D,
其中点集 D D D 称为该函数的 定义域 , x x x 和 y y y 称为 自变量 , z z z 称为 因变量 。
上述定义中,与自变量 x {x} x 和 y {y} y 的一对值(即二元有序实数组) ( x , y ) {(x, y)} (x,y) 相对应的因变量 z {z} z 的值,也称为 f {f} f 在点 ( x , y ) {(x, y)} (x,y) 处的函数值,记作 f ( x , y ) {f(x, y)} f(x,y) ,即 z = f ( x , y ) {z=f(x, y)} z=f(x,y) .函数值 f ( x , y ) {f(x, y)} f(x,y) 的全体所构成的集合称为函数 f {f} f 的值域,记作 f ( D ) {f(D)} f(D) ,即
f ( D ) = { z ∣ z = f ( x , y ) , ( x , y ) ∈ D } . f(D)=\{z | z=f(x, y),(x, y) \in D\} . f(D)={z∣z=f(x,y),(x,y)∈D}.
与一元函数的情形相仿,记号 f {f} f 与 f ( x , y ) {f(x, y)} f(x,y) 的意义是有区别的,但习惯上常用记号 " f ( x , y ) , ( x , y ) ∈ D {f(x, y),(x, y) \in D} f(x,y),(x,y)∈D"或" z = f ( x , y ) , ( x , y ) ∈ D {z=f(x, y),(x, y) \in D} z=f(x,y),(x,y)∈D"来表示 D {D} D 上的二元函数 f {f} f .表示二元函数的记号 f {f} f 也是可以任意选取的,例如也可以记为 z = φ ( x , y ) , z = z ( x , y ) {z=\varphi(x, y), z=z(x, y)} z=φ(x,y),z=z(x,y) 等.
类似地,可以定义三元函数 u = f ( x , y , z ) , ( x , y , z ) ∈ D {u=f(x, y, z),(x, y, z) \in D} u=f(x,y,z),(x,y,z)∈D 以及三元以上的函数.一般地,把定义 1 中的平面点集 D {D} D 换成 n {n} n 维空间 R n {\mathbb{R}^{n}} Rn 内的点集 D {D} D ,映射 f : D → R {f: D \rightarrow \mathbb{R}} f:D→R 就称为定义在 D {D} D 上的 n {n} n 元函数,通常记为
u = f ( x 1 , x 2 , ⋯ , x n ) , ( x 1 , x 2 , ⋯ , x n ) ∈ D u=f\left(x_{1}, x_{2}, \cdots, x_{n}\right), \left(x_{1}, x_{2}, \cdots, x_{n}\right) \in D u=f(x1,x2,⋯,xn),(x1,x2,⋯,xn)∈D
或简记为
u = f ( x ) , x = ( x 1 , x 2 , ⋯ , x n ) ∈ D u=f(x), x=\left(x_{1}, x_{2}, \cdots, x_{n}\right) \in D u=f(x),x=(x1,x2,⋯,xn)∈D
也可记为
u = f ( P ) , P ( x 1 , x 2 , ⋯ , x n ) ∈ D . u = f(P), \quad P(x_1, x_2, \cdots, x_n) \in D. u=f(P),P(x1,x2,⋯,xn)∈D.
当 n = 2 {n=2} n=2 或 n = 3 {n=3} n=3 时,习惯上将点 ( x 1 , x 2 ) {\left(x_{1}, x_{2}\right)} (x1,x2) 与点 ( x 1 , x 2 , x 3 ) {\left(x_{1}, x_{2}, x_{3}\right)} (x1,x2,x3) 分别写成 ( x , y ) {(x, y)} (x,y) 与 ( x , y , z ) {(x, y, z)} (x,y,z) .这时,若用字母表示 R 2 {\mathbb{R}^{2}} R2 或 R 3 {\mathbb{R}^{3}} R3 中的点,即写成 P ( x , y ) {P(x, y)} P(x,y) 或 M ( x , y , z ) {M(x, y, z)} M(x,y,z) ,则相应的二元函数及三元函数也可简记为 z = f ( P ) {z=f(P)} z=f(P) 及 u = f ( M ) {u=f(M)} u=f(M) .
当 n = 1 {n=1} n=1 时, n {n} n 元函数就是一元函数;当 n ⩾ 2 {n \geqslant 2} n⩾2 时, n {n} n 元函数统称为多元函数.
关于多元函数的定义域,与一元函数相类似,我们作如下约定:在一般地讨论用算式表达的多元函数 u = f ( x ) {u=f(x)} u=f(x) 时,就以使这个算式有意义的变元 x {x} x 的值所组成的点集为这个 多元函数的自然定义域 。因而,对这类函数,它的定义域不再特别标出。例如,函数 z = ln ( x + y ) {z=\ln (x+y)} z=ln(x+y) 的定义域为
{ ( x , y ) ∣ x + y > 0 } \{(x, y) | x+y>0\} {(x,y)∣x+y>0}
(图 9-2),这是一个无界开区域.

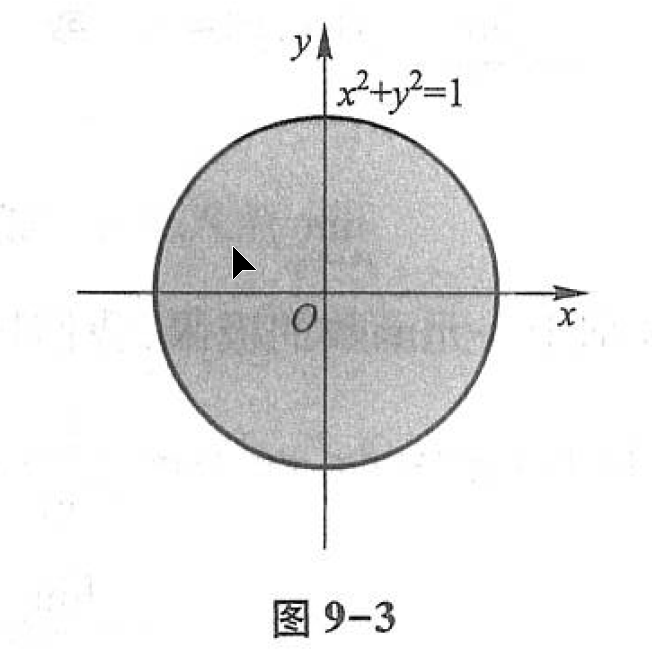
又如,函数 z = arcsin ( x 2 + y 2 ) {z=\arcsin \left(x^{2}+y^{2}\right)} z=arcsin(x2+y2) 的定义域为
{ ( x , y ) ∣ x 2 + y 2 ⩽ 1 } \left\{(x, y) | x^{2}+y^{2} \leqslant 1\right\} {(x,y)∣x2+y2⩽1}
(图9-3),这是一个有界闭区域.
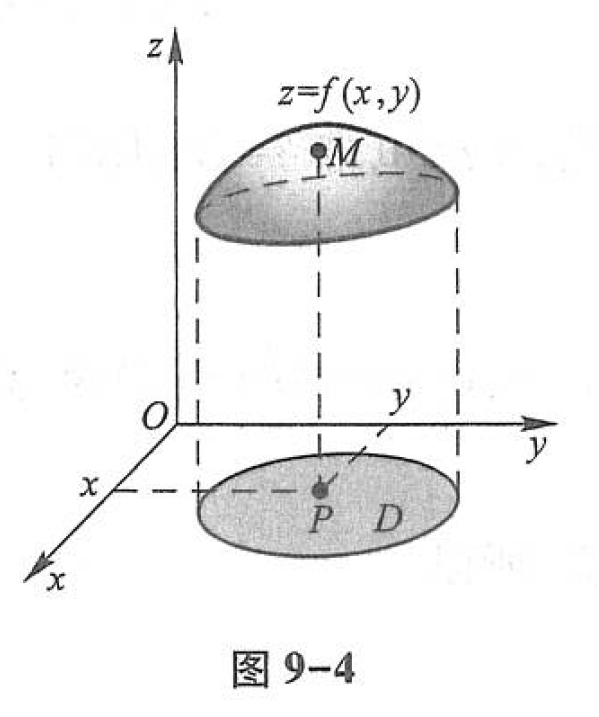
设函数 z=f(x, y) 的定义域为 D D D .对于任意取定的点 P ( x , y ) ∈ D P(x, y) \in D P(x,y)∈D ,对应的函数值为 z=f(x, y) .这样,以 x x x 为横坐标、 y y y 为纵坐标和 z=f(x, y) 为竖坐标在空间就确定一点 M ( x , y , z ) M(x, y, z) M(x,y,z) .当 ( x , y ) (x, y) (x,y) 遍取 D D D上的一切点时,得到一个空间点集
{ ( x , y , z ) ∣ z = f ( x , y ) , ( x , y ) ∈ D } , \{(x, y, z) \mid z=f(x, y),(x, y) \in D\}, {(x,y,z)∣z=f(x,y),(x,y)∈D},
这个点集称为 二元函数 z=f(x, y) 的图形 (图9-4).通常我们也说二元函数的图形是一张曲面.
例如,由空间解析几何知道,线性函数 z = a x + b y + c z=a x+b y+c z=ax+by+c的图形是一张平面,而函数 z = x 2 + y 2 z=x^{2}+y^{2} z=x2+y2 的图形是旋转抛物面.
三、多元函数的极限
先讨论二元函数 z = f ( x , y ) z=f(x, y) z=f(x,y) 当 ( x , y ) → ( x 0 , y 0 ) (x, y) \rightarrow\left(x_{0}, y_{0}\right) (x,y)→(x0,y0) ,即 P ( x , y ) → P 0 ( x 0 , y 0 ) P(x, y) \rightarrow P_{0}\left(x_{0}, y_{0}\right) P(x,y)→P0(x0,y0) 时的极限.
这里 P → P 0 P \rightarrow P_{0} P→P0 表示点 P P P 以任何方式趋于点 P 0 P_{0} P0 ,也就是点 P P P 与点 P 0 P_{0} P0 间的距离趋于零,即
∣ P P 0 ∣ = ( x − x 0 ) 2 + ( y − y 0 ) 2 → 0. \left|P P_{0}\right|=\sqrt{\left(x-x_{0}\right)^{2}+\left(y-y_{0}\right)^{2}} \rightarrow 0 . ∣PP0∣=(x−x0)2+(y−y0)2 →0.
与一元函数的极限概念类似,如果在 P ( x , y ) → P 0 ( x 0 , y 0 ) P(x, y) \rightarrow P_{0}\left(x_{0}, y_{0}\right) P(x,y)→P0(x0,y0) 的过程中,对应的函数值 f(x, y) 无限接近于一个确定的常数 A A A ,那么就说 A A A 是函数 f(x, y) 当 ( x , y ) → ( x 0 , y 0 ) (x, y) \rightarrow \left(x_{0}, y_{0}\right) (x,y)→(x0,y0) 时的极限.下面用" ε − δ \varepsilon-\delta ε−δ"语言描述这个极限概念.
定义 2 设二元函数 f ( P ) = f ( x , y ) f(P)=f(x, y) f(P)=f(x,y) 的定义域为 D , P 0 ( x 0 , y 0 ) D, P_{0}\left(x_{0}, y_{0}\right) D,P0(x0,y0) 是 D D D 的聚点.如果存在常数 A A A ,对于任意给定的正数 ε \varepsilon ε ,总存在正数 δ \delta δ ,使得当点 P ( x , y ) ∈ D ∩ U ∘ ( P 0 , δ ) P(x, y) \in D \cap \stackrel{\circ}{U}\left(P_{0}, \delta\right) P(x,y)∈D∩U∘(P0,δ) 时,都有
∣ f ( P ) − A ∣ = ∣ f ( x , y ) − A ∣ < ε |f(P)-A|=|f(x, y)-A|<\varepsilon ∣f(P)−A∣=∣f(x,y)−A∣<ε
成立,那么就称常数 A A A 为函数 f ( x , y ) f(x, y) f(x,y) 当 ( x , y ) → ( x 0 , y 0 ) (x, y) \rightarrow\left(x_{0}, y_{0}\right) (x,y)→(x0,y0) 时的极限,记作
lim ( x , y ) → ( x 0 , y 0 ) f ( x , y ) = A 或 f ( x , y ) → A ( ( x , y ) → ( x 0 , y 0 ) ) , \lim {(x, y) \rightarrow\left(x{0}, y_{0}\right)} f(x, y)=A \quad 或 \quad f(x, y) \rightarrow A\left((x, y) \rightarrow\left(x_{0}, y_{0}\right)\right) , (x,y)→(x0,y0)limf(x,y)=A或f(x,y)→A((x,y)→(x0,y0)),
也记作
lim P → P 0 f ( P ) = A 或 f ( P ) → A ( P → P 0 ) . \lim {P \rightarrow P{0}} f(P)=A \quad 或 \quad f(P) \rightarrow A\left(P \rightarrow P_{0}\right) . P→P0limf(P)=A或f(P)→A(P→P0).
为了区别于一元函数的极限,我们把二元函数的极限叫做 二重极限 。
必须注意,所谓二重极限存在,是指 P ( x , y ) P(x, y) P(x,y) 以任何方式趋于 P 0 ( x 0 , y 0 ) P_{0}\left(x_{0}, y_{0}\right) P0(x0,y0) 时, f(x, y) 都无限接近于 A A A 。因此,如果 P ( x , y ) P(x, y) P(x,y) 以某一特殊方式,例如沿着一条定直线或定曲线趋于 P 0 ( x 0 , y 0 ) P_{0}\left(x_{0}, y_{0}\right) P0(x0,y0) 时,即使 f(x, y) 无限接近于某一确定值,我们还不能由此断定函数的极限存在.但是反过来,如果当 P ( x , y ) P(x, y) P(x,y) 以不同的方式趋于 P 0 ( x 0 , y 0 ) P_{0}\left(x_{0}, y_{0}\right) P0(x0,y0) 时, f(x, y) 趋于不同的值,那么就可以断定这函数的极限不存在.
以上关于二元函数的极限概念,可相应地推广到 n n n 元函数 u = f ( P ) u=f(P) u=f(P) ,即 u = f ( x 1 u=f\left(x_{1}\right. u=f(x1 , x 2 , ⋯ , x n ) \left.x_{2}, \cdots, x_{n}\right) x2,⋯,xn) 上去.
关于多元函数的极限运算,有与一元函数类似的运算法则.
四、多元函数的连续性
定义 3 设二元函数 f ( P ) = f ( x , y ) f(P)=f(x, y) f(P)=f(x,y) 的定义域为 D , P 0 ( x 0 , y 0 ) D, P_{0}\left(x_{0}, y_{0}\right) D,P0(x0,y0) 为 D D D 的聚点,且 P 0 ∈ D P_{0} \in D P0∈D.如果
lim ( x , y ) → ( x 0 , y 0 ) f ( x , y ) = f ( x 0 , y 0 ) , \lim {(x, y) \rightarrow\left(x{0}, y_{0}\right)} f(x, y)=f\left(x_{0}, y_{0}\right), (x,y)→(x0,y0)limf(x,y)=f(x0,y0),
那么称函数 f(x, y) 在点 P 0 ( x 0 , y 0 ) P_{0}\left(x_{0}, y_{0}\right) P0(x0,y0) 连续.
设函数 f(x, y) 在 D D D 上有定义, D D D 内的每一点都是函数定义域的聚点。如果函数 f(x, y) 在 D D D 的每一点都连续,那么就称函数 f(x, y) 在 D D D 上连续,或者称 f(x, y) 是 D D D上的 连续函数 .
以上关于二元函数的连续性概念,可相应地推广到 n n n 元函数 f ( P ) f(P) f(P) 上去.
定义 4 设函数 f(x, y) 的定义域为 D , P 0 ( x 0 , y 0 ) D, P_{0}\left(x_{0}, y_{0}\right) D,P0(x0,y0) 是 D D D 的聚点.如果函数 f(x, y) 在点 P 0 ( x 0 , y 0 ) P_{0}\left(x_{0}, y_{0}\right) P0(x0,y0) 不连续,那么称 P 0 ( x 0 , y 0 ) P_{0}\left(x_{0}, y_{0}\right) P0(x0,y0) 为函数 f(x, y) 的间断点.
一切多元初等函数在其定义区域内是连续的。所谓 定义区域 是指包含在定义域内的区域或闭区域。
由多元初等函数的连续性,如果要求它在点 P 0 P_0 P0 处的极限,而该点又在此函数的定义区域内,那么此极限值就是函数在该点的函数值,即
lim P → P 0 f ( P ) = f ( P 0 ) . \lim \limits_{P \to P_0} f(P) = f(P_0). P→P0limf(P)=f(P0).
在有界闭区域上连续的多元函数具有如下性质:
性质1(有界性与最大值最小值定理) 在有界闭区域 D D D 上的多元连续函数,必定在 D D D 上有界,且能取得它的最大值和最小值.
性质1就是说,若 f ( P ) f(P) f(P) 在有界闭区域 D D D 上连续,则必定存在常数 M > 0 M>0 M>0 ,使得对一切 P ∈ D P \in D P∈D ,有 ∣ f ( P ) ∣ ⩽ M |f(P)| \leqslant M ∣f(P)∣⩽M ;且存在 P 1 , P 2 ∈ D P_{1}, P_{2} \in D P1,P2∈D ,使得
f ( P 1 ) = max { f ( P ) ∣ P ∈ D } , f ( P 2 ) = min { f ( P ) ∣ P ∈ D } . f\left(P_{1}\right)=\max \{f(P) \mid P \in D\}, \quad f\left(P_{2}\right)=\min \{f(P) \mid P \in D\} . f(P1)=max{f(P)∣P∈D},f(P2)=min{f(P)∣P∈D}.
性质2(介值定理) 在有界闭区域 D D D 上的多元连续函数必取得介于最大值和最小值之间的任何值.
*性质3(一致连续性定理) 在有界闭区域 D D D 上的多元连续函数必定在 D D D 上 一致连续 .
性质3就是说,若 f ( P ) f(P) f(P) 在有界闭区域 D D D 上连续,则对于任意给定的正数 ε \varepsilon ε ,总存在正数 δ \delta δ ,使得对于 D D D 上的任意两点 P 1 , P 2 P_{1}, P_{2} P1,P2 ,只要当 ∣ P 1 P 2 ∣ < δ \left|P_{1} P_{2}\right|<\delta ∣P1P2∣<δ 时,都有
∣ f ( P 1 ) − f ( P 2 ) ∣ < ε \left|f\left(P_{1}\right)-f\left(P_{2}\right)\right|<\varepsilon ∣f(P1)−f(P2)∣<ε
成立.
原文链接:高等数学 9.1多元函数的基本概念