深度学习入门：神经网络

文章目录

一、深度学习基础认知
二、神经网络核心构造解析
- [2.1 神经元的基本原理](#2.1 神经元的基本原理)
- [2.2 感知器：最简单的神经网络](#2.2 感知器：最简单的神经网络)
- [2.3 多层感知器：引入隐藏层解决非线性问题](#2.3 多层感知器：引入隐藏层解决非线性问题)
- - [2.3.1 多层感知器的结构特点](#2.3.1 多层感知器的结构特点)
  - [2.3.2 偏置节点的作用](#2.3.2 偏置节点的作用)
  - [2.3.3 多层感知器的计算过程](#2.3.3 多层感知器的计算过程)
三、神经网络训练核心方法
- [3.1 损失函数：衡量预测误差](#3.1 损失函数：衡量预测误差)
- [3.2 正则化惩罚：防止过拟合](#3.2 正则化惩罚：防止过拟合)
- [3.3 梯度下降：优化权重参数](#3.3 梯度下降：优化权重参数)
- - [3.3.1 核心概念](#3.3.1 核心概念)
  - [3.3.2 梯度下降的步骤](#3.3.2 梯度下降的步骤)
- [3.4 BP 神经网络：反向传播优化](#3.4 BP 神经网络：反向传播优化)
- - [3.4.1 BP 神经网络的步骤](#3.4.1 BP 神经网络的步骤)

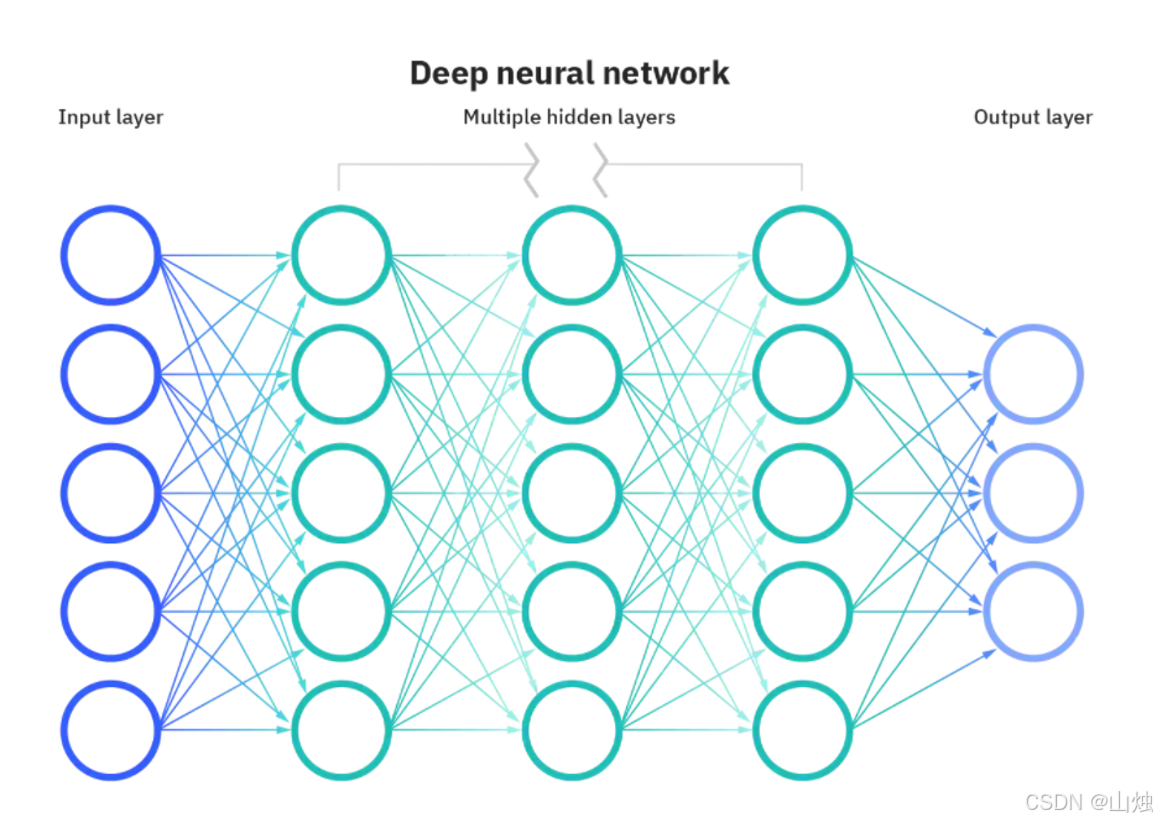
一、深度学习基础认知

首先，我们要明确深度学习在人工智能领域的定位。深度学习（DL, Deep Learning）是机器学习（ML, Machine Learning）领域中一个重要的研究方向，而神经网络又是深度学习的核心载体，三者的关系可以简单理解为：人工智能包含机器学习，机器学习包含深度学习，深度学习以神经网络为核心技术支撑。

简单来说，深度学习就是通过构建多层神经网络，让机器从大量数据中自主学习特征和规律，从而实现对未知数据的预测或分类。比如我们常见的图像识别、自然语言处理等应用，背后都离不开深度学习技术的支持。

二、神经网络核心构造解析

神经网络是深度学习的"灵魂"，它由大量的节点（神经元）和节点间的连接构成。下面我们从基础组件到复杂结构，一步步拆解神经网络的构造。

2.1 神经元的基本原理

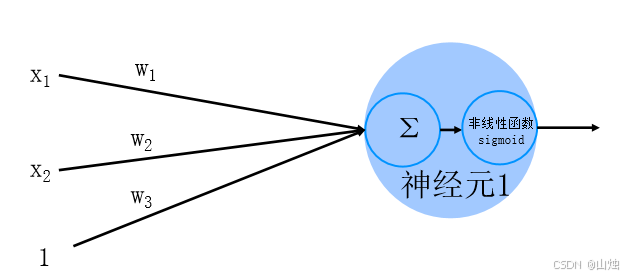
神经元是神经网络的最小单位，其核心是通过线性计算与非线性激活函数的结合，实现对输入信息的处理。

线性计算部分 ：神经元会接收多个输入信号（如 x 1 , x 2 , x 3 x_1, x_2, x_3 x1,x2,x3），每个输入信号都对应一个权重（ w 1 , w 2 , w 3 w_1, w_2, w_3 w1,w2,w3），表示该输入的重要程度。首先会计算输入与权重的加权和，公式如下：
z = w 1 x 1 + w 2 x 2 + w 3 x 3 + b z = w_1x_1 + w_2x_2 + w_3x_3 + b z=w1x1+w2x2+w3x3+b

其中 b b b 是偏置项，用于调整神经元的激活阈值。为了方便计算，我们可以将偏置项转化为权重形式（令 x 3 = 1 , w 3 = b x_3 = 1, w_3 = b x3=1,w3=b），此时公式可简化为 z = w 1 x 1 + w 2 x 2 + w 3 × 1 z = w_1x_1 + w_2x_2 + w_3 \times 1 z=w1x1+w2x2+w3×1，这种形式更便于后续的矩阵运算。
非线性激活函数 ：经过线性计算得到的 z z z 会传入激活函数，引入非线性特性。常用的激活函数是 sigmoid 函数，它能将输出值映射到 0 到 1 之间，公式为：
g ( z ) = 1 1 + e − z g(z) = \frac{1}{1 + e^{-z}} g(z)=1+e−z1

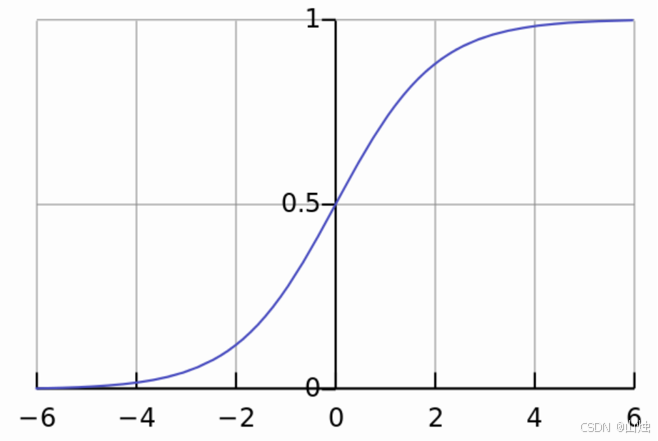
为什么需要非线性激活函数？因为如果只有线性计算，无论神经网络有多少层，最终的输出仍然是输入的线性组合，无法处理复杂的非线性问题（如图像中的边缘、纹理等特征）。

2.2 感知器：最简单的神经网络

感知器是由两层神经元组成的神经网络，是神经网络的"雏形"。它的结构非常简单：

输入层：接收数据特征，节点数与特征维度一致（如输入数据是 3 维特征，输入层就有 3 个节点）。
输出层 ：输出预测结果，节点数与目标维度一致（分类问题，输出层有 1 个节点）。

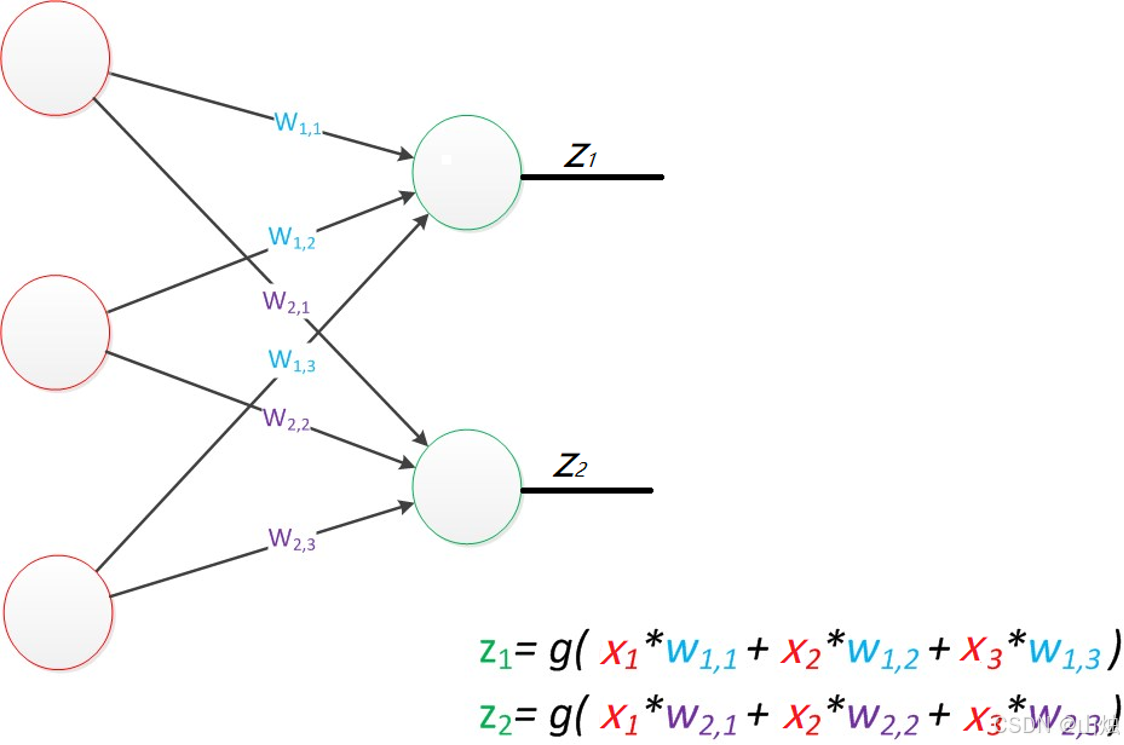
感知器的计算过程可以用矩阵乘法表示。假设输入特征向量为 x = [ x 1 x 2 x 3 ] x = \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} x= x1x2x3 ，权重矩阵为

W = [ w 11 w 12 w 13 w 21 w 22 w 23 ] W = \begin{bmatrix} w_{11} & w_{12} & w_{13} \\ w_{21} & w_{22} & w_{23} \end{bmatrix} W=[w11w21w12w22w13w23]，则输出 z z z 的计算如下：

z = g ( W × x ) z = g(W \times x) z=g(W×x)

其中 g g g 是激活函数。需要注意的是，感知器只能处理线性可分的数据（如用一条直线就能将两类数据分开的情况），无法处理非线性可分问题（如异或问题）。

2.3 多层感知器：引入隐藏层解决非线性问题

为了解决感知器的局限性，我们在输入层和输出层之间增加了隐藏层 ，形成了多层感知器（MLP）。隐藏层是神经网络能处理非线性问题的关键，其核心作用是通过多层非线性变换，逐步提取数据中的复杂特征。

2.3.1 多层感知器的结构特点

输入层 ：节点数固定，与特征维度匹配（如输入是 6 维特征，输入层有 6 个节点 x 1 , x 2 , . . . , x 6 x_1, x_2, ..., x_6 x1,x2,...,x6）。
隐藏层：节点数可自由设定，目前没有统一的理论指导，通常根据经验或实验调整（比如先尝试 32、64、128 个节点，选择模型效果最好的数量）。
输出层：节点数固定，与目标维度匹配（如多分类有 3 个类别，输出层有 3 个节点）。

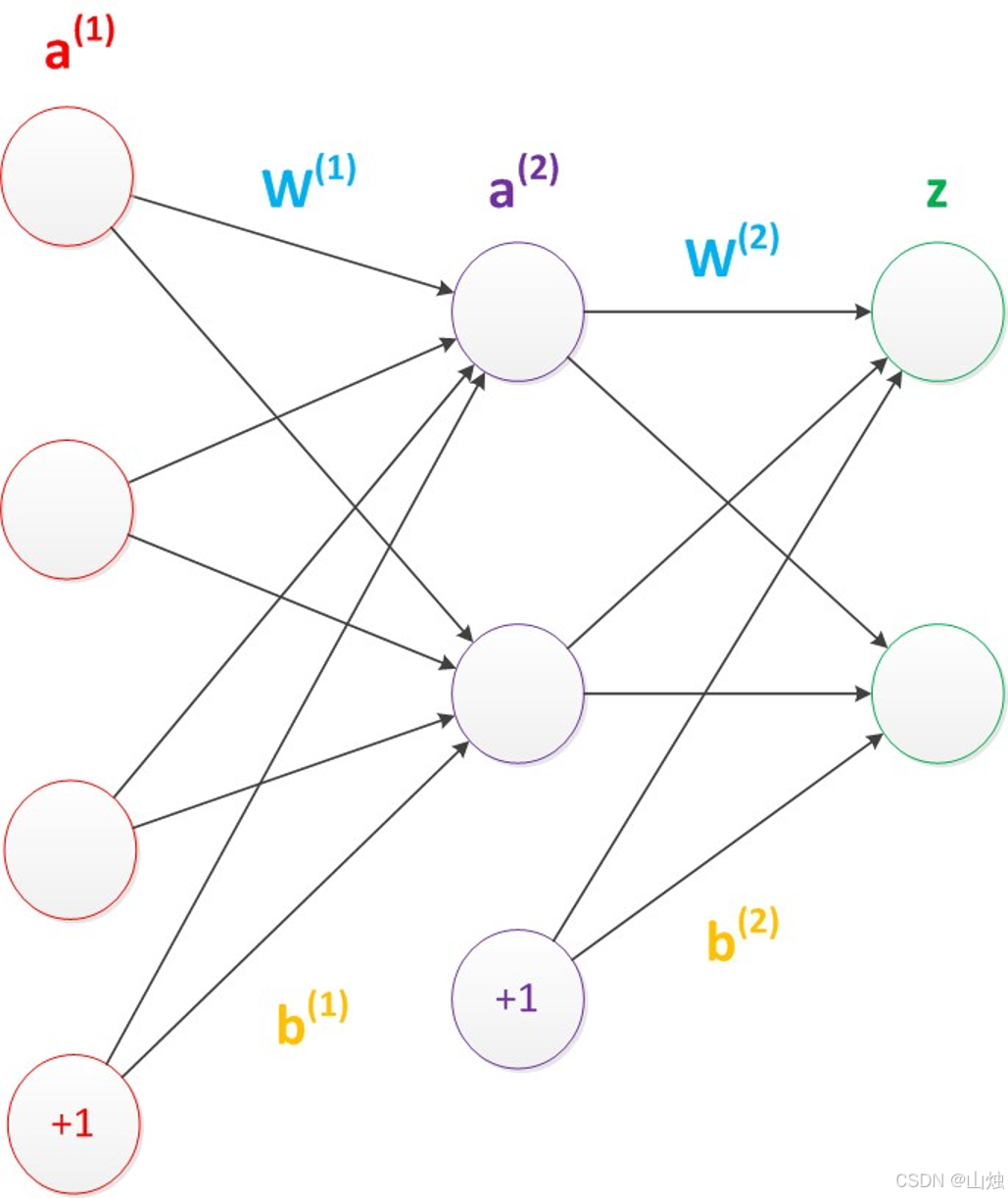
2.3.2 偏置节点的作用

在神经网络的每个层次中（除输出层外），都会默认存在一个偏置节点。它的特点是：

存储值永远为 1，只负责提供偏置项，不接收前一层的输入（没有箭头指向它）。
作用是调整神经元的激活阈值，让模型能更好地拟合数据（比如当所有输入都为 0 时，偏置项可以让神经元仍然有输出）。

2.3.3 多层感知器的计算过程

以"输入层→1 个隐藏层→输出层"的结构为例，计算过程分为两步：

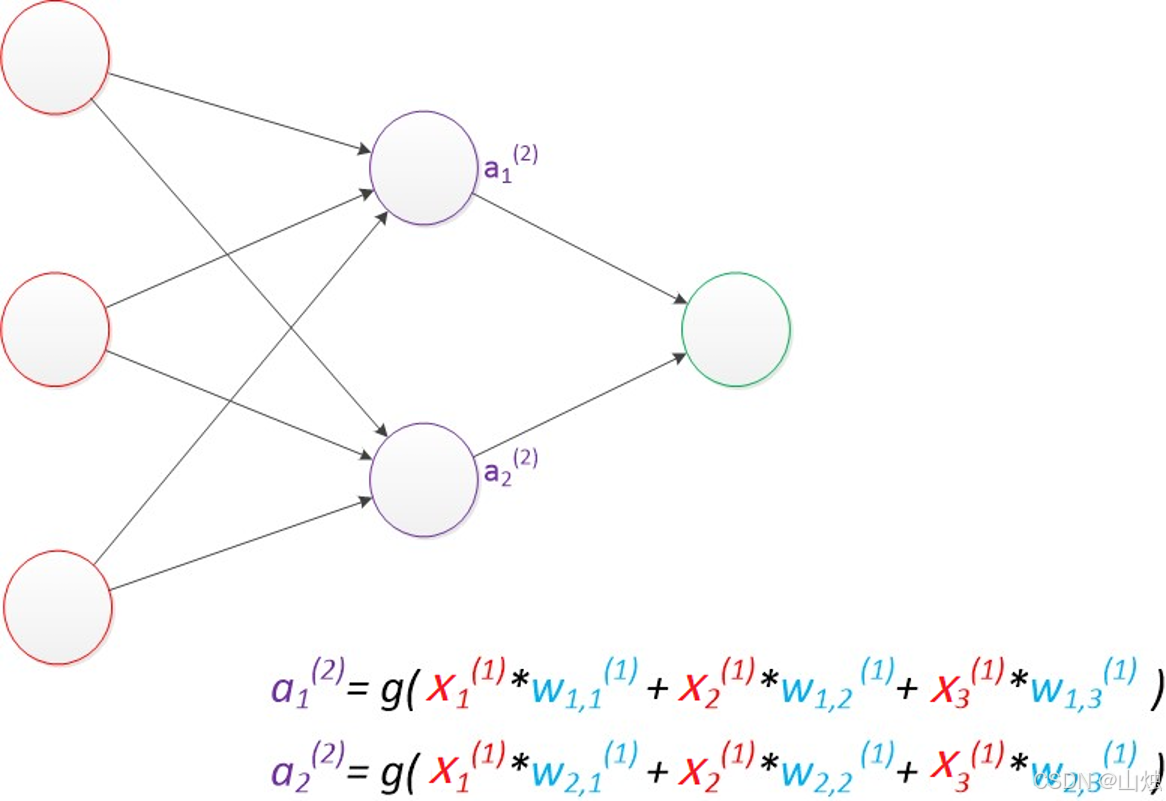
隐藏层计算 ：输入层节点的输出作为隐藏层节点的输入，经过加权和与激活函数后，得到隐藏层的输出 a 1 ( 2 ) a_1^{(2)} a1(2), a 2 ( 2 ) a_2^{(2)} a2(2)（上标 2 表示隐藏层是第 2 层）：
a 1 ( 2 ) = g ( x 1 w 11 ( 2 ) + x 2 w 12 ( 2 ) + x 3 w 13 ( 2 ) ) a_1^{(2)} = g(x_1w_{11}^{(2)} + x_2w_{12}^{(2)} + x_3w_{13}^{(2)}) a1(2)=g(x1w11(2)+x2w12(2)+x3w13(2))
a 2 ( 2 ) = g ( x 1 w 21 ( 2 ) + x 2 w 22 ( 2 ) + x 3 w 23 ( 2 ) ) a_2^{(2)} = g(x_1w_{21}^{(2)} + x_2w_{22}^{(2)} + x_3w_{23}^{(2)}) a2(2)=g(x1w21(2)+x2w22(2)+x3w23(2))
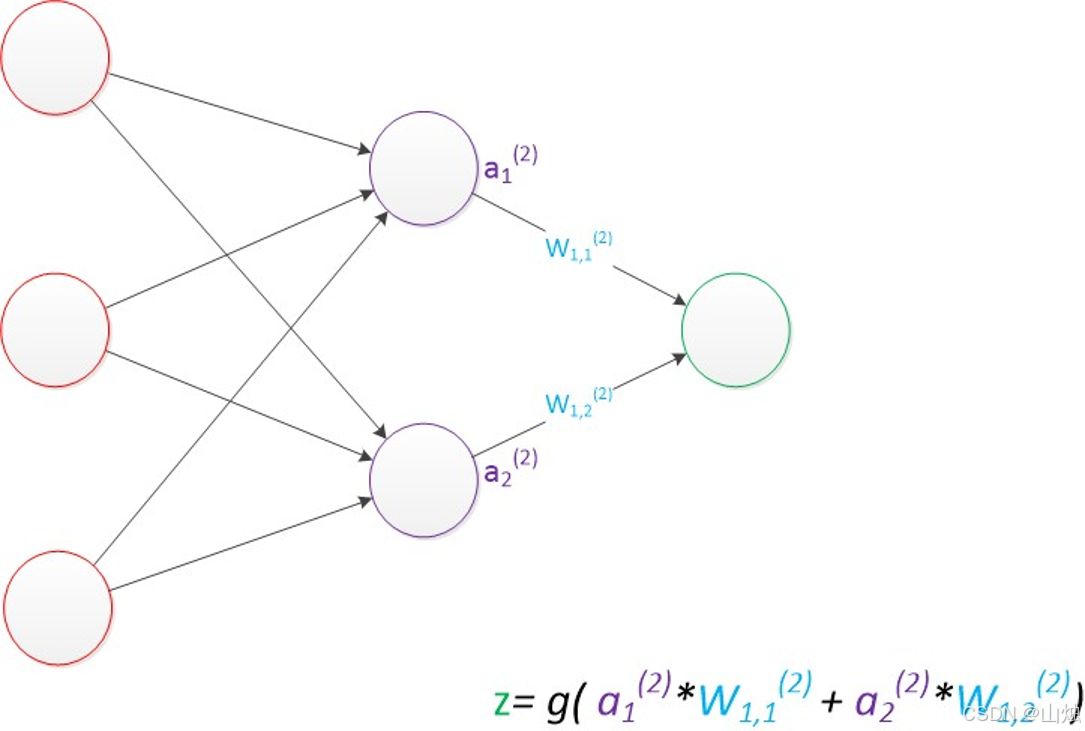
输出层计算 ：隐藏层的输出作为输出层节点的输入，再次经过加权和与激活函数后，得到最终的预测结果 z z z：
z = g ( a 1 ( 2 ) w 11 ( 3 ) + a 2 ( 2 ) w 12 ( 3 ) ) z = g(a_1^{(2)}w_{11}^{(3)} + a_2^{(2)}w_{12}^{(3)}) z=g(a1(2)w11(3)+a2(2)w12(3))

（上标 3 表示输出层是第 3 层）

三、神经网络训练核心方法

神经网络的训练过程，本质上是通过调整权重参数，让模型的预测结果尽可能接近真实值。这个过程主要包括损失函数计算、正则化惩罚、梯度下降优化和反向传播四个关键步骤。

3.1 损失函数：衡量预测误差

损失函数（Loss Function）用于量化模型预测值与真实值之间的误差，误差越小，模型效果越好。常用的损失函数有以下几种：

损失函数类型	适用场景	核心公式（简化版）
0-1 损失函数	分类问题	L = 1 L = 1 L=1 （预测错误）， L = 0 L = 0 L=0 （预测正确）
均方差损失	回归问题	L = 1 n ∑ i = 1 n ( y i − y ^ i ) 2 L = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 L=n1∑i=1n(yi−y^i)2 （ y i y_i yi 真实值， y ^ i \hat{y}_i y^i 预测值）
平均绝对差损失	回归问题	L = 1 n ∑ i = 1 n ∣ y i − y ^ i ∣ L = \frac{1}{n} \sum_{i=1}^{n} \lvert y_i - \hat{y}_i \rvert L=n1∑i=1n∣yi−y^i∣
交叉熵损失	分类问题（尤其是多分类）	L = − ∑ c = 1 M y i c log ⁡ ( p i c ) L = -\sum_{c=1}^{M} y_{ic} \log(p_{ic}) L=−∑c=1Myiclog(pic) （ M M M 类别数， y i c y_{ic} yic 真实标签， p i c p_{ic} pic 预测概率）
合页损失	支持向量机等分类模型	L = max ⁡ ( 0 , 1 − y i y ^ i ) L = \max(0, 1 - y_i \hat{y}_i) L=max(0,1−yiy^i)

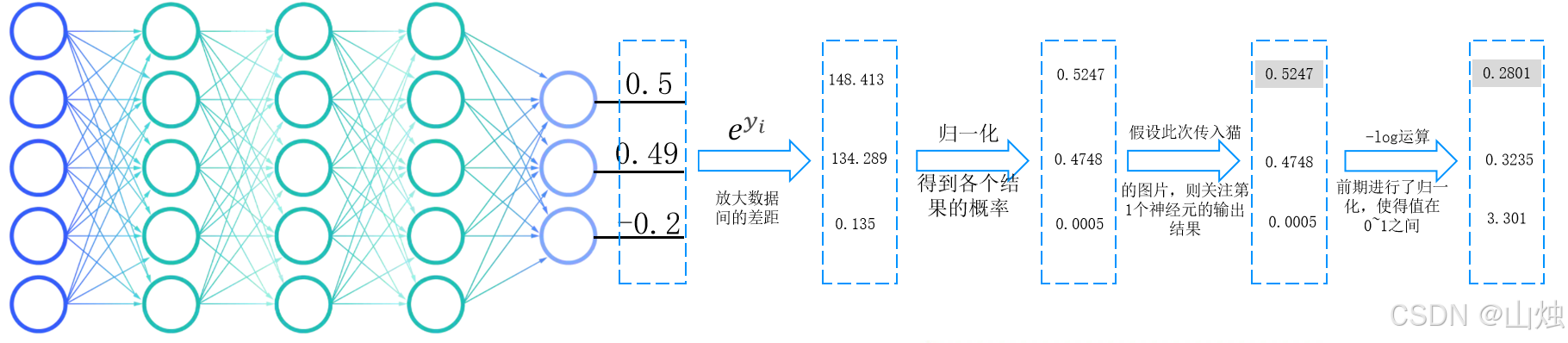
以多分类问题的交叉熵损失为例，假设我们要识别猫、狗、鸟三类图像，输入一张猫的图片：

模型输出层会给出三个预测值（如 148.413、134.289、0.135），首先通过归一化将其转化为 0~1 之间的概率（如 0.4748、0.5247、0.0005）。
真实标签为"猫"，对应的 y i c y_{ic} yic 为 [1, 0, 0]（猫的标签为 1，其他为 0）。
代入交叉熵损失公式，计算得到损失值：
L = − ( 1 × log ⁡ ( 0.5247 ) + 0 × log ⁡ ( 0.4748 ) + 0 × log ⁡ ( 0.0005 ) ) ≈ 0.645. L = -(1 \times \log(0.5247) + 0 \times \log(0.4748) + 0 \times \log(0.0005)) \approx 0.645. L=−(1×log(0.5247)+0×log(0.4748)+0×log(0.0005))≈0.645.
若模型预测错误（如将猫预测为狗，概率为 0.9），则损失值会显著增大，从而提示模型需要调整参数。

3.2 正则化惩罚：防止过拟合

过拟合是神经网络训练中常见的问题，指模型在训练数据上表现很好，但在测试数据上表现很差（模型"死记硬背"了训练数据，没有学到通用规律）。正则化惩罚的核心是通过限制权重参数的大小，让模型更"简单"，从而减少过拟合。

常用的正则化方法有 L1 正则化和 L2 正则化：

L1 正则化 ：对权重参数的绝对值求和，公式为 ∑ i ∣ w i ∣ \sum_i |w_i| ∑i∣wi∣。它会让部分权重变为 0，实现特征选择（即忽略不重要的特征）。
L2 正则化 ：对权重参数的平方求和，公式为 ∑ i w i 2 \sum_i w_i^2 ∑iwi2。它会让权重参数都变得较小，避免某一个特征对模型影响过大。

举个例子：假设输入向量为 x = [ 1 , 1 , 1 , 1 ] x = [1, 1, 1, 1] x=[1,1,1,1]，有两个权重向量 w 1 = [ 1 , 0 , 0 , 0 ] w_1 = [1, 0, 0, 0] w1=[1,0,0,0] 和 w 2 = [ 0.25 , 0.25 , 0.25 , 0.25 ] w_2 = [0.25, 0.25, 0.25, 0.25] w2=[0.25,0.25,0.25,0.25]。两者与输入的乘积都是 1，但：

w 1 w_1 w1 只依赖第一个输入特征，容易"偏爱"这个特征，导致过拟合。
w 2 w_2 w2 均匀利用了所有输入特征，能学到更通用的规律，泛化能力更强。

正则化惩罚会更倾向于选择 w 2 w_2 w2 这样的权重向量。

3.3 梯度下降：优化权重参数

梯度下降是调整权重参数的核心算法，其目标是找到损失函数的最小值（即模型误差最小的状态）。

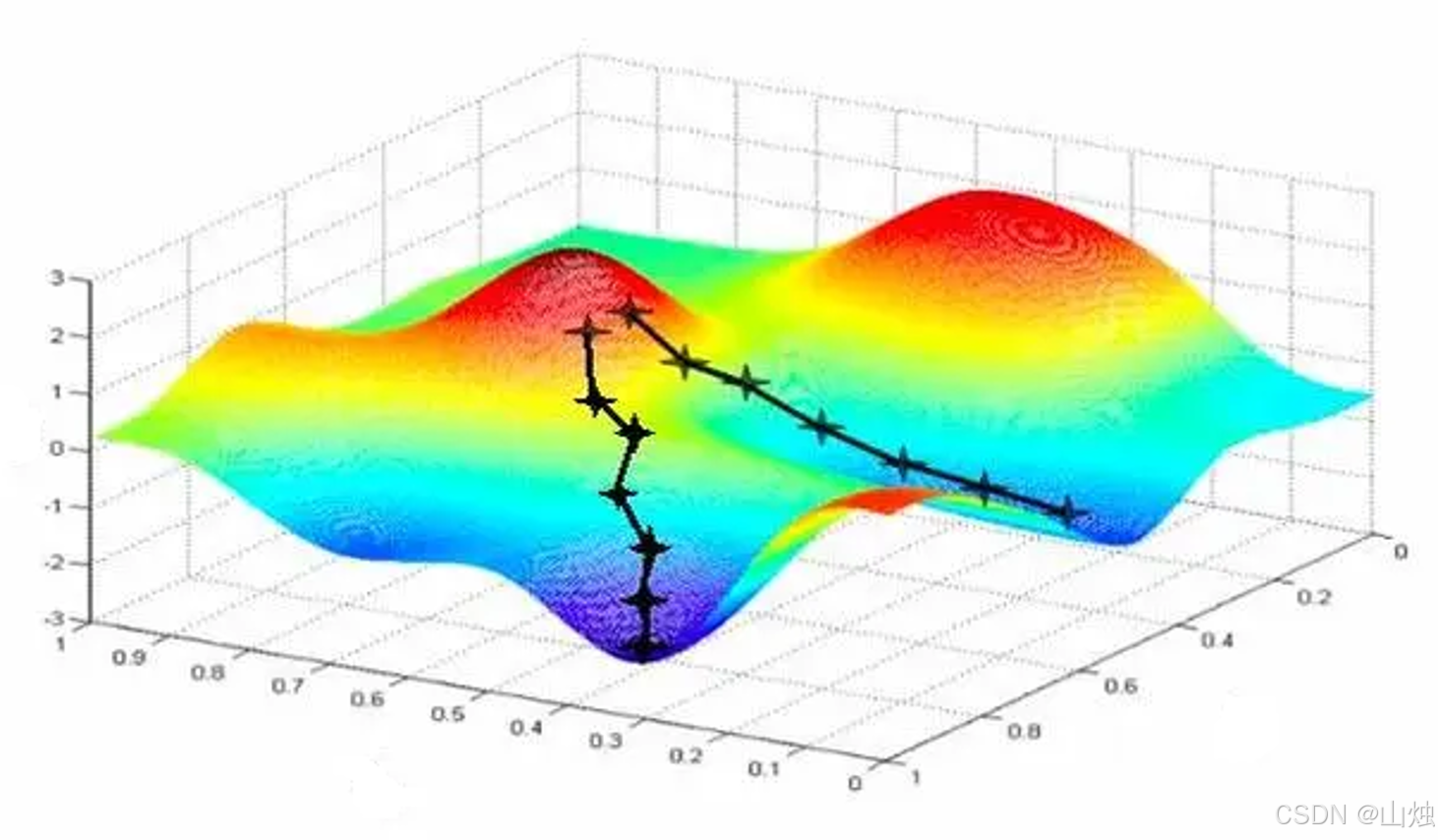
3.3.1 核心概念

偏导数 ：对于多变量函数（如损失函数 L ( w 0 , w 1 , w 2 ) L(w_0, w_1, w_2) L(w0,w1,w2)），偏导数表示函数对某一个变量的变化率（其他变量固定）。比如 ∂ L ∂ w 0 \frac{\partial L}{\partial w_0} ∂w0∂L 表示当 w 1 , w 2 w_1, w_2 w1,w2 固定时， w 0 w_0 w0 变化 1 个单位，损失函数 L L L 的变化量。
梯度：由所有偏导数构成的向量，方向是损失函数值增长最快的方向。因此，我们要沿着梯度的反方向调整权重，才能让损失函数值下降（即找到最小值）。
学习率（步长）：决定每次调整权重的幅度。学习率过大会导致损失函数震荡，无法收敛；学习率过小会导致训练速度极慢，需要大量迭代。通常需要通过实验调整（如 0.001、0.01、0.1）。

3.3.2 梯度下降的步骤

随机初始化所有权重参数（如 w 0 , w 1 , w 2 w_0, w_1, w_2 w0,w1,w2）。
计算当前权重下的损失函数值 L L L。
计算损失函数对每个权重的偏导数（即梯度）。
沿着梯度反方向更新权重： w n e w = w o l d − 学习率 × ∂ L ∂ w o l d w_{new} = w_{old} - 学习率 \times \frac{\partial L}{\partial w_{old}} wnew=wold−学习率×∂wold∂L
重复步骤 2~4，直到损失函数值小于预设阈值（或达到最大迭代次数）。

3.4 BP 神经网络：反向传播优化

BP（Back-propagation，反向传播）是多层神经网络训练的核心算法，它结合了正向传播和反向传播，实现权重的高效更新。

3.4.1 BP 神经网络的步骤

正向传播 ：从输入层到输出层，计算每个层的输出，最终得到模型的预测结果 y ^ \hat{y} y^。
计算损失函数 ：根据预测结果 y ^ \hat{y} y^ 和真实标签 y y y，使用交叉熵损失等函数计算损失值 L L L。
反向传播：从输出层到输入层，计算损失函数对每个权重的偏导数（梯度）。由于多层神经网络的损失函数是复合函数，需要使用链式法则（即先计算输出层的梯度，再逐步推导隐藏层、输入层的梯度）。
权重更新：根据反向传播得到的梯度，使用梯度下降法更新所有权重参数。
循环迭代：重复正向传播→损失计算→反向传播→权重更新的过程，直到模型收敛。