Unity笔记(六)——Mathf、三角函数、坐标系、向量

写在前面：

写本系列**(自用)**的目的是回顾已经学过的知识、记录新学习的知识或是记录心得理解，方便自己以后快速复习，减少遗忘。主要是C#代码部分。

一、Mathf

Mathf是Unity专门封装的，不仅包含Math中的数学相关计算方法，还多了一些适用于游戏开发的方法。

1、Mathf中的常用方法

(1)只计算1次的方法

简单的方法都放在代码注释中说明，这里只提几个需要特别说明的方法：

1、钳制函数/夹紧函数，Clamp。需要传入三个数：需要打印的数、最小数、最大数。如果需要打印的数比最小数还小，就打印最小数；如果需要打印的数比最大数还大，就打印最大数；在范围内则直接输出需要打印的数。例如：Mathf.Clamp(10, 11, 20);打印11，Mathf.Clamp(21, 11, 20);打印20，Mathf.Clamp(15, 11, 20);打印15。

2、一个数的n次幂，Pow。传入两个数，第一个是底数，第二个是次数。如4的2次方Mathf.Pow(4, 2);

3、判断正负数，Sign。如果是正数返回1，负数返回-1Mathf.Sign(-1);返回-1。需要注意的是，该函数认为0为正数。

cs 复制代码

void Start()
{
    //取π - PI
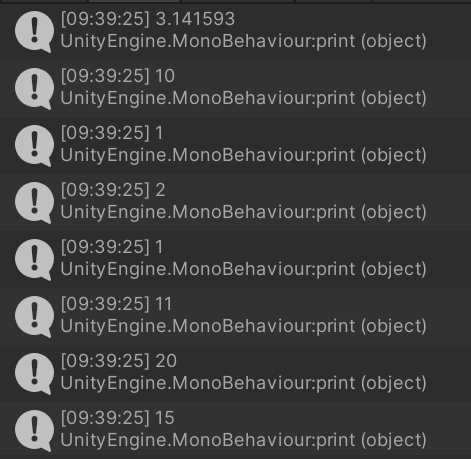
    print(Mathf.PI);

    //取绝对值 -Abs
    print(Mathf.Abs(-10));

    float f = 1.3f;
    int i = (int)f;
    //强转默认的是向下取整
    print(i);
    //向上取整 - CeilToInt
    print(Mathf.CeilToInt(f));

    //向下取整 - FloorToInt
    print(Mathf.FloorToInt(f));

    //钳制函数/夹紧函数 -Clamp
    print(Mathf.Clamp(10, 11, 20));
    print(Mathf.Clamp(21, 11, 20));
    print(Mathf.Clamp(15, 11, 20));

    //获取最大值 - Max
    print(Mathf.Max(1, 2, 3, 4, 5, 6));

    //获取最小值 - Min
    print(Mathf.Min(1, 2, 3));

    //一个数的n次幂 - Pow
    print(Mathf.Pow(4, 2));

    //四舍五入 - RoundToInt
    print(Mathf.RoundToInt(1.3f));

    //返回一个数的平方根 - Sqrt
    print(Mathf.Sqrt(4));

    //判断一个数是否是2的n次方 - IsPowerOfTwo
    //是的话返回true
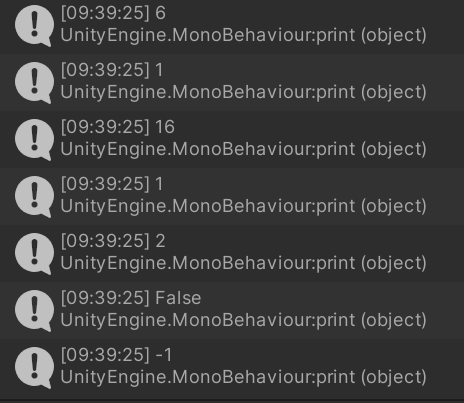
    print(Mathf.IsPowerOfTwo(6));

    //判断正负数 - Sign
    print(Mathf.Sign(-1));

}

(2)会多次计算的方法

插值运算，lerp，语法为：result = Mathf.Lerp(start, end, t);，其中蕴含的计算公式为 result = start + (end - start)*t。主要有两种用法：

1、每帧改变start的值，变化速度先快后慢，位置无限接近end但是不会到end的位置。start初始值 = 0 。start = Mathf.Lerp(start, 10, Time.deltaTime);结合计算公式就不难理解

2、每帧改变t的值，变化速度匀速，位置每帧接近，当t>=1时，得到结果。其中，time、result的初始值都为0。time += Time.deltaTime;result = Mathf.Lerp(start, 10, time);

结合这个公式可以实现一个物体跟随另一个物体移动。

cs 复制代码

float start = 0;
float result = 0;
float time = 0;

void Update()
{
    //每帧改变start的值，变化速度先快后慢，位置无限接近end但是不会到end的位置
    start = Mathf.Lerp(start, 10, Time.deltaTime);

    //每帧改变t的值，变化速度匀速，位置每帧接近，当t>=1时，得到结果
    time += Time.deltaTime;
    result = Mathf.Lerp(start, 10, time);
}

二、三角函数

由π rad = 180°可知：

1 rad = 180°/π≈57.3°、1° = π/180 rad ≈0.01745rad

故，弧度×57.3＝对应角度；角度×0.01745 = 对应弧度

1、弧度与角度的相互转化

弧度转角度需要×57.3，为了方便记忆，可以直接使用弧度×Mathf.Rad2Deg，这里面的值≈57.3。同理，角度转弧度只需要×Mathf.Deg2Rad

cs 复制代码

void Start()
{
    //弧度转角度
    float rad = 1;
    float anger = rad * Mathf.Rad2Deg;
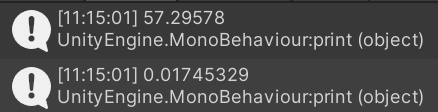
    print(anger);

    anger = 1;
    rad = anger * Mathf.Deg2Rad;
    print(rad);
}

2、三角函数、反三角函数

计算三角函数可以直接调用API，Mathf.Sin()、Mathf.Cos()、需要注意的是，括号内传入的参数需要是弧度制。传入的弧度制可以是角度转为弧度，如下例

反三角函数得到的结果是正弦值或余弦值对应的弧度。可以直接调用API，Mathf.Asin()、Mathf.Acos()，同样需要传入弧度制。

cs 复制代码

void Start()
{
    //三角函数中传入的参数需要是弧度制
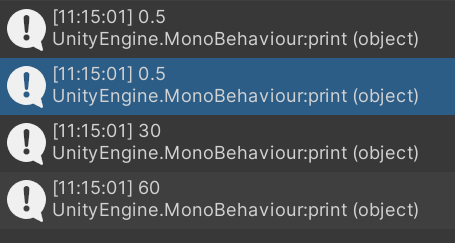
    print(Mathf.Sin(30 * Mathf.Deg2Rad));
    print(Mathf.Cos(60 * Mathf.Deg2Rad));

    //反三角函数得到的结果是正弦值或余弦值对应的弧度
    rad = Mathf.Asin(0.5f);
    print(rad * Mathf.Rad2Deg);
    rad = Mathf.Acos(0.5f);
    print(rad * Mathf.Rad2Deg); 
}

三、坐标系

世界坐标系和物体坐标系都很熟悉了，这里不再赘述。

1、屏幕坐标系：屏幕坐标系是Game窗口显示的屏幕，原点是屏幕左下角。向右为x轴正方向；向上为y轴正方向。最大宽高为Screen.width和Screen.height。

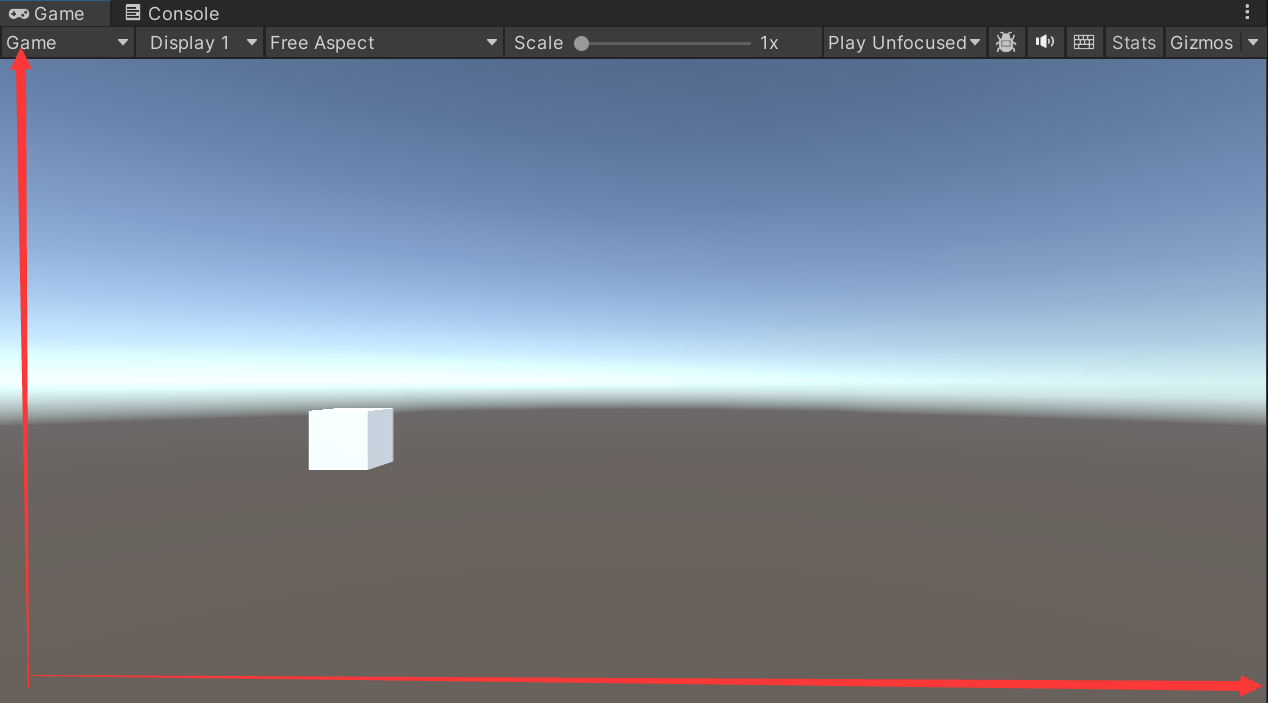
2、视口坐标系。视口坐标系与屏幕坐标系相似，原点再屏幕左下角。向右为x轴正方形，向上为y轴正方形。与屏幕坐标系不同的是，左下角为(0, 0)，右上角为(1, 1)，坐标相当于所占整个屏幕的比例。

1、补充知识

这里补充一些之前没有提到的坐标系知识：

(1)基础

1、屏幕坐标系相关

鼠标在屏幕上的位置可由API：Input.mousePosition得到。屏幕的宽和高分别是Screen.width、Screen.height

2、视口坐标系，指的是摄像机上的视口范围，可在Inspector窗口调整。可用下图的W和H调整。

(2)补充坐标转换

这里补充一些API

世界转屏幕：Camera.main.WorldToScreenPoint

屏幕转世界：Camera.main.ScreenToWorldPoint

世界转视口：Camera.main.WorldToViewportPoint

视口转世界：Camera.main.ViewportToWorldPoint

视口转屏幕：Camera.main.ViewportToScreenPoint 屏幕转视口：Camera.main.ScreenToViewportPoint

四、向量模长和单位向量

1、向量

我们之前常用的Vector3就是三维向量。它有两种几何意义，第一种是位置，代表一个点，例如this.transform.position；第二种是方向，代表一个方向，例如this.transform.forward。

Vector2是二维向量。而一维向量意义不大，一个标量也可以看作一维向量。

2、两点决定一个向量

从A点指向B点的向量为AB向量，计算公式是B-A。Vector3是点还是向量看我们实际应用中为其赋予什么意义。

cs 复制代码

void Start()
{
    Vector3 A = new Vector3(1, 2, 3);
    Vector3 B = new Vector3(5, 1, 5);
    Vector3 AB = B - A;
}

3、零向量和负向量

零向量是全为0的向量，负向量和原向量大小相同方向相反。

cs 复制代码

void Start()
{
    print(Vector3.zero);
    print(-Vector3.forward);
}

4、向量的模长

向量的模长可以直接调用成员属性：.magnitude

cs 复制代码

print(AB.magnitude);

此外，还可以运用之前学习的知识Vector3.Distance(A, B);来获得A、B直接的距离，大小等同于AB模长。

5、单位向量

模长为1的向量，任意一个向量经过归一化就是单位向量。计算方式就是向量的x、y、z分别除向量的模长。可以使用成员属性.normalized来获得单位向量。

cs 复制代码

print(AB.normalized);

五、向量的运算

1、向量的加减乘除

向量的加减乘除直接使用+、-、*、/号即可：

cs 复制代码

void Start()
{
    this.transform.position += new Vector3(1, 2, 3);

    this.transform.position -= new Vector3(1, 2, 3);

    this.transform.localScale *= 2;

    this.transform.localScale /= 2;
}

2、向量点乘

向量a·b的物理意义是，b在a方向上的投影大小，由此在游戏中可以计算出敌人与我方的距离。

(1)调试画线

先补充一个Debug知识：Debug.DrawLine()可以在指定位置画线，传入的前两个参数分别是线段的两个端点，第三个参数可以传入线段的颜色。

cs 复制代码

void Update()
{
    Debug.DrawLine(this.transform.position, this.transform.position + this.transform.forward,Color.red);
}

Debug.DrawRay(); 画的是射线，第一个参数是射线的起点，第二个参数是射线的方向，第三个参数是射线的颜色。这里画的射线也不是无限延伸的。

cs 复制代码

Debug.DrawRay(this.transform.position,this.transform.forward, Color.white);

(2)相关公式

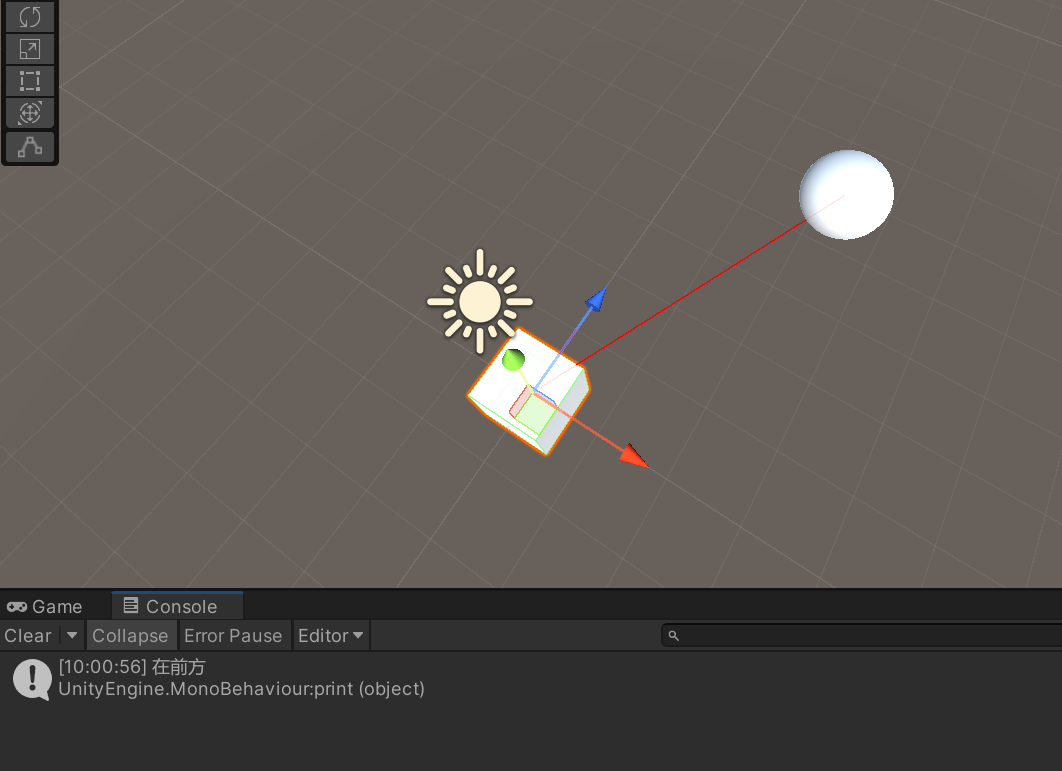
假设有物体A和物体B，想要知道B是在A的前方还是后方，可以通过点乘的知识。用A和B的连线BA向量点乘向量A，就可以知道BA在A方向上的投影大小。如果投影为正，则B在A的前方，若投影为负，则在A的后方。

cs 复制代码

public Transform target;

void Update()
{
    Debug.DrawRay(this.transform.position,this.transform.forward, Color.red);

    Debug.DrawRay(this.transform.position, target.position - this.transform.position, Color.red);

    float dotResult = Vector3.Dot(this.transform.forward, target.position - this.transform.position);

    if(dotResult > 0 )
    {
        print("在前方");
    }
    else
    {
        print("在后方");
    }
}

两个向量之间的夹角可以通过以下公式算出：

(单位向量A，单位向量B）

此外，Unity也提供了API来计算两个向量之间的夹角：Vector3.Angle()，括号里传入两个向量即可

cs 复制代码

print(Vector3.Angle(this.transform.position, target.position-this.transform.position));

3、向量叉乘

两个向量A和B进行叉乘，叉乘的结果垂直于向量A和B所组成的平面。

此外，向量A叉乘向量B，叉乘结果，y大于0证明B在A右侧，y小于0证明B在A左侧。

叉乘可以使用Unity提供的API：Vector3.Cross()，里面传入两个叉乘的向量即可。

cs 复制代码

void Start()
{
    print(Vector3.Cross(A.forward, B.position - A.position));
}

4、向量插值运算

(1)线性插值

向量的线性插值运算与之前提到的插值运算几乎完全相同，不同的就是这里插值的是三维的坐标点。使用的API是Vector3.Lerp()。可以看出，以下代码中的核心A.position = Vector3.Lerp(A.position, target.position, Time.deltaTime);与B.position = Vector3.Lerp(startPos,target.position, time);与插值运算中的两种用法完全相同。

cs 复制代码

public Transform target;
public Transform A;
public Transform B;


private Vector3 startPos;
private float time = 0;
private Vector3 nowTarget;

void Start()
{
    startPos = B.position;
}


// Update is called once per frame
void Update()
{
    //先快后慢
    A.position = Vector3.Lerp(A.position, target.position, Time.deltaTime);

    if(nowTarget != target.position)
    {
        nowTarget = target.position;
        time = 0;
        startPos = B.position;
    }
    //这种匀速运动 当time>=1时，再改变目标位置，它会直接瞬移到目标位置
    time += Time.deltaTime;
    B.position = Vector3.Lerp(startPos,target.position, time);

}

(2)球形插值

球形插值的用法与线性插值完全一样，API改为Vector3.Slerp()，此外，线性插值插值出的线是直线，而球形插值是弧线。

cs 复制代码

public Transform C;

void Update()
{
    C.position = Vector3.Slerp(Vector3.right*10, Vector3.forward*10, time);
}