一、直方图规则化
伽马校正的数学表达为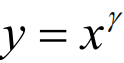 
；图像"aerial.tif"是一幅光散射的航空图像， 析伽马校正中系数
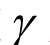系数的影响，对该图像作直方图规则化处理。
1、理论基础
2、代码
Matlab
伽马校正曲线的代码（画出gamma=2^i, i=-3:1:3的曲线）
x = [0:0.01:1];% 初始化灰度值
figure;% 创建图形窗口
% 生成并绘制伽马校正曲线
for i = -3:1:3
y = x.^(2^i);
plot(x, y, 'DisplayName', ['\gamma = 2^{' num2str(i) '}']);
hold on;
end
itle('Gamma Correction Curves');xlabel('Input Intensity');ylabel('Output Intensity');% 添加标题和标签
legend('show');
grid on;% 显示网格和保持纵横比
axis square;
aerial.tif的伽马校正：
O_image = imread('D:\MATLAB\work\DIP\aerial.tif');
% 设置伽马值
gamma = 1/4;gamma1 = 1/2;gamma2 = 2;gamma3 = 3;gamma4 = 4;
% 对图像进行伽马校正
C_image = imadjust(O_image,[],[],gamma); [C_image x] = imhist(C_image);j = histeq(O_image ,C_image );
C1_image = imadjust(O_image,[],[],gamma1); [C1_image x1] = imhist(C1_image);j1 = histeq(O_image ,C1_image );
C2_image = imadjust(O_image,[],[],gamma2); [C2_image x2] = imhist(C2_image);j2 = histeq(O_image ,C2_image );
C3_image = imadjust(O_image,[],[],gamma3); [C3_image x3] = imhist(C3_image);j3 = histeq(O_image ,C3_image );
C4_image = imadjust(O_image,[],[],gamma4); [C4_image x4] = imhist(C4_image);j4 = histeq(O_image ,C4_image );
% 显示原始图像和伽马校正直方图规则化后的图像
subplot(2,3,1);
imshow(j);title('Gamma=1/4 Corrected Image');
subplot(2,3,2);
imshow(j1);title('Gamma=1/2 Corrected Image');
subplot(2,3,3);
imshow(O_image);title('Original Image');
subplot(2,3,4);
imshow(j2);title('Gamma=2 Corrected Image');
subplot(2,3,5);
imshow(j3);title('Gamma=3 Corrected Image');
subplot(2,3,6);
imshow(j4);title('Gamma=4 Corrected Image');3、图像分析
伽马校正曲线：
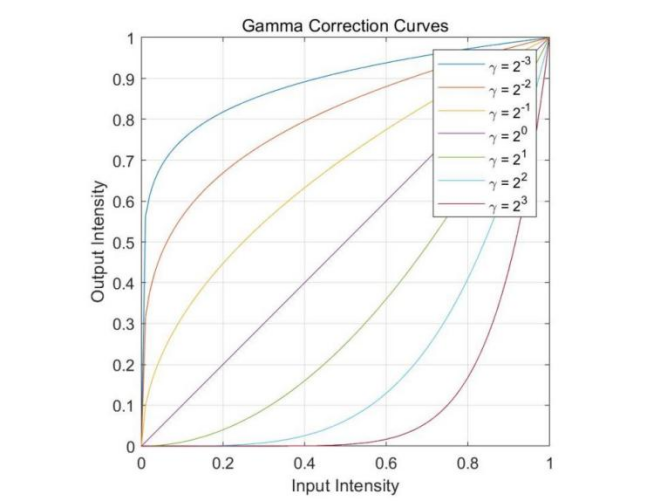aerial.tif的伽马校正：
通过设定不同的gamma（1/4、1/2、2、3、4）值与原图相比得到不同的gamma校正图像。当gamma的值＜1时：gamma=1/4与gamma=1/2相比前者整体变亮程度明显大于后者。特别地，属于原图阴暗部分在gamma=1/4比gamma=1/2更亮，阴影边界得到弱化。当gamma的值＞1时；随着gamma值的变大，明显看出整体光亮程度减小，阴影程度得到不断加深。
4、讨论
讨论gamma系数的取值对图像增强的影响：
（1）gamma取值什么情况下最优？
在伽马校正中，伽马值的选择对图像增强效果有重要影响。从上图gamma取不同值时，图像的明亮程度有明显差异。当gamma值接近1时，图像基本保持原始状态，不会有太大变化。当gamma值小于1时：图像的暗部细节会得到增强，整体图像会变亮。当gamma值大于1时：图像的亮部细节会得到增强，整体图像会变暗。所以在一般情况下，gamma值在0.5到2.0之间的范围内选择，具体取值根据对所需要的图像的特性和需求来确定。
（2）自适应最优值：
自适应方法是指通过算法自动调整模型参数或者超参数的方法，以获得更好的性能。自适应获取最优值的方法可以根据图像的特性和需求来设计，例如基于图像的直方图分布、对比度等特征来动态调整gamma值。
一种常见的自适应方法是通过迭代算法或优化算法来不断调整gamma值，直到达到最佳的增强效果。总的来说，最优gamma值的选择需要根据具体的图像特性和需求来确定，而自适应获取最优值的方法可以在一定程度上提高图像增强的效果。常用的方法是网格搜索和随机搜索。网格搜索是指在一定范围内进行均匀划分，然后枚举每一组超参数组合的方式寻找最优超参数。而随机搜索则是在一定范围内随机采样，然后寻找效果最好的超参数组合。这两种方法都有优缺点，具体选择取决于数据集的大小和计算资源的限制。另外，还有一种更加高效的方法是贝叶斯优化。它可以根据已经尝试过的超参数组合来更新先验概率分布，从而更快地找到最优解。
（3）能否self-adaptive获取最优值？
Self-adaptive方法是一种智能优化算法，通过不断地调整算法参数来提高算法性能。在使用Self-adaptive方法时，gamma是控制搜索方向和步长的参数，它的值越大，搜索方向越集中，步长越小；反之，gamma越小，搜索方向越分散，步长越大。因此，确定gamma最优值对于算法的性能和搜索效果非常重要。在确定gamma的最优值一般通过实验和经验但是可能不够准确和高效。
二、平滑空间滤波器
线性滤波器
（1）图像"lena_gray.bmp"加入了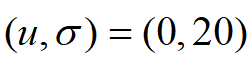
的高斯白噪声，采用均值模板与"理论基础"中的高斯模板对图像进行去噪。
（2）已知二维高斯函数为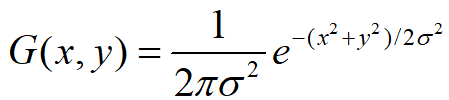
，设计一个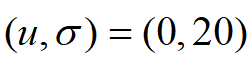的高斯模板，对该图像进行去噪。
1、理论基础
平滑空间滤波器是低频增强的空间滤波技术。它的目的有两类：一是模糊处理，二是降低噪声。
一幅M*N的图像进行一个m*n的加权均值滤波器，滤波的过程如下：
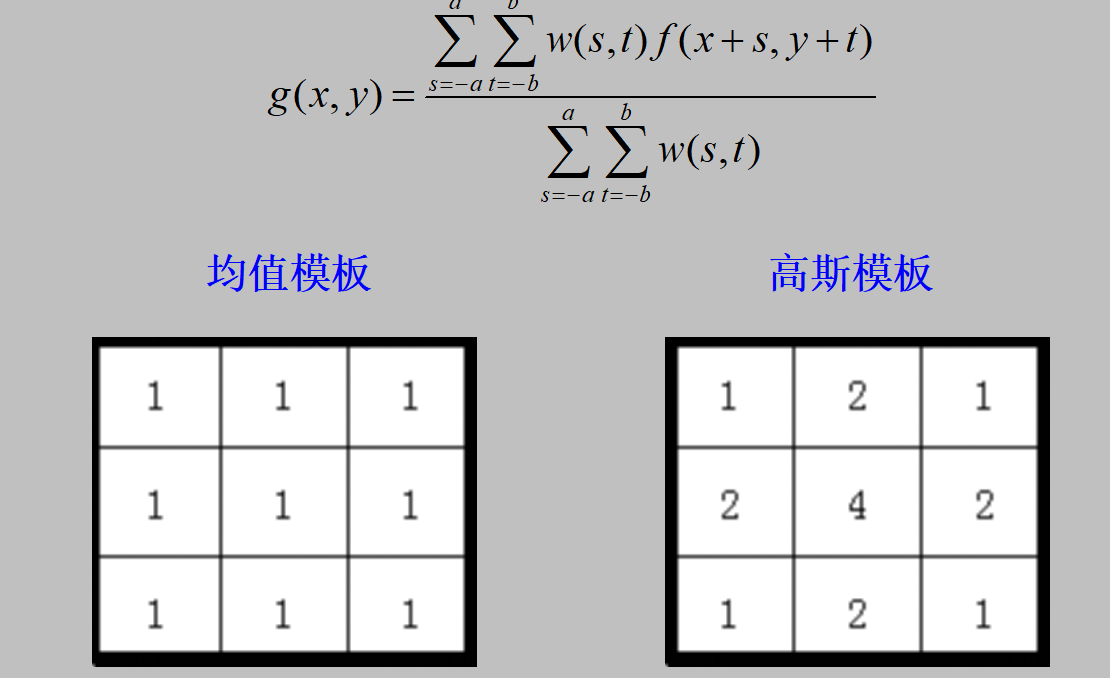
2、代码
Matlab
（1)代码：
img = imread('D:\MATLAB\work\DIP\lena_gray.bmp');
subplot(1,3,1);imshow(img);title('原始图像');
% 定义3x3的均值模板
mean_model = ones(3)/ 9;
mean_filtered_img = imfilter(img, mean_model);% 使用均值滤波进行去噪
subplot(1,3,2);imshow(mean_filtered_img);
title('均值模板去噪后的图像');
% 定义3x3的高斯模板
gaussian_model = [1, 2, 1; 2, 4, 2; 1, 2, 1] / 16;
% 使用高斯滤波进行去噪
gaussian_filtered_img = imfilter(img, gaussian_model);
subplot(1,3,3);imshow(gaussian_filtered_img);title('高斯模板去噪后的图像');
(2)代码：
img = imread('D:\MATLAB\work\DIP\lena_gray.bmp');
subplot(1,3,1);imshow(img);title('原始图像');
[X, Y] = meshgrid(-1:1, -1:1);
sigma = sqrt(20);
gaussian_filter = exp(-(X.^2 + Y.^2) / (2*sigma^2));
gaussian_filter=gaussian_filter/(2*pi*sigma^2);
gaussian_filter = gaussian_filter / sum(gaussian_filter, 'all');
% 使用高斯滤波进行去噪
gaussian_filtered_img = imfilter(img, gaussian_filter);
figure;imshow(gaussian_filtered_img);
title('方差=20的高斯模板去噪后的图像');3、图像分析
使用不同的方法对含有高斯白噪声的灰度图像进行去噪声处理;
采用高斯滤波器主要是对图像对应的数字信号主要是用加权平均函数将结果进行加权之后,用平均值覆盖特殊值进行处理。
均值滤波也称为线性滤波,采用的主要方法为邻域平均法。基本原理是用均值替代原图像中的各个像素值。
从图上明显可以看出，采用均值模板去噪声后得到的图像整体平滑，边缘锐利程度并不如用高斯模板去噪声后得到的图像。
非线性滤波器
图像"lena_gray.bmp"加入了椒盐噪声，采用中值滤波对图像进行处理。
1、理论基础
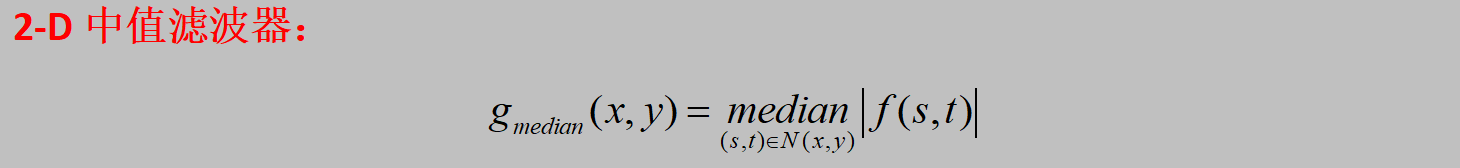
2、代码
Matlab
mg = imread('D:\MATLAB\work\DIP\lena_gray.bmp');
subplot(1,4,1);imshow(img);title('原始图像');
% 添加5%椒盐噪声
noisy_img = imnoise(img, 'salt & pepper', 0.05);
subplot(1,4,2);
imshow(noisy_img);
title('加入椒盐噪声的图像');
% 定义3x3的均值模板
median_filtered_img = medfilt2(noisy_img, [3, 3]);
subplot(1,4,3);
imshow(median_filtered_img);
title('中值滤波去噪后的图像');3、图像分析
加入5%的椒盐噪声以后，再对其用中值滤波进行处理：选取数字图像或数字序列中像素点及其周围临近像素点（一共有奇数个像素点）的像素值，将这些像素值排序，然后将位于中间位置的像素值作为当前像素点的像素值，让周围的像素值接近真实值，从而消除孤立的噪声点。利用中值滤波从而能有效针对椒盐噪声进行去噪处理能得到较好的效果。
三、锐化空间滤波器
一阶求导：边缘检测
采用Sobel算子，对图像"house.jpg"进行水平边缘检测、垂直边缘检测、"水平+垂直"的2-范式的边缘检测。
1、理论基础
2、代码
Matlab
% 读取图像
img = imread('D:\MATLAB\work\DIP\house.jpg');
figure;imshow(img);title('原始图像');
% Sobel算子
sobelx = edge(img, 'Sobel', 'horizontal');
sobely = edge(img, 'Sobel', 'vertical');
% 水平边缘检测
h_edges = uint8(sobelx * 255);
% 垂直边缘检测
v_edges = uint8(sobely * 255);
% "水平+垂直"的2-范式的边缘检测
edges = sqrt(double(h_edges).^2 + double(v_edges).^2);
edges = uint8(edges);
% 显示结果
figure;
subplot(1,3,1);imshow(h_edges);title('Horizontal Edges');
subplot(1,3,2);imshow(v_edges);title('Vertical Edges');
subplot(1,3,3);imshow(edges);title('Combined Edges');3、图像分析
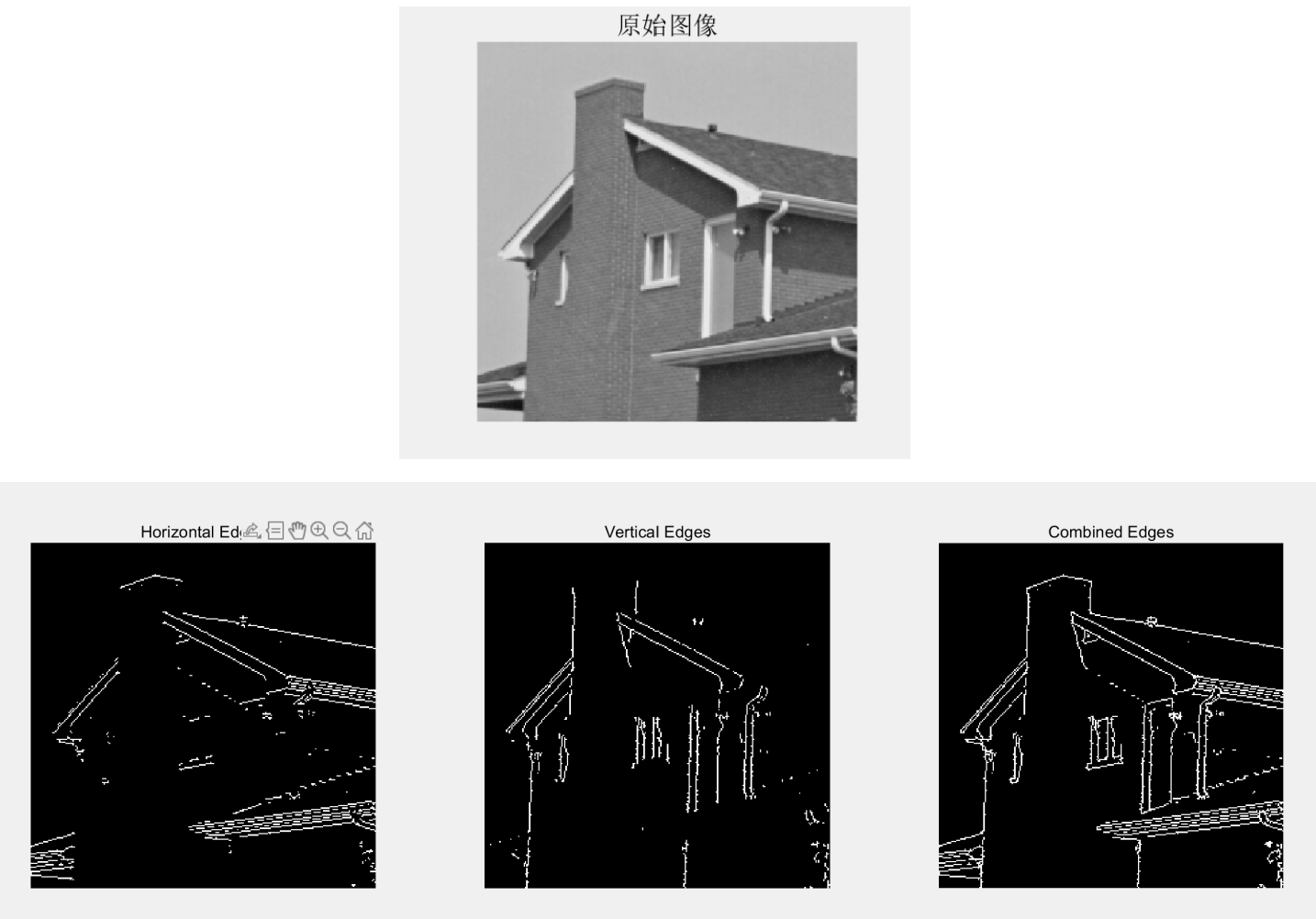
使用sobel算子对其进行水平边缘检测、垂直边缘检测、水平＋垂直的2-范式的边缘检测，明显可以看出第一个图为水平边缘检测注重检测图像水平边缘、第二个为垂直边缘检测，着重检测到原图像在垂直边缘的检测，从第三个图看出既有水平也有垂直的边缘检测是2-范式的边缘检测，所以使用sobel算子得到到对应的边缘检测不错的效果，但是检测的准确程度不是很好，从原图上可以看出检测的细纹理处理的不是很好。
二阶求导：边缘检测
采用Laplacian算子对图像"house.jpg"进行边缘检测。
1、理论基础
2、代码
Matlab
img = imread('D:\MATLAB\work\DIP\house.jpg');
figure;imshow(img);title('原始图像');
h=fspecial('laplacian');%创建一个Laplacian算子
J=imfilter(img ,h,'replicate');%图像滤波，'replicate'边界选项
K=im2bw(J,38/255);%变为二维图像
laplacian_edges = edge(img, 'log');
% 显示结果
figure;
subplot(131),imshow(J);title('单用Laplacian Edges');
subplot(132),imshow(K);title('Laplacian Edges二值图');
subplot(133),imshow(laplacian_edges);title('高斯平滑噪声后Laplacian Edges');3、图像分析
（图1和图2）在使用单使用Laplacian算子通过阈值处理来提取边缘信息，设定一个合理的阈值，将高于或低于该阈值的像素点标记为边缘或非边缘，当阈值取值不够合理时，会发现图片边缘检测到的图片非边缘检测到很多。但是通过图3，在使用拉普拉斯算子之前，通过对图像进行高斯平滑处理，以降低噪声的影响，在进行Laplacian算子边沿检测，效果会更好，比之前使用的sobel算子边缘检测到的会更连续、平滑。
4、讨论
讨论一阶求导与二阶求导在图像处理中的作用？
（1）一阶求导？
一阶导数可以反应出图像灰度梯度的变化情况，例如：sobel算子。
一阶求导可以帮助检测图像中的边缘，因为边缘通常表现为像素值的剧烈变化。通过计算图像的一阶导数，可以找到这些像素值变化最明显的地方，从而检测出图像中的边缘。
一阶求导也可以用于特征提取，例如在图像中检测角点或者其他局部特征。一阶导数可以帮助定位图像中的局部极值点，从而提取出这些特征点。
（2）二阶求导？
二阶导数可以提取出图像的细节同时双响应图像梯度变化情况。例如：Laplacian算子
二阶求导通常用于更精确地检测图像中的边缘。通过计算图像的二阶导数（梯度的梯度），可以获得更加精细的边缘信息，有助于准确地定位边缘的位置和强度。
二阶求导还可以用于纹理分析和特征提取。由于二阶导数可以反映图像中的纹理变化和细节信息，因此在一些纹理分析任务中，二阶求导也被广泛应用。
四、频率域滤波
高通滤波器（锐化）
（1）对于图像"texta.tif"，画出下述三种滤波器及对应的滤波结果图。
（2）通过滤波结果比对，讨论D0, n两个参数对滤波器的影响。
1、理论分析
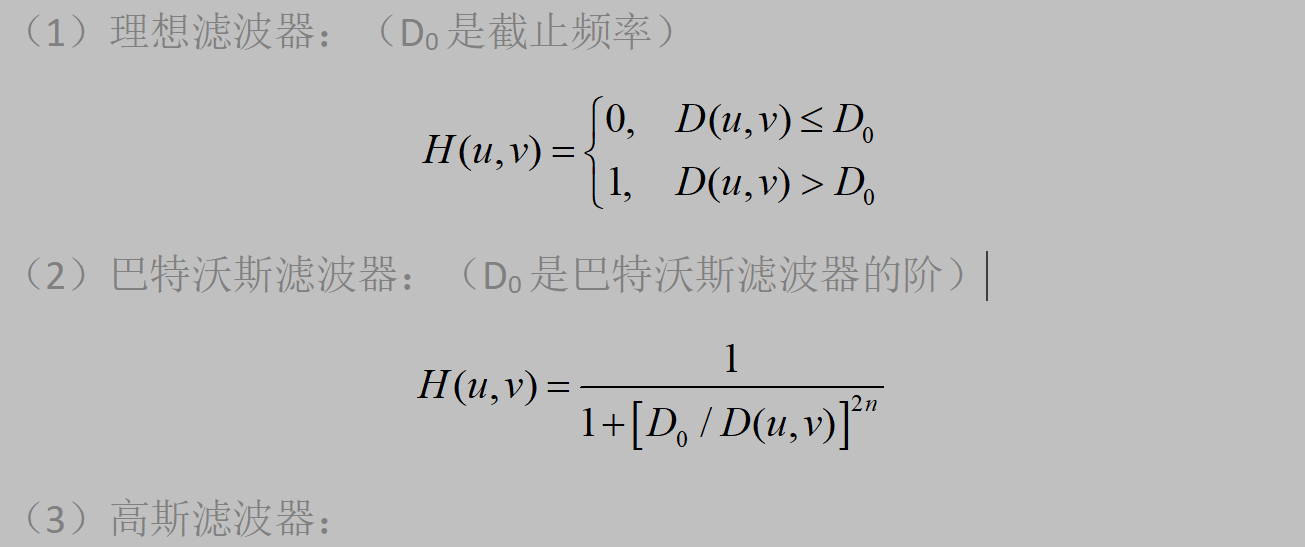
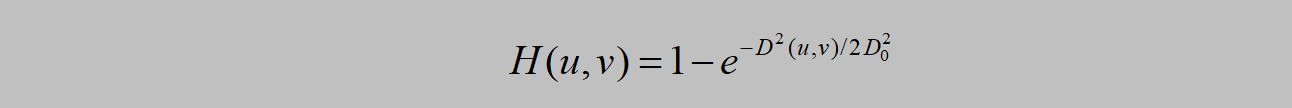
2、代码
Matlab
clc; clear; close all;
img = imread('D:\MATLAB\work\DIP\texta.tif');
subplot(141),imshow(img);title('原始图像');
% 理想高通滤波器
J=fftshift(fft2(im2double(img)));
[a,b]=size(J);a0=round(a/2);b0=round(b/2);
d0=50; % 截止频率
for i=1:a %双重for循环计算频率点(i,j)与频域中心的距离
for j=1:b
distance=sqrt((i-a0)^2+(j-b0)^2);
if distance<=d0 % 当D(i,j)<=D0,置为0
h=0;
else
h=1; % 当D(i,j)>D0,置为1
end
J(i,j)=h*J(i,j);% 频域图像乘以滤波器的系数
end
end
% real函数取元素的实部
J=real(ifft2(ifftshift(J)));% 最后进行二维傅里叶反变换转换为时域图像
subplot(142),imshow(J,[]);title('理想高通滤波所得图像');
% 将巴特沃斯高通滤波器
K=fftshift(fft2(im2double(img)));
[N1,N2]=size(K);%求二维傅里叶变换后图像大小
n=2;n1=round(N1/2);n2=round(N2/2);
d0=30; % 阶数n截止频率
for i=1:N1 %双重for循环计算频率点(i,j)与频域中心的距离
for j=1:N2
distance=sqrt((i-n1)^2+(j-n2)^2);
if distance==0
h=0;
else
h=1/(1+(d0/distance)^(2*n));% 根据巴特沃斯高通滤波器公式为1/(1+[D0/D(i,j)]^2n)
end
K(i,j)=h*K(i,j);% 频域图像乘以滤波器的系数
end
end
% real函数取元素的实部
K=real(ifft2(ifftshift(K)));% 时域图像
subplot(143),imshow(K,[]);title('Butterworth高通滤波图像');
% 高斯高通滤波器
L=fftshift(fft2(im2double(img)));
[a,b]=size(L);a0=round(a/2);b0=round(b/2);
d0=10; % 截止频率D0设置为10
for i=1:a
for j=1:b
distance=sqrt((i-a0)^2+(j-b0)^2); % 公式H(u,v)=e^-[D^2(u,v)/2*D0^2]
h=1-(exp(-(distance^2)/(2*(d0^2)))); % exp表示以e为底的指数函数
L(i,j)=h*L(i,j);% 频域图像乘以滤波器的系数
end
end
L=real(ifft2(ifftshift(L)));% 转换为时域图像
subplot(144),imshow(L,[]); title('高斯高通滤波图像');3、图像分析
通过对理想高通滤波器所得图像分析：高通滤波可保留图像中的高频分量而除去低频分量。图像中的轮廓和内容都对应图像傅里叶频谱中的低频部分，所以高通滤波可以去除图像的轮廓而保留图像的边缘等突变信息。可以观察到较为明显的振铃效应。
通过对高斯高通滤波器所得图像分析：可以明显看出突出了图像中的高频成分来增强细节，以及没有产生振铃效应。
在巴特沃斯高通滤波器处理后，当截止频率较低（d0=10、30、40对比）时，低频内容会被更多保留，图像变得更加清晰，也更加贴合原图像。当截止频率较高时，滤波器会通过更少的高频信息，低频细节大量丢失，图像只保留下大致的轮廓部分。
阶数低（n=1、4、10时）的巴特沃斯滤波器滤波后的图像边缘更加清晰，随着阶数增大，幅频曲线变化剧烈。当阶数n=10时，已经能观察出明显的振铃效应。
低通滤波器（平滑）
（1）对于图像"texta.tif"，画出下述三种滤波器及对应的滤波结果图
（2）当D0=5, 15, 35, 50时，对比滤波结果。
1、理论基础
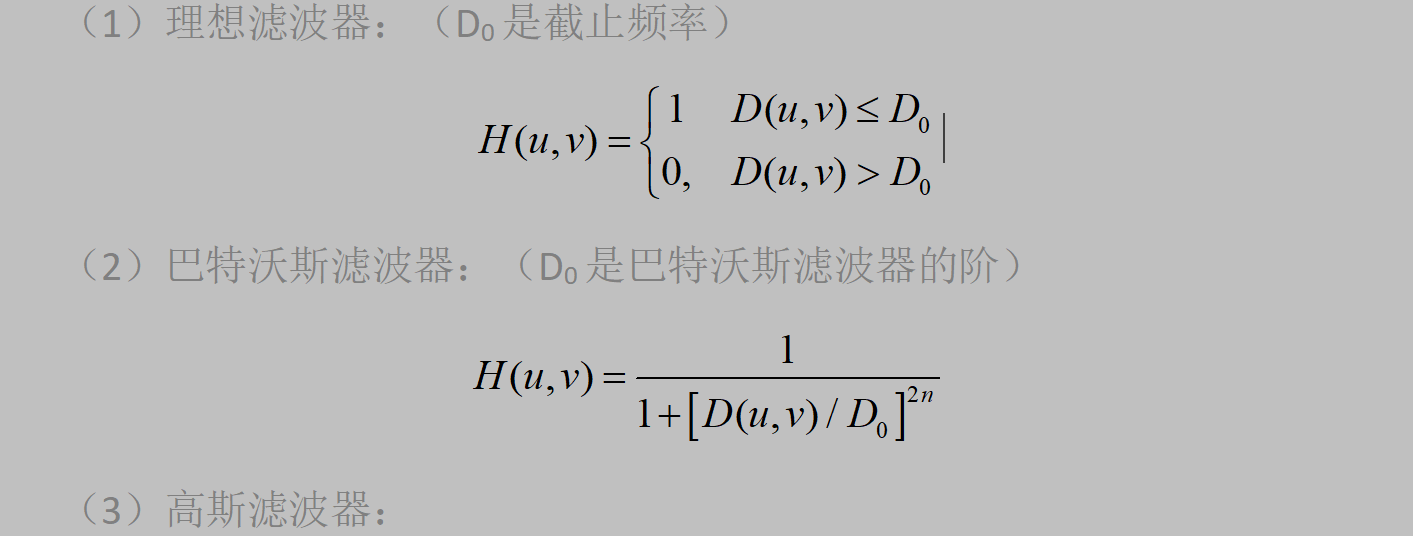
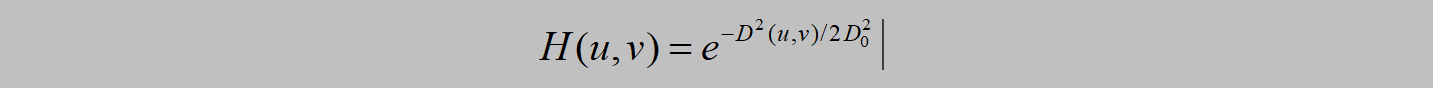
2、代码
Matlab
%读取图像
img = imread('D:\MATLAB\work\DIP\texta.tif');
subplot(141),imshow(img);title('原始图像');
% 理想低通通滤波器
J=fftshift(fft2(im2double(img)));
[a,b]=size(J);a0=round(a/2);b0=round(b/2);
d0=50; % 截止频率D0设置为50
for i=1:a %双重for循环计算频率点(i,j)与频域中心的距离
for j=1:b
distance=sqrt((i-a0)^2+(j-b0)^2);
if distance<=d0 % 当D(i,j)<=D0,置为1
h=1;
else
h=0; % 当D(i,j)>D0,置为0
end
J(i,j)=h*J(i,j);% 频域图像乘以滤波器的系数
end
end
%real函数取元素的实部
J=real(ifft2(ifftshift(J)));% 时域图像
subplot(142),imshow(J,[]);title('理想低通滤波所得图像');
%将巴特沃斯高通滤波器
K=fftshift(fft2(im2double(img)));
[N1,N2]=size(K);%求二维傅里叶变换后图像大小
n=1;n1=round(N1/2);n2=round(N2/2);
d0=30; % 阶数n截止频率
for i=1:N1 %双重for循环计算频率点(i,j)与频域中心的距离
for j=1:N2
distance=sqrt((i-n1)^2+(j-n2)^2);
if distance==0
h=0;
else
h=1/(1+(distance/d0)^(2*n));% 根据巴特沃斯高通滤波器公式为1/(1+[D0/D(i,j)]^2n)
end
K(i,j)=h*K(i,j);% 频域图像乘以滤波器的系数
end
end
% real函数取元素的实部
K=real(ifft2(ifftshift(K)));% 时域图像
subplot(143),imshow(K,[]);title('Butterworth低通滤波图像');
% 高斯低通滤波器
L=fftshift(fft2(im2double(img)));
[a,b]=size(L);a0=round(a/2);b0=round(b/2);
d0=30; % 截止频率D0设置为30
for i=1:a
for j=1:b
distance=sqrt((i-a0)^2+(j-b0)^2); % 公式H(u,v)=e^-[D^2(u,v)/2*D0^2]
h=(exp(-(distance^2)/(2*(d0^2))));
L(i,j)=h*L(i,j);% 频域图像乘以滤波器的系数
end
end
L=real(ifft2(ifftshift(L)));% 转换为时域图像
subplot(144),imshow(L,[]); title('高斯低通滤波图像');3、图像分析
理想低通滤波：
保留图像中的低频分量而除去高频分量。所以低通滤波可以除去或削弱噪声的影响并模糊边缘轮廓。
可以看到随着截止频率的增大，保留的信息越来越多，故图像也愈发清晰，细节更加明显。可以观察到较为明显的振铃效应，这是由于理想低通滤波器本身的特性导致的，无法随着频率改变而彻底消除。
巴特沃斯低通滤波：
可以看出，当截止频率较低时，高频细节会被更严格地抑制，使图像变得更加模糊和平滑。当截止频率较高时，滤波器会通过更多的高频信息，从而保留图像中的细节和纹理，但在图中还是能够发现一些振铃现象的存在。
高斯低通滤波：
可以看出截止频率较低:高频分量被更强烈地抑制，图像会更加模糊，丧失一些细节。截止频率较高:如果截止频率较高，滤波器主要保留图像的大部分频率分量，得到的图像和原图更相像。使用较高的截止频率可以突出图像的边缘和纹理以及处理后的图像不会产生振铃效应。