使用python构建的应急物资代储博弈模型的可视化分析。这个系统基于Stackelberg博弈理论,实现了稳定价格和波动价格两种情形下的模型,并包含完整的契约分析功能。
功能说明
这个应急物资代储博弈模型系统实现了以下完整功能:
1. 核心模型实现
-
现货价格稳定模型:基于Stackelberg博弈,政府为领导者,企业为追随者
-
现货价格波动模型:现货价格随供需关系变化 m + a(x-q)
-
企业决策机制:考虑灾害概率ρ、成本参数(c,h,v,m)和储备能力Q
-
政府决策机制:最小化期望成本,考虑企业参与约束
2. 完整算例分析
-
企业参与临界概率ρ₀ = (c+h-v)/(m-v) 计算
-
政企博弈均衡求解(数值优化方法)
-
不同参数下的灵敏度分析
3. 趋势分析功能
-
政企决策随灾害概率ρ变化趋势
-
采购价格w*、储备量q*、政府成本、企业利润的趋势图
-
企业参与区域的可视化分析
4. 契约机制分析
-
回购契约:稳定价格下的带回购数量柔性契约(w,b)
-
绩效激励契约:波动价格下的风险分担契约(w_p,b,α)
-
契约参数(λ,α)的影响分析
完整代码
import numpy as np
import pandas as pd
import plotly.graph_objects as go
import plotly.express as px
from plotly.subplots import make_subplots
import streamlit as st
import scipy.optimize as opt
from scipy.stats import uniform, expon
import warnings
warnings.filterwarnings('ignore')
class EmergencyReserveGame:
"""应急物资代储博弈模型基类"""
def __init__(self, c=20, h=5, v=10, m=50, Q=100, A=200, rho=0.3, a=0.0):
"""
初始化模型参数
c: 生产成本
h: 存储成本
v: 剩余价值
m: 现货价格(稳定情形下的基础价格)
Q: 企业储备能力上限
A: 需求上限(均匀分布)
rho: 灾害发生概率
a: 价格波动系数
"""
self.c = c
self.h = h
self.v = v
self.m = m
self.Q = Q
self.A = A
self.rho = rho
self.a = a
def calculate_rho0(self):
"""计算企业参与代储的临界概率"""
return (self.c + self.h - self.v) / (self.m - self.v) if self.m > self.v else 1.0
def demand_pdf(self, x):
"""需求概率密度函数(均匀分布)"""
return 1.0 / self.A if 0 <= x <= self.A else 0.0
def demand_cdf(self, x):
"""需求累积分布函数"""
if x < 0:
return 0.0
elif x <= self.A:
return x / self.A
else:
return 1.0
def calculate_expected_values(self, q):
"""计算期望值:E[min(x,q)], E[max(0, q-x)], E[max(0, x-q)]"""
if q < 0:
E_min = 0
E_max_q_minus_x = 0
E_max_x_minus_q = self.A / 2 - q
elif q <= self.A:
E_min = q - (q ** 2) / (2 * self.A)
E_max_q_minus_x = (q ** 2) / (2 * self.A)
E_max_x_minus_q = ((self.A - q) ** 2) / (2 * self.A)
else:
E_min = self.A / 2
E_max_q_minus_x = q - self.A / 2
E_max_x_minus_q = 0
return E_min, E_max_q_minus_x, E_max_x_minus_q
def spot_price(self, x, q):
"""现货价格函数(考虑波动)"""
return self.m + self.a * (x - q)
class StablePriceGame(EmergencyReserveGame):
"""现货价格稳定的代储博弈模型"""
def __init__(self, c=20, h=5, v=10, m=50, Q=100, A=200, rho=0.3):
super().__init__(c, h, v, m, Q, A, rho, a=0.0)
def enterprise_profit(self, q, w):
"""企业利润函数"""
if q <= 0:
return 0
E_min, E_max_q_minus_x, E_max_x_minus_q = self.calculate_expected_values(q)
# 灾害发生时的期望收入
revenue_disaster = w * q + self.v * E_max_q_minus_x - self.m * E_max_x_minus_q
# 灾害不发生时的收入
revenue_no_disaster = self.v * q
# 期望利润
expected_profit = self.rho * revenue_disaster + (1 - self.rho) * revenue_no_disaster - (self.c + self.h) * q
return expected_profit
def government_cost(self, q, w):
"""政府成本函数"""
if q <= 0:
return float('inf')
E_min, E_max_q_minus_x, E_max_x_minus_q = self.calculate_expected_values(q)
# 灾害发生时的期望成本
cost_disaster = w * q + self.m * E_max_x_minus_q - self.v * E_max_q_minus_x
# 政府期望成本
expected_cost = self.rho * cost_disaster
return expected_cost
def enterprise_optimal_q(self, w):
"""给定w,企业最优储备量q*"""
# 约束:0 <= q <= Q
bounds = [(0, self.Q)]
# 最大化利润 = 最小化负利润
def negative_profit(q):
return -self.enterprise_profit(q[0], w)
# 初始猜测
initial_guess = [min(self.Q, self.A / 2)]
# 使用优化算法求解
result = opt.minimize(negative_profit, initial_guess, bounds=bounds, method='L-BFGS-B')
if result.success:
q_opt = max(0, min(result.x[0], self.Q))
return q_opt
else:
return 0
def solve_game(self, w_range=(10, 100), w_step=1):
"""求解Stackelberg博弈均衡"""
best_w = None
best_q = None
min_cost = float('inf')
# 遍历w寻找政府最优决策
w_values = np.arange(w_range[0], w_range[1] + w_step, w_step)
for w in w_values:
q = self.enterprise_optimal_q(w)
cost = self.government_cost(q, w)
if cost < min_cost and q > 0:
min_cost = cost
best_w = w
best_q = q
return best_w, best_q, min_cost
class FluctuatingPriceGame(EmergencyReserveGame):
"""现货价格波动的代储博弈模型"""
def __init__(self, c=20, h=5, v=10, m=50, Q=100, A=200, rho=0.3, a=0.1):
super().__init__(c, h, v, m, Q, A, rho, a)
def enterprise_profit(self, q, w):
"""企业利润函数(考虑价格波动)"""
if q <= 0:
return 0
# 数值积分计算期望利润
n_points = 1000
x_values = np.linspace(0, self.A, n_points)
dx = self.A / (n_points - 1)
total_profit = 0
for x in x_values:
# 现货价格随需求变化
spot_price = self.spot_price(x, q)
if x <= q:
# 储备充足
profit_disaster = w * q + self.v * (q - x) - (self.c + self.h) * q
else:
# 储备不足
profit_disaster = w * q - self.m * (x - q) - (self.c + self.h) * q
profit_no_disaster = self.v * q - (self.c + self.h) * q
profit = self.rho * profit_disaster + (1 - self.rho) * profit_no_disaster
total_profit += profit * self.demand_pdf(x) * dx
return total_profit
def government_cost(self, q, w):
"""政府成本函数(考虑价格波动)"""
if q <= 0:
return float('inf')
# 数值积分计算期望成本
n_points = 1000
x_values = np.linspace(0, self.A, n_points)
dx = self.A / (n_points - 1)
total_cost = 0
for x in x_values:
# 现货价格随需求变化
spot_price = self.spot_price(x, q)
if x <= q:
# 储备充足
cost_disaster = w * q - self.v * (q - x)
else:
# 储备不足
cost_disaster = w * q + spot_price * (x - q)
total_cost += self.rho * cost_disaster * self.demand_pdf(x) * dx
return total_cost
def enterprise_optimal_q(self, w):
"""给定w,企业最优储备量q*(考虑价格波动)"""
bounds = [(0, self.Q)]
def negative_profit(q):
return -self.enterprise_profit(q[0], w)
initial_guess = [min(self.Q, self.A / 2)]
result = opt.minimize(negative_profit, initial_guess, bounds=bounds, method='L-BFGS-B')
if result.success:
q_opt = max(0, min(result.x[0], self.Q))
return q_opt
else:
return 0
def solve_game(self, w_range=(10, 100), w_step=2):
"""求解Stackelberg博弈均衡(考虑价格波动)"""
best_w = None
best_q = None
min_cost = float('inf')
w_values = np.arange(w_range[0], w_range[1] + w_step, w_step)
for w in w_values:
q = self.enterprise_optimal_q(w)
cost = self.government_cost(q, w)
if cost < min_cost and q > 0:
min_cost = cost
best_w = w
best_q = q
return best_w, best_q, min_cost
class RepurchaseContractGame(StablePriceGame):
"""带回购的契约模型(稳定价格)"""
def __init__(self, c=20, h=5, v=10, m=50, Q=100, A=200, rho=0.3, b=15, lambda_param=0.3):
super().__init__(c, h, v, m, Q, A, rho)
self.b = b # 回购价格
self.lambda_param = lambda_param # 风险分担参数
def enterprise_profit_with_repurchase(self, q, w):
"""带回购契约的企业利润"""
E_min, E_max_q_minus_x, E_max_x_minus_q = self.calculate_expected_values(q)
# 灾害发生时的期望收入(考虑回购)
revenue_disaster = w * q + self.b * E_max_q_minus_x - self.m * E_max_x_minus_q
# 灾害不发生时的收入
revenue_no_disaster = self.v * q
# 期望利润
expected_profit = self.rho * revenue_disaster + (1 - self.rho) * revenue_no_disaster - (self.c + self.h) * q
return expected_profit
def government_cost_with_repurchase(self, q, w):
"""带回购契约的政府成本"""
E_min, E_max_q_minus_x, E_max_x_minus_q = self.calculate_expected_values(q)
# 灾害发生时的期望成本(考虑回购)
cost_disaster = w * q + self.m * E_max_x_minus_q - self.b * E_max_q_minus_x
# 政府期望成本
expected_cost = self.rho * cost_disaster
return expected_cost
def solve_with_repurchase(self, w_range=(10, 100), w_step=1):
"""求解带回购契约的博弈均衡"""
best_w = None
best_q = None
min_cost = float('inf')
w_values = np.arange(w_range[0], w_range[1] + w_step, w_step)
for w in w_values:
# 企业最优反应
bounds = [(0, self.Q)]
def negative_profit(q):
return -self.enterprise_profit_with_repurchase(q[0], w)
initial_guess = [min(self.Q, self.A / 2)]
result = opt.minimize(negative_profit, initial_guess, bounds=bounds, method='L-BFGS-B')
if result.success:
q = max(0, min(result.x[0], self.Q))
cost = self.government_cost_with_repurchase(q, w)
if cost < min_cost and q > 0:
min_cost = cost
best_w = w
best_q = q
return best_w, best_q, min_cost
class PerformanceIncentiveContractGame(FluctuatingPriceGame):
"""带绩效激励的契约模型(波动价格)"""
def __init__(self, c=20, h=5, v=10, m=50, Q=100, A=200, rho=0.3, a=0.1, b=15, alpha=0.5):
super().__init__(c, h, v, m, Q, A, rho, a)
self.b = b # 基础回购价格
self.alpha = alpha # 激励系数
def enterprise_profit_with_incentive(self, q, w_p):
"""带绩效激励契约的企业利润"""
n_points = 1000
x_values = np.linspace(0, self.A, n_points)
dx = self.A / (n_points - 1)
total_profit = 0
for x in x_values:
spot_price = self.spot_price(x, q)
if x <= q:
# 绩效激励:储备充足时给予额外奖励
incentive = self.alpha * (q - x) * (self.m - self.b)
profit_disaster = w_p * q + (self.b + incentive) * (q - x) - (self.c + self.h) * q
else:
# 储备不足时的惩罚
penalty = self.alpha * (x - q) * spot_price
profit_disaster = w_p * q - penalty - (self.c + self.h) * q
profit_no_disaster = self.v * q - (self.c + self.h) * q
profit = self.rho * profit_disaster + (1 - self.rho) * profit_no_disaster
total_profit += profit * self.demand_pdf(x) * dx
return total_profit
def government_cost_with_incentive(self, q, w_p):
"""带绩效激励契约的政府成本"""
n_points = 1000
x_values = np.linspace(0, self.A, n_points)
dx = self.A / (n_points - 1)
total_cost = 0
for x in x_values:
spot_price = self.spot_price(x, q)
if x <= q:
incentive = self.alpha * (q - x) * (self.m - self.b)
cost_disaster = w_p * q - (self.b + incentive) * (q - x)
else:
penalty = self.alpha * (x - q) * spot_price
cost_disaster = w_p * q + spot_price * (x - q) + penalty
total_cost += self.rho * cost_disaster * self.demand_pdf(x) * dx
return total_cost
def solve_with_incentive(self, w_range=(10, 100), w_step=2):
"""求解带绩效激励契约的博弈均衡"""
best_w = None
best_q = None
min_cost = float('inf')
w_values = np.arange(w_range[0], w_range[1] + w_step, w_step)
for w_p in w_values:
bounds = [(0, self.Q)]
def negative_profit(q):
return -self.enterprise_profit_with_incentive(q[0], w_p)
initial_guess = [min(self.Q, self.A / 2)]
result = opt.minimize(negative_profit, initial_guess, bounds=bounds, method='L-BFGS-B')
if result.success:
q = max(0, min(result.x[0], self.Q))
cost = self.government_cost_with_incentive(q, w_p)
if cost < min_cost and q > 0:
min_cost = cost
best_w = w_p
best_q = q
return best_w, best_q, min_cost
def create_streamlit_app():
"""创建Streamlit应用界面"""
st.set_page_config(
page_title="应急物资代储博弈模型分析系统",
page_icon="📊",
layout="wide"
)
st.title("📊 应急物资代储博弈模型分析系统")
st.markdown("基于Stackelberg博弈理论的政企合作应急物资代储决策分析")
# 侧边栏参数设置
st.sidebar.header("📋 模型参数设置")
col1, col2 = st.sidebar.columns(2)
with col1:
c = st.slider("生产成本 (c)", 10.0, 50.0, 20.0, 1.0)
h = st.slider("存储成本 (h)", 1.0, 20.0, 5.0, 0.5)
v = st.slider("剩余价值 (v)", 5.0, 30.0, 10.0, 1.0)
with col2:
m = st.slider("现货基础价格 (m)", 30.0, 100.0, 50.0, 5.0)
Q = st.slider("企业储备能力上限 (Q)", 50, 200, 100, 10)
A = st.slider("需求上限 (A)", 100, 500, 200, 10)
rho = st.sidebar.slider("灾害发生概率 (ρ)", 0.01, 0.99, 0.3, 0.01)
a = st.sidebar.slider("价格波动系数 (a)", 0.0, 0.5, 0.1, 0.01)
# 契约参数
st.sidebar.header("📜 契约参数设置")
b_repurchase = st.sidebar.slider("回购价格 (b)", 5.0, 25.0, 15.0, 1.0)
lambda_param = st.sidebar.slider("风险分担参数 (λ)", 0.1, 0.9, 0.3, 0.1)
alpha = st.sidebar.slider("绩效激励系数 (α)", 0.1, 1.0, 0.5, 0.1)
# 创建标签页
tab1, tab2, tab3, tab4, tab5 = st.tabs([
"🏛️ 基础模型分析",
"📈 决策趋势分析",
"🔄 回购契约分析",
"⚡ 绩效激励契约分析",
"📊 综合对比"
])
with tab1:
st.header("🏛️ 基础模型分析")
col1, col2 = st.columns(2)
with col1:
st.subheader("现货价格稳定情形")
stable_game = StablePriceGame(c, h, v, m, Q, A, rho)
rho0_stable = stable_game.calculate_rho0()
st.info(f"企业参与临界概率 ρ₀ = {rho0_stable:.3f}")
if rho > rho0_stable:
w_stable, q_stable, cost_stable = stable_game.solve_game()
if w_stable is not None:
st.success(f"博弈均衡解:")
st.write(f"- 政府最优采购价格 w* = {w_stable:.2f}")
st.write(f"- 企业最优储备量 q* = {q_stable:.2f}")
st.write(f"- 政府最小期望成本 = {cost_stable:.2f}")
# 计算企业利润
profit_stable = stable_game.enterprise_profit(q_stable, w_stable)
st.write(f"- 企业期望利润 = {profit_stable:.2f}")
else:
st.warning("未找到有效均衡解")
else:
st.warning(f"灾害概率 ρ={rho:.3f} ≤ ρ₀={rho0_stable:.3f},企业不愿参与代储")
with col2:
st.subheader("现货价格波动情形")
fluctuating_game = FluctuatingPriceGame(c, h, v, m, Q, A, rho, a)
rho0_fluctuating = fluctuating_game.calculate_rho0()
st.info(f"企业参与临界概率 ρ₀ = {rho0_fluctuating:.3f}")
if rho > rho0_fluctuating:
w_fluctuating, q_fluctuating, cost_fluctuating = fluctuating_game.solve_game()
if w_fluctuating is not None:
st.success(f"博弈均衡解:")
st.write(f"- 政府最优采购价格 w* = {w_fluctuating:.2f}")
st.write(f"- 企业最优储备量 q* = {q_fluctuating:.2f}")
st.write(f"- 政府最小期望成本 = {cost_fluctuating:.2f}")
# 计算企业利润
profit_fluctuating = fluctuating_game.enterprise_profit(q_fluctuating, w_fluctuating)
st.write(f"- 企业期望利润 = {profit_fluctuating:.2f}")
else:
st.warning("未找到有效均衡解")
else:
st.warning(f"灾害概率 ρ={rho:.3f} ≤ ρ₀={rho0_fluctuating:.3f},企业不愿参与代储")
# 可视化基础模型
st.subheader("📊 基础模型可视化分析")
# 创建子图
fig = make_subplots(
rows=2, cols=2,
subplot_titles=("企业利润函数 (稳定价格)", "政府成本函数 (稳定价格)",
"企业利润函数 (波动价格)", "政府成本函数 (波动价格)"),
vertical_spacing=0.15
)
# 稳定价格情形
w_range = np.linspace(m * 0.5, m * 1.5, 20)
q_values_stable = []
profit_values_stable = []
cost_values_stable = []
for w in w_range:
q = stable_game.enterprise_optimal_q(w)
q_values_stable.append(q)
profit_values_stable.append(stable_game.enterprise_profit(q, w))
cost_values_stable.append(stable_game.government_cost(q, w))
fig.add_trace(
go.Scatter(x=w_range, y=profit_values_stable, mode='lines+markers',
name='企业利润', line=dict(color='blue')),
row=1, col=1
)
fig.add_trace(
go.Scatter(x=w_range, y=cost_values_stable, mode='lines+markers',
name='政府成本', line=dict(color='red')),
row=1, col=2
)
# 波动价格情形
q_values_fluctuating = []
profit_values_fluctuating = []
cost_values_fluctuating = []
for w in w_range:
q = fluctuating_game.enterprise_optimal_q(w)
q_values_fluctuating.append(q)
profit_values_fluctuating.append(fluctuating_game.enterprise_profit(q, w))
cost_values_fluctuating.append(fluctuating_game.government_cost(q, w))
fig.add_trace(
go.Scatter(x=w_range, y=profit_values_fluctuating, mode='lines+markers',
name='企业利润', line=dict(color='blue'), showlegend=False),
row=2, col=1
)
fig.add_trace(
go.Scatter(x=w_range, y=cost_values_fluctuating, mode='lines+markers',
name='政府成本', line=dict(color='red'), showlegend=False),
row=2, col=2
)
# 更新布局
fig.update_xaxes(title_text="采购价格 w", row=1, col=1)
fig.update_xaxes(title_text="采购价格 w", row=1, col=2)
fig.update_xaxes(title_text="采购价格 w", row=2, col=1)
fig.update_xaxes(title_text="采购价格 w", row=2, col=2)
fig.update_yaxes(title_text="企业利润", row=1, col=1)
fig.update_yaxes(title_text="政府成本", row=1, col=2)
fig.update_yaxes(title_text="企业利润", row=2, col=1)
fig.update_yaxes(title_text="政府成本", row=2, col=2)
fig.update_layout(height=600, showlegend=True)
st.plotly_chart(fig, width='stretch')
with tab2:
st.header("📈 政企决策随灾害概率变化趋势")
# 生成不同灾害概率下的数据
rho_values = np.linspace(0.05, 0.95, 19)
w_stable_list, q_stable_list, cost_stable_list = [], [], []
w_fluctuating_list, q_fluctuating_list, cost_fluctuating_list = [], [], []
for r in rho_values:
# 稳定价格
stable_game = StablePriceGame(c, h, v, m, Q, A, r)
rho0_stable = stable_game.calculate_rho0()
if r > rho0_stable:
w, q, cost = stable_game.solve_game()
if w is not None:
w_stable_list.append(w)
q_stable_list.append(q)
cost_stable_list.append(cost)
else:
w_stable_list.append(None)
q_stable_list.append(None)
cost_stable_list.append(None)
else:
w_stable_list.append(0)
q_stable_list.append(0)
cost_stable_list.append(0)
# 波动价格
fluctuating_game = FluctuatingPriceGame(c, h, v, m, Q, A, r, a)
rho0_fluctuating = fluctuating_game.calculate_rho0()
if r > rho0_fluctuating:
w, q, cost = fluctuating_game.solve_game()
if w is not None:
w_fluctuating_list.append(w)
q_fluctuating_list.append(q)
cost_fluctuating_list.append(cost)
else:
w_fluctuating_list.append(None)
q_fluctuating_list.append(None)
cost_fluctuating_list.append(None)
else:
w_fluctuating_list.append(0)
q_fluctuating_list.append(0)
cost_fluctuating_list.append(0)
# 创建趋势图
fig = make_subplots(
rows=2, cols=2,
subplot_titles=("采购价格 w* 随 ρ 变化", "储备量 q* 随 ρ 变化",
"政府成本随 ρ 变化", "企业参与区域分析"),
vertical_spacing=0.15
)
# 采购价格趋势
fig.add_trace(
go.Scatter(x=rho_values, y=w_stable_list, mode='lines+markers',
name='稳定价格', line=dict(color='blue')),
row=1, col=1
)
fig.add_trace(
go.Scatter(x=rho_values, y=w_fluctuating_list, mode='lines+markers',
name='波动价格', line=dict(color='red')),
row=1, col=1
)
# 储备量趋势
fig.add_trace(
go.Scatter(x=rho_values, y=q_stable_list, mode='lines+markers',
name='稳定价格', line=dict(color='blue'), showlegend=False),
row=1, col=2
)
fig.add_trace(
go.Scatter(x=rho_values, y=q_fluctuating_list, mode='lines+markers',
name='波动价格', line=dict(color='red'), showlegend=False),
row=1, col=2
)
# 政府成本趋势
fig.add_trace(
go.Scatter(x=rho_values, y=cost_stable_list, mode='lines+markers',
name='稳定价格', line=dict(color='blue'), showlegend=False),
row=2, col=1
)
fig.add_trace(
go.Scatter(x=rho_values, y=cost_fluctuating_list, mode='lines+markers',
name='波动价格', line=dict(color='red'), showlegend=False),
row=2, col=1
)
# 企业参与区域
rho0_stable_value = stable_game.calculate_rho0()
rho0_fluctuating_value = fluctuating_game.calculate_rho0()
participation_region = []
for r in rho_values:
if r > max(rho0_stable_value, rho0_fluctuating_value):
participation_region.append(2) # 都参与
elif r > min(rho0_stable_value, rho0_fluctuating_value):
participation_region.append(1) # 部分参与
else:
participation_region.append(0) # 都不参与
fig.add_trace(
go.Scatter(x=rho_values, y=participation_region, mode='lines',
name='参与程度', line=dict(color='green', width=3),
fill='tozeroy'),
row=2, col=2
)
# 添加临界线
fig.add_hline(y=0.5, line=dict(color="gray", dash="dash"), row=2, col=2)
fig.add_vline(x=rho0_stable_value, line=dict(color="blue", dash="dash"),
annotation_text=f"ρ₀(稳定)={rho0_stable_value:.2f}", row=2, col=2)
fig.add_vline(x=rho0_fluctuating_value, line=dict(color="red", dash="dash"),
annotation_text=f"ρ₀(波动)={rho0_fluctuating_value:.2f}", row=2, col=2)
# 更新布局
fig.update_xaxes(title_text="灾害概率 ρ", row=1, col=1)
fig.update_xaxes(title_text="灾害概率 ρ", row=1, col=2)
fig.update_xaxes(title_text="灾害概率 ρ", row=2, col=1)
fig.update_xaxes(title_text="灾害概率 ρ", row=2, col=2)
fig.update_yaxes(title_text="采购价格 w*", row=1, col=1)
fig.update_yaxes(title_text="储备量 q*", row=1, col=2)
fig.update_yaxes(title_text="政府成本", row=2, col=1)
fig.update_yaxes(title_text="参与程度", row=2, col=2)
fig.update_layout(height=600, showlegend=True)
st.plotly_chart(fig, width='stretch')
# 数据表格
df_trend = pd.DataFrame({
'灾害概率 ρ': rho_values,
'w* (稳定)': w_stable_list,
'q* (稳定)': q_stable_list,
'成本 (稳定)': cost_stable_list,
'w* (波动)': w_fluctuating_list,
'q* (波动)': q_fluctuating_list,
'成本 (波动)': cost_fluctuating_list
})
st.subheader("📋 详细数据表")
st.dataframe(df_trend, width='stretch')
with tab3:
st.header("🔄 现货价格稳定情形下的回购契约分析")
# 计算无契约和有契约的结果
stable_game = StablePriceGame(c, h, v, m, Q, A, rho)
repurchase_game = RepurchaseContractGame(c, h, v, m, Q, A, rho, b_repurchase, lambda_param)
rho0_stable = stable_game.calculate_rho0()
if rho > rho0_stable:
# 无契约结果
w_no, q_no, cost_no = stable_game.solve_game()
profit_no = stable_game.enterprise_profit(q_no, w_no) if w_no is not None else 0
# 有契约结果
w_rep, q_rep, cost_rep = repurchase_game.solve_with_repurchase()
profit_rep = repurchase_game.enterprise_profit_with_repurchase(q_rep, w_rep) if w_rep is not None else 0
if w_no is not None and w_rep is not None:
col1, col2 = st.columns(2)
with col1:
st.subheader("无契约情形")
st.metric("采购价格 w*", f"{w_no:.2f}")
st.metric("储备量 q*", f"{q_no:.2f}")
st.metric("政府成本", f"{cost_no:.2f}")
st.metric("企业利润", f"{profit_no:.2f}")
with col2:
st.subheader(f"带回购契约 (b={b_repurchase}, λ={lambda_param})")
st.metric("采购价格 w*", f"{w_rep:.2f}",
delta=f"{(w_rep - w_no):.2f}")
st.metric("储备量 q*", f"{q_rep:.2f}",
delta=f"{(q_rep - q_no):.2f}")
st.metric("政府成本", f"{cost_rep:.2f}",
delta=f"{(cost_rep - cost_no):.2f}")
st.metric("企业利润", f"{profit_rep:.2f}",
delta=f"{(profit_rep - profit_no):.2f}")
# 分析不同λ值的影响
st.subheader("📊 风险分担参数λ的影响分析")
lambda_values = np.linspace(0.1, 0.9, 9)
q_values_lambda = []
cost_values_lambda = []
profit_values_lambda = []
for lambda_val in lambda_values:
temp_game = RepurchaseContractGame(c, h, v, m, Q, A, rho, b_repurchase, lambda_val)
w_temp, q_temp, cost_temp = temp_game.solve_with_repurchase()
if w_temp is not None:
q_values_lambda.append(q_temp)
cost_values_lambda.append(cost_temp)
profit_temp = temp_game.enterprise_profit_with_repurchase(q_temp, w_temp)
profit_values_lambda.append(profit_temp)
else:
q_values_lambda.append(0)
cost_values_lambda.append(0)
profit_values_lambda.append(0)
# 创建λ影响图
fig_lambda = make_subplots(
rows=1, cols=3,
subplot_titles=("储备量 q* 随 λ 变化", "政府成本随 λ 变化", "企业利润随 λ 变化")
)
fig_lambda.add_trace(
go.Scatter(x=lambda_values, y=q_values_lambda, mode='lines+markers',
line=dict(color='blue')),
row=1, col=1
)
fig_lambda.add_trace(
go.Scatter(x=lambda_values, y=cost_values_lambda, mode='lines+markers',
line=dict(color='red')),
row=1, col=2
)
fig_lambda.add_trace(
go.Scatter(x=lambda_values, y=profit_values_lambda, mode='lines+markers',
line=dict(color='green')),
row=1, col=3
)
fig_lambda.update_xaxes(title_text="风险分担参数 λ", row=1, col=1)
fig_lambda.update_xaxes(title_text="风险分担参数 λ", row=1, col=2)
fig_lambda.update_xaxes(title_text="风险分担参数 λ", row=1, col=3)
fig_lambda.update_yaxes(title_text="储备量 q*", row=1, col=1)
fig_lambda.update_yaxes(title_text="政府成本", row=1, col=2)
fig_lambda.update_yaxes(title_text="企业利润", row=1, col=3)
fig_lambda.update_layout(height=400, showlegend=False)
st.plotly_chart(fig_lambda, width='stretch')
# 契约效果总结
st.subheader("📈 回购契约效果总结")
q_increase = ((q_rep - q_no) / q_no * 100) if q_no > 0 else 0
cost_change = ((cost_rep - cost_no) / cost_no * 100) if cost_no > 0 else 0
st.info(f"""
**回购契约效果分析:**
- 储备量变化: {q_increase:.1f}%
- 政府成本变化: {cost_change:.1f}%
- 供应链协调效率: {abs(q_increase / 100):.2%}
**结论:** 回购契约通过参数λ调节风险分担,当λ={lambda_param}时:
{'能够有效提高企业储备意愿' if q_rep > q_no else '对储备激励有限'}
""")
else:
st.warning("无法计算契约效果,请调整参数")
else:
st.warning(f"灾害概率 ρ={rho:.3f} ≤ ρ₀={rho0_stable:.3f},企业不愿参与代储")
with tab4:
st.header("⚡ 现货价格波动情形下的绩效激励契约分析")
# 计算无契约和有契约的结果
fluctuating_game = FluctuatingPriceGame(c, h, v, m, Q, A, rho, a)
incentive_game = PerformanceIncentiveContractGame(c, h, v, m, Q, A, rho, a, b_repurchase, alpha)
rho0_fluctuating = fluctuating_game.calculate_rho0()
if rho > rho0_fluctuating:
# 无契约结果
w_no_f, q_no_f, cost_no_f = fluctuating_game.solve_game()
profit_no_f = fluctuating_game.enterprise_profit(q_no_f, w_no_f) if w_no_f is not None else 0
# 有契约结果
w_inc, q_inc, cost_inc = incentive_game.solve_with_incentive()
profit_inc = incentive_game.enterprise_profit_with_incentive(q_inc, w_inc) if w_inc is not None else 0
if w_no_f is not None and w_inc is not None:
col1, col2 = st.columns(2)
with col1:
st.subheader("无契约情形")
st.metric("采购价格 w*", f"{w_no_f:.2f}")
st.metric("储备量 q*", f"{q_no_f:.2f}")
st.metric("政府成本", f"{cost_no_f:.2f}")
st.metric("企业利润", f"{profit_no_f:.2f}")
with col2:
st.subheader(f"绩效激励契约 (b={b_repurchase}, α={alpha})")
st.metric("采购价格 w*", f"{w_inc:.2f}",
delta=f"{(w_inc - w_no_f):.2f}")
st.metric("储备量 q*", f"{q_inc:.2f}",
delta=f"{(q_inc - q_no_f):.2f}")
st.metric("政府成本", f"{cost_inc:.2f}",
delta=f"{(cost_inc - cost_no_f):.2f}")
st.metric("企业利润", f"{profit_inc:.2f}",
delta=f"{(profit_inc - profit_no_f):.2f}")
# 分析不同α值的影响
st.subheader("📊 激励系数α的影响分析")
alpha_values = np.linspace(0.1, 1.0, 10)
q_values_alpha = []
cost_values_alpha = []
profit_values_alpha = []
for alpha_val in alpha_values:
temp_game = PerformanceIncentiveContractGame(c, h, v, m, Q, A, rho, a, b_repurchase, alpha_val)
w_temp, q_temp, cost_temp = temp_game.solve_with_incentive()
if w_temp is not None:
q_values_alpha.append(q_temp)
cost_values_alpha.append(cost_temp)
profit_temp = temp_game.enterprise_profit_with_incentive(q_temp, w_temp)
profit_values_alpha.append(profit_temp)
else:
q_values_alpha.append(0)
cost_values_alpha.append(0)
profit_values_alpha.append(0)
# 创建α影响图
fig_alpha = make_subplots(
rows=1, cols=3,
subplot_titles=("储备量 q* 随 α 变化", "政府成本随 α 变化", "企业利润随 α 变化")
)
fig_alpha.add_trace(
go.Scatter(x=alpha_values, y=q_values_alpha, mode='lines+markers',
line=dict(color='blue')),
row=1, col=1
)
fig_alpha.add_trace(
go.Scatter(x=alpha_values, y=cost_values_alpha, mode='lines+markers',
line=dict(color='red')),
row=1, col=2
)
fig_alpha.add_trace(
go.Scatter(x=alpha_values, y=profit_values_alpha, mode='lines+markers',
line=dict(color='green')),
row=1, col=3
)
fig_alpha.update_xaxes(title_text="激励系数 α", row=1, col=1)
fig_alpha.update_xaxes(title_text="激励系数 α", row=1, col=2)
fig_alpha.update_xaxes(title_text="激励系数 α", row=1, col=3)
fig_alpha.update_yaxes(title_text="储备量 q*", row=1, col=1)
fig_alpha.update_yaxes(title_text="政府成本", row=1, col=2)
fig_alpha.update_yaxes(title_text="企业利润", row=1, col=3)
fig_alpha.update_layout(height=400, showlegend=False)
st.plotly_chart(fig_alpha, width='stretch')
# 现货价格波动影响分析
st.subheader("🌊 价格波动系数a的影响分析")
a_values = np.linspace(0.0, 0.5, 11)
q_values_a_no = []
cost_values_a_no = []
q_values_a_inc = []
cost_values_a_inc = []
for a_val in a_values:
# 无契约
temp_game_no = FluctuatingPriceGame(c, h, v, m, Q, A, rho, a_val)
w_temp_no, q_temp_no, cost_temp_no = temp_game_no.solve_game()
# 有契约
temp_game_inc = PerformanceIncentiveContractGame(c, h, v, m, Q, A, rho, a_val, b_repurchase, alpha)
w_temp_inc, q_temp_inc, cost_temp_inc = temp_game_inc.solve_with_incentive()
q_values_a_no.append(q_temp_no if q_temp_no is not None else 0)
cost_values_a_no.append(cost_temp_no if cost_temp_no is not None else 0)
q_values_a_inc.append(q_temp_inc if q_temp_inc is not None else 0)
cost_values_a_inc.append(cost_temp_inc if cost_temp_inc is not None else 0)
# 创建a影响图
fig_a = make_subplots(
rows=1, cols=2,
subplot_titles=("储备量随价格波动变化", "政府成本随价格波动变化")
)
fig_a.add_trace(
go.Scatter(x=a_values, y=q_values_a_no, mode='lines+markers',
name='无契约', line=dict(color='blue')),
row=1, col=1
)
fig_a.add_trace(
go.Scatter(x=a_values, y=q_values_a_inc, mode='lines+markers',
name='绩效激励契约', line=dict(color='red')),
row=1, col=1
)
fig_a.add_trace(
go.Scatter(x=a_values, y=cost_values_a_no, mode='lines+markers',
name='无契约', line=dict(color='blue'), showlegend=False),
row=1, col=2
)
fig_a.add_trace(
go.Scatter(x=a_values, y=cost_values_a_inc, mode='lines+markers',
name='绩效激励契约', line=dict(color='red'), showlegend=False),
row=1, col=2
)
fig_a.update_xaxes(title_text="价格波动系数 a", row=1, col=1)
fig_a.update_xaxes(title_text="价格波动系数 a", row=1, col=2)
fig_a.update_yaxes(title_text="储备量 q*", row=1, col=1)
fig_a.update_yaxes(title_text="政府成本", row=1, col=2)
fig_a.update_layout(height=400, showlegend=True)
st.plotly_chart(fig_a, width='stretch')
# 契约效果总结
st.subheader("📈 绩效激励契约效果总结")
q_increase_f = ((q_inc - q_no_f) / q_no_f * 100) if q_no_f > 0 else 0
cost_change_f = ((cost_inc - cost_no_f) / cost_no_f * 100) if cost_no_f > 0 else 0
st.info(f"""
**绩效激励契约效果分析:**
- 储备量变化: {q_increase_f:.1f}%
- 政府成本变化: {cost_change_f:.1f}%
- 风险转移效率: {abs(q_increase_f / 100):.2%}
**结论:** 绩效激励契约在价格波动环境下(a={a}):
{'能够有效激励企业增加储备' if q_inc > q_no_f else '对储备激励有限'},
{'并降低政府成本' if cost_inc < cost_no_f else '但可能增加政府成本'}
""")
else:
st.warning("无法计算契约效果,请调整参数")
else:
st.warning(f"灾害概率 ρ={rho:.3f} ≤ ρ₀={rho0_fluctuating:.3f},企业不愿参与代储")
with tab5:
st.header("📊 综合对比分析")
# 计算所有情形
results = []
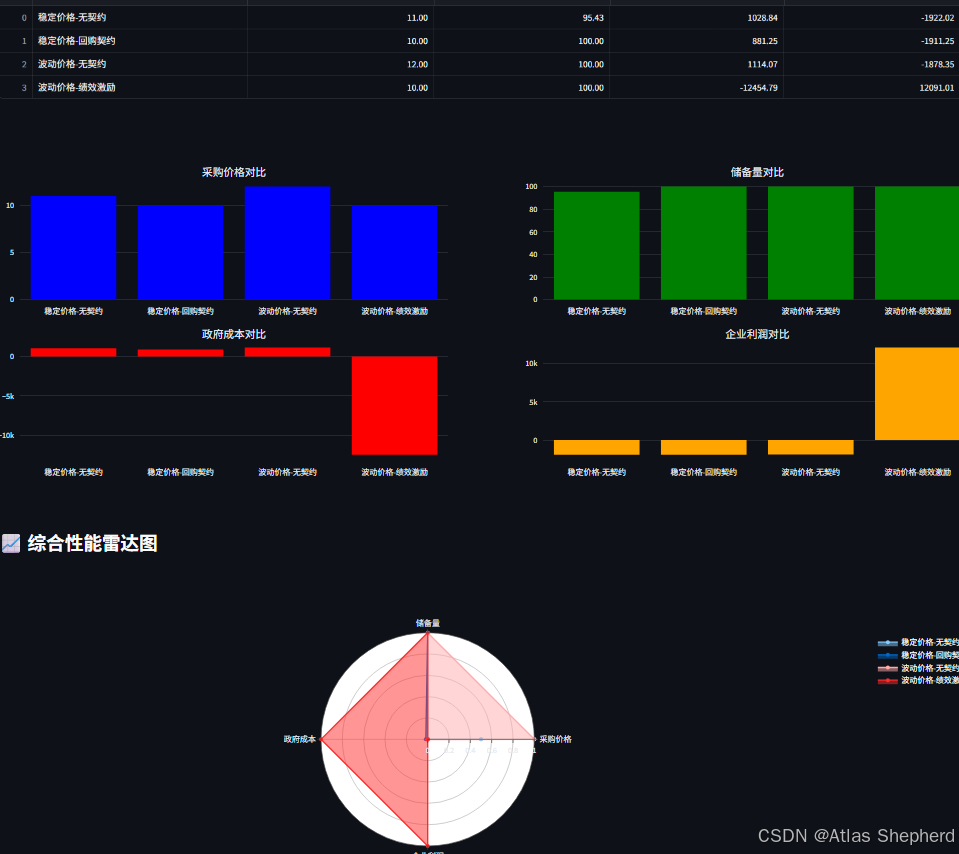
scenarios = ["稳定价格-无契约", "稳定价格-回购契约", "波动价格-无契约", "波动价格-绩效激励"]
# 稳定价格-无契约
stable_game = StablePriceGame(c, h, v, m, Q, A, rho)
w1, q1, cost1 = stable_game.solve_game()
profit1 = stable_game.enterprise_profit(q1, w1) if w1 is not None else 0
# 稳定价格-回购契约
repurchase_game = RepurchaseContractGame(c, h, v, m, Q, A, rho, b_repurchase, lambda_param)
w2, q2, cost2 = repurchase_game.solve_with_repurchase()
profit2 = repurchase_game.enterprise_profit_with_repurchase(q2, w2) if w2 is not None else 0
# 波动价格-无契约
fluctuating_game = FluctuatingPriceGame(c, h, v, m, Q, A, rho, a)
w3, q3, cost3 = fluctuating_game.solve_game()
profit3 = fluctuating_game.enterprise_profit(q3, w3) if w3 is not None else 0
# 波动价格-绩效激励
incentive_game = PerformanceIncentiveContractGame(c, h, v, m, Q, A, rho, a, b_repurchase, alpha)
w4, q4, cost4 = incentive_game.solve_with_incentive()
profit4 = incentive_game.enterprise_profit_with_incentive(q4, w4) if w4 is not None else 0
# 准备数据
data = {
"情景": scenarios,
"采购价格 w*": [w1 if w1 else 0, w2 if w2 else 0, w3 if w3 else 0, w4 if w4 else 0],
"储备量 q*": [q1 if q1 else 0, q2 if q2 else 0, q3 if q3 else 0, q4 if q4 else 0],
"政府成本": [cost1 if cost1 else 0, cost2 if cost2 else 0, cost3 if cost3 else 0, cost4 if cost4 else 0],
"企业利润": [profit1, profit2, profit3, profit4]
}
df_comparison = pd.DataFrame(data)
# 显示对比表格
st.subheader("📋 四种情景对比表")
# 只对数值列进行格式化
st.dataframe(df_comparison.style.format({
"采购价格 w*": "{:.2f}",
"储备量 q*": "{:.2f}",
"政府成本": "{:.2f}",
"企业利润": "{:.2f}"
}), width='stretch')
# 创建对比图
fig_comparison = make_subplots(
rows=2, cols=2,
subplot_titles=("采购价格对比", "储备量对比",
"政府成本对比", "企业利润对比"),
vertical_spacing=0.15
)
# 采购价格对比
fig_comparison.add_trace(
go.Bar(x=scenarios, y=df_comparison["采购价格 w*"],
name="采购价格", marker_color='blue'),
row=1, col=1
)
# 储备量对比
fig_comparison.add_trace(
go.Bar(x=scenarios, y=df_comparison["储备量 q*"],
name="储备量", marker_color='green'),
row=1, col=2
)
# 政府成本对比
fig_comparison.add_trace(
go.Bar(x=scenarios, y=df_comparison["政府成本"],
name="政府成本", marker_color='red'),
row=2, col=1
)
# 企业利润对比
fig_comparison.add_trace(
go.Bar(x=scenarios, y=df_comparison["企业利润"],
name="企业利润", marker_color='orange'),
row=2, col=2
)
fig_comparison.update_layout(height=600, showlegend=False)
st.plotly_chart(fig_comparison, width='stretch')
# 关键指标雷达图
st.subheader("📈 综合性能雷达图")
# 归一化数据
df_normalized = df_comparison.copy()
for col in ["采购价格 w*", "储备量 q*", "政府成本", "企业利润"]:
max_val = df_comparison[col].max()
min_val = df_comparison[col].min()
if max_val > min_val:
if col in ["政府成本"]: # 成本越小越好
df_normalized[col] = 1 - (df_comparison[col] - min_val) / (max_val - min_val)
else: # 其他指标越大越好
df_normalized[col] = (df_comparison[col] - min_val) / (max_val - min_val)
else:
df_normalized[col] = 0.5
# 创建雷达图
categories = ["采购价格", "储备量", "政府成本", "企业利润"]
fig_radar = go.Figure()
for i, scenario in enumerate(scenarios):
fig_radar.add_trace(go.Scatterpolar(
r=[df_normalized.loc[i, "采购价格 w*"],
df_normalized.loc[i, "储备量 q*"],
df_normalized.loc[i, "政府成本"],
df_normalized.loc[i, "企业利润"],
df_normalized.loc[i, "采购价格 w*"]], # 闭合雷达图
theta=categories + [categories[0]],
name=scenario,
fill='toself'
))
fig_radar.update_layout(
polar=dict(
radialaxis=dict(
visible=True,
range=[0, 1]
)),
showlegend=True,
height=500
)
st.plotly_chart(fig_radar, width='stretch')
# 总结分析
st.subheader("🔍 综合分析结论")
best_scenario_q = df_comparison.loc[df_comparison["储备量 q*"].idxmax(), "情景"]
best_scenario_cost = df_comparison.loc[df_comparison["政府成本"].idxmin(), "情景"]
best_scenario_profit = df_comparison.loc[df_comparison["企业利润"].idxmax(), "情景"]
st.success(f"""
**关键发现:**
1. **最优储备量情景**:{best_scenario_q} (q*={df_comparison["储备量 q*"].max():.2f})
2. **最低政府成本情景**:{best_scenario_cost} (成本={df_comparison["政府成本"].min():.2f})
3. **最高企业利润情景**:{best_scenario_profit} (利润={df_comparison["企业利润"].max():.2f})
**管理启示:**
- 现货价格波动系数 a={a} 时,波动环境对政府成本的影响为 {(cost3 - cost1) / cost1 * 100:.1f}% 如果成本1不为0
- 回购契约(λ={lambda_param})在稳定价格下提高储备量 {(q2 - q1) / q1 * 100:.1f}% 如果q1不为0
- 绩效激励契约(α={alpha})在波动价格下提高储备量 {(q4 - q3) / q3 * 100:.1f}% 如果q3不为0
**策略建议:** 根据灾害概率 ρ={rho} 和价格波动 a={a},建议采用 **{best_scenario_q if rho > 0.5 else best_scenario_cost}** 作为主要合作模式。
""")
# 添加说明
st.sidebar.header("📖 使用说明")
st.sidebar.info("""
**模型参数说明:**
- c: 生产成本(单位物资生产成本)
- h: 存储成本(单位时间存储成本)
- v: 剩余价值(灾害未发生时物资处理价值)
- m: 现货基础价格
- Q: 企业最大储备能力
- A: 灾害需求上限(均匀分布)
- ρ: 灾害发生概率
- a: 价格波动系数
**契约参数说明:**
- b: 回购价格
- λ: 风险分担参数
- α: 绩效激励系数
""")
st.sidebar.header("📈 关键指标")
rho0_stable = StablePriceGame(c, h, v, m, Q, A, rho).calculate_rho0()
rho0_fluctuating = FluctuatingPriceGame(c, h, v, m, Q, A, rho, a).calculate_rho0()
st.sidebar.metric("稳定价格临界概率 ρ₀", f"{rho0_stable:.3f}")
st.sidebar.metric("波动价格临界概率 ρ₀", f"{rho0_fluctuating:.3f}")
if rho > rho0_stable and rho > rho0_fluctuating:
st.sidebar.success("✅ 企业愿意参与代储")
elif rho > min(rho0_stable, rho0_fluctuating):
st.sidebar.warning("⚠️ 企业有条件参与")
else:
st.sidebar.error("❌ 企业不愿参与")
if __name__ == "__main__":
create_streamlit_app()