代码随想录算法训练营四十九天|图论part07

最小生成树之Prim

题目描述：

在世界的某个区域，有一些分散的神秘岛屿，每个岛屿上都有一种珍稀的资源或者宝藏。国王打算在这些岛屿上建公路，方便运输。

不同岛屿之间，路途距离不同，国王希望你可以规划建公路的方案，如何可以以最短的总公路距离将所有岛屿联通起来。

给定一张地图，其中包括了所有的岛屿，以及它们之间的距离。以最小化公路建设长度，确保可以链接到所有岛屿。

输入描述：

第一行包含两个整数V和E，V代表顶点数，E代表边数。顶点编号是从1到V。例如：V=2，一个有两个顶点，分别是1和2。

接下来共有E行，每行三个整数v1，v2和val，v1和v2为边的起点和终点，val代表边的权值。

输出描述：

输出联通所有岛屿的最小路径总距离

输入示例：

7 11

1 2 1

1 3 1

1 5 2

2 6 1

2 4 2

2 3 2

3 4 1

4 5 1

5 6 2

5 7 1

6 7 1

输出示例：

6

提示信息：

数据范围：

2 <= V <= 10000;

1 <= E <= 100000;

0 <= val <= 10000;

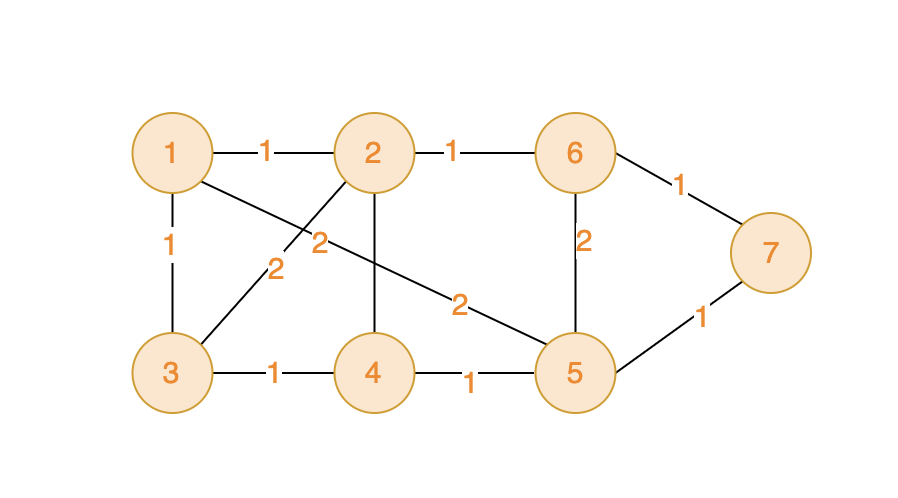
如下图，可见将所有的顶点都访问一遍，总距离最低是6.

Prim算法主要会用到一个minDist数组，这个数组记录所有非生成树节点距离生成树的最小距离。所以每添加一个节点到生成树中，就要看剩下的非生成树节点与该节点的距离是否小于原有的minDist值，如果小于，就需要更新minDist的值。

代码如下：

java 复制代码

import java.util.*;
 
public class Main{
    private static final int MAX=10001;
    private static int[] minDist;
    public static void main(String[] args){
        Scanner in=new Scanner(System.in);
        int v=in.nextInt();
        minDist=new int[v+1];
        for(int i=0;i<=v;i++){
            minDist[i]=MAX;
        }
        int e=in.nextInt();
        int[][] graph=new int[v+1][v+1];
        for(int i=0;i<=v;i++){
            for(int j=0;j<=v;j++){
                graph[i][j]=MAX;
            }
        }
        for(int i=0;i<e;i++){
            int v1=in.nextInt();
            int v2=in.nextInt();
            int val=in.nextInt();
            graph[v1][v2]=val;
            graph[v2][v1]=val;
        }
        boolean[] visited=new boolean[v+1];
        Prim(graph,minDist,visited);
        int result=0;
        for(int i=2;i<=v;i++){
            //System.out.println(minDist[i]);
            result+=minDist[i];
        }
        System.out.println(result);
    }
    public static void Prim(int[][] graph,int[] minDist,boolean[] visited){
        for(int i=1;i<graph.length-1;i++){
            int cur=-1;
            int minVal=Integer.MAX_VALUE;
            for(int j=1;j<=graph.length-1;j++){
                if(visited[j]==false&&minDist[j]<minVal){
                    minVal=minDist[j];
                    cur=j;
                }
            }
            visited[cur]=true;
            for(int j=1;j<=graph.length-1;j++){
                if(visited[j]==false&&graph[cur][j]<minDist[j]){
                    minDist[j]=graph[cur][j];
                }
            }
        }
    }
}

最小生成树之Kruskal

因为Kruscal算法是依次添加权值最小的边，所以每添加一条边就要看是否形成回路，也就是并查集的应用。

代码如下：

java 复制代码

import java.util.*;

class Edge{
    int x;
    int y;
    int val;

    public Edge(int x,int y,int val){
        this.x=x;
        this.y=y;
        this.val=val;
    }
}
public class Main{
    private static int[] father;
    private static List<Edge> edges=new ArrayList<>();
    public static void main(String[] args){
        Scanner in=new Scanner(System.in);
        int v=in.nextInt();
        father=new int[v+1];
        init(father);
        int e=in.nextInt();
        for(int i=0;i<e;i++){
            int x=in.nextInt();
            int y=in.nextInt();
            int val=in.nextInt();
            Edge edge=new Edge(x,y,val);
            edges.add(edge);
        }
        edges.sort((e1,e2)->Integer.compare(e1.val,e2.val));
        int res=0;
        for(Edge edge:edges){
            if(isSame(edge.x,edge.y))continue;
            join(edge.x,edge.y);
            res+=edge.val;
        }
        System.out.println(res);
    }
    public static void init(int[] father){
        for(int i=0;i<father.length;i++){
            father[i]=i;
        }
    }
    public static int find(int u){
        if(u==father[u])return u;
        else return father[u]=find(father[u]);
    }
    public static void join(int u,int v){
        u=find(u);
        v=find(v);
        if(u==v)return;
        father[v]=u;
    }
    public static boolean isSame(int u,int v){
        u=find(u);
        v=find(v);
        return u==v;
    }
}