深度学习——优化函数

在深度学习中，优化函数（Optimization Function）是指用于调整模型参数（如神经网络的权重和偏置），以最小化损失函数（Loss Function）的一类算法或方法。优化函数的目标是找到一组最优的参数，使得模型在训练数据上的预测结果与真实标签之间的差异最小。优化函数的选择直接影响模型的训练速度、收敛效果和最终性能。

一、优化问题的基本形式 在深度学习中，我们通常有一个损失函数 L(θ)，其中 θ 表示模型的参数（如权重）。优化的目标就是：

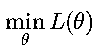
即通过不断调整参数 θ，使损失函数的值尽可能小。

这个优化问题可以进一步分解为：

1. 计算目标：找到使损失函数最小的参数组合
2. 优化方法：使用梯度信息指导参数更新方向
3. 终止条件：当损失函数收敛或达到最大迭代次数时停止

二、常见的优化函数（优化算法） 下面详细介绍几种最常用的深度学习优化算法，它们都是基于梯度下降（Gradient Descent）的思想，但在更新策略上有所不同，以提高训练效率、稳定性和收敛速度。

随机梯度下降（SGD, Stochastic Gradient Descent） 这是最基础的优化算法。

更新公式：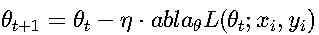

其中：

• η 是学习率（learning rate），通常取值在0.1到1e-5之间
• ∇_θ L 是损失函数关于参数的梯度
• 每次使用一个样本（或一个小批量）计算梯度

特点：

• 实现简单，计算开销小
• 参数更新方向波动较大
• 容易陷入局部极小值
• 学习率需要精心调整

应用场景：

• 小型数据集
• 简单的线性模型
• 作为其他优化算法的基准

小批量梯度下降（Mini-batch SGD） 实际应用中最常用，介于全批量梯度下降和随机梯度下降之间。

更新公式：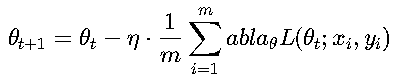

其中：

• m 是小批量大小（batch size），常用值为32、64、128等
• 计算小批量样本的平均梯度进行参数更新

特点：

• 平衡了计算效率和梯度稳定性
• 可以利用GPU的并行计算优势
• 仍然是许多高级优化算法的基础

带动量的SGD（Momentum SGD） 为了解决普通SGD更新方向震荡的问题，引入了"动量"的概念，累积之前的梯度信息。

更新公式：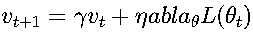

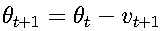
其中：

• v_t 是动量项（velocity），初始值为0
• γ 是动量系数，通常取0.9
• 相当于在参数更新时加入了惯性

优点：

• 加速收敛，特别是在损失函数曲面具有明显方向性的区域
• 减少参数更新过程中的震荡
• 有助于穿越平坦区域或局部极小值

Nesterov加速梯度（NAG, Nesterov Accelerated Gradient） 是Momentum的改进版，在计算梯度时"向前看一步"。

更新公式：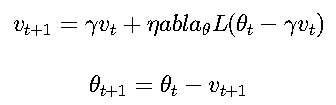

核心思想： 先根据当前动量走一步，再在这个"未来位置"计算梯度，更聪明地调整方向。

优点：

• 收敛速度比标准Momentum更快
• 在凸优化问题中能保证更好的理论收敛界
• 特别适合处理具有"峡谷"形状的损失函数曲面

AdaGrad（Adaptive Gradient） 为每个参数自适应地调整学习率，适合稀疏数据。

更新公式： G_t = G_{t-1} + (∇θ L)^2 θ{t+1} = θ_t - (η/√(G_t + ε))·∇_θ L

特点：

• 学习率随着时间递减
• 对频繁出现的参数使用较小的学习率
• 对不频繁出现的参数使用较大的学习率
• 缺点：学习率可能过早变得过小，导致训练停滞

RMSProp（Root Mean Square Propagation） 是对AdaGrad的改进，解决了学习率过快衰减的问题。

更新公式：

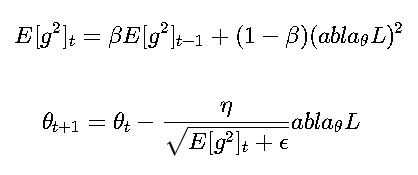
通常β=0.9

优点：

• 自适应学习率，适合非平稳目标
• 在实践中表现良好，尤其是RNN中
• 避免了AdaGrad的学习率过快衰减问题

Adam（Adaptive Moment Estimation）最流行 结合了动量（Momentum）和RMSProp的思想，是目前最常用的优化器之一。

更新公式：

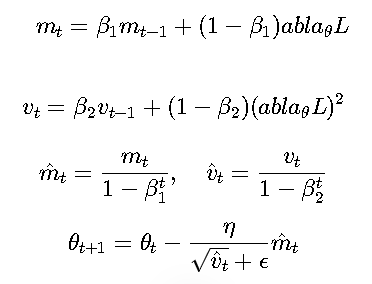
通常设置：

• β_1=0.9, β_2=0.999, ε=1e-8

优点：

• 收敛快，效果好，几乎适用于大部分任务
• 自适应学习率，对超参数相对鲁棒
• 同时考虑了梯度的一阶矩和二阶矩估计

AdamW 是对Adam的改进，主要解耦了权重衰减（weight decay）。

与Adam的区别：

• 在Adam中，权重衰减被混入梯度计算
• 在AdamW中，权重衰减单独处理 更新公式：

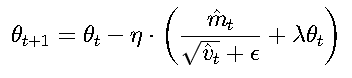
优点：

• 更符合权重衰减的原始定义
• 在大模型（如Transformer）中表现更好
• 训练过程更稳定

其他优化器（简要提及）

• Adadelta：不需要手动设置学习率
• SGD with Nesterov：带"前瞻"的动量法
• LAMB：用于大规模分布式训练
• RAdam：解决Adam初期训练不稳定的问题
• Lookahead、SWATS、NovoGrad等：较新或特定场景优化器

三、如何选择优化器？ 优化器选择指南：

对于新手或一般任务：

• 首选Adam或AdamW：这些自适应学习率优化器对大多数任务表现良好
• 默认参数通常就能获得不错效果：β1=0.9, β2=0.999, ε=1e-8
• 优势：自动调整各参数的学习率，减少调参工作量

对于需要精细调优的任务：

• 可以尝试SGD + Momentum：动量系数通常设为0.9
• 配合学习率调度器使用：如StepLR或ReduceLROnPlateau
• 优势：最终收敛效果可能更好，但需要更多调参经验

特定场景：

1. RNN/时序模型：

   • 推荐RMSProp
   • 原因：适合处理非平稳目标
   • 典型参数：ρ=0.9

2. 大模型训练：

   • AdamW或LAMB
   • 优势：正确处理权重衰减
   • 例如：BERT训练常用AdamW

3. 计算机视觉：

   • CNN：Adam
   • 传统方法：SGD
   • 例如：ResNet训练常用SGD

4. 强化学习：

   • RMSProp或Adam
   • 原因：适合随机性强的目标
   • 例如：DQN常用RMSProp

四、优化函数相关技巧

学习率（Learning Rate）

• 常用初始值：

  • 全连接网络：1e-3
  • CNN：1e-4
  • Transformer：1e-5

• 调度策略：

  1. Step Decay：
     • 示例：每30个epoch降低10倍
     • 适用：稳定收敛的任务
  2. Cosine Annealing：
     • 特点：平滑下降
     • 适用：图像分类
  3. One-cycle：
     • 特点：先升后降
     • 示例：最大学习率5e-3
     • 适用：快速训练

权重衰减（Weight Decay）

• 典型值：
  • 小模型：1e-4
  • 大模型：1e-2
• 注意事项：
  • 与学习率配合调整
  • AdamW中效果更好

梯度裁剪（Gradient Clipping）

• 阈值设置：
  • RNN：1.0
  • 其他：5.0
• 实现方式：
  • 按值裁剪
  • 按范数裁剪

热身（Warmup）

• 典型设置：
  • 前500-4000步
  • 线性增长
• 适用场景：
  • Transformer
  • 大batch训练

五、总结 关键要点：

优化目标：

• 最小化损失函数
• 找到最优参数组合
• 避免过拟合和欠拟合

算法选择：

1. Adam/AdamW：

   • 90%场景的首选
   • 示例：NLP任务

2. SGD+Momentum：

   • 需要更多调参
   • 示例：ImageNet训练

3. 特定架构：

   • RNN：RMSProp
   • GAN：通常Adam

调参技巧：

1. 学习率：

   • 初始值通过小实验确定
   • 使用LR Finder工具

2. 调度策略：

   • 根据验证集表现选择
   • 示例：plateau检测

3. 其他技巧：

   • 权重衰减：从1e-4开始尝试
   • 梯度裁剪：RNN必备

实践建议：

1. 训练流程：

   • 先用小数据测试
   • 监控loss/accuracy曲线
   • 早停策略

2. 工具利用：

   • TensorBoard监控
   • Optuna调参
   • 学习率探测器

3. 高级技巧：

   • 不同层不同学习率
   • 参数分组优化
   • 混合精度训练