这是我在我的网站中截取的文章,有更多的文章欢迎来访问我自己的博客网站rn.berlinlian.cn,这里还有很多有关计算机的知识,欢迎进行留言或者来我的网站进行留言!!!
一、引言
在数据分析、机器学习和信息检索中,"相似度(similarity)"与"距离(distance)"是帮助我们理解对象之间关系的核心概念。无论是比较两篇文档的相似程度、判断两个时间序列是否具有相同趋势,还是评估样本之间的差异,不同的相似度度量方法往往会得出完全不同的结论。
在众多方法中,Pearson 相关系数(Correlation) 、余弦相似度(Cosine Similarity) 和 **欧氏距离(Euclidean Distance)**是最常用的三类度量。它们的计算方式不同、关注的特征不同,在面对"缩放""平移"等变量变换时的表现也各不相同。因此,理解这三者的区别对于选择正确的工具至关重要。
本篇文章将系统比较 Correlation、Cosine Similarity 和 Euclidean Distance,从它们的性质、对变量变换的敏感性、在不同情境中的适用性等方面展开说明,并结合清晰的示例帮助读者掌握它们之间的本质区别。
**二、**三种度量方法的核心概念解析
在进行相似度或距离的计算时,我们最常见的三个度量方式就是 相关系数(Correlation) 、余弦相似度(Cosine Similarity) 和 欧氏距离(Euclidean Distance)。虽然它们听起来都像是在衡量"两个数据有多像",但本质上强调的方向完全不同。如果不了解它们的核心思想,在实际使用中就容易误判数据之间的关系。
为了建立清晰的理解,本章将围绕三个关键问题展开:
2.1 相关系数(Correlation)是什么?
相关系数主要关注的是两个变量的"变化趋势"是否一致 。
也就是说,当一个变量上升时,另一个变量是否也会上升;或者一个上升时另一个下降。
它 不关注变量的绝对大小,而关注变量"形状"的同步程度。
-
如果两个变量的波动 方向一致 → 相关系数接近 1
-
如果两个变量方向完全相反 → 接近 −1
-
如果完全没有线性关系 → 接近 0
换句话说,相关系数衡量的是 线性关系的强弱与方向。
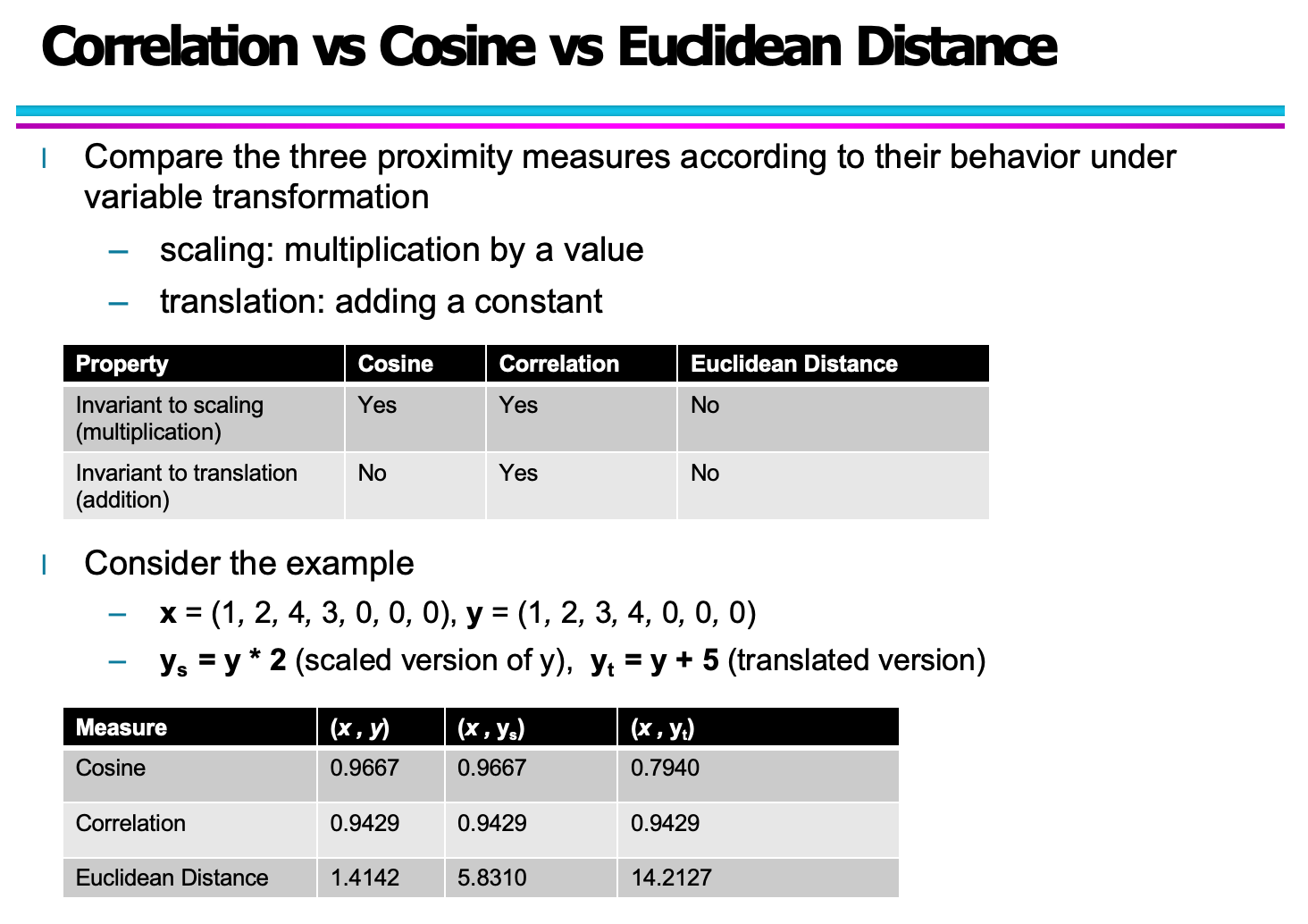
这张图展示了相关系数与缩放、平移之间的关系,并说明了相关系数对"加常数"与"乘常数"的不敏感性 ------ 正是因为它只关心变量的相对变化趋势。
2.2 余弦相似度(Cosine Similarity)是什么?
余弦相似度主要用于衡量两个向量的方向是否一致。
它不关心向量的长度,只关心两个向量所形成的夹角:
-
夹角小 → 方向一致 → 相似度高
-
夹角大 → 方向不一致 → 相似度低
这使得余弦相似度特别适用于 文本表示(如 TF-IDF 向量) :
文档的长度不同没关系,只要主题相似,余弦相似度就会反映出接近的结果。
2.3 欧氏距离(Euclidean Distance)是什么?
欧氏距离是我们最直观的距离概念:
它衡量的是 数据点之间的"绝对差异"。
假设我们把两个向量当成平面或空间中的坐标点,那么欧氏距离就表示这两个点之间的直线距离。
因此:
-
值越小 → 越相似
-
值越大 → 差异越明显
欧氏距离对 缩放 和 平移 都非常敏感:
数值大一点、偏移一点,都会影响结果。
这让它非常适合:
-
温度、坐标、测量值等"绝对量"比较
-
注重"数值差距"的场景
该图片中的表格已经清晰说明了欧氏距离在缩放与平移下的不稳定性。
2.4 小结:三者到底差在哪?
从数学含义到应用场景,这三者的核心差异可以总结为:
| 方法 | 关注点 | 是否关注大小? | 是否关注方向? | 是否关注趋势? |
|---|---|---|---|---|
| Correlation | 线性趋势 | 否 | 部分(通过线性变化体现) | ✔ 强烈关注 |
| Cosine Similarity | 向量方向 | 否 | ✔ 强烈关注 | 否 |
| Euclidean Distance | 数值差异 | ✔ 强烈关注 | 否 | 否 |
因此,选择哪一个取决于你想"比较"什么:
-
比较 趋势形状 → Correlation
-
比较 向量方向 → Cosine
-
比较 绝对差距 → Euclidean
**三、**案例比较分析
在理解了三种相似度/距离度量在缩放与平移上的性质之后,我们进一步通过示例来感受它们在实际数据上的表现差异。下面的例子使用了同一组向量 xx 与 yy,并构造了缩放版本 ysys 与平移版本 ytyt,从而对比三种度量方式的反应。
3.1 示例数据说明
我们使用如下数据集:
-
x=(1,2,4,3,0,0,0)
-
y=(1,2,3,4,0,0,0)
并构造:
-
缩放后的向量:ys=y×2
-
平移后的向量:yt=y+5
(在这里,缩放并不会改变变量之间的方向关系,而平移会整体移动数据。)

3.2 计算结果对比
三种度量对原始、缩放和平移后的版本的表现如下:
(1)余弦相似度(Cosine Similarity)
-
(x,y)=0.9667
-
(x,ys)=0.9667
-
(x,yt)=0.7940
余弦相似度在缩放后保持完全不变,因为缩放不会改变两个向量之间的角度。但在平移后,由于向量的方向发生变化,余弦相似度会下降。
(2)皮尔逊相关系数(Correlation)
-
(x,y)=0.9429
-
(x,ys)=0.9429
-
(x,yt)=0.9429
相关系数在缩放和平移后都完全保持不变,这体现了其 对线性结构(趋势)不对绝对大小敏感 的特性。
(3)欧氏距离(Euclidean Distance)
-
(x,y)=1.4142
-
(x,ys)=5.8310
-
(x,yt)=14.2127
欧氏距离对数值的变化极其敏感。缩放会放大两个向量之间的差异,平移更会导致整体偏移,从而让距离急剧增加。
3.3 结果解读
通过这个例子,我们可以看到不同度量方式关注的"相似性"并不相同:
✔ 余弦相似度:关注方向
如果两个向量的变化趋势相同(即在向量空间的方向一致),即使数值被放大,余弦相似度也不会变化。但一旦方向改变,如平移带来的偏移,余弦相似度就会显著下降。
✔ 相关系数:关注趋势(形状)
相关系数对缩放和平移都不敏感,只关注两个变量的线性关系是否一致。
换句话说,两个数据序列是否"同步变化"才是相关性最看重的。
✔ 欧氏距离:关注绝对差值
欧氏距离直接衡量两个向量在数值空间中的"物理距离",所以对任何数值变化都敏感。这使它特别适用于需要反映"差值本身"大小的场景,例如温度、长度或位置坐标。
**四、**不同场景下的度量选择指南
在实际应用中,选择哪一种相似度或距离度量,往往取决于数据的性质和任务目标。虽然相关系数、余弦相似度与欧氏距离都用于衡量对象之间的"相似"或"接近"程度,但它们关注的角度不同,因此适用的场景也不同。本章将结合典型案例,说明如何根据任务需求选择合适的衡量方式。


4.1 文本相似度:词频向量的比较(Cosine 更合适)
当比较文档时,我们通常会将文本表示为"词频向量"(如 TF、TF-IDF)。在这种情况下:
-
词向量的 方向 比 长度(大小) 更重要
-
不同文档可能长短不同,但关注的是"主题是否相似"
-
因此需要一个 忽略向量长度、关注方向关系 的度量
最合适的度量:余弦相似度(Cosine Similarity)
余弦相似度测量两个向量之间的"夹角",非常适合文档相似度分析。例如两个文本都大量使用了"machine"、"learning"、"model"等词,即使篇幅不同,它们的余弦相似度依然会很高。
4.2 绝对温度值的比较(Euclidean Distance 更合适)
当比较两个地点的温度(例如摄氏度)时,我们关心:
-
温度的 绝对差值
-
越接近越相似,偏差越大越不相似
-
不关注温度变化趋势,而关注"他们相差多少度"
最合适的度量:欧氏距离(Euclidean Distance)
欧氏距离直接计算两组数值之间的实际差异。在温度场景中,一个城市比另一个城市高 8°C,与高 2°C,相似度显然不同,欧氏距离能够准确反映这一点。
4.3 温度时间序列比较(Correlation 更合适)
如果关注的是:
-
两个时间序列的趋势是否相似
-
是否"同涨同跌"
-
是否在相同时间出现峰值与谷值
-
不关心温度的绝对大小差异
那么我们真正关心的是 变化的形状是否一致。
最合适的度量:相关系数(Correlation)
相关系数可以衡量两个时间序列的线性关系强弱,而不受以下因素影响:
-
平移(加上一常数)
-
缩放(乘以一常数)
例如,一个城市温度在 10--20°C 波动,另一个城市在 0--10°C 波动,但如果它们在同一时间点升降趋势一致,相关系数依然可以很高。
**五、**总结
在数据分析与机器学习中,Correlation(相关性) 、Cosine Similarity(余弦相似度) 、以及 Euclidean Distance(欧氏距离) 是最常见的三种相似性与差异性度量方法。虽然它们都用于判断两个对象之间的关系,但每种方法的关注点、数学含义和适合场景都有明显区别。
Correlation(相关性)关注的是变量之间的线性关系。它不关心数值的大小,只关心两个向量的变化是否一致。如果两个向量呈相同趋势上涨或下跌,那么相关性会很高;如果一个涨一个跌,相关性则为负。相关性度量的核心在于"方向是否一致",而不是"距离是否接近"。因此,它适用于时间序列分析、特征选择、用户行为趋势对比等需要关注变化趋势的场景。
Cosine Similarity(余弦相似度)则聚焦于两个向量之间的夹角,判断它们是否"朝向相似的方向"。即使两个向量的长度差异很大,只要它们的方向一致,余弦相似度也可以非常高。这让它非常适合文本分析、推荐系统、向量特征比较等高维场景。它的特点是"忽略大小,只看方向",尤其在稀疏向量中效果显著。
Euclidean Distance(欧氏距离)则完全不同,它关注的是两个点在空间中的绝对距离。它适合那些特征具有物理意义、且数值大小本身就是重要比较依据的场景,例如几何距离、图像像素差异、坐标点之间的距离等。欧氏距离强调"绝对差异",往往需要数据经过标准化或归一化处理,避免某些维度因为量纲过大而主导结果。
总体来看,这三种度量方式构成了判断向量关系的三种不同"视角":
-
相关性看"趋势关系是否一致";
-
余弦相似度看"方向是否一致";
-
欧氏距离看"差异是否接近"。
选择哪一种方法,不仅取决于数据本身的特性,也取决于你的分析目标。理解这三者的差异,能让我们在遇到实际问题时更准确地选择合适的工具,从而得到更合理、更可信的分析结果。
这是我在我的网站中截取的文章,有更多的文章欢迎来访问我自己的博客网站rn.berlinlian.cn,这里还有很多有关计算机的知识,欢迎进行留言或者来我的网站进行留言!!!