C语言做的量子计算模拟器

量子计算模拟器

一个用C语言实现的量子计算模拟器，支持基础量子门操作和量子态测量。

功能特性

核心功能

量子比特表示: 使用复数表示量子比特的叠加态
基础量子门: 实现Hadamard门、Pauli门（X、Y、Z）、CNOT门
量子态测量: 支持概率性测量和态坍缩
多量子比特系统: 支持多量子比特的纠缠态操作

线性代数应用

矩阵运算: 量子门表示为2x2幺正矩阵
向量操作: 量子态表示为复数向量
幺正性验证: 验证量子门的幺正性质

理论基础

量子比特

量子比特是量子计算的基本单位，可以表示为：

复制代码

|ψ⟩ = α|0⟩ + β|1⟩

其中 α 和 β 是复数，满足 |α|² + |β|² = 1。

量子门

量子门是作用在量子比特上的幺正变换：

Hadamard门

ini 复制代码

H = (1/√2) [1  1]
           [1 -1]

将计算基态转换为叠加态：

H|0⟩ = (|0⟩ + |1⟩)/√2
H|1⟩ = (|0⟩ - |1⟩)/√2

Pauli门

X门 (NOT门): X = [0 1; 1 0]
Y门: Y = [0 -i; i 0]
Z门: Z = [1 0; 0 -1]

CNOT门

控制非门，当控制比特为|1⟩时，翻转目标比特：

ini 复制代码

CNOT = [1 0 0 0]
       [0 1 0 0]
       [0 0 0 1]
       [0 0 1 0]

快速开始

环境要求

GCC编译器
C99标准支持
数学库 (libm)

快速编译和运行

bash 复制代码

# 1. 编译程序
gcc -Wall -std=c99 -O2 -lm main.c quantum_simulator.c -o quantum_simulator.exe

# 2. 运行程序
quantum_simulator.exe

编译和运行

编译

bash 复制代码

# 编译程序
gcc -Wall -std=c99 -O2 -lm main.c quantum_simulator.c -o quantum_simulator.exe

# 参数说明：
# -Wall: 启用所有警告
# -std=c99: 使用C99标准
# -O2: 优化级别2
# -lm: 链接数学库
# -o quantum_simulator.exe: 指定输出文件名

运行

bash 复制代码

# 运行程序
./quantum_simulator.exe

# Windows系统
quantum_simulator.exe

调试版本

bash 复制代码

# 编译调试版本
gcc -Wall -std=c99 -g -lm main.c quantum_simulator.c -o quantum_simulator_debug.exe

使用示例

单量子比特操作

c 复制代码

// 创建量子比特 |0⟩
Qubit q = create_qubit(1.0, 0.0);

// 应用Hadamard门
QuantumGate h = create_hadamard_gate();
q = apply_gate(q, h);

// 测量量子比特
double result = measure_qubit(q);

多量子比特系统

c 复制代码

// 创建2量子比特系统
QuantumSystem system = create_quantum_system(2);

// 初始化到 |00⟩ 状态
initialize_system(&system, 0);

// 应用量子门
QuantumGate h = create_hadamard_gate();
apply_single_qubit_gate(&system, 0, h);
apply_cnot_gate(&system, 0, 1);

// 测量系统
int result = measure_system(&system);

演示内容

程序包含以下演示：

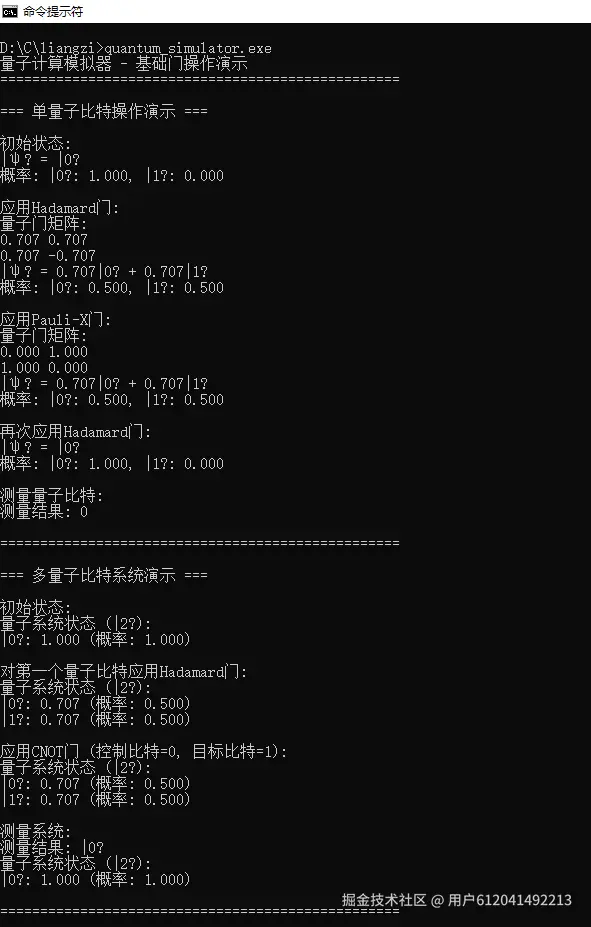
单量子比特操作: 展示Hadamard门和Pauli门的应用
多量子比特系统: 演示2量子比特系统的操作
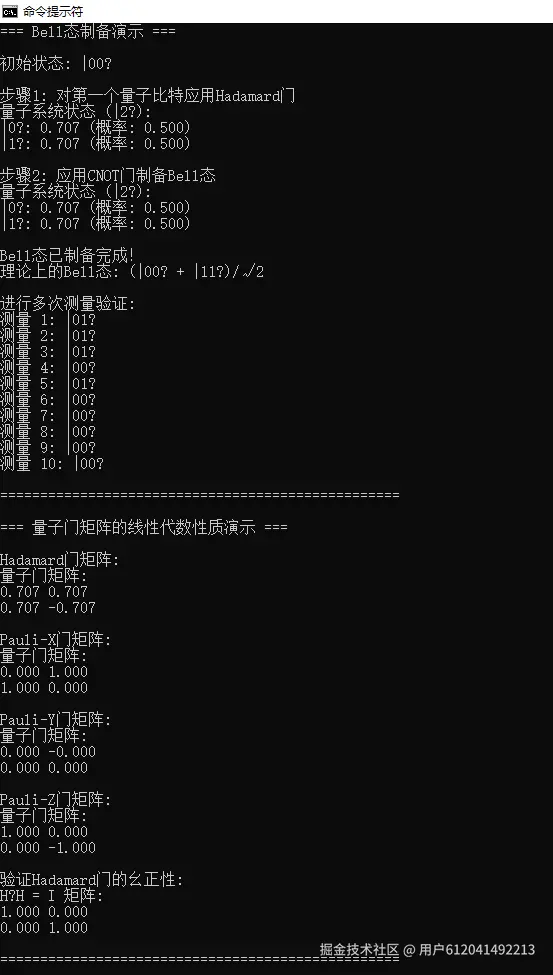
Bell态制备: 制备和验证Bell态 (|00⟩ + |11⟩)/√2
线性代数性质: 验证量子门的幺正性
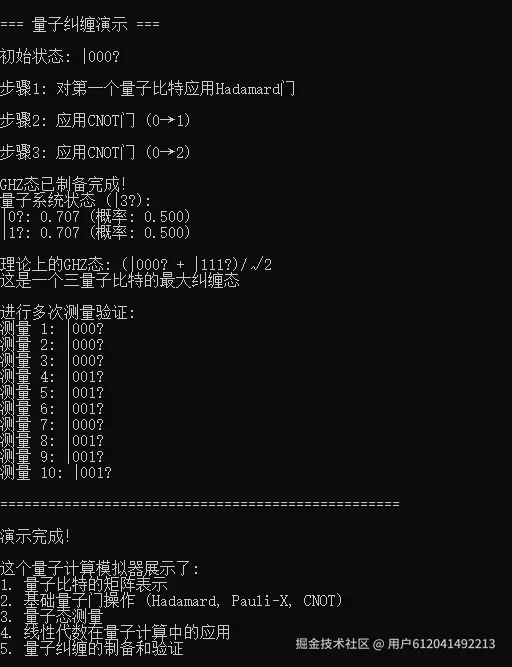
量子纠缠: 制备GHZ态并验证纠缠性质

项目结构

bash 复制代码

quantum_simulator/
├── quantum_simulator.h    # 头文件
├── quantum_simulator.c    # 核心实现
├── main.c                 # 主程序和演示
└── README.md             # 项目说明

数学背景

线性代数在量子计算中的应用

向量空间: 量子态生活在希尔伯特空间中
矩阵运算: 量子门是线性变换，用矩阵表示
幺正性: 量子门必须是幺正的，保持内积不变
张量积: 多量子比特系统通过张量积构造

测量理论

量子测量是概率性的，测量结果由Born规则决定：

测量|0⟩的概率: |α|²
测量|1⟩的概率: |β|²

扩展可能

实现更多量子门（旋转门、相位门等）
添加量子算法（Grover、Shor等）
支持量子电路的可视化
实现量子错误纠正
添加量子态的可视化表示