（纯新手教学）计算机视觉（opencv）实战十一——轮廓近似（cv2.approxPolyDP）

轮廓近似（`cv2.approxPolyDP`）详解

系统性地讲清楚 什么是轮廓近似、背后的算法逻辑、各参数的含义、epsilon 如何选、代码每行在做什么、常见坑与调参思路。

1）一眼看懂：轮廓近似在做什么？

轮廓近似（Polygonal Approximation） 的目标是：

用更少的顶点 ，在误差不超过阈值 epsilon 的前提下，逼近原始轮廓曲线。它能把"密密麻麻的轮廓点"简化成"折线/多边形的关键拐点"，从而：

更便于形状理解（比如三角形、矩形、五边形......）；
降低运算复杂度（点少了，后续判断更快）；
提升鲁棒性（小毛刺、小噪声被平滑掉）。

2）核心算法直觉：Ramer--Douglas--Peucker（RDP）

OpenCV 的 approxPolyDP 使用的是经典的 RDP 算法。它的思想可以用一句话描述：

用一根直线把轮廓的首尾连起来，找出"偏离这根直线最远的点 "；

如果这最远距离 ≤ epsilon ，则"这根直线"就足够代表中间所有点；

否则把轮廓在"最远点"处一分为二，递归对两段重复上述过程。

误差度量 ：点到线段的最短欧氏距离。
递归终止 ：所有子段内的"最远点距离"都 ≤ epsilon。
结果：保留下来的"拐点/端点"集合，就是近似后的多边形顶点序列。

直观理解：给曲线上下各画一条"±epsilon 的走廊"，如果曲线始终在走廊内，就用一条直线代替；一旦冲出，就在冲出的地方"加一个顶点"再细化。

3）`approxPolyDP` 的参数与返回值，逐一吃透

复制代码

approx = cv2.approxPolyDP(curve, epsilon, closed)

curve ：输入轮廓，一般来自 findContours 的某个元素，比如 contours[i]。
形状通常是 (N, 1, 2) 的 ndarray，含 N 个点，每点是 (x, y)。
epsilon ：近似精度（像素单位）。这是整个函数的"灵魂参数"。
- 它是"允许的最大几何偏差（最大欧氏距离）"。
- 越小：保留点越多、越贴近 原始轮廓；
  越大：点越少、越粗略，甚至把复杂形状"拉直"成几条线。
- 你在代码里将 epsilon 设为 "一定比例 × 周长"（见下节），这是非常实用的尺度自适应方式。
closed：布尔值，轮廓是否封闭。
- True：输入曲线被看作首尾相连的闭合轮廓；
- False：当作折线段处理。
  
  闭合与否会影响"首尾连线"的判断与误差度量，从而影响最终拐点。
返回值 approx ：近似后的轮廓，形状同样是 (M, 1, 2)，其中 M ≤ N。

也就是保留下来的"关键顶点坐标"。

4）为什么常用 `epsilon = α × arcLength(contour, True)`？

你在两段代码里分别用了：

epsilon = 0.01 * cv2.arcLength(contours[0], True)
epsilon = 0.005 * cv2.arcLength(contours[1], True)

这是非常实战的套路，因为：

epsilon 的单位是像素（绝对量）。同一张图里，物体大则需要更大的绝对误差、物体小则需要更小的绝对误差。
用周长 arcLength 的比例 来设置 epsilon，相当于做了尺度归一化 ：物体越大，epsilon 随之按比例变大；物体越小，epsilon 也按比例变小。
经验上：
- 0.5% ~ 1%：保形较好，细节完整，点数较多；
- 1% ~ 3%：常用区间，适合大多数"形状识别"的近似；
- >5%：强力简化（对噪声也很"宽容"），适合轮廓很规整、你只要粗略形状的任务。

5）与 `findContours`、`CHAIN_APPROX_*` 的关系

你的两段代码都用 cv2.findContours(..., cv2.RETR_TREE, cv2.CHAIN_APPROX_NONE) 拿到原始轮廓，其中：

RETR_TREE ：构建完整的层级结构（父子、同级关系）。适合有"洞/内外轮廓"的对象（比如花瓣内部的小空洞）。
CHAIN_APPROX_NONE ：保留轮廓上的每个点 。

这会让原始 contour 的点很多（例如 (N, 1, 2) 中 N 非常大），随后用 approxPolyDP 来做统一的几何简化 。

若选择 CHAIN_APPROX_SIMPLE，直线段上的中间点会先被压缩掉，N 会更小，再近似的空间也更有限。

小贴士：findContours 会修改输入图像 ，所以通常对阈值图的拷贝调用，或者像你这样直接对阈值图用也行，只是后面别再指望那张二值图还保持原样。

6）示例代码

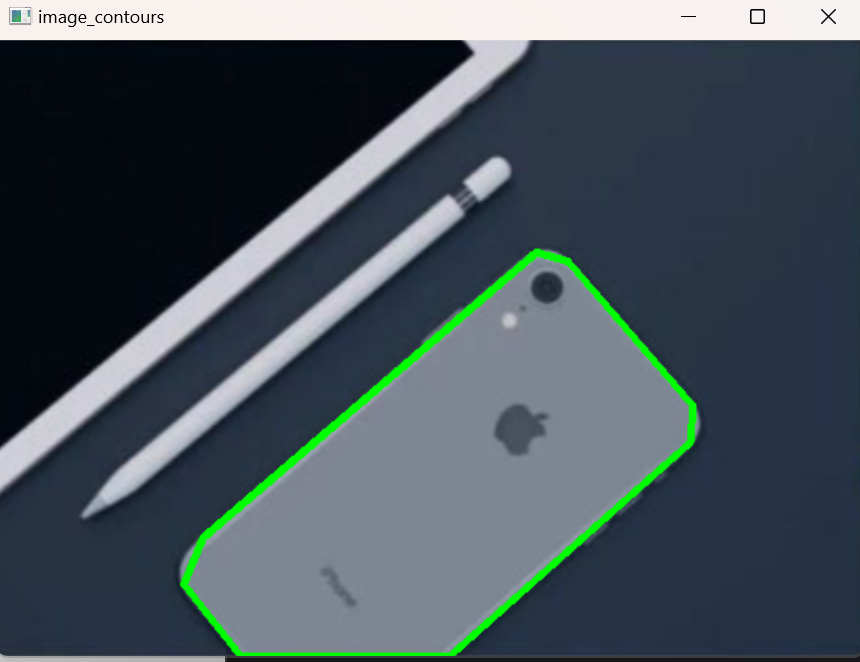
A. `phone.png` 示例

复制代码

import cv2
phone = cv2.imread('phone.png')
phone_gray = cv2.cvtColor(phone,cv2.COLOR_BGR2GRAY) # 转灰度
ret,phone_thresh = cv2.threshold(phone_gray, 120, 255, cv2.THRESH_BINARY)  # 二值化
contours = cv2.findContours(phone_thresh,cv2.RETR_TREE,cv2.CHAIN_APPROX_NONE)[-2]

通过固定阈值 120 将手机轮廓"抠"出来。
contours 是列表，每个元素是一个 (N, 1, 2) 的轮廓点集。

注意：contours[0] 并不保证是"最大轮廓" ，只是扫描顺序中的第一个。有时它可能是背景边缘、某个小部件等。这里直接取 [0]，在这张图里是手机的主外轮廓，但通用写法里通常会根据 cv2.contourArea 或层级信息来挑选。

epsilon = 0.01 * cv2.arcLength(contours[0], closed= True)
approx = cv2.approxPolyDP(contours[0], epsilon, closed= True)
print(contours[0].shape) # 形如 (N,1,2)
print(approx.shape) # 形如 (M,1,2)，M << N
这里 epsilon 取 1% 周长，属于"保形较好但有一定简化"的常用选择。
approx 的顶点数会明显少于 contours[0]，如果手机轮廓比较规整，最终顶点数可能接近矩形的 4 个（若椭圆/圆角较多，则略多于 4）。

phone_new = phone.copy()
image_contours = cv2.drawContours(phone_new, [approx],contourIdx=-1,color=(0,255,0),thickness=3)#绘制轮廓
cv2.imshow('phone',phone)
cv2.waitKey(0)
cv2.imshow('image_contours',image_contours)
cv2.waitKey(0)
drawContours 的第二个参数 要传"轮廓列表 "。你这里传 [*approx*]（列表套一个近似轮廓），这是规范写法。
contourIdx=-1 表示画列表中的全部轮廓（此处就一个）。
绿色粗线能直观看到"近似多边形"的样子。

运行时打印的 (N,1,2) 与 (M,1,2) 能直观看到"压点效果"。例如 N=2000，M=8 之类，这表示算法把 2000 个密集点浓缩成 8 个多边形顶点。

B. `hua.png` 示例

复制代码

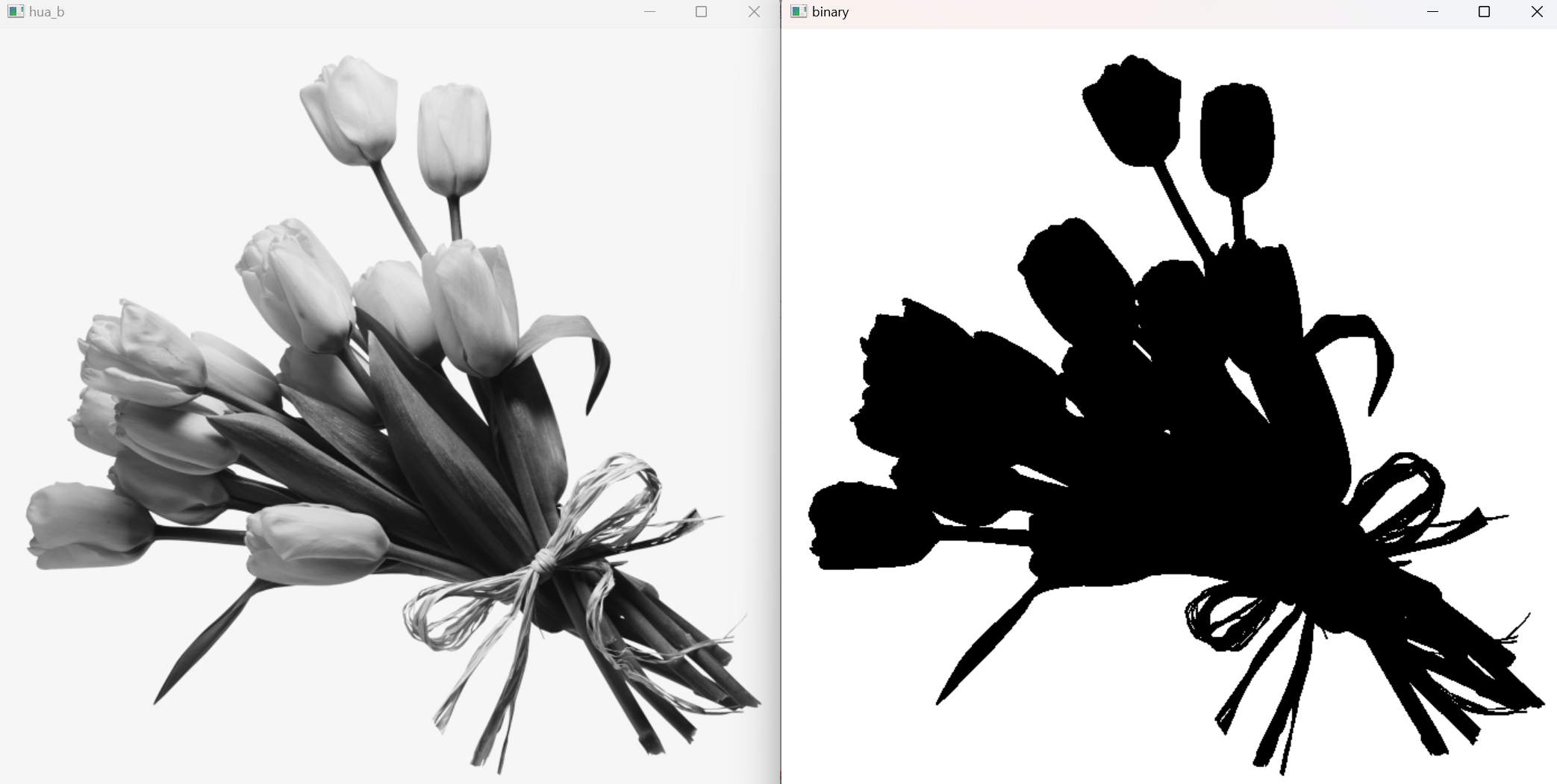
import cv2

hua = cv2.imread('hua.png')#读取原图
hua_gray = cv2.cvtColor(hua,cv2.COLOR_BGR2GRAY)#灰度图的处理
cv2.imshow('hua_b',hua_gray)
cv2.waitKey(0)
# hua_gray=cv2.imread('hua.png',0)  #读取灰度图
ret, hua_binary = cv2.threshold(hua_gray,240,255, cv2.THRESH_BINARY)#阈值处理为二值
cv2.imshow('binary',hua_binary)
cv2.waitKey(0)

# _,contours, hierarchy = cv2.findContours(hua_binary, cv2.RETR_TREE, cv2.CHAIN_APPROX_NONE)
contours = cv2.findContours(hua_binary, cv2.RETR_TREE, cv2.CHAIN_APPROX_NONE)[-2]  # 通用

阈值设为 240 很高，适合把**很亮的区域（花瓣/白色）**抠出来，但对光照不均的图像，可能会导致边界断裂或漏检。
使用 RETR_TREE 可以拿到"花朵外轮廓 + 内部洞/细节"的层次结构，后续如果需要筛选特定层（外轮廓 vs 内轮廓），要结合 hierarchy 使用。

复制代码

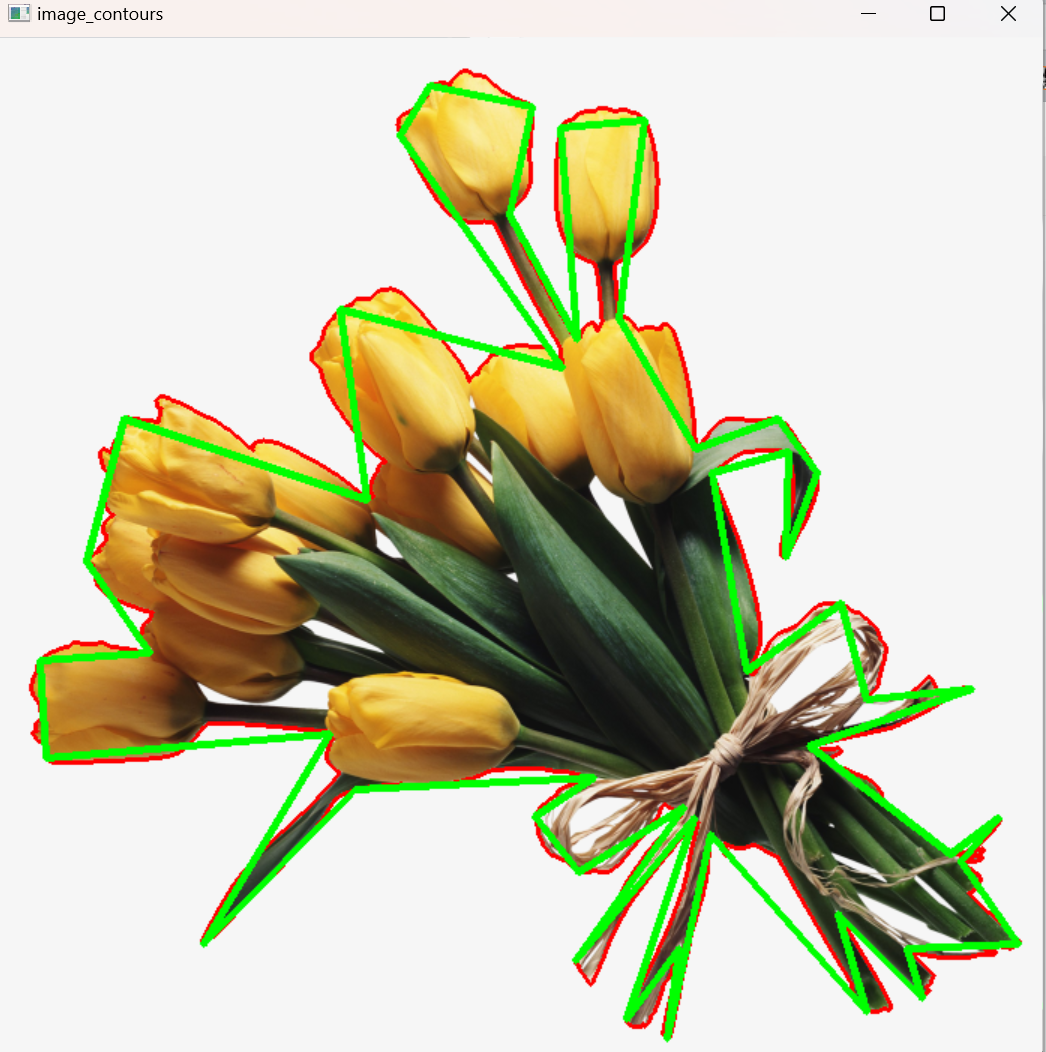
image_copy = hua.copy()
cv2.drawContours(image=image_copy, contours=contours[1], contourIdx=-1,color=(0,0,255),thickness=2)
cv2.imshow('Contours_show', image_copy)
cv2.waitKey(0)

这里给出一个兼容性提醒 ：drawContours 的 contours 期望一个"列表" ，如 contours=[contours[1]]；

你传的是单个 ndarray（contours[1]），在一些 OpenCV 版本中也许能画 ，但在另一些版本里可能报错或行为不一致。

你的下一次调用已使用 [approx] 这种稳妥写法；如果你发现这一行在某些环境报错，可将它也包成列表（这里我不改你的代码，只说明风险点）。

epsilon = 0.005 * cv2.arcLength(contours[1], closed= True) #设置近似精度【h要<ε；ε越小，点越多，越精确】
approx = cv2.approxPolyDP(contours[1], epsilon, closed= True) #对轮廓进行近似
print("原始轮廓点数：", contours[1].shape)
print("近似轮廓点数：", approx.shape)
hua_new = hua.copy()
image_contours = cv2.drawContours(image_copy, [approx],contourIdx=-1,color=(0,255,0),thickness=3)#绘制轮廓
cv2.imshow('image_contours',image_contours)
cv2.waitKey(0)
这里 epsilon 取 0.5% 周长 ，比手机示例更"紧"，因为花瓣边缘往往更细腻复杂，想尽量保留更多形状细节。
画出来的绿色轮廓应该比红色原轮廓更"干净"，点更少，但保持花瓣的大致形状。

7）`epsilon` 的调参方法与经验区间

先相对、后微调 ：先取 epsilon = α × arcLength(contour)，再在 α ∈ [0.003, 0.02] 的区间内试探。
- 目标是"尽量少的点 + 形状不走样"。
看任务：
- 形状识别/顶点计数（如判定三角形/矩形） ：α 可取 1%~3%，让噪声被吸收，保持边角清晰。
- 需要保留细腻轮廓细节（自然物体、曲线） ：α 取 0.3%~1%。
- 粗略外接形体、只要大轮廓趋势 ：α 取 >3% ，甚至 5%~10%。
尺度影响 ：epsilon 是像素单位，图像缩放会直接影响"绝对误差"。用周长归一能抵消这点，但极端缩放 时仍建议重新评估 α。

8）与相近概念/算子区别（别混淆）

approxPolyDP ：用多边形顶点近似原轮廓，保形为主，允许曲线被"折线化"。
凸包 cv2.convexHull ：得到最小凸多边形 包住轮廓，会抹掉凹陷（比如星形被"鼓起来"）。
最小外接矩形 cv2.minAreaRect ：找一个面积最小的旋转矩形包住目标；只有 4 个角，信息压缩极强。
外接圆/椭圆：拟合一个圆/椭圆；更强的形状假设，形状表达单一。
CHAIN_APPROX_SIMPLE （在 findContours 阶段）与 approxPolyDP（事后多边形近似）不可等价：前者只是把直线段上的冗余点 去掉，后者是几何近似，会综合考虑曲率变化。

9）质量与稳健性：前处理 & 版本差异 & 轮廓顺序

前处理 影响巨大：二值化阈值过高/过低都会破坏轮廓；

适当的 去噪（如中值滤波）、形态学闭运算 能让轮廓更连贯，从而近似更稳定。
OpenCV 版本差异 ：findContours 在不同版本里返回 (image, contours, hierarchy) 或 (contours, hierarchy)；

你用的 [-2] 取法能兼容不同版本（稳妥）。
contours 的顺序不等于大小顺序 ：不要理所当然地把 contours[0] 当最大轮廓。需要时应结合 cv2.contourArea 或 hierarchy 进行筛选（比如只取外层、忽略洞等）。

10）常见"坑位"清单

epsilon 太小

点几乎不减，近似意义不大；时间也照样花，甚至更久。
epsilon 太大

关键拐点被吃掉，矩形被"拉直"成三角形，形状判别失败。
closed 标志不当

封闭轮廓却用 False，或开放轮廓却用 True，会影响"首尾连线"的误差统计，导致顶点异常。
传错 drawContours 的参数类型

第二个参数应为列表（如 [approx]），不同版本的 OpenCV 对"直接传单个 ndarray"的容忍度不同。
误把轮廓顺序当语义顺序
contours[i] 的索引只是扫描顺序，跟"外层/内层""大小""位置"没有必然关系。
二值化/边缘裂缝

轮廓断裂会让近似结果"漏点、缺角"。可在阈值前先平滑，或阈值后做形态学闭运算。

11）怎么用近似结果做"形状识别"？

数顶点 ：len(approx) 即多边形的顶点数。
- 3≈三角形，4≈四边形，5≈五边形......
- 对四边形再看角度是否接近 90° 来区分矩形/菱形。
面积一致性 ：比较 cv2.contourArea(approx) 与 cv2.contourArea(contour) 的比值（应当接近 1）。
周长一致性 ：比较 arcLength 的比值；若差距过大，说明简化过头或轮廓不规整。

这些后处理都直接基于你当前代码的输出 （approx），无需改动你的流程。

12）原始轮廓和近似轮廓、`epsilon`

print(shape)：
- 原始轮廓：形如 (N,1,2)，N 很大；
- 近似轮廓：形如 (M,1,2)，M 明显变小（矩形场景下接近 4）。
可视化窗口：
- phone：绿色粗线会勾出简化后的"手机外形多边形"；
- hua：绿色粗线会显示简化后的花瓣轮廓；红色（若成功绘制）是原轮廓对照。
epsilon 不同带来的对比：
- 0.01×周长（手机） vs 0.005×周长（花）：后者更"贴边"、保留细节更多。

总结一句话 ：
approxPolyDP 用 epsilon 这把"精度刻刀"，在"保留形状特征"和"减少点数噪声"之间做权衡。你当前两段代码是非常标准的用法：先阈值出轮廓 → 用 RETR_TREE 和 CHAIN_APPROX_NONE 获得完整点集 → 用 epsilon = 周长比例 做尺度自适应近似 → 可视化比较原始与近似的点数与形状。后续无论是做形状分类、关键点提取，还是外接几何体拟合，都能在这个"简化后的轮廓"上更稳定地进行。

（纯新手教学）计算机视觉（opencv）实战十一——轮廓近似（cv2.approxPolyDP）

轮廓近似（cv2.approxPolyDP）详解

1）一眼看懂：轮廓近似在做什么？

2）核心算法直觉：Ramer--Douglas--Peucker（RDP）

3）approxPolyDP 的参数与返回值，逐一吃透

4）为什么常用 epsilon = α × arcLength(contour, True)？

5）与 findContours、CHAIN_APPROX_* 的关系

6）示例代码

A. phone.png 示例

B. hua.png 示例

7）epsilon 的调参方法与经验区间

8）与相近概念/算子区别（别混淆）

9）质量与稳健性：前处理 & 版本差异 & 轮廓顺序

10）常见"坑位"清单

11）怎么用近似结果做"形状识别"？

12）原始轮廓和近似轮廓、epsilon

轮廓近似（`cv2.approxPolyDP`）详解

3）`approxPolyDP` 的参数与返回值，逐一吃透

4）为什么常用 `epsilon = α × arcLength(contour, True)`？

5）与 `findContours`、`CHAIN_APPROX_*` 的关系

A. `phone.png` 示例

B. `hua.png` 示例

7）`epsilon` 的调参方法与经验区间

12）原始轮廓和近似轮廓、`epsilon`