PyTorch 损失函数与优化器全面指南：从理论到实践

vvilkim2025-09-04 10:44

在深度学习的世界里，损失函数和优化器是模型训练的两大核心组件。它们如同导航系统中的指南针和引擎，共同决定了模型学习的正确方向和效率。PyTorch作为当前最流行的深度学习框架之一，提供了丰富而灵活的损失函数和优化器实现。本文将深入探讨PyTorch中的交叉熵损失(CrossEntropy)、均方误差损失(MSE)以及随机梯度下降(SGD)和Adam优化器，帮助读者全面理解它们的原理、实现和应用场景。

第一部分：损失函数------模型性能的衡量标准

1.1 损失函数的作用与意义

损失函数（Loss Function），也称为代价函数（Cost Function），是衡量模型预测输出与真实值差异的数学表达式。在深度学习中，损失函数扮演着至关重要的角色：

  1. 性能评估：量化模型预测的准确程度

  2. 训练导向：为优化器提供梯度信息，指导参数更新方向

  3. 问题适配：不同任务需要不同的损失函数（分类vs回归）

一个好的损失函数应该能够准确反映模型在当前任务上的表现，同时具有良好的数学性质（如可微性），便于优化。

1.2 交叉熵损失(CrossEntropyLoss)

理论背景

交叉熵源于信息论，用于衡量两个概率分布之间的差异。在分类问题中，我们希望模型的预测概率分布尽可能接近真实的标签分布。

数学表达式为：

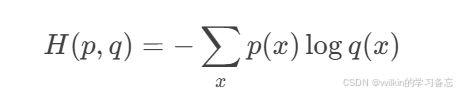
其中p是真实分布，q是预测分布。

PyTorch实现详解
复制代码 
import torch
import torch.nn as nn

# 初始化
criterion = nn.CrossEntropyLoss()

# 输入输出说明
# inputs - (N,C) 其中N是batch大小，C是类别数（未经过softmax的原始分数）
# target - (N) 每个元素是类别索引(0 ≤ target[i] ≤ C-1)

# 示例
outputs = torch.randn(3, 5)  # 3个样本，5个类别
labels = torch.tensor([1, 0, 4])  # 真实类别索引

loss = criterion(outputs, labels)
关键特性

  1. 内部机制：实际上结合了LogSoftmax和NLLLoss两个操作

  2. 数值稳定性：内部实现避免了单独计算softmax可能导致的数值不稳定问题

  3. 类别加权：支持通过weight参数处理类别不平衡问题

    复制代码 
    # 类别加权示例
weights = torch.tensor([0.1, 0.9, 0.3, 0.7, 0.5])  # 为每个类别设置权重
criterion = nn.CrossEntropyLoss(weight=weights)

  4. 忽略特定类别：可通过ignore_index参数忽略某些类别的计算

适用场景

  • 多类别分类问题

  • 输出是互斥的类别标签

  • 如图像分类、文本分类等

1.3 均方误差损失(MSELoss)

理论背景

均方误差（Mean Squared Error）是最常用的回归损失函数，计算预测值与真实值之间差值的平方的平均。

数学表达式：

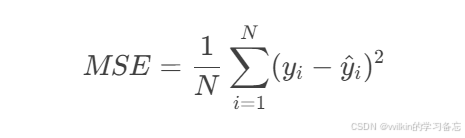
PyTorch实现详解
复制代码 
mse_loss = nn.MSELoss()

# 输入维度可以是任意形状，只要prediction和target形状相同
predictions = torch.tensor([1.0, 2.0, 3.0], requires_grad=True)
targets = torch.tensor([1.5, 2.5, 2.9])

loss = mse_loss(predictions, targets)
变体形式

PyTorch还提供了MSELoss的几种变体：

复制代码 
# 求和而非平均
mse_sum = nn.MSELoss(reduction='sum')

# 不计算平均或求和，输出元素级损失
mse_none = nn.MSELoss(reduction='none')
关键特性

  1. 对异常值敏感：由于平方操作，大误差会被显著放大

  2. 可微性：处处可微，利于梯度下降优化

  3. 尺度敏感：受数据尺度影响大，通常需要特征缩放

适用场景

  • 回归问题（房价预测、温度预测等）

  • 输出是连续值的问题

  • 当大误差需要被重点惩罚的场景

第二部分：优化器------模型训练的动力引擎

2.1 优化器的作用与原理

优化器（Optimizer）负责根据损失函数的梯度更新模型参数，其核心目标是通过最小化损失函数来提升模型性能。优化算法的选择直接影响：

  1. 模型收敛速度

  2. 最终模型性能

  3. 训练过程的稳定性

2.2 随机梯度下降(SGD)

理论基础

SGD是最基础的优化算法，其参数更新公式为：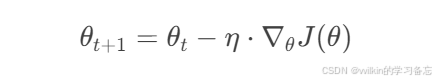

其中η是学习率。

PyTorch实现详解
复制代码 
import torch.optim as optim

# 基本SGD
optimizer = optim.SGD(model.parameters(), lr=0.01)

# 带momentum的SGD
optimizer_momentum = optim.SGD(model.parameters(), lr=0.01, momentum=0.9)

# 带L2正则化的SGD
optimizer_weightdecay = optim.SGD(model.parameters(), lr=0.01, weight_decay=1e-4)
关键参数解析

  1. 学习率(lr)：最重要的超参数，控制参数更新步长

  2. 动量(momentum)：帮助加速相关方向的学习，抑制振荡

    • 经验值：0.9左右

  3. 权重衰减(weight_decay)：L2正则化系数，防止过拟合

  4. 阻尼(dampening)：动量阻尼，通常不需要修改

训练循环模板
复制代码 
for epoch in range(epochs):
    for data, target in dataloader:
        optimizer.zero_grad()  # 清除旧梯度
        output = model(data)   # 前向传播
        loss = criterion(output, target)  # 计算损失
        loss.backward()        # 反向传播
        optimizer.step()       # 参数更新
优缺点分析

优点：

  • 简单易懂

  • 对小数据集和简单模型效果良好

  • 更容易收敛到全局最优（相比自适应方法）

缺点：

  • 需要精心调参（特别是学习率）

  • 在复杂地形（损失曲面）中可能收敛缓慢

  • 对所有参数使用相同学习率

2.3 Adam优化器

理论基础

Adam（Adaptive Moment Estimation）结合了动量法和RMSProp的优点，通过计算梯度的一阶矩估计和二阶矩估计来调整每个参数的学习率。

更新规则：

  1. 计算梯度的一阶矩（均值）和二阶矩（未中心化的方差）

  2. 进行偏差校正

  3. 更新参数

PyTorch实现详解
复制代码 
optimizer = optim.Adam(model.parameters(), 
                      lr=0.001,
                      betas=(0.9, 0.999),
                      eps=1e-08,
                      weight_decay=0)
关键参数解析

  1. 学习率(lr)：通常设为0.001

  2. betas：动量相关参数

    • beta1：一阶矩估计的衰减率（通常0.9）

    • beta2：二阶矩估计的衰减率（通常0.999）

  3. eps：数值稳定性常数（通常不需修改）

  4. weight_decay：L2正则化系数

进阶变体
复制代码 
# AdamW - 更正确的权重衰减实现
optimizer_adamw = optim.AdamW(model.parameters(), lr=0.001)

# Amsgrad - Adam的变体，解决收敛问题
optimizer_amsgrad = optim.Adam(model.parameters(), amsgrad=True)
优缺点分析

优点：

  • 自适应学习率，减少调参需求

  • 适合大规模数据和参数

  • 通常收敛更快

  • 适合非平稳目标和稀疏梯度问题

缺点：

  • 可能收敛到次优解

  • 内存占用略高（需要保存动量）

  • 某些情况下泛化性能不如SGD

第三部分：实践应用与选择指南

3.1 损失函数选择策略

  1. 分类问题：

    • 多类别单标签：CrossEntropyLoss

    • 多类别多标签：BCEWithLogitsLoss

    • 类别不平衡：Focal Loss

  2. 回归问题：

    • 一般情况：MSELoss

    • 异常值较多：L1Loss（更鲁棒）

    • 需要平衡L1/L2：SmoothL1Loss

  3. 特殊任务：

    • 目标检测：各种IoU Loss

    • 生成对抗网络：对抗损失

    • 序列建模：CTCLoss

3.2 优化器选择策略

优化器 适用场景 学习率建议 备注
SGD 小数据集、简单模型、需要精细调优 0.01-0.1 加momentum(0.9)效果更好
Adam 大多数深度学习任务 0.001左右 默认选择
AdamW 使用权重衰减时 同Adam 特别是Transformer类模型
RMSprop RNN/LSTM网络 0.001 对循环网络效果好

3.3 学习率调整技巧

  1. 学习率预热：初期使用较小学习率，逐步增大

    复制代码 
    scheduler = optim.lr_scheduler.LinearLR(optimizer, start_factor=0.1, total_iters=5)

  2. 周期性调整：

    复制代码 
    scheduler = optim.lr_scheduler.StepLR(optimizer, step_size=30, gamma=0.1)

  3. 基于验证集表现调整：

    复制代码 
    scheduler = optim.lr_scheduler.ReduceLROnPlateau(optimizer, 'min', patience=5)

3.4 调试技巧

  1. 损失不下降：

    • 检查学习率是否合适

    • 确认梯度是否正常传播（打印梯度值）

    • 检查数据预处理是否正确

  2. 训练不稳定：

    • 尝试减小学习率

    • 增加batch size

    • 使用梯度裁剪（clip_grad_norm_）

  3. 过拟合：

    • 增加权重衰减

    • 尝试SGD优化器

    • 添加正则化项

第四部分：综合实例分析

4.1 图像分类完整示例

复制代码 
import torch
import torch.nn as nn
import torch.optim as optim
from torchvision import datasets, transforms

# 数据准备
transform = transforms.Compose([
    transforms.ToTensor(),
    transforms.Normalize((0.5,), (0.5,))
])
train_set = datasets.MNIST('./data', download=True, train=True, transform=transform)
train_loader = torch.utils.data.DataLoader(train_set, batch_size=64, shuffle=True)

# 简单模型
model = nn.Sequential(
    nn.Flatten(),
    nn.Linear(28*28, 128),
    nn.ReLU(),
    nn.Linear(128, 10)
)

# 损失函数和优化器
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)

# 训练循环
for epoch in range(10):
    for images, labels in train_loader:
        optimizer.zero_grad()
        outputs = model(images)
        loss = criterion(outputs, labels)
        loss.backward()
        optimizer.step()
    print(f'Epoch {epoch+1}, Loss: {loss.item():.4f}')

4.2 回归问题完整示例

复制代码 
# 回归问题示例 - 波士顿房价预测
from sklearn.datasets import load_boston
from sklearn.preprocessing import StandardScaler

# 数据准备
boston = load_boston()
X = StandardScaler().fit_transform(boston.data)
y = boston.target

# 转换为tensor
X_tensor = torch.FloatTensor(X)
y_tensor = torch.FloatTensor(y).view(-1, 1)

# 简单回归模型
model = nn.Sequential(
    nn.Linear(13, 64),
    nn.ReLU(),
    nn.Linear(64, 1)
)

# MSE损失和SGD优化器
criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.9)

# 训练循环
for epoch in range(100):
    optimizer.zero_grad()
    predictions = model(X_tensor)
    loss = criterion(predictions, y_tensor)
    loss.backward()
    optimizer.step()
    if epoch % 10 == 0:
        print(f'Epoch {epoch}, Loss: {loss.item():.4f}')

结语

损失函数和优化器是深度学习模型训练的核心组件，理解它们的工作原理和适用场景对于构建高效模型至关重要。PyTorch提供了丰富的实现，从经典的SGD到自适应的Adam，从CrossEntropy到各种回归损失。在实践中，需要根据具体问题和数据特点选择合适的组合，并通过实验找到最佳超参数设置。记住，没有放之四海而皆准的最佳选择，只有最适合特定任务的解决方案。希望本文能帮助你在PyTorch的世界里更加得心应手地训练出高性能的深度学习模型。

相关推荐
fsnine3 小时前
深度学习——卷积神经网络
人工智能·深度学习·cnn
三之又三4 小时前
卷积神经网络CNN-part2-简单的CNN
人工智能·神经网络·cnn
Niuguangshuo4 小时前
Python绘图动态可视化：实时音频流
开发语言·python·音视频
机器之心4 小时前
谷歌放出Nano Banana六大正宗Prompt玩法，手残党速来
人工智能·openai
0wioiw04 小时前
Python基础（⑦魔法方法）
开发语言·python
艾醒4 小时前
大模型面试题剖析：大模型微调数据集构建
人工智能·算法·程序员
白应穷奇4 小时前
编写高性能数据处理代码 - Pipeline-Style
后端·python·性能优化
慧都小项4 小时前
构建安全的自动驾驶：软件测试中的编码规范与AI验证
人工智能·测试工具·安全·自动驾驶·parasoft
GEO_JYB4 小时前
车载卫星通信：让自动驾驶“永不掉线”？
人工智能
热门推荐
01UV安装并设置国内源02奈飞工厂官网，国内Netflix影视在线看|中文网页电脑版入口03Xget：下一代开源资源获取加速引擎，让你的文件下载、储存库克隆和镜像拉取快如闪电04Qwen3-Coder 快速上手教程 | Qwen Code + Claude Code05Linux下V2Ray安装配置指南06不再让Windows更新！&Edge游戏助手卸载及关闭自动更新07KGG转MP3工具|非KGM文件|解密音频08A股预测还能更准？开源大模型Kronos带你跑通预测+回测全流程09jdk21下载、安装（Windows、Linux、macOS）10使用国内镜像网站在线下载安装Qt（解决官网慢的问题）——Qt