本算法复现了 RoboDK 的机器人校准功能:在校准集的精度表现与 RoboDK 一致 ,在验证集的精度表现接近 Staubli 原厂。
参考:RoboDK 机器人校准功能(https://robodk.com.cn/cn/robot-calibration)
一分钟读懂解决了啥

机械臂出厂有一套"尺寸与装配"参数(DH 表),但现实里总会有微小偏差 。结果就是:机械臂"以为"自己到了某点,真实位置 却差了几到几十毫米。校准 的目的,就是用高精度测量数据反推出DH参数的这些偏差,再写回控制器,让机器人之后走位更准。
本工程做了三件事:
- 自动估计 :根据你现场测量的机械臂末端位置,联合估计DH 参数 + 机械臂基座6D位姿 + 工具中心点3D位置 (以下将这三组参数统称为机械臂几何参数);
- 效果可见 :自动生成机械臂的校准报告 与校准前后误差对比直方图;
- 实机验证 :在 Staubli TX2-90L 、TX200 型号机械臂上测试,校准效果与 RoboDK 基本一致,写回控制器后的实测精度接近 Staubli 原厂。
关键概念
校准集(Calibration set)
用于"学习"的样本:给出一组关节空间点位,机械臂运动到对应关节位置后,记录末端执行器的实测 3D 位置。算法据此估计/标定 更准确的 机械臂几何参数。(可理解为"课内练习")
验证集(Validation set)
将标定得到的几何参数写入到机械臂控制器并启用 后,选取不同于校准集的新点位,再次采集末端 3D 位置以评估实际表现。(可理解为"期末考试")
为何验证集的误差通常略高于校准集的误差
在有限样本下,估计的几何参数对校准集更"贴合",而在未参与优化的数据上误差略高是常见现象。按照通用工程经验:只要验证集的误差 ≪ 原始误差 ,且与校准集的误差 的差距不大(同数量级、趋势一致),即可认为该组几何参数具有良好的泛化能力 与工程可用性。
误差统计说明
- 本文所有位置误差 单位均为 mm(毫米)。
- 报告中的 90%max 可视为误差的 90 百分位(P90) :即 90% 的样本误差低于该值。
- σ/6σ :σ 为标准差,6σ 为 6 倍标准差,均基于样本误差统计,用于快速判断误差分布的离散程度 与波动范围。
给定关节角 J \mathbf{J} J 的前向运动学公式
-
校准前(缺省 SDH)
T tcp world = T base world ⋅ T flange base ( J ) (默认 SDH) ⋅ T tcp flange \;\mathbf T_{\text{tcp}}^{\text{world}}\;=\;\mathbf T_{\text{base}}^{\text{world}}\;\cdot\;\underset{\text{(默认 SDH)}}{\mathbf T_{\text{flange}}^{\text{base}}(\mathbf J)}\;\cdot\;\mathbf T_{\text{tcp}}^{\text{flange}}\; Ttcpworld=Tbaseworld⋅(默认 SDH)Tflangebase(J)⋅Ttcpflange
-
校准后(优化 SDH)
T tcp world ′ = T base world ′ ⋅ T flange base ′ ( J ) (优化 SDH) ⋅ T tcp flange ′ \;{\mathbf T_{\text{tcp}}^{\text{world}}}'\;=\;{\mathbf T_{\text{base}}^{\text{world}}}'\;\cdot\;\underset{\text{(优化 SDH)}}{{\mathbf T_{\text{flange}}^{\text{base}}}'(\mathbf J)}\;\cdot\;{\mathbf T_{\text{tcp}}^{\text{flange}}}'\; Ttcpworld′=Tbaseworld′⋅(优化 SDH)Tflangebase′(J)⋅Ttcpflange′
简明结论
TX2-90L:
- 原始的平均误差 ≈ 0.47 mm ,90%max ≈ 0.65 mm;
- 校准集的平均误差 ≈ 0.04 mm ,90%max ≈ 0.06 mm;
- 验证集的平均误差 ≈ 0.05 mm ,90%max ≈ 0.08 mm;
TX200:
- 原始的平均误差 ≈ 1.285 mm ,90%max ≈ 1.673 mm;
- 校准集的平均误差 ≈ 0.142 mm ,90%max ≈ 0.214 mm;
- 验证集的平均误差 ≈ 0.144 mm ,90%max ≈ 0.246 mm;
一句话总结 :在 TX2-90L 与 TX200 上,本算法成功复现 RoboDK 的校准能力;写回控制器后的实测绝对精度接近 Staubli 原厂。
项目亮点
- 想校哪就校哪 :每个关节的 α / a / θ / d 都能单独选择是否参与校准(省时也降低"过拟合"风险)。
- 一步到位 :不止校正DH 参数 ,还把机械臂基座6D位姿 ,工具中心点3D位置一起估出来。
- 有图有报告 :自动导出校准报告 与前后误差对比直方图,量化效果一目了然。
- 带真实样例 :内置 TX2-90L / TX200的现场真实测量数据(校准集与验证集),即刻复现文中结果。
- 可视化脚本:遇到异常样本与法向问题,辅助脚本能快速定位。
校准效果
实验对象:TX2-90L 机械臂
机械臂简介与原厂精度

数据来源:robodk.com/robot/Staubli/TX2-90L
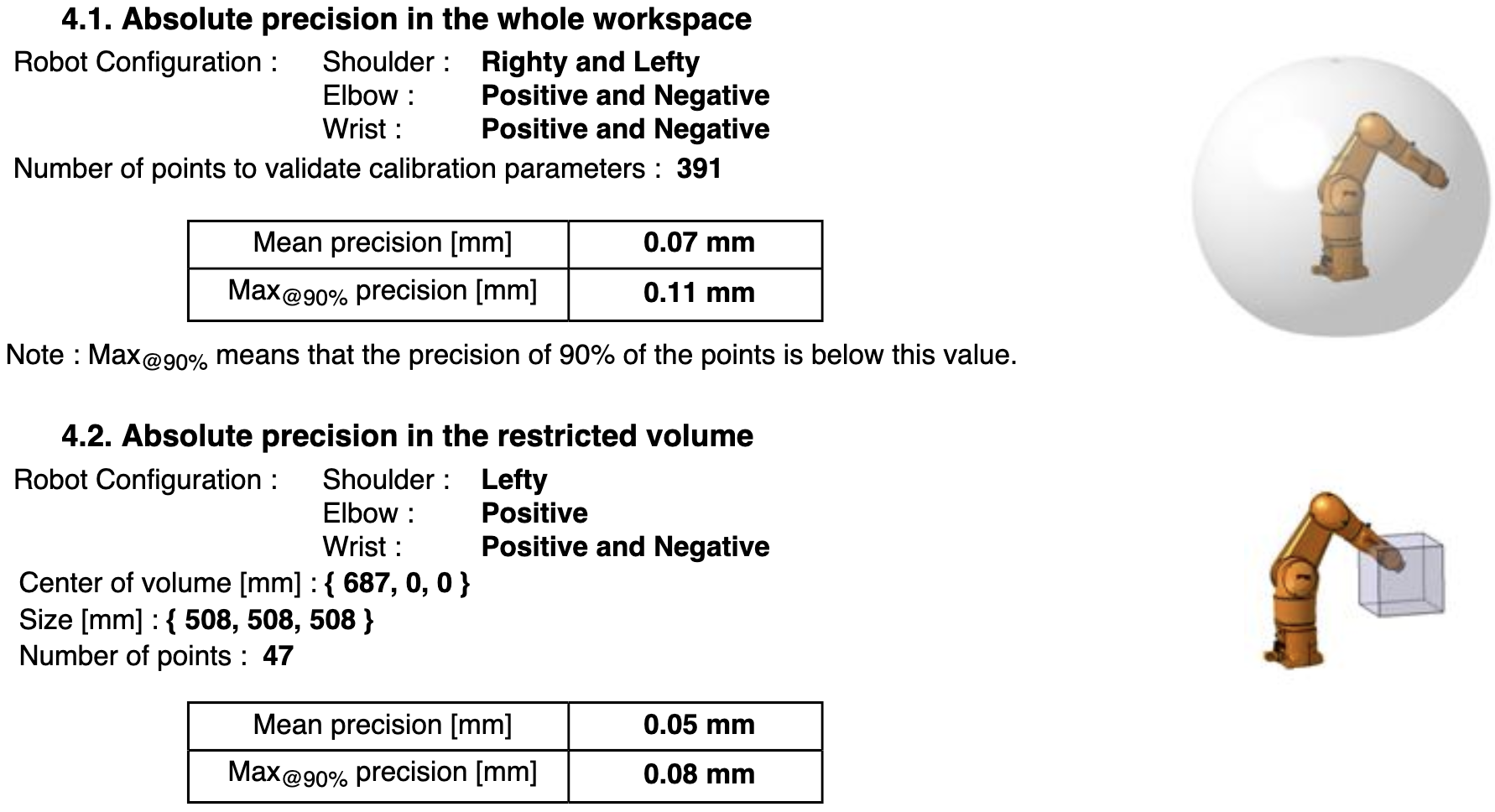
Staubli 原厂绝对定位精度:全工作空间 mean 0.07 mm、90%max 0.11 mm;在 508×508×508 mm 立方体子域内 mean 0.05 mm、90%max 0.08 mm。
数据来源: 代码的工作路径/doc/TX2-90L/AbsoluteCalibrationQualityReport_TX2-90L.pdf
校准对比与结论
绝对定位精度图示(单位:mm)
 本算法(校准集)校准前、后精度对比直方图
本算法(校准集)校准前、后精度对比直方图  RoboDK(校准集)校准前、后精度对比直方图
RoboDK(校准集)校准前、后精度对比直方图
绝对定位精度数据(单位:mm)
相同颜色为对比项。
| 算法 | 数据集 | 校准状态 | mean | max | 90%max | σ | 6σ | num of points |
|---|---|---|---|---|---|---|---|---|
| 本算法 | 校准集 | 校准前(原始) | 0.466283 | 0.874976 | 0.647841 | 0.152851 | 0.917108 | 60 |
| 本算法 | 校准集 | 校准后 | 0.039163 | 0.098429 | 0.062382 | 0.017692 | 0.106153 | 60 |
| 本算法 | 验证集 | 校准后 | 0.0509466 | 0.1020001 | 0.0838984 | --- | --- | 40 |
| RoboDK | 校准集 | 校准前(原始) | 0.466 | 0.875 | --- | 0.154 | 0.929 | 60 |
| RoboDK | 校准集 | 校准后 | 0.039 | 0.098 | --- | 0.018 | 0.093 | 60 |
| RoboDK | 验证集 | 校准后 | 0.051 | 0.102 | 0.084 | --- | --- | 40 |
原始数据与报表见
代码的工作路径/RobotCalib/doc/TX2-90L/与代码的工作路径/RobotCalib/results/TX2-90L/。
要点:
- 本算法与 RoboDK 在同一校准集上的结果一致量级。
- 验证集的精度位于 Staubli 原厂报告立方体子域水平附近。
- 验证集位姿分布与校准集不同,误差略有上浮,符合预期。
实验对象:TX200 机械臂
机械臂简介与原厂精度

数据来源:robodk.com/robot/Staubli/TX200
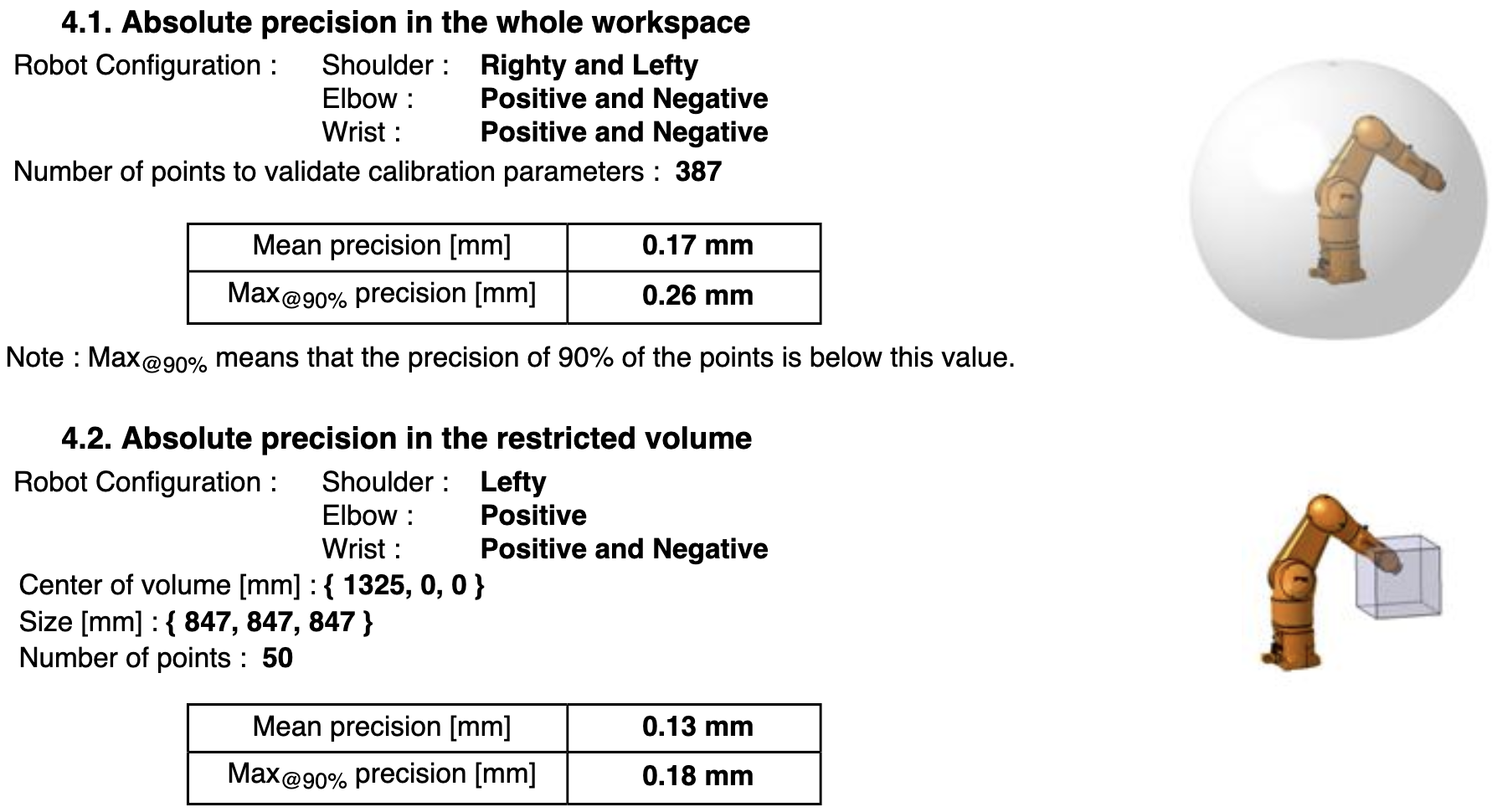
Staubli 原厂绝对定位精度:全工作空间 mean 0.17 mm、90%max 0.26 mm;在 847×847×847 mm 立方体子域内 mean 0.13 mm、90%max 0.18 mm。
数据来源: 代码的工作路径/doc/TX200/AbsoluteCalibrationQualityReport_TX200.pdf
校准对比与结论
绝对定位精度图示(单位:mm)
 本算法(校准集)校准前、后精度对比直方图
本算法(校准集)校准前、后精度对比直方图  RoboDK(校准集)校准前、后精度对比直方图
RoboDK(校准集)校准前、后精度对比直方图
绝对定位精度数据(单位:mm)
相同颜色为对比项。
| 算法 | 数据集 | 校准状态 | mean | max | 90%max | σ | 6σ | num of points |
|---|---|---|---|---|---|---|---|---|
| 本算法 | 校准集 | 校准前(原始) | 1.285361 | 2.141703 | 1.673369 | 0.306290 | 1.837739 | 107 |
| 本算法 | 校准集 | 校准后 | 0.142412 | 0.487590 | 0.213881 | 0.071394 | 0.428367 | 107 |
| 本算法 | 验证集 | 校准后 | 0.143818 | 0.501294 | 0.246057 | --- | --- | 44 |
| RoboDK | 校准集 | 校准前(原始) | 1.269 | 2.128 | --- | 0.309 | 2.196 | 107 |
| RoboDK | 校准集 | 校准后 | 0.142 | 0.488 | --- | 0.072 | 0.358 | 107 |
| RoboDK | 验证集 | 校准后 | 0.144 | 0.501 | 0.246 | --- | --- | 44 |
原始数据与报表见
代码的工作路径/RobotCalib/doc/TX200/与代码的工作路径/RobotCalib/results/TX200/。
要点:
- 本算法与 RoboDK 在同一校准集上的结果一致量级。
- 验证集的精度位于原厂全域与立方体子域之间;由于校准/验证子域范围较原厂报告的立方体子域更大,误差略有放大属预期。
- 验证集位姿分布更复杂,精度略低于校准集理论值。
总体结论
在 TX2-90L 与 TX200 两个样例上,本算法成功复现了 RoboDK 的校准能力;写入控制器后的实测绝对精度接近 Staubli 原厂校准水平。
环境依赖
- C++17 编译器(GCC 9+/Clang 10+/MSVC 2019+)
- CMake 3.16+
- Eigen 3
- Ceres Solver(含
EigenQuaternionParameterization) - yaml-cpp
- Python 3(可视化脚本:
numpy、matplotlib)
Ubuntu 示例:
bash
sudo apt update
sudo apt install -y build-essential cmake libeigen3-dev libyaml-cpp-dev libceres-dev \
python3 python3-pip
pip3 install -U numpy matplotlibmacOS (Homebrew):
bash
brew install cmake eigen ceres-solver yaml-cpp
pip3 install -U numpy matplotlib编译
终端进入工程目录
bash
mkdir build && cd build
cmake .. && make -j8可执行文件输出:build/RobotCalibration
快速开始(内置样例)
项目提供两套样例数据 TX2-90L / TX200,样例数据是我在现场使用高精度设备采集的,并提供两套校准模型选项 simple / complete,推荐使用complete校准模型,本文所有的校准数据均使用complete模型获得:
bash
# 运行样例:TX2-90L + complete
./build/RobotCalibration TX2-90L complete
# 运行样例:TX200 + complete
./build/RobotCalibration TX200 complete命令行参数:
Usage: RobotCalibration <robot_name: TX2-90L|TX200> <calib_mode: simple|complete>程序会自动读取:
- DH:
config/DH/<robot_name>-default.yml - 选项:
config/option/CalibConfig<Simple|Complete>.yml - 测量:
config/measured/<robot_name>/机器人校准-Calibration.csv(及 Base/Tool 初始化所需 CSV)
输出默认写入:results/<robot_name>/
输出与可视化
运行结束后,results/<robot_name>/ 下包含:
-
OptimalReport_<robot_name>.txt:- Base/Tool 外参(平移 + 四元数)
- 原始与优化后的 DH 表
- 逐样本三维位置误差及统计
-
accuracy_stats_hist_<robot_name>.png:校准前后的精度对比直方图
示例,OptimalReport_TX2-90L.txt如下:
powershell
========================== Calibration Report ==========================
[1]base2world Transformation( [X,Y,Z]mm|Quaternion[q1-q4] ):
331.331991, 349.413195, 429.000644, -0.000022, 0.002251, 0.001411, 0.999996
[2]tool2flange Transformation( [X,Y,Z]mm|Quaternion[q1-q4] ):
24.990101, 0.213438, 14.899634, 0.000000, 0.000000, 0.000000, 1.000000
[3] Original SDH Parameters:
Joint Alpha(deg) a(mm) theta(deg) d(mm)
------------------------------------------------------------------------
1 -90.000000 50.000000 0.000000 0.000000
2 0.000000 500.000000 -90.000000 0.000000
3 90.000000 0.000000 90.000000 50.000000
4 -90.000000 0.000000 0.000000 550.000000
5 90.000000 0.000000 0.000000 0.000000
6 0.000000 0.000000 0.000000 100.000000
[4] Optimized SDH Parameters:
Joint Alpha(deg) a(mm) theta(deg) d(mm)
------------------------------------------------------------------------
1 -89.976980 50.072944 0.000000 0.000000
2 0.021435 499.915919 -90.052042 0.000000
3 90.007793 -0.258274 90.043030 50.250723
4 -90.017136 0.022018 0.113726 549.979965
5 90.009449 -0.008709 -0.073612 -0.016915
6 0.000000 0.000000 0.000000 100.000000
------------------------------------------------------------------------
[5] Measurement Errors (per group):
测量1:误差 = 0.026507 mm / 0.664059 mm(校准/未校准)
测量2:误差 = 0.022484 mm / 0.473525 mm(校准/未校准)
测量3:误差 = 0.048078 mm / 0.593382 mm(校准/未校准)
测量4:误差 = 0.017212 mm / 0.286039 mm(校准/未校准)
测量5:误差 = 0.027732 mm / 0.647841 mm(校准/未校准)
测量6:误差 = 0.032805 mm / 0.217326 mm(校准/未校准)
测量7:误差 = 0.035003 mm / 0.285724 mm(校准/未校准)
测量8:误差 = 0.047712 mm / 0.182410 mm(校准/未校准)
测量9:误差 = 0.079666 mm / 0.328047 mm(校准/未校准)
测量10:误差 = 0.063394 mm / 0.456054 mm(校准/未校准)
测量11:误差 = 0.034709 mm / 0.391084 mm(校准/未校准)
测量12:误差 = 0.022172 mm / 0.455564 mm(校准/未校准)
测量13:误差 = 0.036401 mm / 0.372025 mm(校准/未校准)
测量14:误差 = 0.030719 mm / 0.494504 mm(校准/未校准)
测量15:误差 = 0.054269 mm / 0.580226 mm(校准/未校准)
测量16:误差 = 0.034244 mm / 0.375517 mm(校准/未校准)
测量17:误差 = 0.008812 mm / 0.634352 mm(校准/未校准)
测量18:误差 = 0.035747 mm / 0.420587 mm(校准/未校准)
测量19:误差 = 0.048377 mm / 0.445601 mm(校准/未校准)
测量20:误差 = 0.062382 mm / 0.520417 mm(校准/未校准)
测量21:误差 = 0.043945 mm / 0.516382 mm(校准/未校准)
测量22:误差 = 0.028854 mm / 0.294653 mm(校准/未校准)
测量23:误差 = 0.040496 mm / 0.220989 mm(校准/未校准)
测量24:误差 = 0.012670 mm / 0.412269 mm(校准/未校准)
测量25:误差 = 0.098429 mm / 0.802622 mm(校准/未校准)
测量26:误差 = 0.034564 mm / 0.312927 mm(校准/未校准)
测量27:误差 = 0.057626 mm / 0.691680 mm(校准/未校准)
测量28:误差 = 0.017561 mm / 0.374001 mm(校准/未校准)
测量29:误差 = 0.037320 mm / 0.463712 mm(校准/未校准)
测量30:误差 = 0.050038 mm / 0.525567 mm(校准/未校准)
测量31:误差 = 0.038108 mm / 0.874976 mm(校准/未校准)
测量32:误差 = 0.046431 mm / 0.425734 mm(校准/未校准)
测量33:误差 = 0.027192 mm / 0.575715 mm(校准/未校准)
测量34:误差 = 0.016891 mm / 0.355442 mm(校准/未校准)
测量35:误差 = 0.048557 mm / 0.327223 mm(校准/未校准)
测量36:误差 = 0.056675 mm / 0.637538 mm(校准/未校准)
测量37:误差 = 0.069998 mm / 0.400602 mm(校准/未校准)
测量38:误差 = 0.086267 mm / 0.289902 mm(校准/未校准)
测量39:误差 = 0.021268 mm / 0.472069 mm(校准/未校准)
测量40:误差 = 0.035523 mm / 0.566289 mm(校准/未校准)
测量41:误差 = 0.035594 mm / 0.565018 mm(校准/未校准)
测量42:误差 = 0.036709 mm / 0.637583 mm(校准/未校准)
测量43:误差 = 0.026452 mm / 0.207000 mm(校准/未校准)
测量44:误差 = 0.024210 mm / 0.485523 mm(校准/未校准)
测量45:误差 = 0.051299 mm / 0.372913 mm(校准/未校准)
测量46:误差 = 0.053558 mm / 0.368482 mm(校准/未校准)
测量47:误差 = 0.036068 mm / 0.304884 mm(校准/未校准)
测量48:误差 = 0.022227 mm / 0.426705 mm(校准/未校准)
测量49:误差 = 0.045959 mm / 0.338290 mm(校准/未校准)
测量50:误差 = 0.064172 mm / 0.386015 mm(校准/未校准)
测量51:误差 = 0.026428 mm / 0.523266 mm(校准/未校准)
测量52:误差 = 0.017636 mm / 0.647093 mm(校准/未校准)
测量53:误差 = 0.022520 mm / 0.511791 mm(校准/未校准)
测量54:误差 = 0.032559 mm / 0.265368 mm(校准/未校准)
测量55:误差 = 0.031090 mm / 0.471388 mm(校准/未校准)
测量56:误差 = 0.031606 mm / 0.795395 mm(校准/未校准)
测量57:误差 = 0.036189 mm / 0.473452 mm(校准/未校准)
测量58:误差 = 0.035285 mm / 0.610204 mm(校准/未校准)
测量59:误差 = 0.055424 mm / 0.681401 mm(校准/未校准)
测量60:误差 = 0.027973 mm / 0.540605 mm(校准/未校准)
[6]校准结果统计(位置误差,单位:mm)
mean max 90%max σ 6σ number_of_points
------------------------------------------------------------------------------
校准前 0.466283 0.874976 0.647841 0.152851 0.917108 60
校准后 0.039163 0.098429 0.062382 0.017692 0.106153 60示例,accuracy_stats_hist_TX2-90L.png如下:
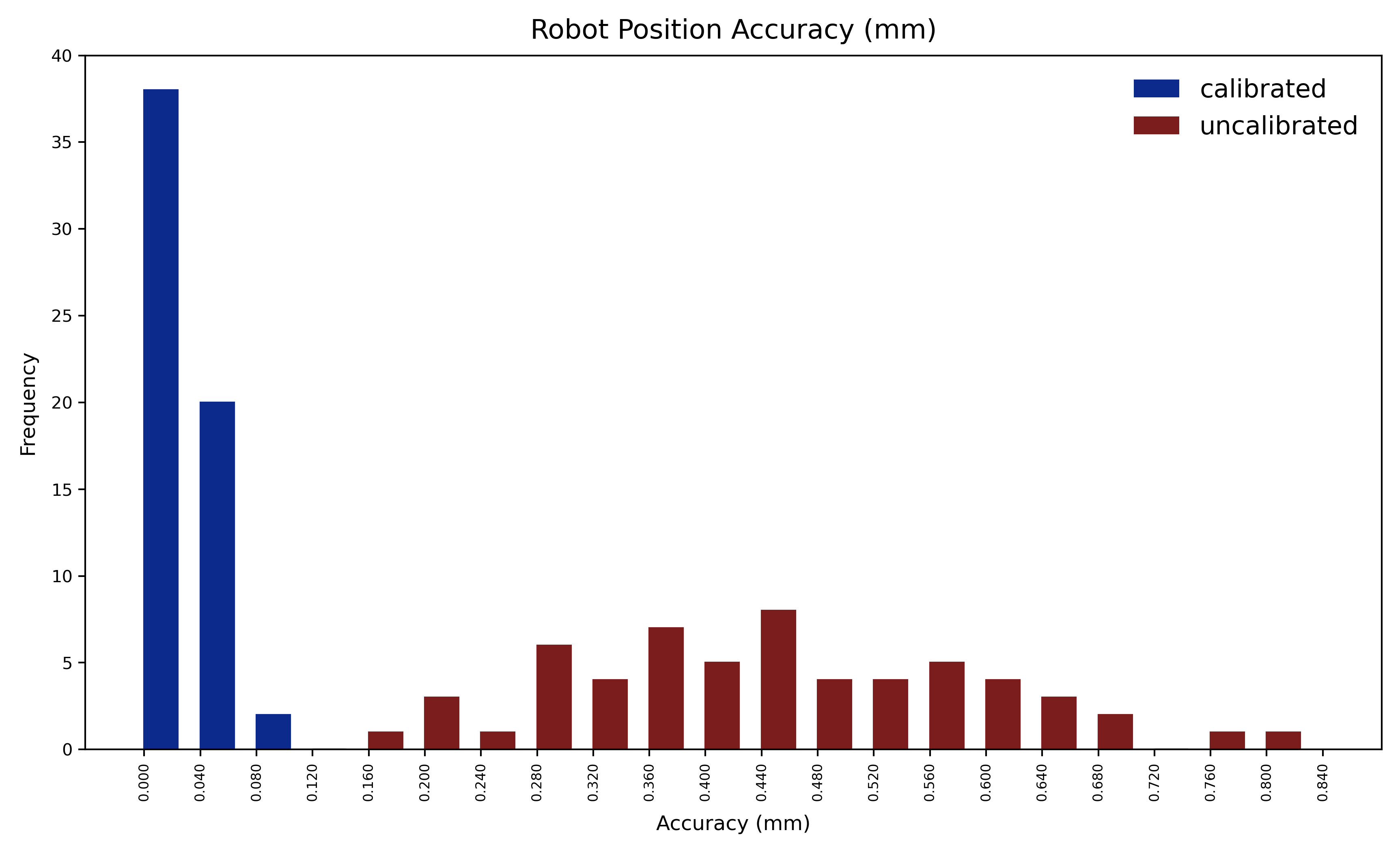
手动生成直方图(可自定义输入报告路径):
bash
python3 code/scripts/visualize_optimal_report.py results/TX200/OptimalReport_TX200.txt演示平面法向与法向可视化(示例脚本):
bash
python3 code/scripts/visualize_normal_plane.pyDocker(可选)
如需在容器内复现实验:
bash
# 构建
docker build -t robotcalib -f docker/Dockerfile .
# 运行(挂载当前工程,启用多核)
docker run --rm -it robotcalib \
bash -lc "mkdir build && cd build && cmake .. && make -j8 && ./build/RobotCalibration TX2-90L complete"如需导出图片到宿主机,确保将
results/目录挂载到宿主机路径。
技术服务
机械臂绝对精度/外参校准实战落地:提供线下的校准服务与线上的全量资料包 (原理说明+完整代码+实测数据+软件操作+一线经验)。线上可持续答疑。
可选的机械臂校准资料包
线上的全量资料包(原理说明+完整代码+实测数据+软件操作+一线经验)包括以下所有内容:
powershell
$ tree
.
├── 代码
│ └── RobotCalib
│ ├── CMakeLists.txt
│ ├── README.md
│ ├── code
│ │ ├── include
│ │ │ ├── core
│ │ │ │ ├── BaseCalib.hpp
│ │ │ │ ├── NormalCrossCompute.h
│ │ │ │ ├── RobotCalib.h
│ │ │ │ └── ToolCalib.hpp
│ │ │ └── tools
│ │ │ ├── DataReader.h
│ │ │ ├── DataStas.h
│ │ │ ├── Forward.h
│ │ │ └── MatrixCompute.h
│ │ ├── scripts
│ │ │ ├── visualize_normal_plane.py
│ │ │ └── visualize_optimal_report.py
│ │ └── source
│ │ ├── core
│ │ │ ├── NormalCrossCompute.cpp
│ │ │ └── RobotCalib.cpp
│ │ ├── main.cpp
│ │ └── tools
│ │ ├── DataReader.cpp
│ │ ├── DataStas.cpp
│ │ └── MatrixCompute.cpp
│ ├── config
│ │ ├── DH
│ │ │ ├── TX2-90L-default.yml
│ │ │ └── TX200-default.yml
│ │ ├── measured
│ │ │ ├── TX2-90L
│ │ │ │ ├── TX2-90L_绝对精度验证结果(测试集).xlsx
│ │ │ │ ├── 机器人校准-BaseSetup.csv
│ │ │ │ ├── 机器人校准-Calibration.csv
│ │ │ │ └── 机器人校准-ToolSetup.csv
│ │ │ └── TX200
│ │ │ ├── TX200_绝对精度验证结果(测试集).xlsx
│ │ │ ├── 机器人校准-BaseSetup.csv
│ │ │ ├── 机器人校准-Calibration.csv
│ │ │ └── 机器人校准-ToolSetup.csv
│ │ └── option
│ │ ├── CalibConfigComplete.yml
│ │ └── CalibConfigSimple.yml
│ ├── doc
│ │ ├── TX2-90L
│ │ │ ├── AbsoluteCalibrationQualityReport_TX2-90L.pdf
│ │ │ ├── RoboDK校准报告-TX2-90L.pdf
│ │ │ ├── RoboD校准位置精度截图-TX2-90L.png
│ │ │ ├── TX2-90L简介.png
│ │ │ └── 原厂校准位置精度截图-TX2-90L.png
│ │ ├── TX200
│ │ │ ├── AbsoluteCalibrationQualityReport_TX200.pdf
│ │ │ ├── RoboDK校准报告-TX200.pdf
│ │ │ ├── RoboDK校准位置精度截图-TX200.png
│ │ │ ├── TX200简介.png
│ │ │ └── 原厂校准位置精度截图-TX200.png
│ │ └── 计算共垂线的算法原理.md
│ ├── docker
│ │ └── Dockerfile
│ └── results
│ ├── TX2-90L
│ │ ├── OptimalReport_TX2-90L.txt
│ │ └── accuracy_stats_hist_TX2-90L.png
│ └── TX200
│ ├── OptimalReport_TX200.txt
│ └── accuracy_stats_hist_TX200.png
└── 文档
├── robodk软件使用说明
│ └── robodk进行机械臂校准的流程.vsdx
├── 校准原理说明
│ └── 工业六轴机械臂标定校准原理说明.docx
└── 高级工程师经验分享
└── staubli机械臂标定校准实施标准操作流程(真实工作经历吐血总结).docx
28 directories, 49 files
(base) 
