leetcode 6 Z字形变化

一、题目描述

二、解题思路

解法一

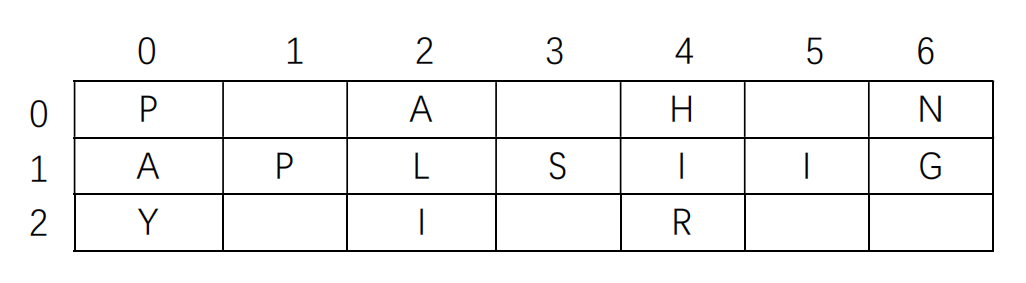
构造二维向量，模拟Z字填写。实例填写后的二维向量如图所示：

解法二

整体思路

根据解法一模拟过程，寻找下标规律 。

具体思路

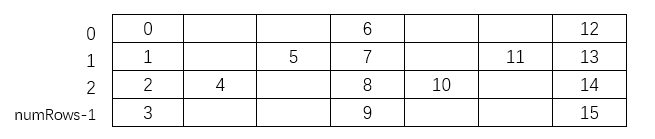
例如，当numRows=4时，通过观察每一行下标之间的关系我们可以知道：

(1)第0行和第numRows行后一个下标与前一个下标的差为2*numRows-2，设这个值为d(公差)，

下标规律为：

k，k+d，k+2d，k+3d......

(2)中间第k行可以两个组成一组，其下标规律为：

(k，d-k)，(k+d，（d-k）+d)，（k+2d，（d-k）+2d）......

三、代码实现

解法一

时间复杂度：T(n)=O(m*n)

空间复杂度：S(n)=O(m*n)

cpp 复制代码

class Solution {
public:
    string convert(string s, int numRows) {
        //边界处理
        if(numRows==1||s.size()<=numRows) return s;
        //申请二维向量,模拟Z字填写
        vector<vector<char>> z_board(numRows,vector<char>(s.size(),'0'));
        //填写二维向量
        int num=0,row=0,line=0;
        while(num!=s.size()){
            //向下填写
            while(row<numRows&&num!=s.size()){
                z_board[row][line]=s[num];
                num++;row++;
            }
            row-=2;line++;
            //向右上填写
            while(row>0&&num!=s.size()){
                z_board[row][line]=s[num];
                num++;row--;line++;
            }
        }
        //构造需要返回的字符串
        string ret;
        for(int i=0;i!=numRows;i++)
            for(int j=0;j!=s.size();j++)
                if(z_board[i][j]!='0')
                    ret+=z_board[i][j];
        return ret;
    }
};

解法二

时间复杂度：T(n)=O(n)

空间复杂度：S(n)=O(1)

cpp 复制代码

class Solution {
public:
    string convert(string s, int numRows) {
        //根据模拟填写，观察下标规律
        //边界处理
        if(numRows==1||s.size()<=numRows) return s;
        //计算公差d
       int d=2*numRows-2;
       string ret;
       for(int row=0;row!=numRows;row++){
        //如果为第0行或者第numRows-1行
        if(row==0||row==numRows-1)
            for(int left=row;left<s.size();left+=d)
                ret+=s[left];
        //如果为中间第k行
        else {
            for(int left=row,right=d-row;left<s.size()||right<s.size();left+=d,right+=d){
                if(left<s.size())
                    ret+=s[left];
                if(right<s.size())
                    ret+=s[right];
            } 
        }
       }
       return ret;
    }
};