《sklearn机器学习——聚类性能指标》Silhouette 系数

轮廓系数 (Silhouette Coefficient) 简介

轮廓系数（Silhouette Coefficient）是一种用于评估聚类算法性能的内部指标 ，它不需要真实的类别标签，仅根据数据本身的聚类结果来衡量聚类的质量。该指标能够同时反映聚类的凝聚度 （Cohesion，簇内紧密性）和分离度（Separation，簇间分离性）。

1. 核心思想

轮廓系数的基本思想是：一个好的聚类结果应该满足：

簇内紧密：同一个簇内的数据点彼此之间距离很近。
簇间分离：不同簇的数据点彼此之间距离较远。

对于每一个数据点，轮廓系数通过比较它与自身所在簇内其他点 的平均距离（a）和它与最近的其他簇中所有点的平均距离（b），来量化该点的"聚类合理性"。

2. 计算方法

2.1 单个样本的轮廓系数

对于一个数据点 i i i，其轮廓系数 s ( i ) s(i) s(i) 定义如下：

s ( i ) = b ( i ) − a ( i ) max ⁡ { a ( i ) , b ( i ) } s(i) = \frac{b(i) - a(i)}{\max\{a(i), b(i)\}} s(i)=max{a(i),b(i)}b(i)−a(i)

其中：

a ( i ) a(i) a(i)：样本 i i i 到其所在簇内所有其他样本的平均距离。这衡量了凝聚度 ， a ( i ) a(i) a(i) 越小越好。
b ( i ) b(i) b(i)：样本 i i i 到最近的其他簇 中所有样本的平均距离。这衡量了分离度 ， b ( i ) b(i) b(i) 越大越好。

2.2 轮廓系数的取值范围

+1 : 表示样本 i i i 被分配到了正确的簇，且远离其他簇。这是理想情况。
0 : 表示样本 i i i 在两个簇的边界上，聚类结果不明确。
-1 : 表示样本 i i i 可能被分配到了错误的簇，它更接近于另一个簇。

2.3 整个数据集的轮廓系数

整个数据集的轮廓系数是所有样本轮廓系数的平均值：

Silhouette Score = 1 N ∑ i = 1 N s ( i ) \text{Silhouette Score} = \frac{1}{N} \sum_{i=1}^{N} s(i) Silhouette Score=N1i=1∑Ns(i)

其中 N N N 是样本总数。

3. 特点

内部指标: 无需真实标签，适用于无监督学习的评估。
取值范围: [-1, 1]，值越大表示聚类效果越好。
直观解释: 可以为每个样本计算轮廓系数，便于进行可视化分析（如轮廓图）。
对簇形状敏感: 假设簇是凸形的（如球形），对于非凸形状的簇（如环形、月牙形）效果可能不佳。
对簇数量的指导 : 常用于确定最优的聚类数量 k k k。通常选择使轮廓系数最大的 k k k 值。

4. 与其他指标的比较

指标	类型	是否需要真实标签	优点	缺点
轮廓系数	内部	否	无需标签，直观，可指导选择k	对非凸簇效果差，计算复杂度较高
Fowlkes-Mallows 得分	外部	是	有明确的上下界，基于成对比较	需要真实标签
Calinski-Harabasz 指数	内部	否	计算快，常用于选择k	数值本身无界，解释性稍差
Davies-Bouldin 指数	内部	否	越小越好，物理意义明确	越小越好，与其他指标方向相反

5. 内部数学形式

如果真实簇标签不知道，则必须使用模型本身进行度量。Silhouette 系数 (sklearn.metrics.silhouette_score) 这种度量的一个示例，其中较高的 Silhouette 系数得分和具有更好定义的聚类的模型有关。Silhouette 系数根据每个样本进行定义，由两个得分组成:

a a a: 样本与同一类别中所有其他点之间的平均距离。
b b b: 样本与下一个距离最近的簇中的所有其他点之间的平均距离。

给出单个样本的 Silhouette 系数 ( s ) ( s ) (s):

s = b − a max ⁡ ( a , b ) s = \frac{b - a}{\max(a, b)} s=max(a,b)b−a

其中每个样本的 Silhouette 系数的平均值可以使用一组样本的 Silhouette 系数。

轮廓系数 (Silhouette Coefficient) 的优点与缺点

轮廓系数是一种广泛使用的聚类评估指标，它通过量化每个数据点在聚类中的"合理性"来评估整体聚类质量。以下是其主要的优点和缺点：

优点

无需真实标签（无监督评估）：
- 轮廓系数是一个内部评估指标，它仅依赖于数据点之间的距离和聚类结果本身，不需要真实的类别标签。这使得它在绝大多数实际的无监督聚类场景中非常实用。
直观且可解释性强：
- 其取值范围在 [-1, 1] 之间，含义清晰：
  - 接近 1：表示样本被分配到了正确的簇，且远离其他簇。
  - 接近 0：表示样本位于两个簇的边界上，聚类结果不明确。
  - 接近 -1：表示样本很可能被分配到了错误的簇。
- 这种直观的解释使得结果易于理解和沟通。
可进行样本级分析和可视化：
- 可以为每一个数据点 计算轮廓系数，这使得我们可以：
  - 绘制轮廓图 (Silhouette Plot)，直观地展示每个簇的轮廓系数分布。
  - 识别出聚类效果不佳的特定样本或簇（例如，轮廓系数为负或接近0的样本）。
  - 分析哪些簇的凝聚度高，哪些簇的分离度不够。
同时衡量凝聚度和分离度：
- 轮廓系数的计算同时考虑了簇内距离 （a(i)，凝聚度）和簇间距离（b(i)，分离度），能够综合反映聚类的质量。
可用于确定最优聚类数 (k)：
- 这是轮廓系数最经典的应用之一。通过计算不同聚类数量 k 下的平均轮廓系数，并选择使轮廓系数最大的 k 值，可以作为确定最优簇数量的有效方法。

缺点

对非凸形状的簇效果不佳：
- 轮廓系数基于欧氏距离 和平均距离 ，它假设簇是凸形的（如球形、椭球形）。
- 对于非凸形状的簇（例如，环形、月牙形、带状等），轮廓系数可能会给出较低的评分，即使这些簇在几何上是合理的。它倾向于发现球形的簇。
计算复杂度较高：
- 计算轮廓系数需要计算所有数据点之间的成对距离，其时间复杂度通常为 O(n²) ，其中 n 是样本数量。
- 对于大规模数据集，计算轮廓系数可能会非常耗时。
对密度差异大的簇敏感：
- 当簇的密度差异很大时（例如，一个簇非常密集，另一个簇非常稀疏），基于平均距离的计算可能会失真，导致评估结果不准确。
可能偏向于数量较多的簇：
- 在某些情况下，增加簇的数量 k 会人为地降低簇内平均距离 a(i)，从而可能提高轮廓系数，但这并不一定意味着聚类结果在语义上更好。需要结合业务背景谨慎解读。
数值解释的局限性：
- 虽然轮廓系数有明确的范围，但一个"好"的轮廓系数值是多少并没有绝对标准。例如，0.5 可能对于某些数据集已经是很好的结果，而对于另一些数据集则可能很差。

总结

轮廓系数是一个强大且直观的聚类评估工具，尤其适合用于选择最优聚类数 和进行聚类结果的可视化诊断 。然而，使用时必须注意其局限性，特别是它对簇的形状假设 和计算开销。在实际应用中，建议结合其他指标（如 Calinski-Harabasz 指数）和领域知识，对聚类结果进行综合评估。

轮廓系数的使用场景与 Python 示例

使用场景

轮廓系数在聚类分析中有两个最典型的应用场景：

1. 确定最优聚类数量 (k)

这是轮廓系数最经典和最有价值的用途。当使用如 K-Means 这样的算法时，需要预先指定簇的数量 k。轮廓系数可以帮助我们找到使聚类效果最优的 k 值。

方法：

尝试一系列不同的 k 值（例如，从 2 到 10）。
对每个 k 值运行聚类算法并计算轮廓系数。
选择使平均轮廓系数最大 的 k 值。

2. 评估和诊断聚类质量

轮廓系数不仅可以给出一个整体分数，还可以为每个样本提供一个分数，这使得我们可以：

评估整体质量：通过平均轮廓系数判断当前聚类结果的好坏。
可视化分析：绘制轮廓图（Silhouette Plot），直观地查看每个簇的轮廓系数分布，识别出聚类效果不佳的簇或异常样本。

Python 示例

以下代码演示了如何使用 scikit-learn 计算轮廓系数，并用于确定最优的聚类数量。

python 复制代码

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score, silhouette_samples
import matplotlib.cm as cm

# 1. 生成示例数据
X, y_true = make_blobs(n_samples=500,
                       centers=4,
                       cluster_std=0.9,
                       center_box=(-10.0, 10.0),
                       shuffle=True,
                       random_state=42)

# 2. 场景一：确定最优聚类数量 (k)
print("计算不同 k 值下的轮廓系数...")
k_range = range(2, 11)
silhouette_scores = []

for k in k_range:
    kmeans = KMeans(n_clusters=k, random_state=42, n_init=10)
    cluster_labels = kmeans.fit_predict(X)
    score = silhouette_score(X, cluster_labels)
    silhouette_scores.append(score)
    print(f"k={k}: 轮廓系数 = {score:.3f}")

# 绘制轮廓系数随 k 的变化图
plt.figure(figsize=(14, 5))

plt.subplot(1, 2, 1)
plt.plot(k_range, silhouette_scores, 'bo-')
plt.xlabel('聚类数量 k')
plt.ylabel('轮廓系数')
plt.title('轮廓系数 vs 聚类数量 k')
plt.grid(True)
optimal_k = k_range[np.argmax(silhouette_scores)]
plt.axvline(x=optimal_k, color='r', linestyle='--', label=f'最优 k = {optimal_k}')
plt.legend()

# 3. 场景二：绘制轮廓图 (k=4)
k = 4
kmeans = KMeans(n_clusters=k, random_state=42, n_init=10)
cluster_labels = kmeans.fit_predict(X)

# 计算每个样本的轮廓系数
sample_silhouette_values = silhouette_samples(X, cluster_labels)
avg_score = silhouette_score(X, cluster_labels)

plt.subplot(1, 2, 2)
y_lower = 10
colors = cm.tab10(np.linspace(0, 1, k))

for i in range(k):
    # 提取第 i 个簇的轮廓系数并排序
    ith_cluster_silhouette_values = sample_silhouette_values[cluster_labels == i]
    ith_cluster_silhouette_values.sort()

    size_cluster_i = ith_cluster_silhouette_values.shape[0]
    y_upper = y_lower + size_cluster_i

    plt.fill_betweenx(np.arange(y_lower, y_upper),
                      0, ith_cluster_silhouette_values,
                      facecolor=colors[i], edgecolor=colors[i], alpha=0.7)

    plt.text(-0.05, y_lower + 0.5 * size_cluster_i, str(i))
    y_lower = y_upper + 10  # 10 for the 0 samples

plt.xlabel('轮廓系数')
plt.ylabel('簇标签')
plt.title(f'轮廓图 (k={k}, 平均轮廓系数={avg_score:.3f})')

# 画出平均轮廓系数的垂直线
plt.axvline(x=avg_score, color="red", linestyle="--", label=f'平均值 = {avg_score:.3f}')
plt.legend()
plt.yticks([])  # 清除 y 轴刻度
plt.tight_layout()
plt.show()

print(f"\n结论：根据轮廓系数，最优聚类数量 k = {optimal_k}")

输出：

python 复制代码

计算不同 k 值下的轮廓系数...
k=2: 轮廓系数 = 0.601
k=3: 轮廓系数 = 0.772
k=4: 轮廓系数 = 0.812
k=5: 轮廓系数 = 0.682
k=6: 轮廓系数 = 0.550
k=7: 轮廓系数 = 0.449
k=8: 轮廓系数 = 0.347
k=9: 轮廓系数 = 0.347
k=10: 轮廓系数 = 0.358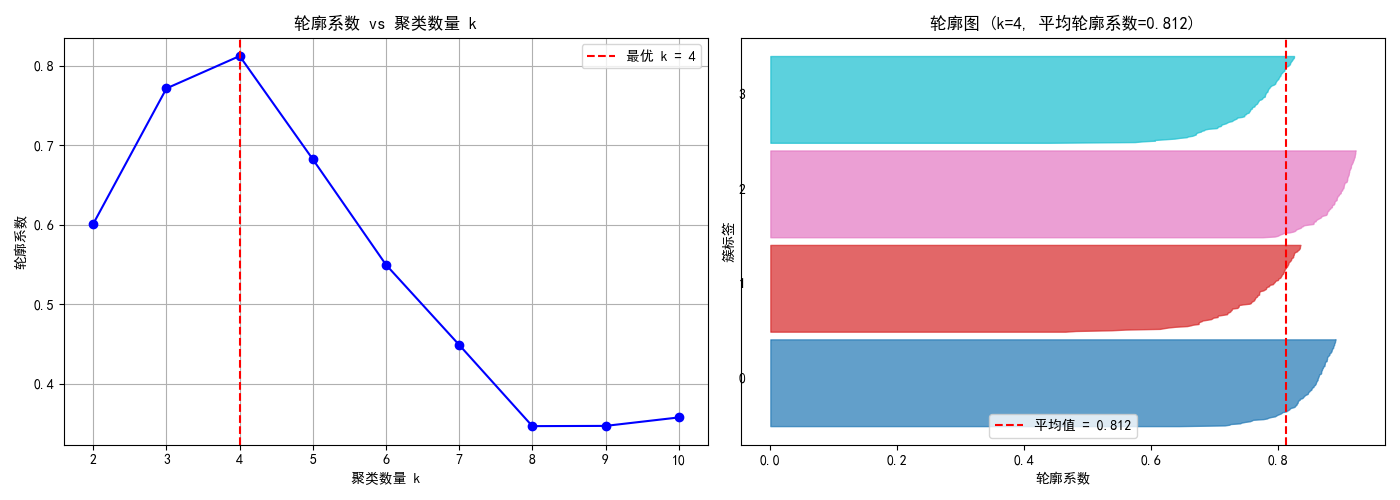

输出解读

左图：显示了不同 k 值下的轮廓系数。峰值通常对应最优的 k 值。

右图（轮廓图）：

每个水平条带代表一个簇。

条带越长（向右延伸越多），表示该簇的样本轮廓系数越高，聚类效果越好。

如果条带长度差异很大，或者有负值，说明聚类效果可能不理想。

通过这个示例，可以清晰地看到轮廓系数如何帮助我们选择 k 和诊断聚类结果。

总结

Fowlkes-Mallows 得分 是衡量聚类"准确性"的黄金标准（当有真值时）。
轮廓系数 是探索聚类"合理性 "和"有效性"的强大工具（尤其在无真值时）。

在实际应用中，应根据手头的数据和分析目标选择合适的指标。理想情况下，可以结合多个指标（如轮廓系数、Calinski-Harabasz 指数等）进行综合判断，以获得对聚类结果更全面、更稳健的评估。