集成学习 —— 梯度提升树GBDT、XGBoost

目录

一、梯度提升树

[1、残差提升树 Boosting Decision Tree](#1、残差提升树 Boosting Decision Tree)

[2、梯度提升树 Gradient Boosting Decision Tree](#2、梯度提升树 Gradient Boosting Decision Tree)

二、构建案例

[1、 初始化弱学习器(CART树)：](#1、 初始化弱学习器(CART树)：)

[2、 构建第1个弱学习器](#2、 构建第1个弱学习器)

[3、 构建第2个弱学习器](#3、 构建第2个弱学习器)

[4、 构建第3个弱学习器](#4、 构建第3个弱学习器)

[5、 构建最终弱学习器](#5、 构建最终弱学习器)

[6、 构建总结](#6、 构建总结)

三、XGBoost

一、梯度提升树

1、残差提升树 Boosting Decision Tree

思想：通过拟合残差的思想来进行提升，残差：真实值 - 预测值

例如：

2、梯度提升树 Gradient Boosting Decision Tree

梯度提升树不再拟合残差，而是利用梯度下降的近似方法，利用损失函数的负梯度作为提升树算法中的残差近似值。

GBDT 拟合的负梯度就是残差。如果我们的 GBDT 进行的是分类问题，则损失函数变为 logloss，此时拟合的目标值就是该损失函数的负梯度值。

二、构建案例

已知：

1、 初始化弱学习器(CART树)：

当模型预测值为何值时，会使得第一个弱学习器的平方误差最小，即：求损失函数对 f(xi) 的导数，并令导数为0。

2、 构建第1个弱学习器

根据负梯度的计算方法得到下表：

以此类推，计算所有切分点情况，得到：

由此得到，当 6.5 作为切分点时，平方损失最小，此时得到第1棵决策树。

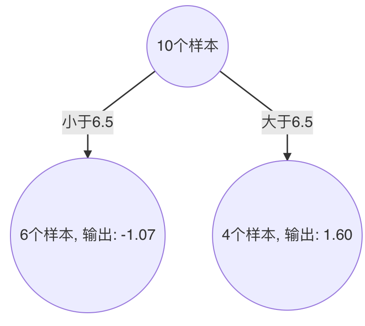
3、 构建第2个弱学习器

以此类推，计算所有切分点情况，得到：

以3.5 作为切分点时，平方损失最小，此时得到第2棵决策树

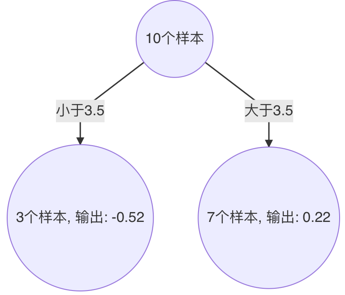
4、 构建第3个弱学习器

以此类推，计算所有切分点情况，得到：

以6.5 作为切分点时，平方损失最小，此时得到第3棵决策树

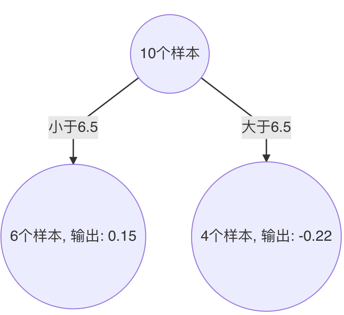
5、 构建最终弱学习器

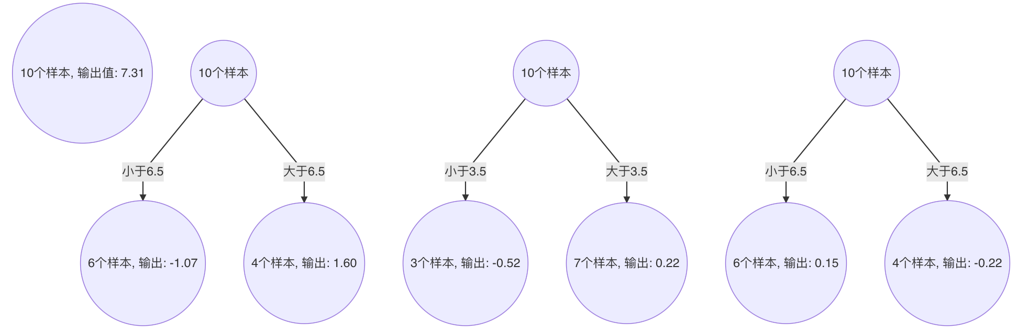
以 x=6 样本为例：输入到最终学习器中的结果 ：（存在误差，说明学习器不够）

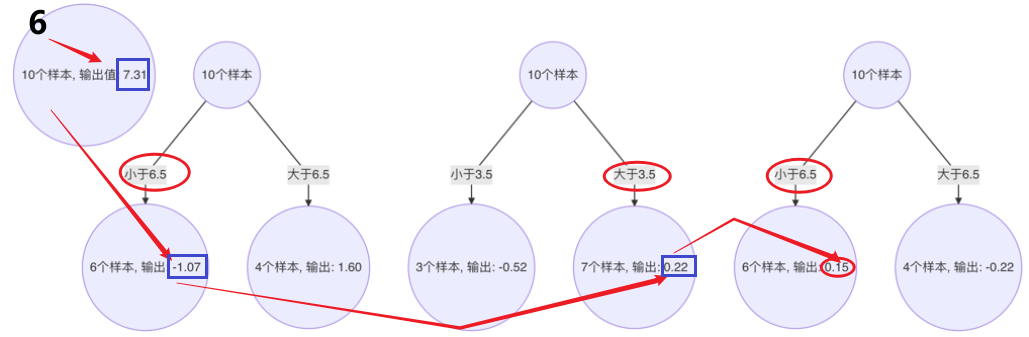
以此类推计算其他的预测值

6、 构建总结

1. 初始化弱学习器（目标值的均值作为预测值）
2. 迭代构建学习器，每一个学习器拟合上一个学习器的负梯度
3. 直到达到指定的学习器个数
4. 当输入未知样本时，将所有弱学习器的输出结果组合起来作为强学习器的输出

三、XGBoost

待补充..........