决策树简介
决策树是一种树形结构
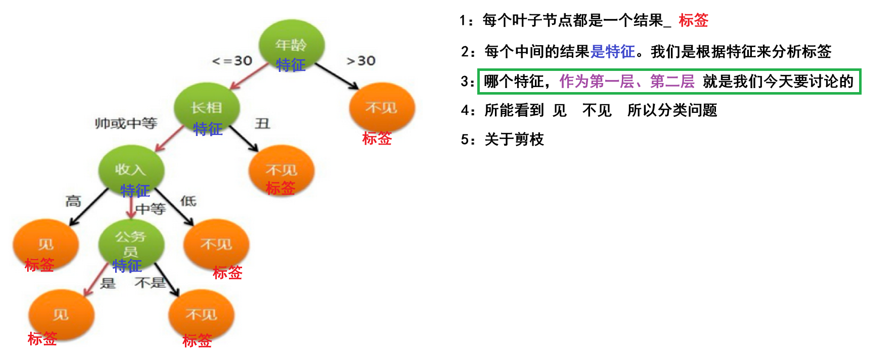
树中每个内部节点表示一个特征上的判断，每个分支代表一个判断结果的输出，每个叶子节点代表一种分类结果
(仅举例无其他意义或隐喻)就像一个女孩去相亲，那么首先询问是否大于30，大于则不见，不大于再看外貌条件，不丑则在看收入条件等。这些选择就是这棵树的特征
决策树的建立过程
1.特征选择：选取有较强分类能力的特征。
2.决策树生成：根据选择的特征生成决策树。
- 决策树也易过拟合，采用剪枝的方法缓解过拟合
然后我们引入一个特殊的概念：
信息熵
熵 Entropy ：信息论中代表随机变量不确定度的度量
熵越大，数据的不确定性度越高，信息就越多
熵越小，数据的不确定性越低
信息熵的计算方法
例如
信息增益
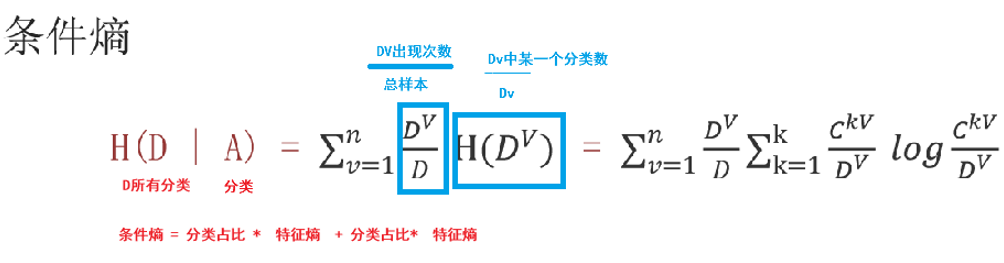
公式有点难看明白，所以来看个例子8:
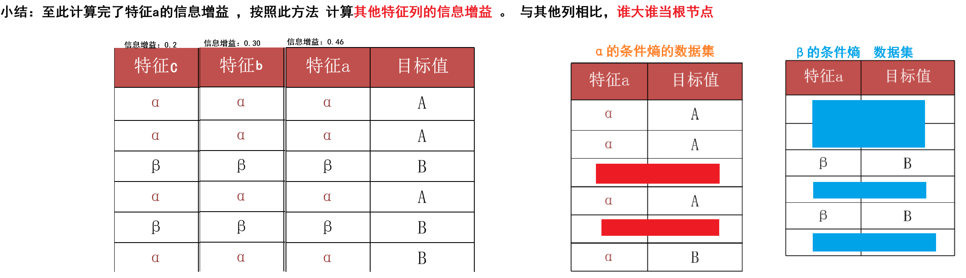
了解完熵之后，就可以看后面的了
ID3决策树
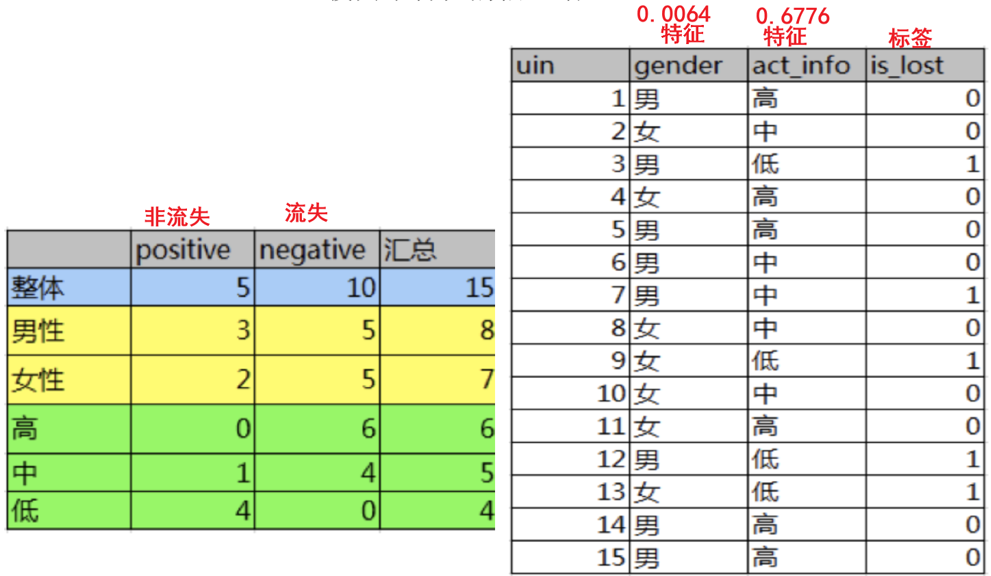
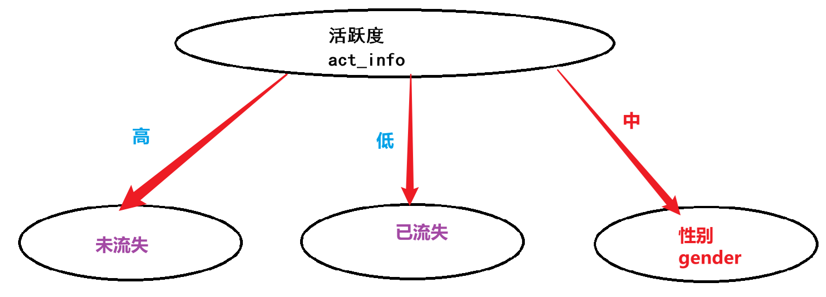
接下来还要了解一些信息增益率
信息增益率 = 信息增益 /特征熵
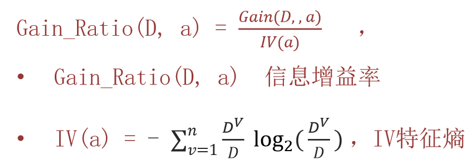
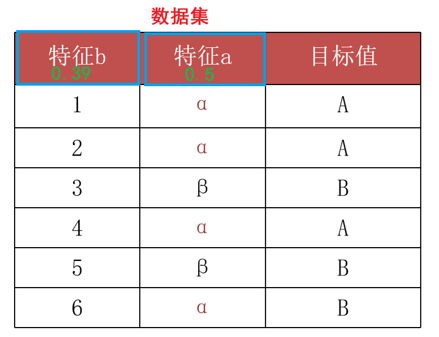
求特征a、b的信息增益率
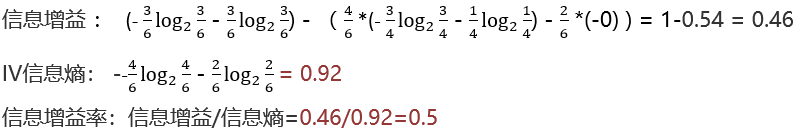
CART树
**基尼值Gini（D）：**从数据集D中随机抽取两个样本，其类别标记不一致的概率。故，Gini（D）值越小，数据集D****的纯度越高
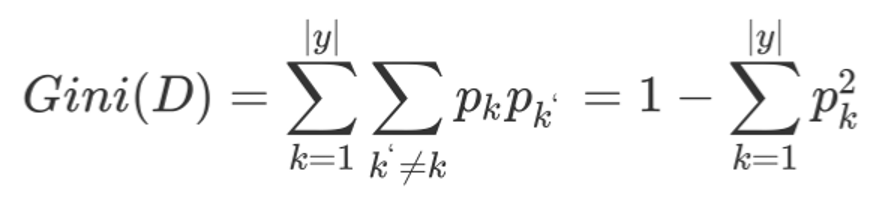**基尼指数Gini_index（D）：**选择使划分后基尼系数最小的属性作为最优化分属性。
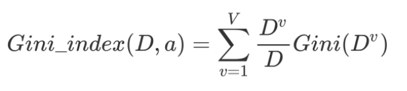
例子
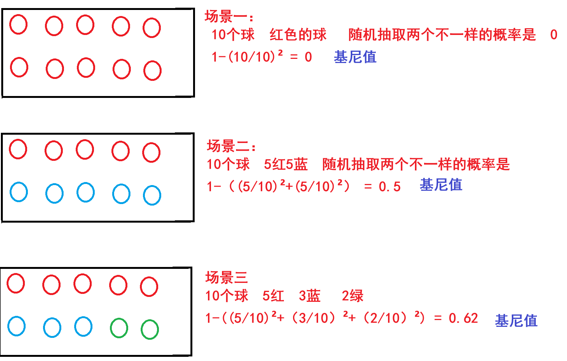
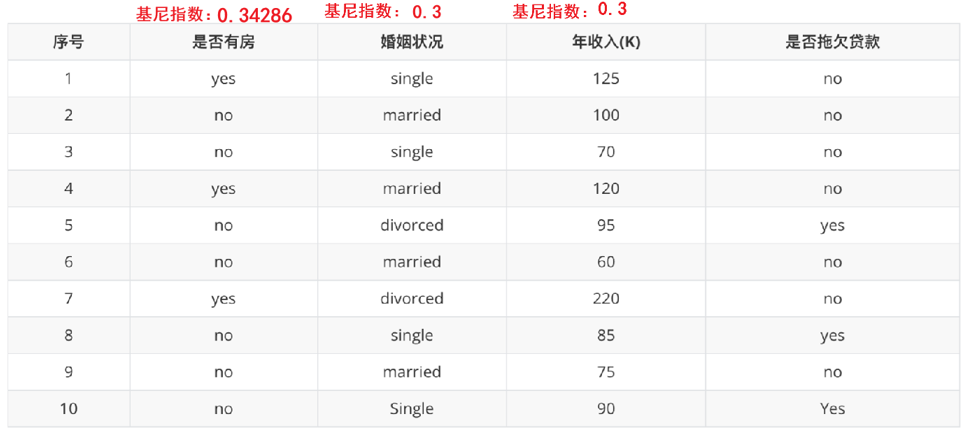
CRAT分类树
已知：是否拖欠贷款数据。
需求：计算各特征的基尼指数，选择最优分裂点
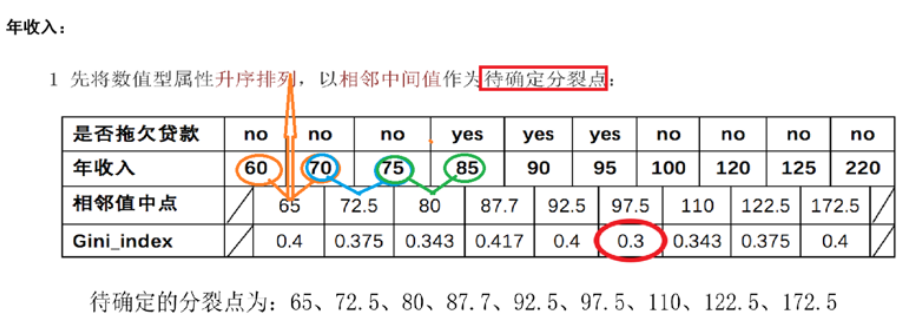
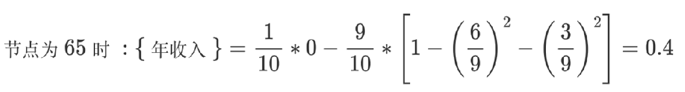
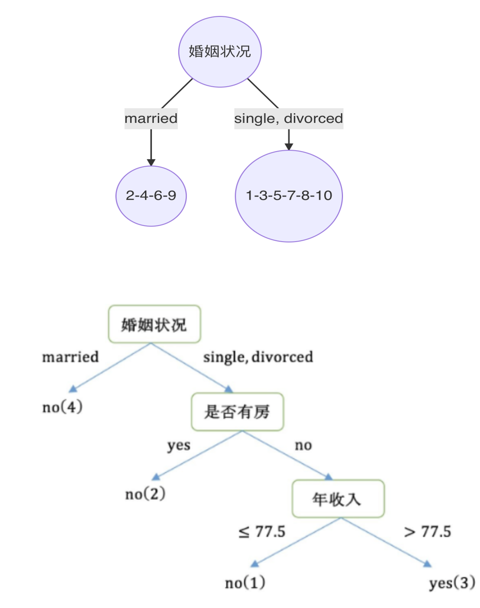
CART回归树
平方损失
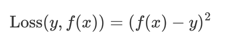
根据平方损失构建CART回归树
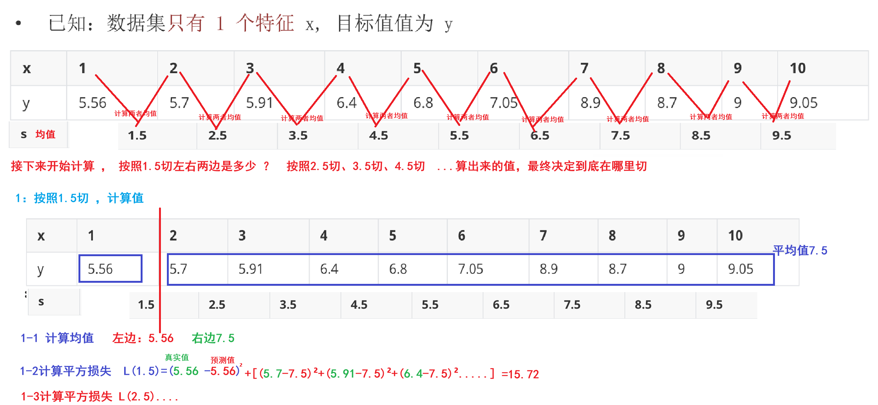
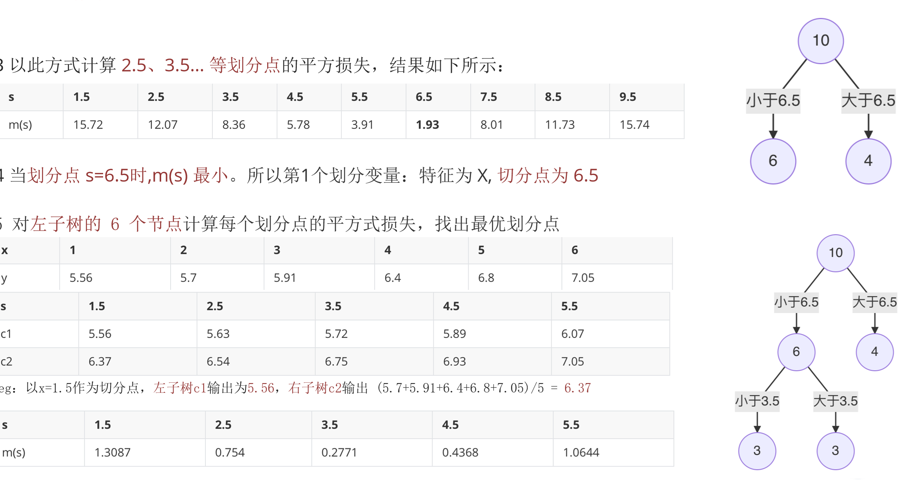
但是实际使用中回归问题还是用线性回归来做，决策树容易过拟合
python
"""
结论：
回归类的问题。即能使用线性回归，也能使用决策树回归
优先使用线性回归，因为决策树回归可能比较容易导致过拟合
"""
import numpy as np
import pandas as pd
from sklearn.tree import DecisionTreeRegressor #回归决策树
from sklearn.linear_model import LinearRegression #线性回归
import matplotlib.pyplot as plt
#1、获取数据
x = np.array(list(range(1, 11))).reshape(-1, 1)
y = np.array([5.56, 5.70, 5.91, 6.40, 6.80, 7.05, 8.90, 8.70, 9.00, 9.05])
#2、创建线性回归 和 决策树回归
es1=LinearRegression()
es2=DecisionTreeRegressor(max_depth=1)
es3=DecisionTreeRegressor(max_depth=10)
#3、模型训练
es1.fit(x,y)
es2.fit(x,y)
es3.fit(x,y)
#4、准备测试数据 ，用于测试
# 起始, 结束, 步长.
x_test = np.arange(0.0, 10.0, 0.1).reshape(-1, 1)
print(x_test)
#5、模型预测
y_predict1=es1.predict(x_test)
y_predict2=es2.predict(x_test)
y_predict3=es3.predict(x_test)
#6、绘图
plt.figure(figsize=(10,5))
#散点图
plt.scatter(x,y,color='gray',label='data')
plt.plot(x_test,y_predict1,color='g',label='liner regression')
plt.plot(x_test,y_predict2,color='b',label='max_depth=1')
plt.plot(x_test,y_predict3,color='r',label='max_depth=10')
plt.legend()
plt.xlabel("data")
plt.ylabel("target")
plt.show()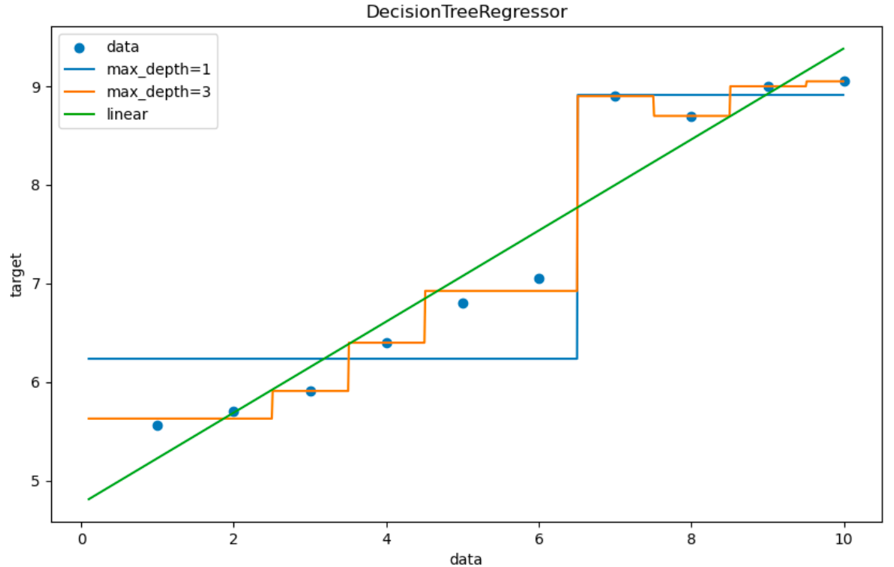
决策树剪枝
决策树剪枝是一种防止决策树过拟合的一种正则化方法；提高其泛化能力。
把子树的节点全部删掉，使用用叶子节点来替换
1.预剪枝：指在决策树生成过程中，对每个节点在划分前先进行估计，若当前节点的划分不能带来决策树泛化性能提升，则停止划分并将当前节点标记为叶节点;
优点：
预剪枝使决策树的很多分支没有展开，不单降低了过拟合风险，还显著减少了决策树的训练、测试时间开销
缺点：
有些分支的当前划分虽不能提升泛化性能，但后续划分却有可能导致性能的显著提高；
预剪枝决策树也带来了欠拟合的风险
2.后剪枝：是先从训练集生成一棵完整的决策树，然后自底向上地对非叶节点进行考察，若将该节点对应的子树替换为叶节点能带来决策树泛化性能提升，则将该子树替换为叶节点。
优点：比预剪枝保留了更多的分支。一般情况下，后剪枝决策树的欠拟合风险很小，泛化性能往往优于预剪枝
缺点：后剪枝先生成，后剪枝。自底向上地对树中所有非叶子节点进行逐一考察，训练时间开销比未剪枝的决策树和预剪枝的决策树都要大得多。