1. 决策树基本概念
定义 :一种树形结构分类模型,通过特征判断序列(内部节点)逐步决策,最终到达表示分类结果的叶子节点。
结构组成:
- 内部节点:特征判断条件(如"年龄>30?")
- 分支:判断结果的路径("是"或"否")
- 叶子节点:最终分类结果(如"拒绝贷款")
2. 熵(Entropy)的作用
定义 :信息论中度量随机变量不确定性的指标,计算公式:
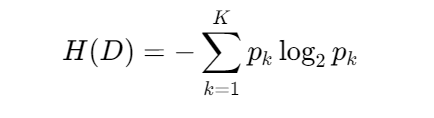
作用:
- 量化数据纯度:熵越小,数据越纯净(如全为同一类别)
- 指导特征选择:ID3/C4.5算法中,通过熵减(信息增益)选择分裂特征
3. CART vs ID3/C4.5 的核心区别
| 维度 | ID3/C4.5 | CART |
|---|---|---|
| 任务支持 | 仅分类 | 分类 + 回归 |
| 树结构 | 多叉树 | 二叉树 |
| 分裂准则 | ID3:信息增益 C4.5:信息增益率 | 分类:基尼指数 回归:平方误差最小化 |
| 缺陷解决 | C4.5修正ID3的多值特征偏好 | 二叉树结构避免多值特征问题 |
4. 节点切分依据
不同算法使用不同分裂准则:
| 算法 | 分裂依据 | 公式/说明 |
|---|---|---|
| ID3 | 信息增益最大 |  |
| C4.5 | 信息增益率最大 | 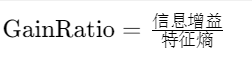 |
| CART | 基尼指数最小(分类) 平方误差最小(回归) | 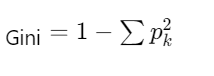 |
5. 剪枝的原因与方法
为什么剪枝:
- 过拟合风险:决策树过度学习训练集噪声
- 泛化需求:提高模型在未知数据的表现
常用剪枝方法:
| 类型 | 操作 | 优缺点 |
|---|---|---|
| 预剪枝 | 树生成中提前停止分裂(如限制深度、叶节点样本数) | ✅ 训练快 ❌ 可能欠拟合 |
| 后剪枝 | 生成完整树后,自底向上替换子树为叶节点(如CCP代价复杂度剪枝) | ✅ 保留有效分支 ❌ 计算开销大 |
总结关键记忆点:
- 熵和基尼指数:衡量数据混乱度,指导特征选择
- 算法差异:CART的二叉树和回归能力是最大特色
- 剪枝本质:模型复杂度和泛化能力的trade-off