【动态规划：背包问题】完全平方数

文章目录

[279. 完全平方数](#279. 完全平方数)
- 解题思路
优化

279. 完全平方数

279. 完全平方数

给你一个整数 n ，返回 和为 n 的完全平方数的最少数量 。

完全平方数 是一个整数，其值等于另一个整数的平方；换句话说，其值等于一个整数自乘的积。例如，1、4、9 和 16 都是完全平方数，而 3 和 11 不是。

示例 1：

复制代码

输入：n = 12
输出：3 
解释：12 = 4 + 4 + 4

示例 2：

复制代码

输入：n = 13
输出：2
解释：13 = 4 + 9

提示：

1 <= n <= 104

解题思路

状态表示

根据 "经验 + 状态表示"，可得 dp[i][j] 表示在前 i 个完全平方数中选，总和正好等于 j，此时的完全平方数的最少数量！

状态转移方程

状态转移方程大体上还是一样的，只不过细节稍微变了点：

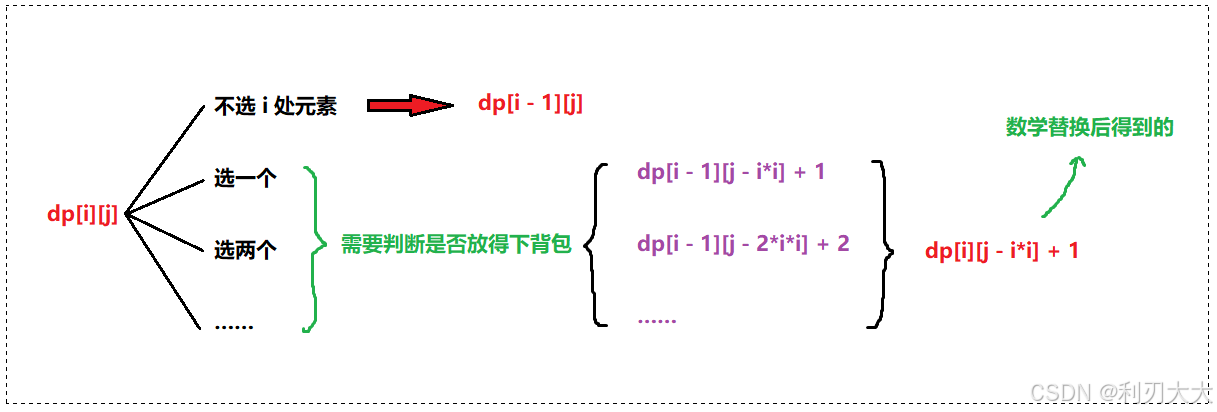
初始化

第一列还是一样不需要初始化，放到填表的时候一起去填！

第一行除了第一个元素之外 ，其它元素其实是不满足状态的，那么为了求最小值的时候不要干扰，我们将其 初始化为 0x3f3f3f3f。

遍历顺序

从上往下，从左往右遍历。

返回值

根据状态表示，我们只需要 返回 dp[m][n] 即可，其中 m 表示根号 n ，因为我们只需要 i 遍历到根号 n 即可，再大了的话其完全平方数就超过 n 了，没意义了！

cpp 复制代码

class Solution {
public:
    int numSquares(int n) {
        // 创建dp表，dp[i][j] 表示在前i个完全平方数中选，总和正好等于j，此时完全平方数的最少数量
        // 并且因为i一定不会走到n那里，因为i*i <= n，所以只需要走到根号n即可
        int m = sqrt(n);
        vector<vector<int>> dp(m + 1, vector<int>(n + 1));

        // 初始化
        for(int j = 1; j <= n; ++j)
            dp[0][j] = 0x3f3f3f3f;

        for(int i = 1; i <= m; ++i)
        {
            for(int j = 1; j <= n; ++j)
            {
                dp[i][j] = dp[i - 1][j];
                if(j >= i*i)
                    dp[i][j] = min(dp[i][j], dp[i][j - i*i] + 1);
            }
        }
        return dp[m][n];
    }
};

优化

所有的「背包问题」，都可以进行空间上的优化。

对于 完全背包 类型的，我们的优化策略是：

删掉第一维

cpp 复制代码

class Solution {
public:
    int numSquares(int n) {
        int m = sqrt(n);
        vector<int> dp(n + 1, 0x3f3f3f3f);

        // 初始化
        dp[0] = 0;

        for(int i = 1; i <= m; ++i)
            for(int j = i*i; j <= n; ++j)
                dp[j] = min(dp[j], dp[j - i*i] + 1);

        return dp[n];
    }
};