LeetCode算法日记 - Day 38: 二叉树的锯齿形层序遍历、二叉树最大宽度

目录

[1. 二叉树的锯齿形层序遍历](#1. 二叉树的锯齿形层序遍历)

[1.1 题目解析](#1.1 题目解析)

[1.2 解法](#1.2 解法)

[1.3 代码实现](#1.3 代码实现)

[2. 二叉树最大宽度](#2. 二叉树最大宽度)

[2.1 题目解析](#2.1 题目解析)

[2.2 解法](#2.2 解法)

[2.3 代码实现](#2.3 代码实现)

---

1. 二叉树的锯齿形层序遍历

https://leetcode.cn/problems/binary-tree-zigzag-level-order-traversal/

给你二叉树的根节点 root ，返回其节点值的 锯齿形层序遍历 。（即先从左往右，再从右往左进行下一层遍历，以此类推，层与层之间交替进行）。

示例 1：

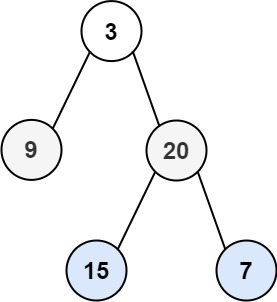
输入：root = [3,9,20,null,null,15,7]
输出：[[3],[20,9],[15,7]]

示例 2：

输入：root = [1]
输出：[[1]]

示例 3：

输入：root = []
输出：[]

提示：

• 树中节点数目在范围 [0, 2000] 内
• -100 <= Node.val <= 100

1.1 题目解析

题目本质： 层序遍历 + 按层"方向交替"的输出（偶数层左→右，奇数层右→左）。核心仍是 BFS 一层一层扫，只是收集每层节点值的顺序要交替。

常规解法： 直接层序遍历，把每层节点值先按正常顺序保存，遇到需要"从右到左"的那层再 reverse 该层结果。

问题分析： 逐层 reverse 的总开销为所有层大小之和，最坏仍是 O(n)，在本题约束（≤2000 节点）下足够。但可以更优雅地避免额外的 reverse：在构建本层列表时就把元素按需要的方向放入头/尾。

思路转折： 要想写法简洁且避免 reverse → 用双端列表保存"当前层结果"：

• 左到右：尾部追加；

• 右到左：头部追加。

  这样层序遍历仍是 O(n)，且实现上更直观。

1.2 解法

算法思想：

BFS 层序队列不变；设置布尔变量 leftToRight 表示本层方向。扫描本层节点时：

• 若 leftToRight == true，将 val 追加到当前层列表尾部；

• 否则，将 val 插入到列表头部。

  层结束后翻转 leftToRight，进入下一层。

**i）**边界：root == null 直接返回空列表。

**ii）**初始化队列 q，将 root 入队；布尔 leftToRight = true。

**iii）**循环直到队列空：获取当前层 size，创建 LinkedList<Integer> cur。

**iiii）**弹出本层 size 个节点：

• 将其值按方向加入 cur 的头/尾；

• 将其左右子节点（若非空）入队。

**iiiii）**将 cur 加入答案列表；leftToRight = !leftToRight。

**iiiiii）**返回答案。

易错点：

• 方向交替的时机：是"每处理完一层"后再翻转，而不是每个节点后翻转。

• 不能对 BFS 入队顺序做方向调整（左右孩子的入队顺序依旧"左先右后"），方向仅影响收集结果的顺序。

• 使用 ArrayDeque 作为队列，不要用 null 元素；当前层大小需预先缓存。

• 若用 ArrayList + Collections.reverse，注意只在需要的层做 reverse，别每层都转。

1.3 代码实现

import java.util.*;

class Solution {
    public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
        List<List<Integer>> ans = new ArrayList<>();
        if (root == null) return ans;

        Deque<TreeNode> q = new ArrayDeque<>();
        q.offer(root);
        boolean leftToRight = true;

        while (!q.isEmpty()) {
            int size = q.size();
            LinkedList<Integer> cur = new LinkedList<>(); // 双端列表，便于头插/尾插

            for (int i = 0; i < size; i++) {
                TreeNode node = q.poll();
                if (leftToRight) cur.addLast(node.val);
                else cur.addFirst(node.val);

                if (node.left != null) q.offer(node.left);
                if (node.right != null) q.offer(node.right);
            }

            ans.add(cur);
            leftToRight = !leftToRight; // 层与层之间交替
        }
        return ans;
    }
}

复杂度分析：

• 时间复杂度 O(n)：每个节点只访问一次，插入头尾 O(1)。

• 空间复杂度 O(n)：队列和结果存储节点值，最宽一层 O(n)。

2. 二叉树最大宽度

https://leetcode.cn/problems/maximum-width-of-binary-tree/

给你一棵二叉树的根节点 root ，返回树的 最大宽度 。

树的 最大宽度 是所有层中最大的 宽度 。

每一层的 宽度 被定义为该层最左和最右的非空节点（即，两个端点）之间的长度。将这个二叉树视作与满二叉树结构相同，两端点间会出现一些延伸到这一层的 null 节点，这些 null 节点也计入长度。

题目数据保证答案将会在 32 位 带符号整数范围内。

示例 1：

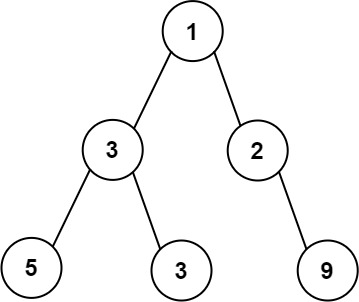
输入：root = [1,3,2,5,3,null,9]
输出：4
解释：最大宽度出现在树的第 3 层，宽度为 4 (5,3,null,9) 。

示例 2：

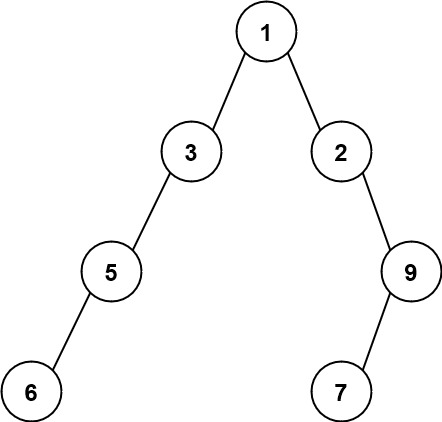
输入：root = [1,3,2,5,null,null,9,6,null,7]
输出：7
解释：最大宽度出现在树的第 4 层，宽度为 7 (6,null,null,null,null,null,7) 。

示例 3：

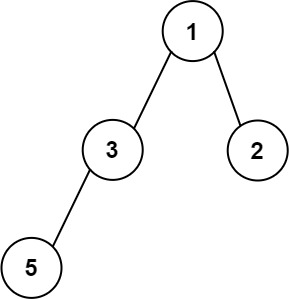
输入：root = [1,3,2,5]
输出：2
解释：最大宽度出现在树的第 2 层，宽度为 2 (3,2) 。

提示：

• 树中节点的数目范围是 [1, 3000]
• -100 <= Node.val <= 100

2.1 题目解析

题目本质：

层序遍历 + 完全二叉树位置编号（index）。同一层的宽度 = 本层最右 index − 本层最左 index + 1。为了把"中间的 null"也计进长度，我们不真去存 null，而是用位置编号来"虚拟补齐"。

常规解法：

BFS 按层扫描，给每个节点一个位置编号：父 i → 左 2i+1、右 2i+2。每层记录头尾的编号差即宽度，取最大值。

问题分析：

直接用 int 编号、一路乘 2 容易溢出（深度大时指数级增长）。另外如果不做处理，编号会越来越大，虽用 long 但也会变得臃肿。

思路转折：

要稳妥且高效 → 两招：

1）用 long 存编号；

2）按层归一化：每层开始时减去该层最小编号 base，让本层从 0 计起。这样可避免指数增长与溢出风险，同时不影响"差值"计算。

2.2 解法

算法思想：

BFS 队列元素为 (node, idx)；层开始取 base = q.peekFirst().idx，本层每个节点用 idx -= base 归一化，记录本层 first 与 last，层宽 last - first + 1，更新答案。孩子入队时使用未归一化前的逻辑（但可以直接在归一化后的 idx 上继续推导：左 idx*2+1，右 idx*2+2，等效）。

**i）**判空返回 0。

**ii）**Deque<P> tmp 入队 (root, 0)；result = 0。

**iii）**while 队列非空：

• 记下 size 与 base = tmp.peekFirst().idx；

• for size 次弹出：

  • 归一化 index = cur.idx - base；

  • 维护本层 first/last；

  • 左右子非空则入队，孩子编号为 index*2+1 / index*2+2；

• 更新 result = max(result, last - first + 1)。

**iiii）**返回 result。

易错点：

• 方向编号选 (2i+1, 2i+2) 或 (2i, 2i+1) 都行，但要全程一致。下面用从 0 开始的 (2i+1, 2i+2)。

• 每层一定要做归一化（减去 base），否则深树时可能溢出或变得非常大。

2.3 代码实现

import java.util.Deque;
import java.util.ArrayDeque;
import java.util.List;
import java.util.ArrayList;

class Solution {
    // 小结构体：存节点和其在完全二叉树中的位置编号
    static class P {
        TreeNode node;
        long idx;
        P(TreeNode n, long i) { node = n; idx = i; }
    }

    public int widthOfBinaryTree(TreeNode root) {
        if (root == null) return 0;

        Deque<P> tmp = new ArrayDeque<>();
        tmp.offer(new P(root, 0L));
        int result = 0;

        while (!tmp.isEmpty()) {
            int size = tmp.size();
            long base = tmp.peekFirst().idx; // 本层最小编号，做归一化
            long first = 0, last = 0;

            for (int i = 0; i < size; i++) {
                P cur = tmp.pollFirst();
                TreeNode node = cur.node;
                long index = cur.idx - base;   // 归一化后，本层从 0 开始

                if (i == 0) first = index;
                if (i == size - 1) last = index;

                // 用归一化后的 index 推孩子的编号，等效且数值更小
                if (node.left != null)  tmp.offer(new P(node.left,  index * 2 + 1));
                if (node.right != null) tmp.offer(new P(node.right, index * 2 + 2));
            }
            result = Math.max(result, (int)(last - first + 1));
        }
        return result;
    }
}

复杂度分析：

• 时间复杂度 O(n)：每个节点入队/出队一次，常数级计算。

• 空间复杂度 O(n)：队列在最宽层持有 O(n) 个节点；额外字段为常数级。