探讨Hyperband 等主要机器学习调优方法的机制和权衡

本篇文章Master Hyperband --- An Efficient Hyperparameter Tuning Method in Machine Learning深入探讨了Hyperband这一高效的超参数调优方法。文章的技术亮点在于其结合了多臂老虎机策略和逐次减半算法，能够在大搜索空间中快速剔除表现不佳的配置，从而节省计算资源。

文章目录

- [1 介绍](#1 介绍)
- [2 什么是 Hyperband](#2 什么是 Hyperband)
- - [2.1 Hyperband 的工作原理](#2.1 Hyperband 的工作原理)
  - [2.1.1 第1步定义预算和淘汰因子](#2.1.1 第1步定义预算和淘汰因子)
  - [2.1.2 第2步遍历各个 Bracket](#2.1.2 第2步遍历各个 Bracket)
  - [2.1.3 第3步运行 Successive Halving Algorithm (SHA)](#2.1.3 第3步运行 Successive Halving Algorithm (SHA))
  - [2.1.4 第4步选出最佳配置](#2.1.4 第4步选出最佳配置)
  - [2.1.5 例子演示 --- 支持向量分类器（SVC）](#2.1.5 例子演示 — 支持向量分类器（SVC）)
- [3 模拟实验](#3 模拟实验)
- - [3.1 创建训练和测试数据集](#3.1 创建训练和测试数据集)
  - [3.2 模型定义 --- LSTM网络](#3.2 模型定义 — LSTM网络)
  - [3.3 搜索空间](#3.3 搜索空间)
  - [3.4 定义验证函数](#3.4 定义验证函数)
  - [3.5 运行 Hyperband](#3.5 运行 Hyperband)
  - [3.6 结果](#3.6 结果)
  - [3.7 与其他调优方法的对比](#3.7 与其他调优方法的对比)
  - [3.8 Bayesian Optimization](#3.8 Bayesian Optimization)
  - [3.9 Random Search](#3.9 Random Search)
  - [3.10 Genetic Algorithms (GA)](#3.10 Genetic Algorithms (GA))
- [4 考虑与总结](#4 考虑与总结)
- - [4.1 提升 Hyperband 性能的建议](#4.1 提升 Hyperband 性能的建议)

1 介绍

Hyperband 是一种强大的机器学习超参数调优方法，利用**successive halving（逐步淘汰）**策略来高效分配资源。

然而，执行 Hyperband 需要对其核心机制和参数进行细致考量，以最大化其优势。

本文将通过调优用于股票价格预测的 LSTM 网络，深入探讨 Hyperband 的核心机制，并与其他主要调优方法进行性能对比：

Bayesian Optimization（贝叶斯优化），
Random Search（随机搜索），以及
Genetic Algorithms（遗传算法）。

2 什么是 Hyperband

Hyperband 是一种高效的超参数调优算法，结合了multi-armed bandit（多臂老虎机）策略和successive halving algorithm（SHA，逐步淘汰算法）。

多臂老虎机问题是概率论中的一个问题，展示了以下基本权衡：

探索（Exploration）： 探索广泛的超参数配置，
利用（Exploitation）： 利用最有前景的配置。

SHA 是一种资源分配策略，它为随机采样的配置分配固定的预算（如训练的epoch数）。

在每个阶段，SHA 评估超参数配置的表现，剔除表现最差的配置，同时将剩余预算重新分配给幸存的配置，称为survivors（幸存者）。

Hyperband 更进一步，通过使用不同的初始预算运行 SHA，以平衡探索和利用。

下面的图表分类展示了主要的超参数调优方法：

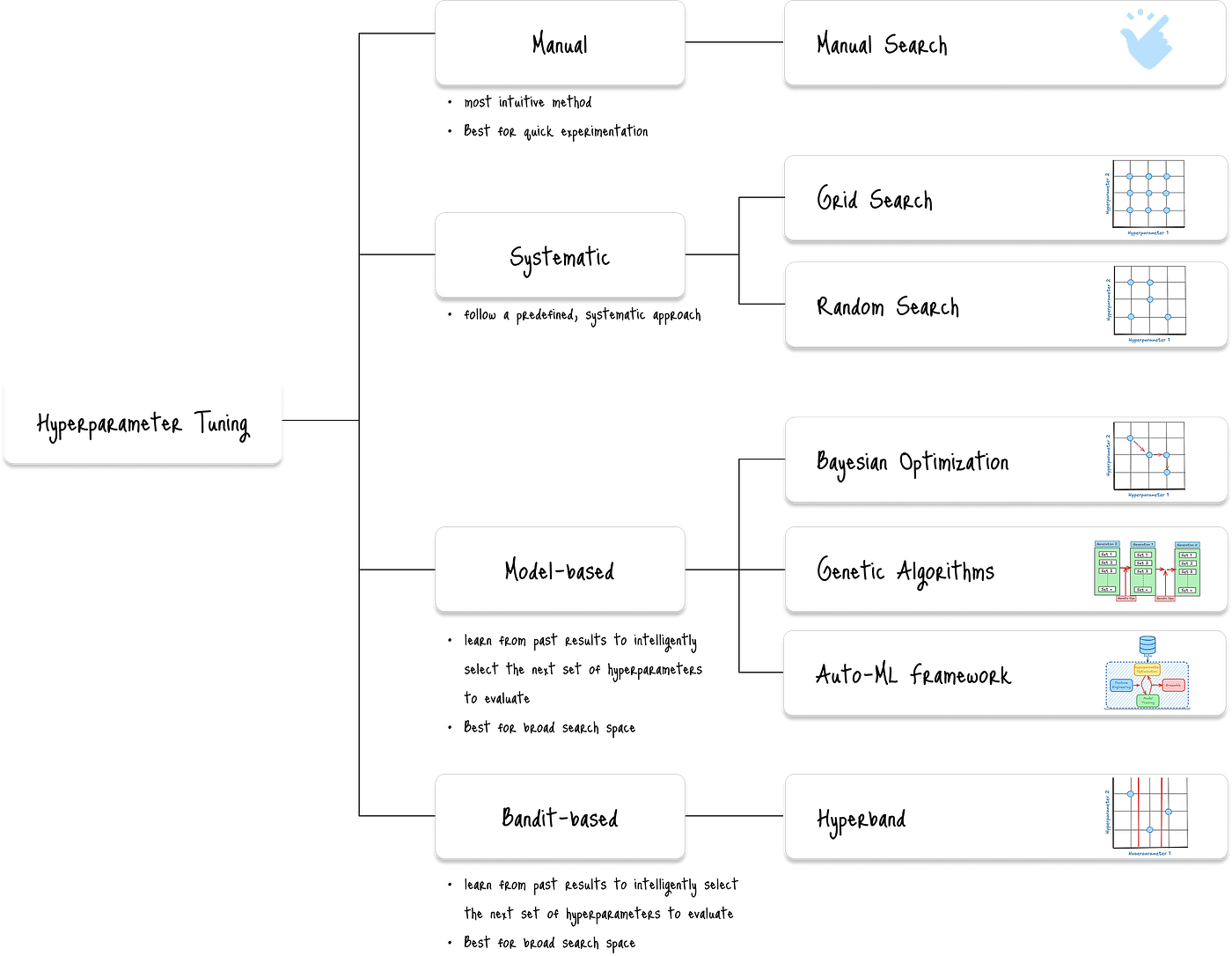
在众多调优方法中，Hyperband 在速度和效率上具有明显优势，尤其适合处理大规模搜索空间。

2.1 Hyperband 的工作原理

下图展示了 Hyperband 如何将更多预算分配给最终胜出者（配置#4），尽管在 Bracket 1 中的初始预算分配是随机的：

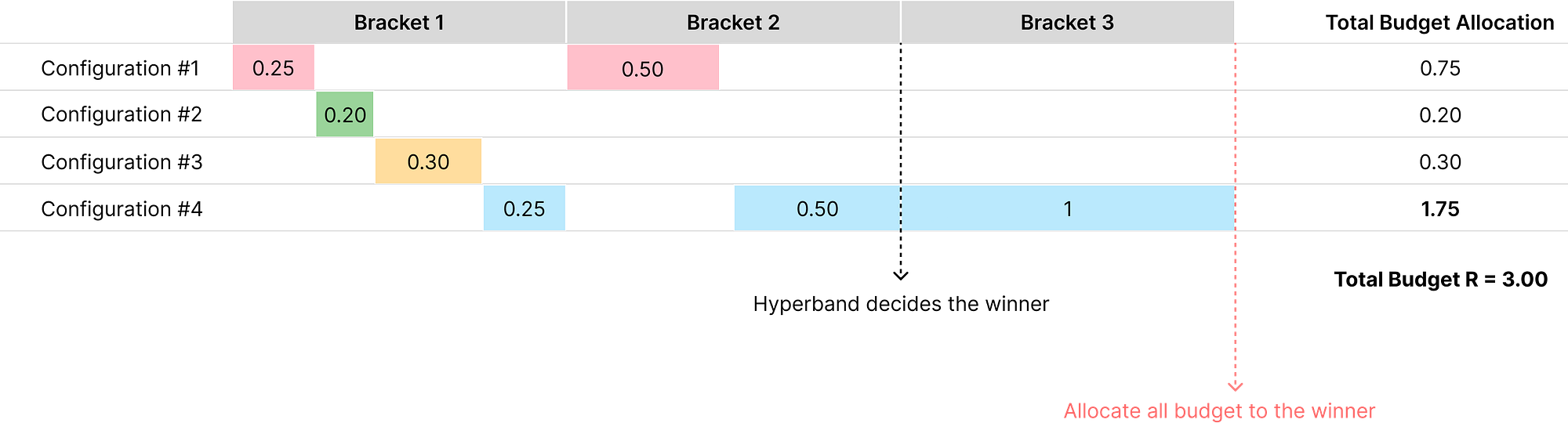
Hyperband 以在Bracket 1中创建大量超参数配置并分配较小预算开始。

随后，随着进入后续的各个 Bracket，配置数量逐步减少，而幸存配置获得更多预算。

在图中的Bracket 2，Hyperband 将更多预算分配给来自 Bracket 1 的幸存者（配置#1和#4）。

最终，在Bracket 3中，将全部预算分配给最终胜出者配置#4。

这种方法有效地探索了广泛的配置，同时快速剔除表现差的配置，实现了探索与利用的平衡。

这一过程可分为四步：

2.1.1 第1步定义预算和淘汰因子

首先定义：

最大资源预算（R）： 单个模型可训练的最大epoch数，
淘汰因子（η）： 预设的因子，用于决定淘汰的激进程度。

常见的淘汰因子值有2、3或4。

每个阶段，超参数配置数量除以η，幸存配置的预算乘以η。

2.1.2 第2步遍历各个 Bracket

算法运行一系列 Bracket，每个 Bracket 是使用不同起始预算的完整 Successive Halving 算法（SHA）运行。

Bracket 数量由最大Bracket索引 s m a x s_{max} smax 决定：

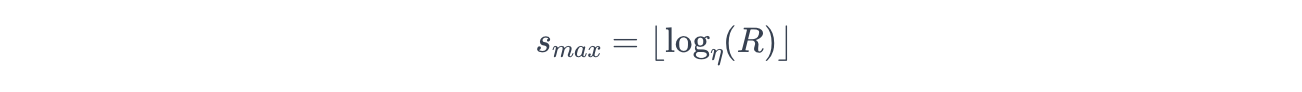
其中：

η η η：淘汰因子，
R R R：最大资源预算。

算法从 s m a x s_{max} smax 迭代到0。

2.1.3 第3步运行 Successive Halving Algorithm (SHA)

对于每个 Bracket s s s，Hyperband 确定开始时的超参数配置数量 n s n_s ns。

Hyperband 有意在预算小的 Bracket 中设置较多配置，预算大的 Bracket 中配置较少。

数学表达式如下：

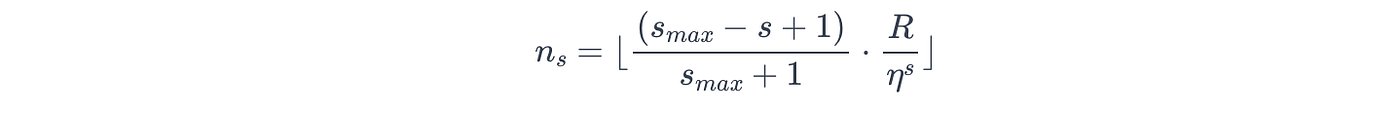
其中：

n s n_s ns：当前Bracket的配置数量，
R R R：最大资源预算，
η η η：淘汰因子，
s m a x s_{max} smax：最大Bracket数，
s s s：当前Bracket索引，范围从 s m a x s_{max} smax 到 0。

Hyperband 还确定每个Bracket的初始预算 r s r_s rs：

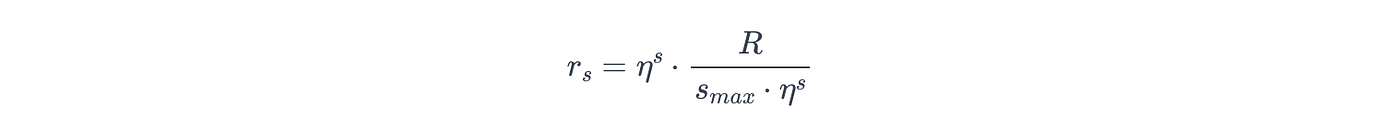
其中：

r s r_s rs：当前Bracket的初始预算，
R R R， η η η， s m a x s_{max} smax 同上。

Hyperband 随机采样 n s n_s ns 个超参数配置，每个训练 r s r_s rs 个 epoch。

然后根据表现选出前 n s / η n_s / η ns/η 个幸存者。

这些幸存者再接受更大预算训练，总训练epoch达到 r s ⋅ η r_s \cdot η rs⋅η。

此过程不断进行，配置数量逐步减半，预算逐步增加，直到只剩一个配置或达到最大预算。

2.1.4 第4步选出最佳配置

所有 Bracket 运行完毕后，选出表现最优的超参数配置作为最终结果。

Hyperband 的效率来自于它能快速剔除表现不佳的配置，释放资源训练更有潜力的配置更长时间。

2.1.5 例子演示 --- 支持向量分类器（SVC）

下面通过调优支持向量分类器（SVC）的正则化参数 C 和核函数系数 gamma，演示 Hyperband 的工作过程。

模型： 支持向量分类器（SVC）

搜索空间：

C: [0.1, 1, 10, 100]
gamma: ['scale', 'auto', 0.1, 1, 10]

第1步定义预算和淘汰因子

设最大预算 R = 81 R=81 R=81，淘汰因子 η = 3 η=3 η=3。

第2步遍历 Bracket

计算最大Bracket索引：

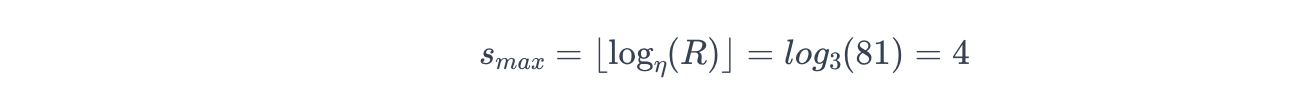
即 Hyperband 将运行 s = 4 , 3 , 2 , 1 , 0 s=4,3,2,1,0 s=4,3,2,1,0 五个 Bracket。

每个 Bracket 的配置数量 n s n_s ns 和初始预算 r s r_s rs 如下：

Bracket 1 ( s = 4 s=4 s=4): n s = 1 n_s=1 ns=1, r s = 9 r_s=9 rs=9
Bracket 2 ( s = 3 s=3 s=3): n s = 3 n_s=3 ns=3, r s = 3 r_s=3 rs=3
Bracket 3 ( s = 2 s=2 s=2): n s = 9 n_s=9 ns=9, r s = 1 r_s=1 rs=1
Bracket 4 ( s = 1 s=1 s=1): n s = 27 n_s=27 ns=27, r s = 1 / 3 r_s=1/3 rs=1/3
Bracket 5 ( s = 0 s=0 s=0): n s = 81 n_s=81 ns=81, r s = 1 / 9 r_s=1/9 rs=1/9

预算 R = 81 R=81 R=81 在这些 Bracket 中分配，以高效寻找最佳配置。

第3步运行 SHA

以 Bracket 3 ( s = 2 s=2 s=2) 为例：

初始运行：

随机采样9个配置，
每个训练1个 epoch，
记录表现，
保留表现最好的3个（ 9 / 3 = 3 9/3=3 9/3=3），其余剔除。

第二轮运行：

这3个幸存者训练3个 epoch（ 1 × 3 = 3 1 \times 3=3 1×3=3），
记录表现，
保留表现最好的1个（ 3 / 3 = 1 3/3=1 3/3=1）。

最终运行：

剩下的单个幸存者训练9个 epoch（ 3 × 3 = 9 3 \times 3=9 3×3=9），
记录表现。

第4步选出最佳

Hyperband 对所有 Bracket 执行上述步骤，最终选出表现最优的配置。

3 模拟实验

接下来，演示 Hyperband 在更复杂模型------LSTM网络上的应用。

模型用于预测选定股票代码 NVDA 的收盘价。

3.1 创建训练和测试数据集

通过 Alpha Vantage API 获取历史日线股价数据。

将数据加载到 Pandas DataFrame 并预处理，划分为训练集和测试集。

训练集用于模型训练和验证，测试集保持独立以防止数据泄露。

python 复制代码

import torch  
import pandas as pd  
from sklearn.model_selection import train_test_split  
from sklearn.preprocessing import StandardScaler, OneHotEncoder  
from sklearn.compose import ColumnTransformer

target_col = 'close'  
y = df.copy()[target_col].shift(-1)   
y = y.iloc[:-1] 

input_cols = [col for col in df.columns if col not in [target_col, 'dt']]   
X = df.copy()[input_cols]  
X = X.iloc[:-1] 

X_train, X_test, y_train, y_test = train_test_split(  
    X, y, test_size=800, shuffle=False, random_state=42  
)

cat_cols = ['year', 'month', 'date']  
num_cols = list(set(input_cols) - set(cat_cols))  
preprocessor = ColumnTransformer(  
    transformers=[  
        ('num', StandardScaler(), num_cols),  
        ('cat', OneHotEncoder(handle_unknown='ignore'), cat_cols)  
    ]  
)  
X_train = preprocessor.fit_transform(X_train)  
X_test = preprocessor.transform(X_test)

X_train = torch.from_numpy(X_train.toarray()).float()  
y_train = torch.from_numpy(y_train.values).float().unsqueeze(1)  
X_test = torch.from_numpy(X_test.toarray()).float()  
y_test = torch.from_numpy(y_test.values).float().unsqueeze(1)

原始数据包含 NVDA 的 6,501 条历史股价记录：

复制代码

<class 'pandas.core.frame.DataFrame'>  
RangeIndex: 6501 entries, 0 to 6500  
Data columns (total 15 columns):  
 0   dt               6501 non-null   datetime64[ns]  
 1   open             6501 non-null   float32         
 2   high             6501 non-null   float32         
 3   low              6501 non-null   float32         
 4   close            6501 non-null   float32         
 5   volume           6501 non-null   int32           
 6   ave_open         6501 non-null   float32         
 7   ave_high         6501 non-null   float32         
 8   ave_low          6501 non-null   float32         
 9   ave_close        6501 non-null   float32         
 10  total_volume     6501 non-null   int32           
 11  30_day_ma_close  6501 non-null   float32         
 12  year             6501 non-null   object          
 13  month            6501 non-null   object          
 14  date             6501 non-null   object          
dtypes: datetime64[ns](1), float32(9), int32(2), object(3)  
memory usage: 482.6+ KB

3.2 模型定义 --- LSTM网络

定义基于 PyTorch 的多对一架构的 LSTMModel 类。

python 复制代码

import torch  
import torch.nn as nn

class LSTMModel(nn.Module):  
    def __init__(self, input_dim, hidden_dim, layer_dim, output_dim, dropout):  
        super(LSTMModel, self).__init__()  
        self.hidden_dim = hidden_dim  
        self.layer_dim = layer_dim  
        self.dropout = dropout  
        self.lstm = nn.LSTM(  
            input_dim, hidden_dim, layer_dim, batch_first=True, dropout=dropout  
        )  
        self.fc = nn.Linear(hidden_dim, output_dim)

    def forward(self, x):  
        h0 = torch.zeros(self.layer_dim, x.size(0), self.hidden_dim).to(x.device)  
        c0 = torch.zeros(self.layer_dim, x.size(0), self.hidden_dim).to(x.device)  
        o_t, _ = self.lstm(x, (h0.detach(), c0.detach()))  
        o_final = self.fc(o_t[:, -1, :])  
        return o_final

3.3 搜索空间

Hyperband 在较大的搜索空间表现更佳。定义如下搜索空间：

python 复制代码

import random

def search_space():  
    return {  
        'lr': 10**random.uniform(-6, -1),  
        'hidden_dim': random.choice([16, 32, 64, 128, 256]),  
        'layer_dim': random.choice([1, 2, 3, 4, 5]),  
        'dropout': random.uniform(0.1, 0.6),  
        'batch_size': random.choice([16, 32, 64, 128, 256])  
    }

3.4 定义验证函数

定义用于时间序列数据的 walk-forward validation（滚动前移验证） 的 train_and_val_wfv 函数：

python 复制代码

def train_and_val_wfv(hyperparams, budget, X, y, train_window, val_window):  
    total_val_loss = 0  
    all_loss_histories = []

    num_folds = (X.size(0) - train_window - val_window) // val_window + 1

    for i in range(num_folds):  
        train_start = i * val_window  
        train_end = train_start + train_window  
        val_start = train_end  
        val_end = val_start + val_window

        if val_end > X.size(0):  
            break

        X_train_fold = X[train_start:train_end]  
        y_train_fold = y[train_start:train_end]  
        X_val_fold = X[val_start:val_end]  
        y_val_fold = y[val_start:val_end]

        fold_val_loss, fold_loss_history = train_and_val(  
            hyperparams=hyperparams,  
            budget=budget,  
            X_train=X_train_fold,  
            y_train=y_train_fold,  
            X_val=X_val_fold,  
            y_val=y_val_fold  
        )  
        total_val_loss += fold_val_loss  
        all_loss_histories.append(fold_loss_history)

    avg_val_loss = total_val_loss / num_folds  
    return avg_val_loss, all_loss_histories

3.5 运行 Hyperband

定义 run_hyperband 函数，接受以下参数：

搜索空间函数 search_space_fn，
验证函数 val_fn，
总预算 R，
淘汰因子 η。

示例中， R = 100 R=100 R=100, η = 3 η=3 η=3，训练和验证窗口分别为3000和500。

python 复制代码

from math import log, floor

def run_hyperband(search_space_fn, val_fn, R, eta):  
    s_max = int(log(R, eta))

    overall_best_config = None  
    overall_best_loss = float('inf')  
    all_loss_histories = []

    for s in range(s_max, -1, -1):  
        n = int(R / eta**s)  
        r = int(R / n)  
        main_logger.info(f'... running bracket s={s}: {n} configurations, initial budget={r} ...')

        configs = [search_space_fn() for _ in range(n)]

        for i in range(s + 1):  
            budget = r * (eta**i)  
            main_logger.info(f'... training {len(configs)} configurations for budget {budget} epochs ...')

            evaluated_results = []  
            for config in configs:  
                loss, loss_history = val_fn(config, budget)  
                evaluated_results.append((config, loss, loss_history))

            all_loss_histories.append((evaluated_results, budget))

            evaluated_results.sort(key=lambda x: x[1])

            if evaluated_results and evaluated_results[0][1] < overall_best_loss:  
                overall_best_loss = evaluated_results[0][1]  
                overall_best_config = evaluated_results[0][0]

            num_to_keep = floor(len(configs) / eta)  
            configs = [result[0] for result in evaluated_results[:num_to_keep]]

            if not configs:  
                break

    return overall_best_config, overall_best_loss, all_loss_histories, s_max

R = 100  
eta = 3

train_window = 3000  
val_window = 500

best_config, best_loss, all_loss_histories, s_max = run_hyperband(  
    search_space_fn=search_space,   
    val_fn=lambda h, b: train_and_val_wfv(h, b, X_train, y_train, train_window=train_window, val_window=val_window),  
    R=R,   
    eta=eta  
)

3.6 结果

最佳超参数配置：

'lr': 0.0001614172022855225
'hidden_dim': 128
'layer_dim': 3
'dropout': 0.5825758700895215
'batch_size': 16

最佳验证损失（均方误差 MSE）：

0.0519

损失历史：

下图中，实线表示训练周期中平均验证损失（MSE）的变化，垂直虚线表示 Hyperband 剪枝不佳模型的时刻：

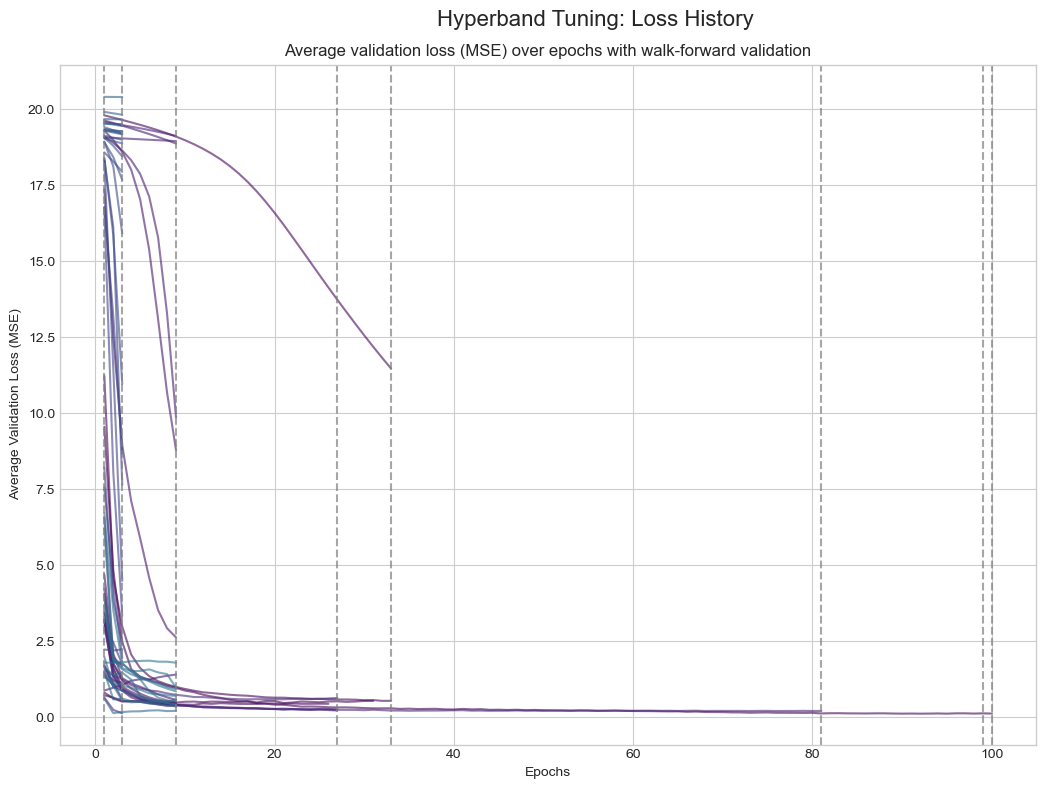
提前停止（大多为紫色）的曲线代表表现不佳被剪枝的模型。

持续训练到100个epoch（大多为青色和蓝色）的曲线代表表现优异的配置，损失迅速下降并稳定在较低值，显示出良好性能。

这种方式能高效快速地剔除表现差的配置，避免长时间训练。

3.7 与其他调优方法的对比

为比较不同方法，进行了20次试验：

Bayesian Optimization（贝叶斯优化），
Random Search（随机搜索），
Genetic Algorithms（遗传算法），

使用相同的搜索空间、模型和训练/验证窗口。

3.8 Bayesian Optimization

贝叶斯优化使用概率模型（如高斯过程）拟合验证误差，选择下一个最优配置进行评估。

最佳超参数配置：

'lr': 0.00016768631941614767
'hidden_dim': 256
'layer_dim': 3
'dropout': 0.3932769195043036
'batch_size': 64

最佳验证损失（MSE）：

0.0428

损失历史：

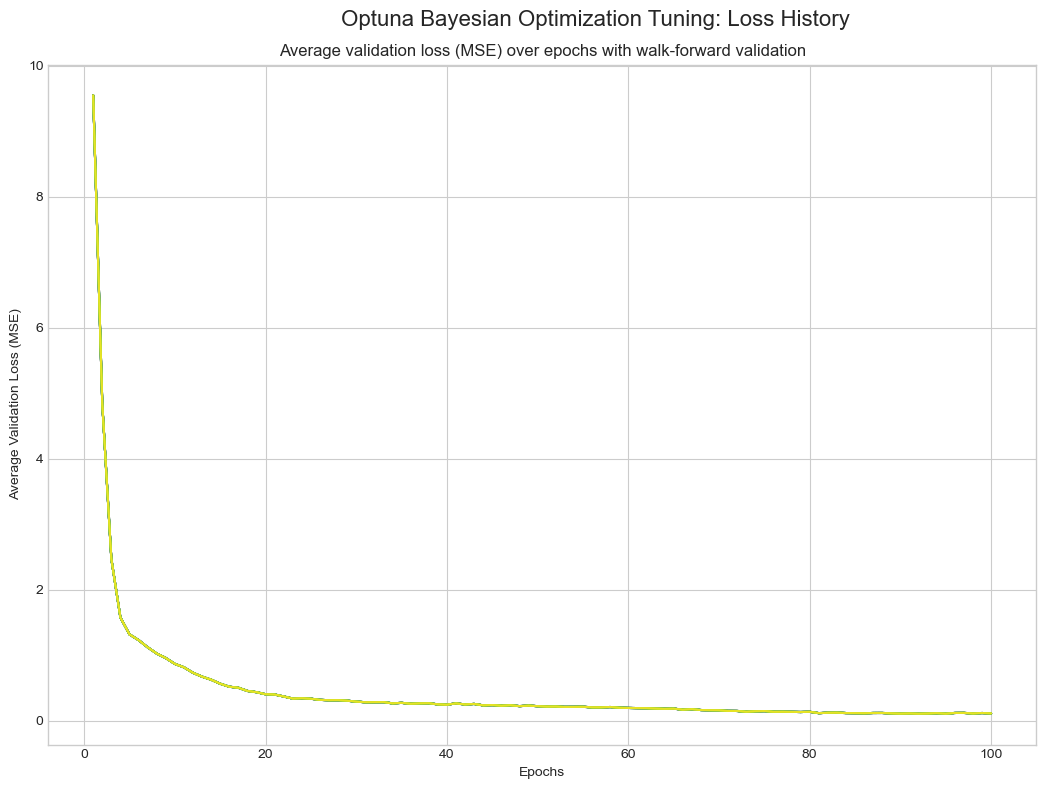
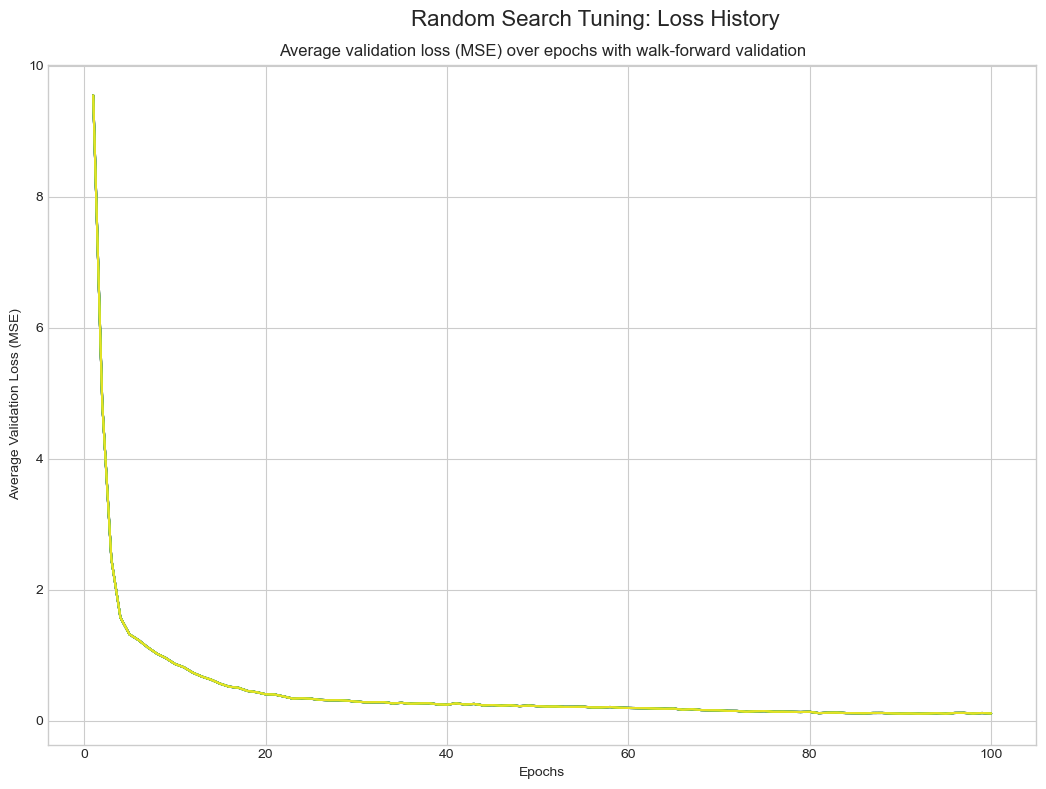
3.9 Random Search

随机搜索从搜索空间随机采样固定数量配置，不利用之前试验结果。

最佳超参数配置：

'lr': 0.0004941205117774383
'hidden_dim': 128
'layer_dim': 2
'dropout': 0.3398469430820351
'batch_size': 64

最佳验证损失（MSE）：

0.03620

损失历史：

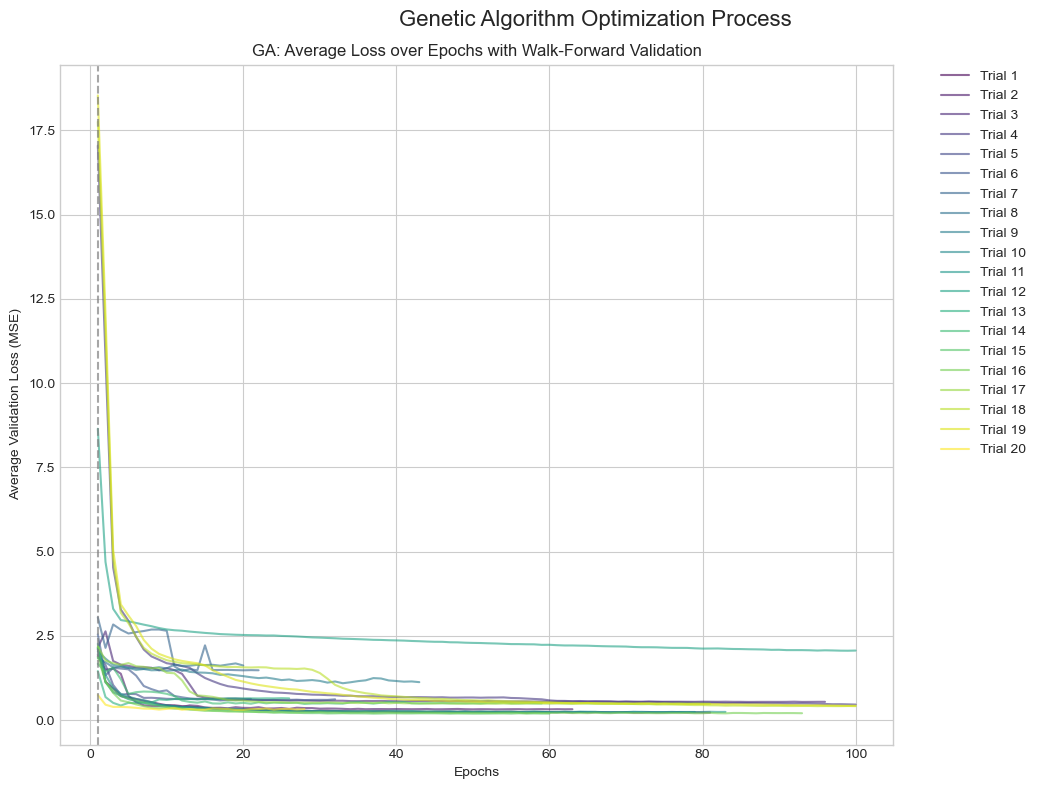
3.10 Genetic Algorithms (GA)

遗传算法受生物进化启发，维护一组配置，通过变异和交叉生成新的潜在更优配置。

最佳超参数配置：

'lr': 0.006441170552290832
'hidden_dim': 128
'layer_dim': 3
'dropout': 0.2052570911345997
'batch_size': 128

最佳验证损失（MSE）：

0.1321

损失历史：

完整源码请见 我的 Github 仓库。

4 考虑与总结

Random Search（0.0362）和 Bayesian Optimization（0.0428）在最终验证损失上略优于 Hyperband（0.0519）。

这体现了效率与全局最优发现能力之间的权衡。

Hyperband 的效率来源于其在训练早期快速剔除表现差的配置。

虽然节省了大量时间，但也存在误删"后期表现优异"配置的风险。

本案例中，Random Search 和 Bayesian Optimization 更成功：

Random Search 允许高性能配置获得完整训练预算，
Bayesian Optimization 通过智能采样更有效地寻找最佳超参数。

4.1 提升 Hyperband 性能的建议

推荐调整 Hyperband 参数并结合其他方法：

调整关键参数

设定较大 R R R（总预算）允许"后期表现优异"模型有机会充分训练，减少误删，
设定较小 η η η（淘汰因子）使淘汰过程更温和，更多配置进入下一轮。

结合贝叶斯优化

BOHB（Bayesian Optimization and HyperBand） 是一种混合方法，使用 Hyperband 的逐步淘汰框架，但用贝叶斯优化替代随机采样。

BOHB 利用贝叶斯优化选择最有潜力的候选配置进入 Hyperband Bracket。

该方法兼具 Hyperband 的快速性和贝叶斯优化的高性能。

探讨Hyperband 等主要机器学习调优方法的机制和权衡

文章目录

1 介绍

2 什么是 Hyperband

2.1 Hyperband 的工作原理

2.1.1 第1步 定义预算和淘汰因子

2.1.2 第2步 遍历各个 Bracket

2.1.3 第3步 运行 Successive Halving Algorithm (SHA)

2.1.4 第4步 选出最佳配置

2.1.5 例子演示 --- 支持向量分类器（SVC）

3 模拟实验

3.1 创建训练和测试数据集

3.2 模型定义 --- LSTM网络

3.3 搜索空间

3.4 定义验证函数

3.5 运行 Hyperband

3.6 结果

3.7 与其他调优方法的对比

3.8 Bayesian Optimization

3.9 Random Search

3.10 Genetic Algorithms (GA)

4 考虑与总结

4.1 提升 Hyperband 性能的建议

2.1.1 第1步定义预算和淘汰因子

2.1.2 第2步遍历各个 Bracket

2.1.3 第3步运行 Successive Halving Algorithm (SHA)

2.1.4 第4步选出最佳配置