OCDM 波形通信感知一体化：从原理到 MATLAB 实现

一、引言

随着 6G 时代的到来，通信感知一体化（Integrated Sensing and Communication, ISAC） 已成为无线通信与雷达探测技术融合发展的关键方向。在这一框架下，通信信号不仅承载数据传输功能，还被赋予了环境感知与目标探测的能力。这种双功能波形设计能够提升频谱利用效率，减少硬件冗余，是未来智能无线网络的重要研究课题。

在众多候选波形中，正交啁啾分复用（Orthogonal Chirp Division Multiplexing, OCDM） 由于其独特的调制方式而受到广泛关注。OCDM 波形由一组正交的啁啾（Chirp）信号构成，啁啾在时域和频域上均有良好的重叠性和正交性。与传统正交频分复用（OFDM）相比，OCDM 具有更强的抗多径衰落性能和鲁棒性，尤其适用于宽带高速场景。

从数学原理来看，OCDM 的生成过程可以通过**离散菲涅尔变换（Discrete Fresnel Transform, DFnT）**及其逆变换实现。设第 m m m 个符号的第 k k k 个子啁啾调制符号为 X m ( k ) X_m(k) Xm(k)，则其离散 OCDM 波形可表示为：

s m ( n ) = e j π / 4 e − j π N n 2 ⋅ IFFT { X m ( k ) e − j π N k 2 } , n = 0 , 1 , ... , N − 1 s_m(n) = e^{j\pi/4} \, e^{-j\frac{\pi}{N}n^2} \cdot \text{IFFT}\Big\{ X_m(k) \, e^{-j\frac{\pi}{N}k^2} \Big\}, \quad n=0,1,\dots,N-1 sm(n)=ejπ/4e−jNπn2⋅IFFT{Xm(k)e−jNπk2},n=0,1,...,N−1

该结构表明，OCDM 波形的生成可以通过 FFT/IFFT 结合相位旋转实现，这使其能够充分复用现有 OFDM 系统的硬件架构，具有良好的实现便利性。

在通信感知一体化系统中，OCDM 波形不仅用于通信信息传输 ，还可通过对接收信号进行频域处理和二维 FFT，实现对目标的距离--速度估计 。具体而言，接收信号经与发射信号的Hadamard 商运算，可以消除通信数据的随机性影响，进而利用离散傅里叶变换提取目标的距离信息与速度信息。这种处理方式在保证通信性能的同时，也显著降低了雷达信号处理的复杂度。

本文将围绕 OCDM 波形的通信感知一体化原理展开，系统介绍其数学建模、通信与感知的联合处理流程，并结合 MATLAB 仿真进行验证，以展示 OCDM 在未来 ISAC 系统中的潜力。

二、OCDM 波形基础

2.1 啁啾信号与正交性

OCDM（Orthogonal Chirp Division Multiplexing）的核心思想是利用一组在 时域与频域上均相互正交的啁啾（Chirp）信号 作为基函数，从而实现多路信息的复用。

第 k k k 个啁啾信号可表示为：

Ψ k ( t ) = e j π N T 2 ( t − k T N ) 2 , k = 0 , 1 , ... , N − 1 \Psi_k(t) = e^{j\pi \frac{N}{T^2}\left(t - \frac{kT}{N}\right)^2}, \quad k=0,1,\dots,N-1 Ψk(t)=ejπT2N(t−NkT)2,k=0,1,...,N−1

其中：

N N N 表示啁啾数（等同于 OCDM 子载波数），
T T T 为 OCDM 信号的符号周期。

这些啁啾信号满足正交性条件：

∫ 0 T Ψ k ( t ) Ψ l ∗ ( t ) d t = { T , k = l 0 , k ≠ l \int_0^T \Psi_k(t) \, \Psi_l^*(t) \, dt = \begin{cases} T, & k=l \\ 0, & k\neq l \end{cases} ∫0TΨk(t)Ψl∗(t)dt={T,0,k=lk=l

由此保证了不同子啁啾在传输时不会互相干扰。

2.2 OCDM 信号的构造

在通信系统中，信息符号 X m ( k ) X_m(k) Xm(k) 被加载到第 m m m 个 OCDM 符号的第 k k k 个啁啾上。离散化后的 OCDM 符号可写为：

s m ( n ) = ∑ k = 0 N − 1 X m ( k ) Ψ k ⁣ ( n T N ) , n = 0 , 1 , ... , N − 1 s_m(n) = \sum_{k=0}^{N-1} X_m(k) \, \Psi_k\!\left(\frac{nT}{N}\right), \quad n=0,1,\dots,N-1 sm(n)=k=0∑N−1Xm(k)Ψk(NnT),n=0,1,...,N−1

进一步推导可得紧凑表达式：

s m ( n ) = e j π / 4 e − j π N n 2 ⋅ IFFT { X m ( k ) e − j π N k 2 } s_m(n) = e^{j\pi/4} \, e^{-j\frac{\pi}{N}n^2} \cdot \text{IFFT}\left\{ X_m(k) \, e^{-j\frac{\pi}{N}k^2} \right\} sm(n)=ejπ/4e−jNπn2⋅IFFT{Xm(k)e−jNπk2}

该式表明 OCDM 波形生成本质上是"加权 IFFT + 相位旋转"，这使其可直接复用 OFDM 的硬件结构，只需增加简单的相位因子调制。

2.3 DFnT 与 IDFnT 的关系

OCDM 调制和解调依赖于 离散菲涅尔变换（Discrete Fresnel Transform, DFnT） 及其逆变换（IDFnT）。

设输入为 X m ( k ) X_m(k) Xm(k)，则 IDFnT 的计算公式为：

s m ( n ) = 1 N e j π / 4 e − j π N n 2 ∑ k = 0 N − 1 X m ( k ) e − j π N k 2 e j 2 π N n k s_m(n) = \frac{1}{\sqrt{N}} \, e^{j\pi/4} \, e^{-j\frac{\pi}{N}n^2} \sum_{k=0}^{N-1} X_m(k) \, e^{-j\frac{\pi}{N}k^2} \, e^{j\frac{2\pi}{N}nk} sm(n)=N 1ejπ/4e−jNπn2k=0∑N−1Xm(k)e−jNπk2ejN2πnk

接收端则通过 DFnT 完成逆过程：

X m ( k ) = 1 N e − j π / 4 e j π N k 2 ∑ n = 0 N − 1 s m ( n ) e j π N n 2 e − j 2 π N n k X_m(k) = \frac{1}{\sqrt{N}} \, e^{-j\pi/4} \, e^{j\frac{\pi}{N}k^2} \sum_{n=0}^{N-1} s_m(n) \, e^{j\frac{\pi}{N}n^2} \, e^{-j\frac{2\pi}{N}nk} Xm(k)=N 1e−jπ/4ejNπk2n=0∑N−1sm(n)ejNπn2e−jN2πnk

由此可见，OCDM 的调制与解调都可以通过 FFT/IFFT + 相位旋转来实现，复杂度与 OFDM 基本相同，但啁啾信号的引入带来了更好的多径抗性。

2.4 OCDM 与 OFDM 的对比

OFDM ：采用复指数基函数 e j 2 π k n / N e^{j2\pi kn/N} ej2πkn/N，仅在频域上正交。
OCDM ：采用啁啾基函数 Ψ k ( n ) \Psi_k(n) Ψk(n)，在时域和频域均正交。

因此 OCDM 在频率选择性衰落信道中表现出更好的抗干扰性能，非常适合应用于通信感知一体化场景。

三、通信系统原理

3.1 发射端流程

OCDM 通信系统的发射端与传统 OFDM 系统类似，但在调制环节采用 逆离散菲涅尔变换（IDFnT） 代替 IFFT。整体流程如下：

比特加载 ：输入比特流按 log ⁡ 2 M \log_2 M log2M 位分组，经 M M M 阶 QAM 映射为符号 X m ( k ) X_m(k) Xm(k)。
OCDM 调制 ：每个符号块 X m ( k ) X_m(k) Xm(k) 经过 IDFnT 变换得到时域 OCDM 信号 s m ( n ) s_m(n) sm(n)。
循环前缀（GI/CP） ：为抵消多径引入的符号间干扰 (ISI)，在每个 OCDM 块前加上长度为 G G G 的循环前缀。
发射信号：经 DAC 和射频上变频后由天线发射。

数学上，第 m m m 个 OCDM 符号块在时域的形式为：

3.2 信道模型

设发射信号经过 多径衰落信道，其冲激响应为：

h ( τ ) = ∑ l = 0 L − 1 α l δ ( τ − τ l ) h(\tau) = \sum_{l=0}^{L-1} \alpha_l \, \delta(\tau - \tau_l) h(τ)=l=0∑L−1αlδ(τ−τl)

其中：

α l \alpha_l αl 为第 l l l 条径的复增益，
τ l \tau_l τl 为相应时延。

则接收信号可表示为：

r m ( n ) = ∑ l = 0 L − 1 α l s m ( n − τ l ) + w ( n ) r_m(n) = \sum_{l=0}^{L-1} \alpha_l \, s_m(n - \tau_l) + w(n) rm(n)=l=0∑L−1αlsm(n−τl)+w(n)

其中 w ( n ) w(n) w(n) 为加性高斯白噪声 (AWGN)。

3.3 接收端流程

接收端的主要步骤为：

去除循环前缀 ，得到长度为 N N N 的有效符号。
OCDM 解调 ：通过 离散菲涅尔变换（DFnT） 实现：
Y m ( k ) = DFnT { r m ( n ) } Y_m(k) = \text{DFnT}\{r_m(n)\} Ym(k)=DFnT{rm(n)}
均衡与判决 ：根据信道估计对 Y m ( k ) Y_m(k) Ym(k) 进行均衡，得到估计符号 X ^ m ( k ) \hat{X}_m(k) X^m(k)。
QAM 解映射 ：将 X ^ m ( k ) \hat{X}_m(k) X^m(k) 转换为比特流，完成解调。

3.4 性能度量

OCDM 通信性能主要通过以下指标评估：

误码率 (BER)
BER = 1 N b ∑ i = 1 N b I ( b i ≠ b ^ i ) \text{BER} = \frac{1}{N_b} \sum_{i=1}^{N_b} \mathbb{I}(b_i \neq \hat{b}_i) BER=Nb1i=1∑NbI(bi=b^i)

其中 N b N_b Nb 为比特总数， I ( ⋅ ) \mathbb{I}(\cdot) I(⋅) 为指示函数。
误差向量幅度 (EVM)
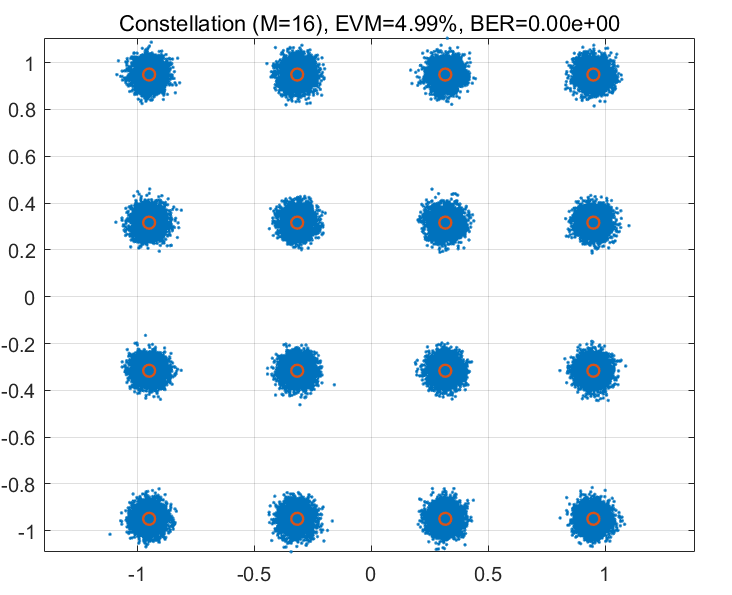
EVM rms = E [ ∣ X m ( k ) − X ^ m ( k ) ∣ 2 ] E [ ∣ X m ( k ) ∣ 2 ] × 100 % \text{EVM}_{\text{rms}} = \sqrt{\frac{\mathbb{E}[|X_m(k) - \hat{X}_m(k)|^2]}{\mathbb{E}[|X_m(k)|^2]}} \times 100\% EVMrms=E[∣Xm(k)∣2]E[∣Xm(k)−X^m(k)∣2] ×100%

EVM 反映星座点的畸变程度，而 BER 则是最终通信质量的衡量指标。

3.5 OCDM 与 OFDM 的对比

基函数不同 ：OFDM 基于复指数函数 e j 2 π k n / N e^{j2\pi kn/N} ej2πkn/N，而 OCDM 基于正交啁啾函数 Ψ k ( n ) \Psi_k(n) Ψk(n)。
调制方式不同：OFDM 使用 IFFT/FFT，OCDM 使用 IDFnT/DFnT。
抗多径性能：由于啁啾信号在时频双域具有扩展性，OCDM 在多径环境下往往优于 OFDM。

因此，在 6G 通信感知一体化 的场景下，OCDM 既能保证通信可靠性，又能兼顾雷达感知处理。

四、感知系统原理

在通信感知一体化（ISAC）系统中，OCDM 波形不仅可以承载通信数据，还能够同时用于目标探测。其感知处理的基本思路是：通过接收端信号与发射端信号的联合处理，消除通信符号的随机性影响，从而提取目标的距离与速度信息。

4.1 单目标回波模型

假设发射端发送 OCDM 信号 s m ( n ) s_m(n) sm(n)，当系统存在单个目标时，接收端的离散回波模型可表示为：

r m ( n ) = A ⋅ s m ⁣ ( n − τ N T ) ⋅ e j 2 π f d m T r_m(n) = A \cdot s_m\!\left(n - \tau \frac{N}{T}\right) \cdot e^{j2\pi f_d mT} rm(n)=A⋅sm(n−τTN)⋅ej2πfdmT

其中：

A A A 为信道增益（包含目标反射系数和路径损耗），
τ \tau τ 为时延，对应目标距离 R = c 0 τ 2 R=\frac{c_0 \tau}{2} R=2c0τ，
f d = 2 v f c c 0 f_d = \frac{2 v f_c}{c_0} fd=c02vfc 为多普勒频移，对应相对速度 v v v，
T T T 为 OCDM 符号周期， N N N 为子啁啾数。

该公式表明，目标回波相较于发射信号产生了 时延（距离信息） 与 相位调制（速度信息）。

4.2 频域表达与 Hadamard 商

对接收信号做傅里叶变换，得到频域表示：

F r x , m ( k ) = A ⋅ F t x , m ( k ) ⋅ e − j 2 π N 2 R c 0 T k ⋅ e j 2 π 2 f c v c 0 m T F_{rx,m}(k) = A \cdot F_{tx,m}(k) \cdot e^{-j\frac{2\pi}{N}\frac{2R}{c_0 T}k} \cdot e^{j2\pi \frac{2 f_c v}{c_0} mT} Frx,m(k)=A⋅Ftx,m(k)⋅e−jN2πc0T2Rk⋅ej2πc02fcvmT

其中：

F t x , m ( k ) F_{tx,m}(k) Ftx,m(k) 为发射信号的频域表达，
指数项中 k k k 与 m m m 分别体现了距离与速度的调制效应。

为了消除通信符号的影响，可以构造 Hadamard 商：

Z ( k , m ) = F r x , m ( k ) F t x , m ( k ) = A ⋅ g R ( k ) ⋅ g v ( m ) Z(k,m) = \frac{F_{rx,m}(k)}{F_{tx,m}(k)} = A \cdot g_R(k) \cdot g_v(m) Z(k,m)=Ftx,m(k)Frx,m(k)=A⋅gR(k)⋅gv(m)

其中：

距离因子
g R ( k ) = e − j 2 π 2 R c 0 T k N g_R(k) = e^{-j2\pi \frac{2R}{c_0 T}\frac{k}{N}} gR(k)=e−j2πc0T2RNk
速度因子
g v ( m ) = e j 2 π 2 f c v c 0 m T g_v(m) = e^{j2\pi \frac{2 f_c v}{c_0} mT} gv(m)=ej2πc02fcvmT

此时， Z ( k , m ) Z(k,m) Z(k,m) 中已不含调制符号信息，仅包含目标的距离与速度特征。

4.3 距离--速度二维估计

在去除通信符号干扰后，可通过二维变换提取目标参数：

距离估计 ：对 k k k 维（频域维度）进行 IFFT，得到距离维谱：
R ( n , m ) = IFFT k { Z ( k , m ) } R(n,m) = \text{IFFT}_k \{ Z(k,m) \} R(n,m)=IFFTk{Z(k,m)}

峰值对应的采样点 n n n 与目标距离 R R R 近似关系为：
R ≈ n c 0 2 B R \approx \frac{n c_0}{2B} R≈2Bnc0
速度估计 ：对 m m m 维（慢时域符号维度）进行 FFT，得到速度维谱：
R D ( n , f ) = FFT m { R ( n , m ) } RD(n,f) = \text{FFT}_m \{ R(n,m) \} RD(n,f)=FFTm{R(n,m)}

峰值对应的频率 f d f_d fd 与速度 v v v 的关系为：
v ≈ λ 2 f d v \approx \frac{\lambda}{2} f_d v≈2λfd

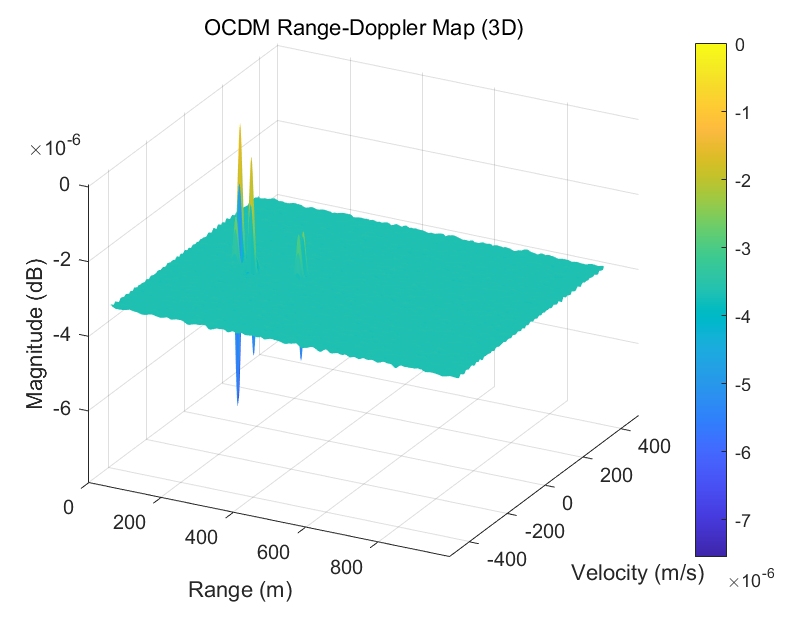
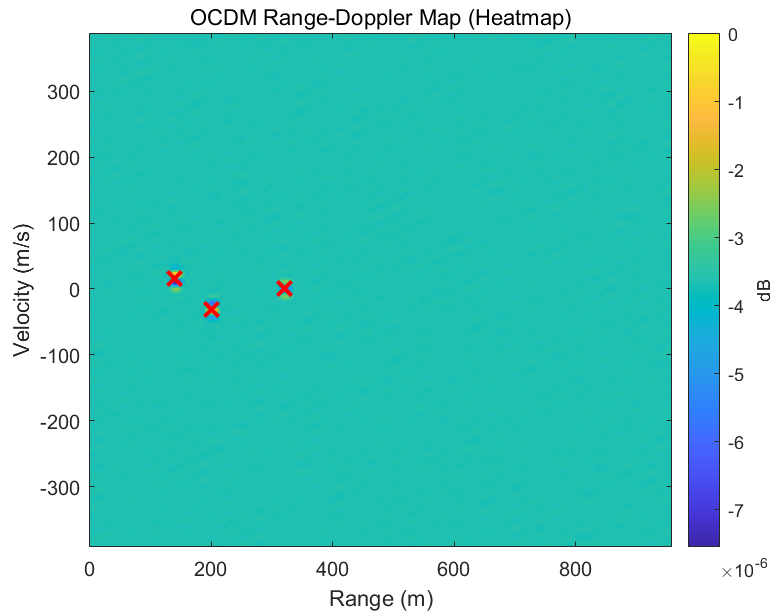
最终即可得到目标的 距离--速度二维谱（Range--Doppler Map）。

4.4 多目标场景扩展

当存在 P P P 个目标时，接收信号为各个目标回波的叠加：

r m ( n ) = ∑ p = 1 P A p s m ⁣ ( n − τ p N T ) e j 2 π f d , p m T r_m(n) = \sum_{p=1}^P A_p \, s_m\!\left(n - \tau_p \frac{N}{T}\right) e^{j2\pi f_{d,p} mT} rm(n)=p=1∑PApsm(n−τpTN)ej2πfd,pmT

对应的 Hadamard 商为：

Z ( k , m ) = ∑ p = 1 P A p g R , p ( k ) g v , p ( m ) Z(k,m) = \sum_{p=1}^P A_p \, g_{R,p}(k) \, g_{v,p}(m) Z(k,m)=p=1∑PApgR,p(k)gv,p(m)

二维 FFT 后，在 Range--Doppler 平面上会出现多个峰值，每个峰值对应一个目标的 距离--速度坐标。

4.5 小结

OCDM 感知系统的核心在于：

回波模型：信号在距离维产生时延，在速度维产生相位调制；
符号消除：通过 Hadamard 商去除通信符号影响；
参数估计：二维 FFT 分别提取目标的距离与速度。

这种方法与传统雷达的匹配滤波相比，复杂度更低，且天然兼容通信功能，非常适合 6G 场景下的通信感知一体化应用。

五、通信感知一体化框架

OCDM 波形的一个核心优势在于，其调制解调过程与感知处理过程可以共享同一物理信号 s m ( n ) s_m(n) sm(n)，从而实现真正意义上的 通信感知一体化（ISAC）。在这一框架下，通信与感知既相互独立又高度协同。

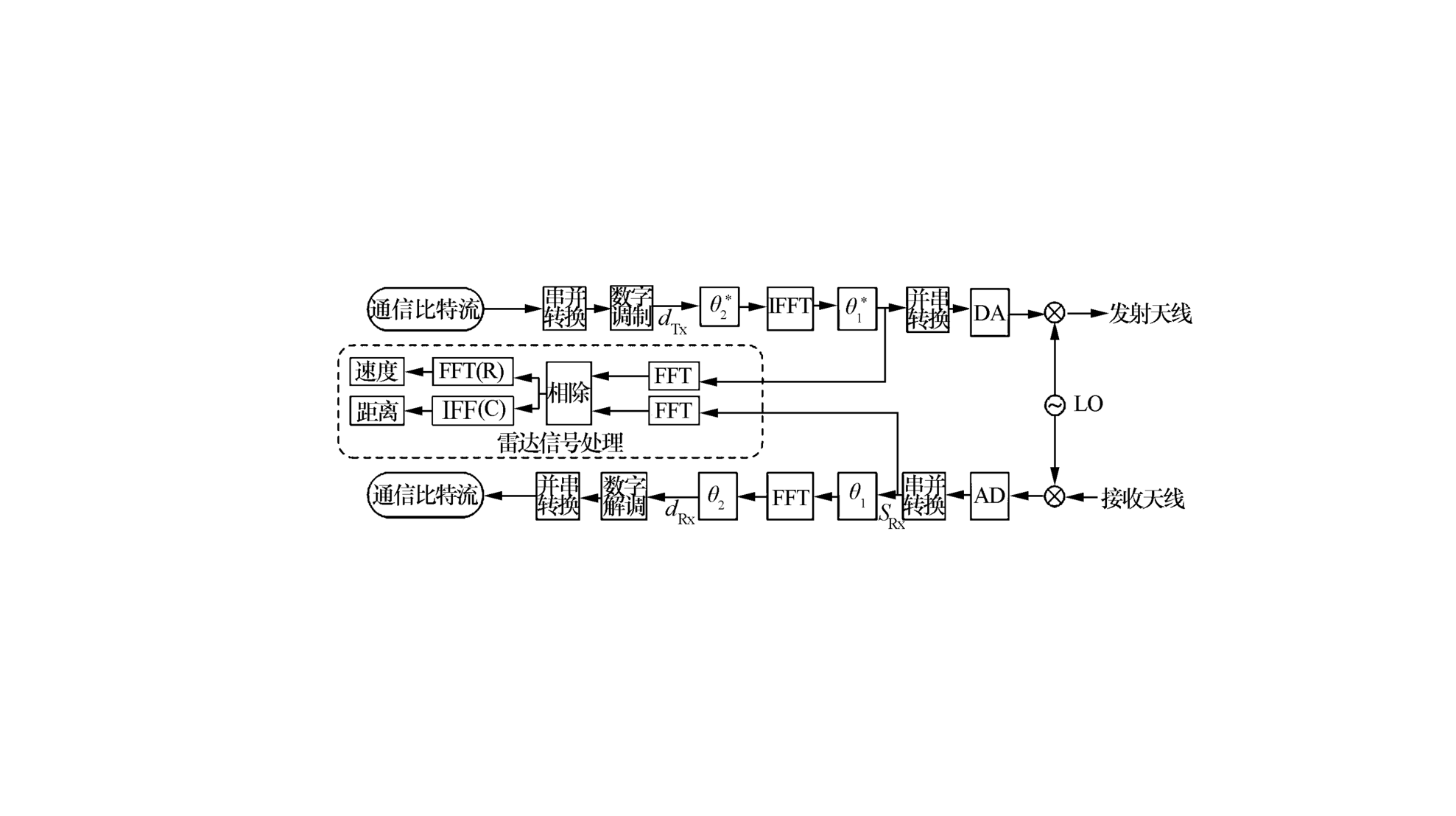
5.1 发射端统一建模

在发射端，信息比特经过 QAM 映射得到符号 X m ( k ) X_m(k) Xm(k)，再通过 逆离散菲涅尔变换（IDFnT） 得到时域 OCDM 信号：

发射端信号经过 DAC 和上变频后由天线发射，用于同时执行 通信传输 与 雷达感知。

5.2 接收端的双支路处理

在接收端，信号经过下变频和采样后，被分为 通信支路 与 感知支路：

通信支路
- 去除循环前缀 (CP)
- 通过 DFnT 解调：
  Y m ( k ) = DFnT { r m ( n ) } Y_m(k) = \text{DFnT}\{r_m(n)\} Ym(k)=DFnT{rm(n)}
- 均衡与判决，得到估计符号 X ^ m ( k ) \hat{X}_m(k) X^m(k)
- QAM 解映射恢复比特流
感知支路
- 将接收信号与发射信号在频域做 Hadamard 商 ：
  Z ( k , m ) = F r x , m ( k ) F t x , m ( k ) Z(k,m) = \frac{F_{rx,m}(k)}{F_{tx,m}(k)} Z(k,m)=Ftx,m(k)Frx,m(k)
- 对 k k k 维进行 IFFT，得到目标的距离信息
- 对 m m m 维进行 FFT，得到目标的速度信息
- 形成 距离--速度二维谱（Range--Doppler Map）

5.3 通信与感知的统一性

在该一体化框架下，通信与感知的数学模型可以统一表示为：

通信目标：最小化误码率 (BER)、提升调制解调精度 (EVM)
感知目标 ：在 Range--Doppler 平面上检测并估计目标参数 ( R , v ) (R,v) (R,v)

两者均基于同一信号 s m ( n ) s_m(n) sm(n)，其变换关系总结如下表：

模块	数学操作	提取信息
IDFnT	X m ( k ) → s m ( n ) X_m(k) \to s_m(n) Xm(k)→sm(n)	波形生成
DFnT	r m ( n ) → Y m ( k ) r_m(n) \to Y_m(k) rm(n)→Ym(k)	通信符号检测
Hadamard 商	F r x ( k , m ) / F t x ( k , m ) F_{rx}(k,m)/F_{tx}(k,m) Frx(k,m)/Ftx(k,m)	去除通信符号影响
IFFT (列)	Z ( k , m ) → R ( n , m ) Z(k,m) \to R(n,m) Z(k,m)→R(n,m)	目标距离
FFT (行)	R ( n , m ) → R D ( n , f ) R(n,m) \to RD(n,f) R(n,m)→RD(n,f)	目标速度

5.4 小结

OCDM 波形的一体化框架表明：

同一套调制解调结构可同时支持通信与感知；
FFT/IFFT 与相位旋转是整个系统的核心算子；
通过 Hadamard 商 将通信与感知解耦，实现双功能共存。

因此，OCDM 为未来 6G 场景中的 ISAC 系统提供了一个 低复杂度、强鲁棒性 的解决方案。

六、MATLAB 验证

为了验证 OCDM 波形在通信感知一体化中的性能，可以采用 MATLAB 搭建仿真平台。下面给出简化的伪代码流程，分别对应 通信链路 与 感知链路。

6.1 通信链路验证

matlab 复制代码

% 参数设置
设定 QAM 阶数 M, OCDM 子啁啾数 N, 符号块数 NumBlocks, Eb/N0 等参数

% 发射端
生成随机比特流 → QAM 调制
符号矩阵 reshape → IDFnT 变换得到时域 OCDM 信号
加入循环前缀 (CP)

% 信道
通过 AWGN 或多径信道传输

% 接收端
去除循环前缀 → DFnT 变换恢复符号
QAM 解调 → 计算 BER 和 EVM

% 输出结果
打印 BER, EVM，绘制星座图

6.2 感知链路验证

matlab 复制代码

% 参数设置
设定载波频率 fc, 信号带宽 B, 子啁啾数 N, 符号数 M
设定目标距离 R_p, 速度 v_p, 反射系数 alpha_p

% 发射端
QAM 符号矩阵 → IDFnT → OCDM 发射信号

% 回波建模
对每个目标叠加时延 (R) 与多普勒 (v)
得到接收信号矩阵 RxOCDM

% 通信符号消除
Ftx = fft(TxOCDM) , Frx = fft(RxOCDM)
Hadamard 商: H_est = Frx ./ Ftx

% 距离--速度估计
对列做 IFFT → 得到距离维
对行做 FFT → 得到速度维
生成 Range--Doppler Map

% 可视化
绘制三维曲面图
绘制二维热力图并标注真实目标位置

6.3 小结

通过上述 MATLAB 仿真流程，可以同时验证：

通信性能：误码率 (BER)、误差向量幅度 (EVM)、星座图分布
感知性能：目标的距离--速度估计结果，Range--Doppler 图与理论值对比

结果表明，OCDM 波形能够在保证通信可靠性的同时，实现对多目标的有效探测，体现了通信感知一体化的优势。

七、总结

本文围绕 OCDM 波形的通信感知一体化原理 展开，系统介绍了从基础理论到系统框架再到 MATLAB 验证的全过程。主要结论如下：

OCDM 波形的本质

OCDM 基于正交啁啾信号，通过 离散菲涅尔变换（DFnT/IDFnT） 实现调制与解调。其数学结构可以看作是 OFDM 的扩展形式，仅需在 FFT/IFFT 前后引入相位因子，即可完成高效实现。
通信系统性能

在通信链路中，OCDM 通过 QAM 调制与 IDFnT 变换实现信息传输，具备良好的 误码率 (BER) 与 误差向量幅度 (EVM) 表现，且在多径信道中展现出比 OFDM 更强的鲁棒性。
感知系统性能

在感知链路中，接收信号经与发射信号的 Hadamard 商 处理，能够有效去除通信符号随机性影响。随后通过二维 FFT 得到 距离--速度谱 (Range--Doppler Map)，实现了目标的距离与速度联合估计。
一体化框架优势

通信与感知基于同一 OCDM 信号实现，共享调制解调模块 ，不仅降低了硬件复杂度，还提升了频谱利用率，是典型的 ISAC 波形候选方案。

因此，OCDM 不仅是一种新型调制方式，更是面向 6G 时代 通信与感知深度融合 的重要技术支撑。

八、完整代码

本文的完整代码在我的github上。开源链接为：hjHe-ee/OCDM-ISAC