【漫话机器学习系列】003.Agglomerative聚类

拟合度概念及意义

Agglomerative 聚类（层次聚类中的自底向上方法）

Agglomerative 聚类是一种层次聚类（Hierarchical Clustering）算法，采用自底向上的策略，将每个数据点看作一个单独的簇，然后逐步将相近的簇合并，直到满足停止条件。

1. 算法简介

基本思想

每个样本初始为一个独立的簇。
根据一定的相似性度量（如欧几里得距离、余弦相似度等），迭代地合并最相似的簇。
最终形成一个簇或层次化的聚类结果（以树状图表示）。

2. 算法步骤

初始化：
- 每个数据点作为一个单独的簇。
计算距离矩阵：
- 计算所有簇之间的相似度（距离），存储在矩阵中。
合并最近的簇：
- 找到距离最近的两个簇，合并成一个新簇。
更新距离矩阵：
- 根据新的簇重新计算与其他簇的距离。
重复步骤 3 和 4：
- 直到所有点合并为一个簇，或满足停止条件。

停止条件

指定的簇数量 k 达到。
聚类距离超过设定阈值。

3. 距离计算方法

聚类中簇之间的距离可以通过以下方法定义：

(1) 单链接（Single Linkage）

<math xmlns="http://www.w3.org/1998/Math/MathML"> d ( C i , C j ) = min ⁡ { d ( x p , x q ) : x p ∈ C i , x q ∈ C j } d(C_i, C_j) = \min\{d(x_p, x_q) : x_p \in C_i, x_q \in C_j\} </math>d(Ci,Cj)=min{d(xp,xq):xp∈Ci,xq∈Cj}

两簇中最近的点之间的距离。
优点：适合长条形状的簇。
缺点：对噪声和异常值敏感。

(2) 全链接（Complete Linkage）

<math xmlns="http://www.w3.org/1998/Math/MathML"> d ( C i , C j ) = max ⁡ { d ( x p , x q ) : x p ∈ C i , x q ∈ C j } d(C_i, C_j) = \max\{d(x_p, x_q) : x_p \in C_i, x_q \in C_j\} </math>d(Ci,Cj)=max{d(xp,xq):xp∈Ci,xq∈Cj}

两簇中最远的点之间的距离。
优点：生成紧密的簇。
缺点：可能导致小簇。

(3) 平均链接（Average Linkage）

<math xmlns="http://www.w3.org/1998/Math/MathML"> d ( x p , x q ) d ( C i , C j ) = 1 ∣ C i ∣ ⋅ ∣ C j ∣ ∑ x p ∈ C i ∑ x q ∈ C j d ( x p , x q ) d(xp,xq)d(C_i, C_j) = \frac{1}{|C_i| \cdot |C_j|} \sum_{x_p \in C_i} \sum_{x_q \in C_j} d(x_p, x_q) </math>d(xp,xq)d(Ci,Cj)=∣Ci∣⋅∣Cj∣1∑xp∈Ci∑xq∈Cjd(xp,xq)

簇中所有点对之间的平均距离。
优点：平衡单链接和全链接的极端情况。

(4) 中心距离（Centroid Linkage）

<math xmlns="http://www.w3.org/1998/Math/MathML"> d ( C i , C j ) = d ( μ i , μ j ) d(C_i, C_j) = d(\mu_i, \mu_j) </math>d(Ci,Cj)=d(μi,μj)

两簇质心（均值）之间的距离。

(5) Ward's 方法

<math xmlns="http://www.w3.org/1998/Math/MathML"> d ( C i , C j ) = Δ S S E = S S E n e w − ( S S E i + S S E j ) d(C_i, C_j) = \Delta SSE = SSE_{new} - (SSE_i + SSE_j) </math>d(Ci,Cj)=ΔSSE=SSEnew−(SSEi+SSEj)

合并后簇内误差平方和的增量。
优点：通常生成更加平衡的聚类结果。

4. 特点

优点

无需预设簇数 k：通过树状图可以分析多种聚类结果。
适用于任意形状簇：适合非凸形状的分布。
层次结构：提供数据的分层信息，有助于理解数据的内在结构。

缺点

计算复杂度高 ：距离矩阵的计算和更新代价较大，复杂度为 <math xmlns="http://www.w3.org/1998/Math/MathML"> O ( n 3 ) O(n^3) </math>O(n3)。
对噪声敏感：异常值可能显著影响结果。
不适用于大规模数据集：计算量随样本数量呈平方增长。

5. Python 实现

使用 `scikit-learn` 的 Agglomerative Clustering

ini 复制代码

from sklearn.cluster import AgglomerativeClustering
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt

# 生成数据
X, _ = make_blobs(n_samples=300, centers=4, cluster_std=0.6, random_state=42)

# 进行层次聚类
clustering = AgglomerativeClustering(n_clusters=4, linkage='ward')
labels = clustering.fit_predict(X)

# 可视化结果
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis', s=50)
plt.title('Agglomerative Clustering')
plt.show()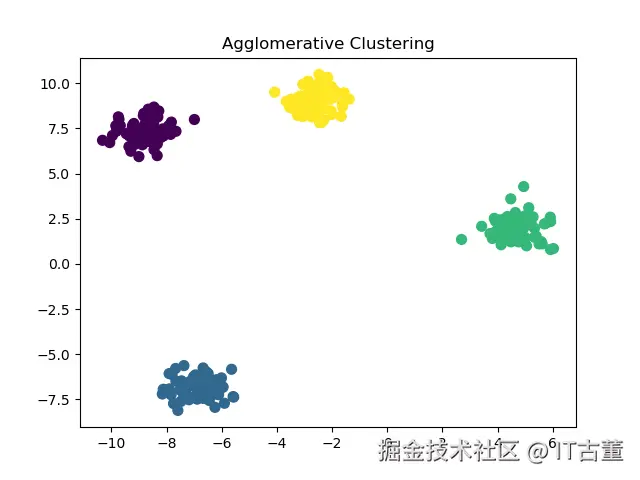

生成树状图（Dendrogram）

python 复制代码

from scipy.cluster.hierarchy import dendrogram, linkage
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs

X, _ = make_blobs(n_samples=300, centers=4, cluster_std=0.6, random_state=42)

# 生成层次聚类的链接矩阵
Z = linkage(X, method='ward')

# 绘制树状图
plt.figure(figsize=(10, 7))
dendrogram(Z)
plt.title('Dendrogram')
plt.xlabel('Sample Index')
plt.ylabel('Distance')
plt.show()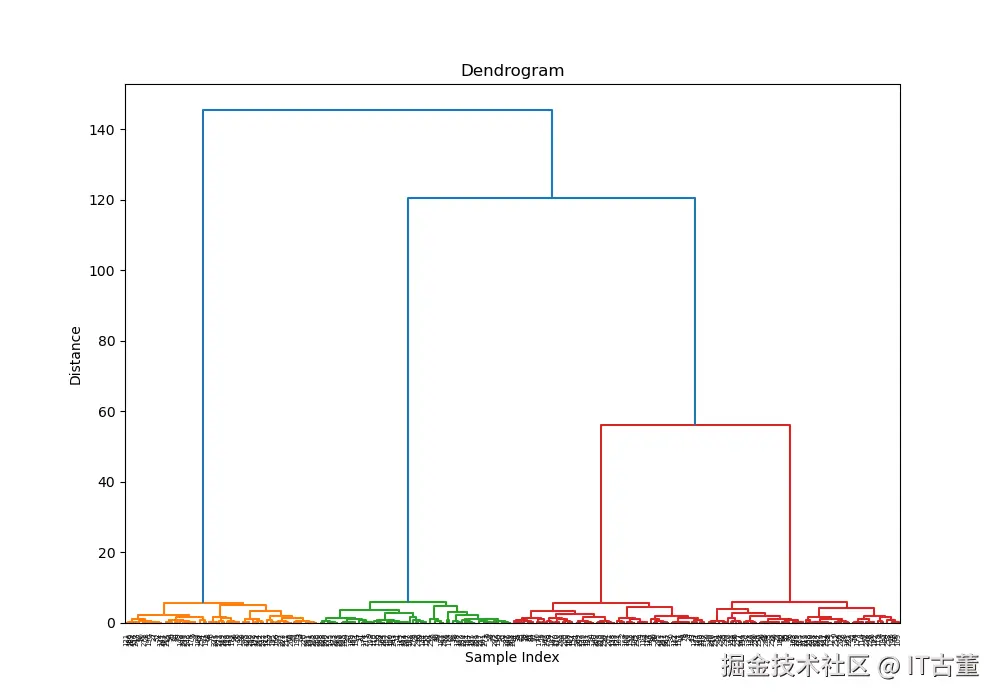

6. 应用场景

文本聚类：
- 将文档或短语按语义分层聚类。
基因聚类：
- 分析基因表达数据，寻找相似的基因组。
图像分割：
- 根据像素密度将图像划分为不同区域。
客户分群：
- 根据客户行为分层次聚类，细分市场。

7. 评价指标

轮廓系数 (Silhouette Coefficient)

衡量聚类效果，计算公式：

<math xmlns="http://www.w3.org/1998/Math/MathML"> s = b − a max ⁡ ( a , b ) s = \frac{b - a}{\max(a, b)} </math>s=max(a,b)b−a

a：样本点与同簇点的平均距离。
b：样本点与最近簇中点的平均距离。

CH 指数 (Calinski-Harabasz Index)

衡量簇间距离与簇内距离的比值，值越大效果越好。

树状图分析

观察树状图，选择合适的截断高度以确定簇数。

8. Agglomerative 与其他聚类算法对比

特性	Agglomerative Clustering	K-Means	DBSCAN
簇数量	自动或手动指定	需预设	自动确定
簇形状	任意形状	适用于凸形状	任意形状
计算复杂度	较高	较低	较高
适用场景	层次结构	大规模数据	噪声点多，簇密度明显

Agglomerative 聚类提供了强大的层次化信息展示能力，非常适合探索和分析小规模数据的内在结构。但在处理大规模数据时，计算复杂度较高，需要结合降维或加速算法使用。