力扣hot100：环形链表II（哈希算法与快慢指针法思路讲解）

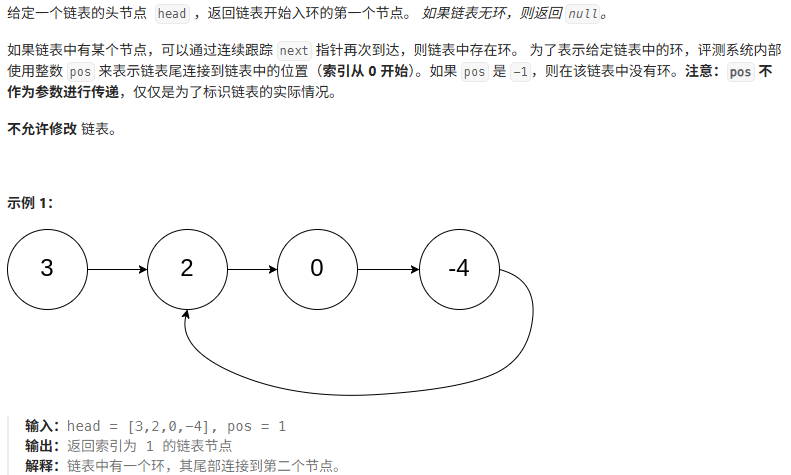
题目概述

方法一：哈希表法 - 直观空间换时间

思路分析

使用哈希表存储遍历过的节点，当遇到重复节点时，该节点即为环的入口。这种方法思路简单直接，利用了哈希表的快速查找特性。

代码实现

java 复制代码

public class Solution {
    public ListNode detectCycle(ListNode head) {
        ListNode pos = head;
        Set<ListNode> visited = new HashSet<>(); // 存储已访问节点
        while (pos != null) {
            if (visited.contains(pos)) { // 发现重复节点
                return pos; // 返回环的入口
            } else {
                visited.add(pos); // 记录访问过的节点
            }
            pos = pos.next; // 移动到下一个节点
        }
        return null; // 遍历结束无环
    }
}

复杂度分析

时间复杂度：O(n)。每个节点只需访问一次。
空间复杂度：O(n)。最坏情况下需要存储所有节点。

方法二：快慢指针法（Floyd 算法）- 空间高效的数学解法

思路分析

判断是否有环：使用快指针（每次两步）和慢指针（每次一步），若两指针相遇则有环
寻找环入口：相遇后将一个指针移回头部，两指针每次一步移动，再次相遇点即为环入口

数学证明

设：

头节点到环入口距离为 a
环入口到相遇点距离为 b
相遇点到环入口距离为 c
环长度：L = b + c

当快慢指针相遇时：

慢指针路程：a + b
快指针路程：a + b + kL（绕环 k 圈）
快指针路程 = 2 × 慢指针路程
2(a + b) = a + b + k(b + c)
化简得：a = (k-1)L + c

这表明：头节点到环入口距离 = 相遇点到环入口距离 + (k-1)圈环长，因此两指针将在环入口相遇。

代码实现

java 复制代码

public class Solution {
    public ListNode detectCycle(ListNode head) {
        ListNode slow = head;
        ListNode fast = head;
        
        while (fast != null) {
            // 快指针移动前的边界检查
            if (fast.next == null) {
                return null; // 无环
            }
            fast = fast.next.next; // 快指针移动两步
            slow = slow.next;      // 慢指针移动一步
            
            // 发现环时
            if (slow == fast) {
                ListNode temp = head; // 新指针从头出发
                // 两指针同步移动直到相遇
                while (temp != slow) {
                    temp = temp.next;
                    slow = slow.next;
                }
                return slow; // 返回环入口
            }
        }
        return null; // 遍历结束无环
    }
}

复杂度分析

时间复杂度：O(n)。线性遍历链表。
空间复杂度：O(1)。仅使用固定指针。

两种方法对比

方法	时间复杂度	空间复杂度	优势
哈希表法	O(n)	O(n)	实现简单，逻辑直观
快慢指针法	O(n)	O(1)	空间高效，数学原理精妙

总结

面试推荐：优先使用快慢指针法，尤其面试官关注空间复杂度时
实用场景：哈希表法在小规模数据或非性能关键场景更易实现
关键技巧：Floyd 算法的第二阶段（移动头指针与相遇点指针）是找到环入口的精髓

理解这两种解法不仅能解决本题，还能为解决其他链表环问题打下坚实基础。快慢指针法中蕴含的数学原理尤其值得深入体会！

掌握环形链表检测的核心思想，你就能轻松应对链表相关的各类环检测问题！