矩阵置零(LeetCode 73)
题目链接:矩阵置零(LeetCode 73)
难度:中等
1. 题目描述
给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法(不能用额外空间)。
要求:
- m == matrix.length
- n == matrix[0].length
- 1 <= m, n <= 200
- -2^31 <= matrix[i][j] <= 2^31 - 1
示例:
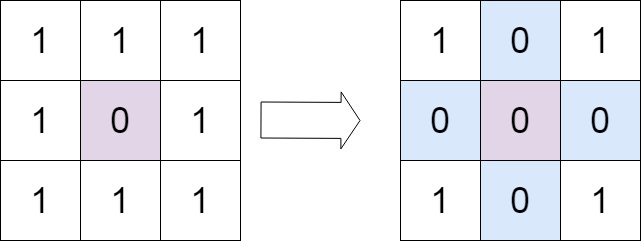
输入:matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出:[[1,0,1],[0,0,0],[1,0,1]]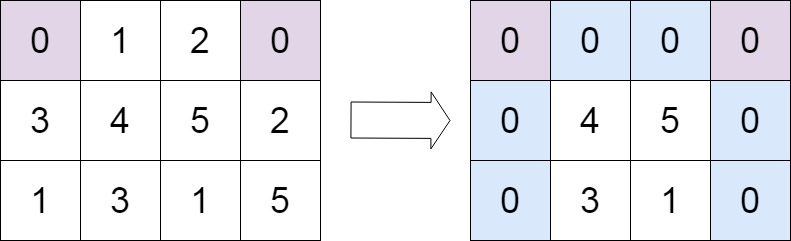
输入:matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出:[[0,0,0,0],[0,4,5,0],[0,3,1,0]]2. 问题分析
2.1 规律
想象矩阵像一张表格,如果某个格子是 0,就要把整行和整列的格子都变成 0。这像"零传染"一样,但不能用额外表格记录(因为要原地)。
简单说:先找所有 0 的位置,然后把那些行和列清零,但不能乱改数据,以免搞丢信息。
2.2 标记法思路
如果在某处遇到了0,最终都会传染到第一行和第一列,所以我们索性可以直接用矩阵的"边框"(第一行和第一列)来标记该行或列是否会被置零。
同时也要考虑到,边框里原本可能就有0,会把边框全部传染,所以我们应该先检查一下边框,如果真的有0则单独记录下来,最后把边框置零。
- 检查边框 :先看第一行有没有 0(记在
row0 = True),第一列有没有 0(记在col0 = True)。这样知道边框最后要不要清零。 - 找边框内部的0,并在边框上标记:从矩阵内(不碰边框)扫一遍。如果看到 0,就在边框上做标记:把这个0对应的行边框和列边框都标记为0,表示最终整行和整列都需要置0!
- 根据边框的0标记清零:从右下角开始扫(避免改了记号影响别人)。如果某行的边框标记是 0,就清整行;如果某列的边框标记是 0,就清整列。
- 最后清边框 :根据步骤1的
row0和col0,清第一行和第一列。
为什么从右下扫?因为记号在左上,改右下不会影响记号。
这样,只用两个小标志(row0 和 col0),空间 O(1)!
3. 代码实现
Python
python
class Solution:
def setZeroes(self, matrix):
if not matrix or not matrix[0]:
return
m, n = len(matrix), len(matrix[0])
row0 = any(matrix[0][j] == 0 for j in range(n)) # 第一行有0吗?
col0 = any(matrix[i][0] == 0 for i in range(m)) # 第一列有0吗?
# 步骤2:内里找0并标记边框
for i in range(1, m):
for j in range(1, n):
if matrix[i][j] == 0:
matrix[i][0] = 0 # 标记行
matrix[0][j] = 0 # 标记列
# 步骤3:从右下扫,根据标记清零
for i in range(m-1, 0, -1): # 从下往上扫行
if matrix[i][0] == 0: # 这行要清
for j in range(n-1, -1, -1): # 清整行,从右到左
matrix[i][j] = 0
for j in range(n-1, 0, -1): # 从右往左扫列
if matrix[0][j] == 0: # 这列要清
for i in range(m-1, -1, -1): # 清整列,从下到上
matrix[i][j] = 0
# 步骤4:清边框
if row0:
for j in range(n):
matrix[0][j] = 0
if col0:
for i in range(m):
matrix[i][0] = 0C++
cpp
class Solution {
public:
void setZeroes(vector<vector<int>>& matrix) {
if (matrix.empty() || matrix[0].empty()) return;
int m = matrix.size();
int n = matrix[0].size();
bool row0 = false; // 第一行有0吗?
bool col0 = false; // 第一列有0吗?
// 步骤1:检查边框
for (int j = 0; j < n; ++j) {
if (matrix[0][j] == 0) { row0 = true; break; }
}
for (int i = 0; i < m; ++i) {
if (matrix[i][0] == 0) { col0 = true; break; }
}
// 步骤2:内里找0并标记
for (int i = 1; i < m; ++i) {
for (int j = 1; j < n; ++j) {
if (matrix[i][j] == 0) {
matrix[i][0] = 0; // 标记行
matrix[0][j] = 0; // 标记列
}
}
}
// 步骤3:从右下扫清零
for (int i = m - 1; i >= 1; --i) {
if (matrix[i][0] == 0) {
for (int j = n - 1; j >= 0; --j) {
matrix[i][j] = 0;
}
}
}
for (int j = n - 1; j >= 1; --j) {
if (matrix[0][j] == 0) {
for (int i = m - 1; i >= 0; --i) {
matrix[i][j] = 0;
}
}
}
// 步骤4:清边框
if (row0) {
fill(matrix[0].begin(), matrix[0].end(), 0);
}
if (col0) {
for (int i = 0; i < m; ++i) {
matrix[i][0] = 0;
}
}
}
};4. 复杂度分析
- 时间复杂度:O(mn),扫几遍矩阵,但总共就这么多格子
- 空间复杂度:O(1),只用两个 bool 变量
5. 总结
- 原地清零 → 用边框当"便签"记位置,超聪明!
- 记住顺序:检查 → 标记 → 清内 → 清边。一步错,全乱
- 如果矩阵很大,时间够用;小矩阵直接试试看效果
6、复习
面试经典150题[007]:买卖股票的最佳时机(LeetCode 121)
面试经典150题[022]:Z 字形变换(LeetCode 6)