目录
[一、#172269 knn算法](#172269 knn算法)
[二、#172385 k-mean算法](#172385 k-mean算法)
[三、#172363 FM指数计算](#172363 FM指数计算)
[四、#172364 兰德指数](#172364 兰德指数)
[五、#172365 轮廓系数](#172365 轮廓系数)
[六、#172372 DBSCAN算法](#172372 DBSCAN算法)
一、#172269 knn算法
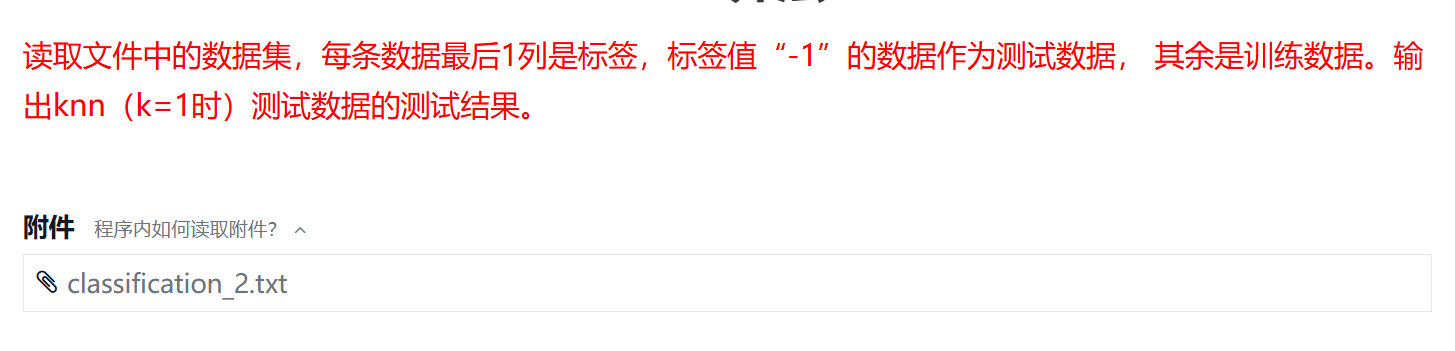
python
import numpy as np
#将数据集划分为训练集、标签和测试集
def split_data(data):
# 最后一列是标签
labels = data[:, -1]
# 标签为 -1 的是测试数据
test_mask = labels == -1
train_mask = ~test_mask
x_train = data[train_mask, :-1]
y_train = labels[train_mask]
x_test = data[test_mask, :-1]
return x_train, x_test, y_train
#输入参数:训练集数据,训练集标签,1条测试数据;输出预测的标签
def knn(x_train, y_train, test_x):
# 计算欧氏距离
distances = np.linalg.norm(x_train - test_x, axis=1)
# 找到最近邻的索引
nearest_idx = np.argmin(distances)
# 返回对应的标签
return int(y_train[nearest_idx])
if __name__ == '__main__':
data = np.loadtxt('classification_2.txt')
x_train, x_test, y_train = split_data(data)
for i in range(len(x_test)):
print(knn(x_train, y_train, x_test[i]), end=' ')
return int(y_train[nearest_idx])二、#172385 k-mean算法
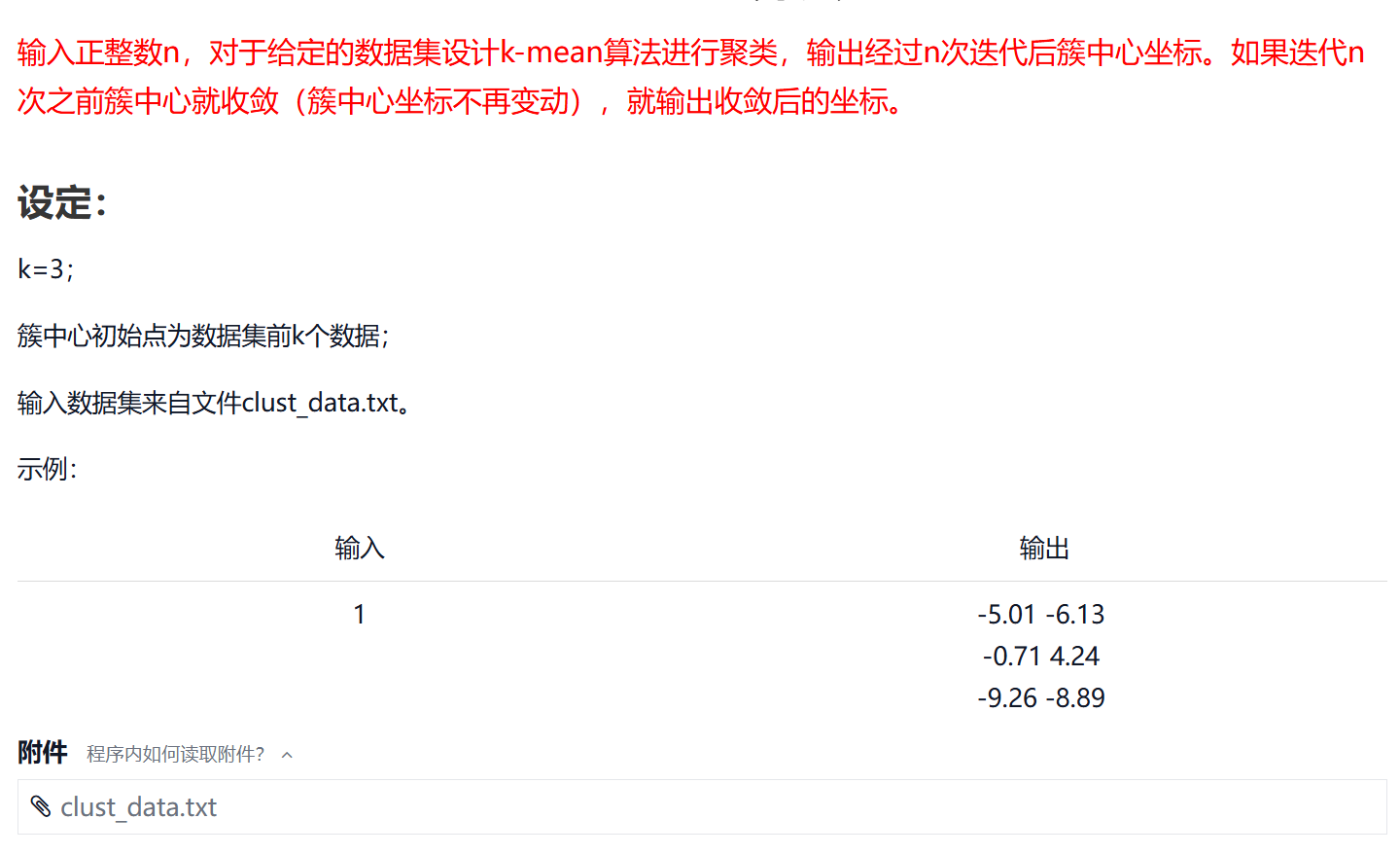
python
import numpy as np
#输入参数 x:数据集,n:迭代次数;输出:簇中心坐标
def k_means(x, n):
row, _ = x.shape
centers = x[:k]
y = np.zeros(row, dtype=int)
counter = 0
while counter < n:
counter += 1
for i in range(row):
min_id = -1
min_dist = np.inf
for j in range(k):
distance = np.power(x[i] - centers[j], 2).sum()
if distance < min_dist:
min_id = j
min_dist = distance
if y[i] != min_id:
y[i] = min_id
for i in range(k):
centers[i, :] = np.mean(x[y == i], axis=0)
return centers
if __name__ == '__main__':
k = 3
data = np.loadtxt('clust_data.txt')
n = int(input())
centers = k_means(data, n)
for i in centers:
for j in i:
print('{:.2f}'.format(j), end=' ')
print()三、#172363 FM指数计算

python
def fowlkes_mallows(y1, y2):
# 确保两个标签列表长度相同
assert len(y1) == len(y2), "两个标签列表长度必须相同"
n = len(y1)
tp = 0 # 真正例:同一类且被聚在同一簇
fp = 0 # 假正例:不同类但被聚在同一簇
fn = 0 # 假负例:同一类但被聚在不同簇
# 遍历所有样本对
for i in range(n):
for j in range(i + 1, n):
# 判断是否为同一类
same_class = (y1[i] == y1[j])
# 判断是否被聚在同一簇
same_cluster = (y2[i] == y2[j])
if same_class and same_cluster:
tp += 1
elif not same_class and same_cluster:
fp += 1
elif same_class and not same_cluster:
fn += 1
# 计算精度和召回率
precision = tp / (tp + fp) if (tp + fp) > 0 else 0
recall = tp / (tp + fn) if (tp + fn) > 0 else 0
# 计算FM指数
return (precision * recall) **0.5 if (precision * recall) >= 0 else 0
if __name__ == '__main__':
y_true = [2, 2, 1, 2, 1, 0, 2, 0, 0, 1, 2, 0, 0, 2, 0, 2, 1, 0, 1, 0]
# 读取输入的预测标签
input_str = input().strip()
y_pred = list(map(int, input_str.split(',')))
score = fowlkes_mallows(y_true, y_pred)
print('{:.4f}'.format(score))四、#172364 兰德指数
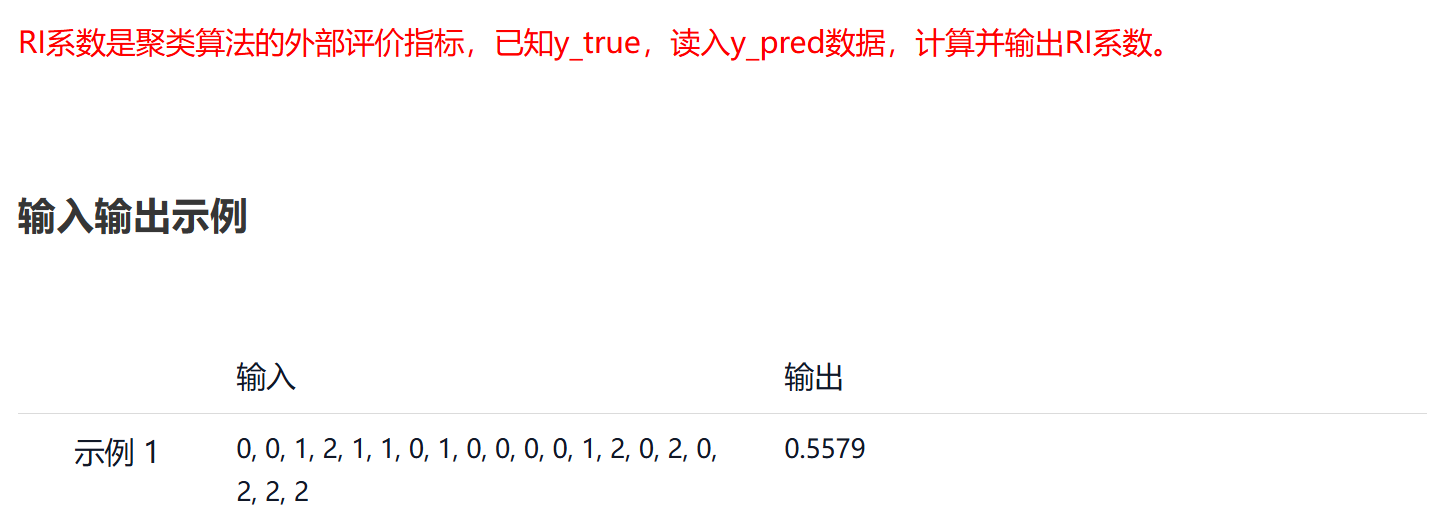
python
def rand_score(y1, y2):
# 确保两个标签列表长度相同
assert len(y1) == len(y2), "两个标签列表长度必须相同"
n = len(y1)
tp = 0 # 真正例:同一类且被聚在同一簇
tn = 0 # 真负例:不同类且被聚在不同簇
total_pairs = n * (n - 1) // 2 # 总样本对数量
# 遍历所有样本对
for i in range(n):
for j in range(i + 1, n):
# 判断是否为同一类
same_class = (y1[i] == y1[j])
# 判断是否被聚在同一簇
same_cluster = (y2[i] == y2[j])
if same_class and same_cluster:
tp += 1
elif not same_class and not same_cluster:
tn += 1
# 计算兰德指数
return (tp + tn) / total_pairs if total_pairs > 0 else 0
if __name__ == '__main__':
y_true = [2, 2, 1, 2, 1, 0, 2, 0, 0, 1, 2, 0, 0, 2, 0, 2, 1, 0, 1, 0]
# 读取输入的预测标签
input_str = input().strip()
y_pred = list(map(int, input_str.split(',')))
score = rand_score(y_true, y_pred)
print('{:.4f}'.format(score))五、#172365 轮廓系数
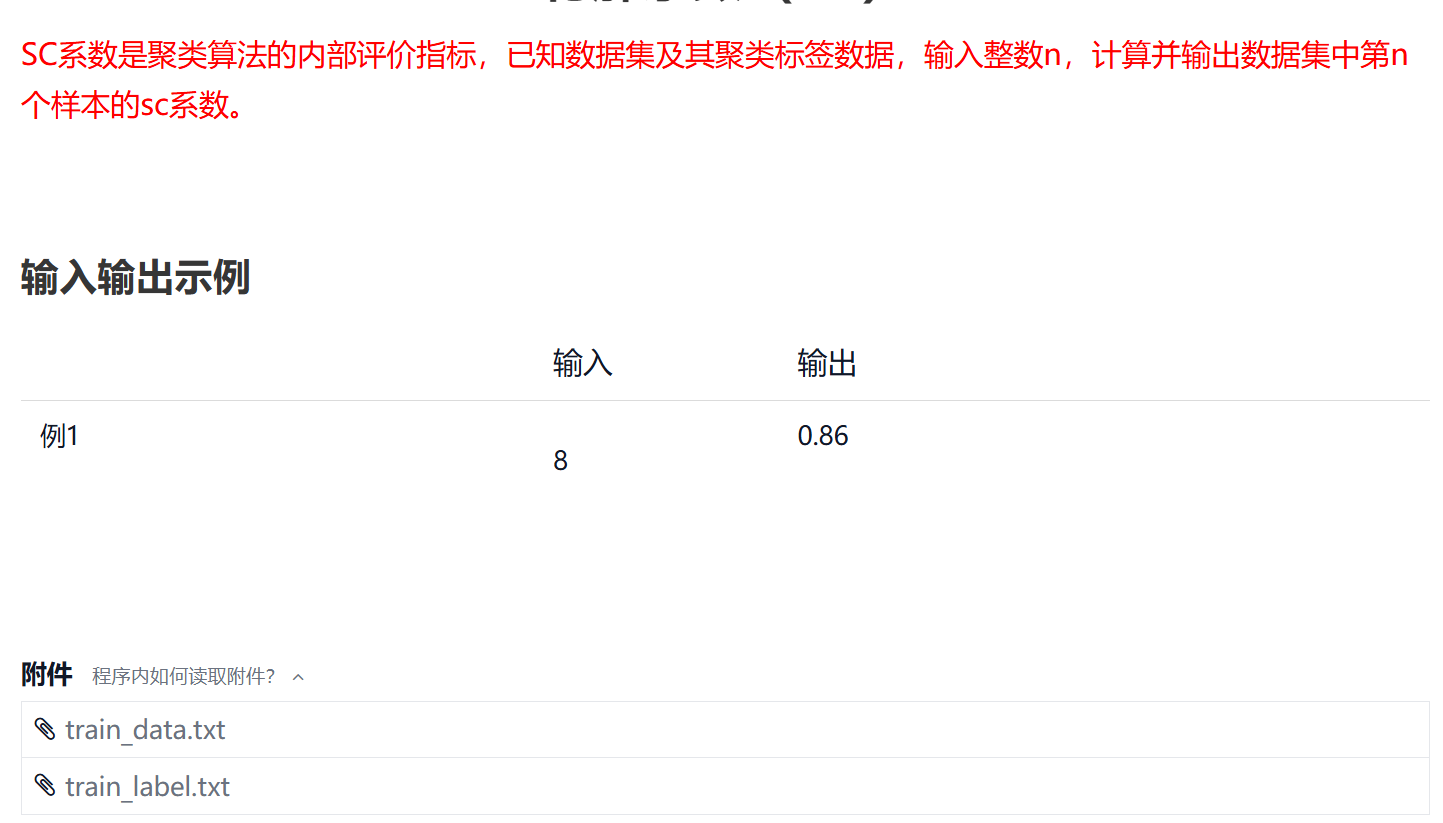
python
import numpy as np
#输入参数 x:数据集,y:聚类结果,n:样本序号;输出 样本n的轮廓系数
def sc(x, y, n):
# 获取第n个样本的数据和其所属簇
sample = x[n]
cluster = y[n]
# 获取同一簇中的其他样本
same_cluster = x[y == cluster]
# 如果簇中只有一个样本,轮廓系数定义为0
if len(same_cluster) <= 1:
return 0.0
# 计算a:与同一簇内其他所有样本的平均距离
distances_same = np.sqrt(np.sum((same_cluster - sample) **2, axis=1))
a = np.mean(distances_same[distances_same > 0]) # 排除与自身的距离
# 计算b:与最近不同簇中所有样本的平均距离
clusters = np.unique(y)
min_avg_distance = float('inf')
for c in clusters:
if c != cluster:
# 获取当前其他簇的所有样本
other_cluster = x[y == c]
# 计算到该簇所有样本的平均距离
distances_other = np.sqrt(np.sum((other_cluster - sample)** 2, axis=1))
avg_distance = np.mean(distances_other)
# 记录最小的平均距离
if avg_distance < min_avg_distance:
min_avg_distance = avg_distance
b = min_avg_distance
# 计算轮廓系数
if max(a, b) == 0:
return 0.0
return (b - a) / max(a, b)
if __name__ == '__main__':
X = np.loadtxt('train_data.txt')
labels = np.loadtxt('train_label.txt')
n = int(input())
print('{:.2f}'.format(sc(X, labels, n)))六、#172372 DBSCAN算法
python
import numpy as np
#创建邻接矩阵 输入参数x:样本集 输出:邻接表
def dist_table(x):
"""
计算距离邻接表
返回 list,第 i 项为与样本 i 距离 ≤ eps 的所有样本编号(含自身)
"""
n = x.shape[0]
table = [[] for _ in range(n)]
for i in range(n):
dists = np.linalg.norm(x - x[i], axis=1)
table[i] = np.where(dists <= eps)[0].tolist()
return table
#需要调用的函数
def _dfs_expand(i, table, visited, y_pred, cluster_id):
"""
从核心点 i 出发,深度优先扩簇
"""
y_pred[i] = cluster_id
visited[i] = True
for j in table[i]: # 遍历 ε-邻域
if not visited[j]:
visited[j] = True
y_pred[j] = cluster_id
# 若 j 也是核心点,继续递归
if len(table[j]) >= minpts:
_dfs_expand(j, table, visited, y_pred, cluster_id)
#输入参数 x:训练集;输出 将聚类结果放在y_pred中
def dbscan(x):
"""
聚类结果直接写入全局 y_pred 数组
"""
n = x.shape[0]
global y_pred
y_pred[:] = -1 # -1 表示噪声
visited = np.zeros(n, dtype=bool)
table = dist_table(x) # 邻接表
cluster_id = 0
for i in range(n):
if visited[i]:
continue
# 必须是核心点才能创建新簇
if len(table[i]) >= minpts:
_dfs_expand(i, table, visited, y_pred, cluster_id)
cluster_id += 1
# 非核心点保留 -1(噪声或边界点)
eps = 0.2
minpts = 5
X = np.loadtxt('moon_data.txt')
y_pred = np.full(len(X), -1, dtype=int)
adj_table = dist_table(X)
dbscan(X)
for i in y_pred:
print(i, end=' ')七、#217674
python
import numpy as np
#输入参数 x:数据集,k:簇心数量,n:第1个簇心序号;输出:簇中心列表
def clu_centers(x, k, n):
row, _ = x.shape
centers = [n]
while len(centers) < k:
max_dist = 0
max_id = 0
for i in range(row):
min_dis = np.inf
if i not in centers:
for j in centers:
dist = np.power(x[i] - x[j], 2).sum()
if min_dis > dist:
min_dis = dist
if max_dist < min_dis:
max_dist = min_dis
max_id = i
centers.append(max_id)
return centers
if __name__ == '__main__':
k = 3
data = np.loadtxt('clust_data.txt')
n = int(input())
centers = clu_centers(data, k, n)
for i in centers:
if i != n:
print(i, end=' ')