锋哥原创的Scikit-learn Python机器学习视频教程:
https://www.bilibili.com/video/BV11reUzEEPH
课程介绍

本课程主要讲解基于Scikit-learn的Python机器学习知识,包括机器学习概述,特征工程(数据集,特征抽取,特征预处理,特征降维等),分类算法(K-临近算法,朴素贝叶斯算法,决策树等),回归与聚类算法(线性回归,欠拟合,逻辑回归与二分类,K-means算法)等。
Scikit-learn Python机器学习 - 回归分析算法 - 弹性网络 (Elastic-Net)
弹性网络(Elastic Net)是一种结合了L1(Lasso)和L2(Ridge)正则化的线性回归方法。它通过同时使用L1和L2正则化项,克服了Lasso和Ridge回归各自的一些局限性,特别适用于特征数量远大于样本数量(p >> n)或者特征高度相关的情况。
基本数学原理
弹性网络回归的目标函数如下:

- 最小二乘误差(Residual Sum of Squares, RSS)
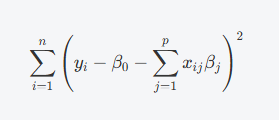
这是弹性网络回归中的误差项,和普通最小二乘回归相同,表示模型的拟合误差。
-
L1正则化项(Lasso)
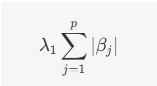
这是L1正则化项,作用是通过惩罚回归系数的绝对值,使得一些回归系数趋向于零,从而实现特征选择。它使得模型具备稀疏性(即部分特征的系数为零),特别适合特征数量较多的情况。
-
L2正则化项(Ridge)
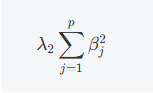
这是L2正则化项,作用是通过惩罚回归系数的平方,使得回归系数趋向于较小的数值,防止模型过拟合。与L1正则化不同,L2正则化不会将回归系数压缩为零,而是将它们的绝对值缩小。
- 弹性网络的组合
弹性网络回归通过同时引入 L1 正则化和 L2 正则化,综合了 Lasso 和 Ridge 的优点:
-
Lasso(L1正则化)能够通过将一些回归系数推向零来实现特征选择,特别适合高维数据集。
-
Ridge(L2正则化)可以处理多重共线性(特征之间高度相关)问题,能够将回归系数压缩至较小的值,而不是将其置零。
API介绍
ElasticNet 是结合了 L1(Lasso)和 L2(Ridge)正则化的线性回归模型,适用于处理特征选择和多共线性问题。
ElasticNet(alpha=1.0, l1_ratio=0.5, fit_intercept=True,
max_iter=1000, tol=1e-4, random_state=None)核心参数:
1. alpha - 正则化强度
-
作用: 控制整体正则化的强度
-
默认值: 1.0
-
范围: 正浮点数,值越大正则化越强
2. l1_ratio - L1/L2 混合比例
-
作用: 控制L1和L2正则化的混合比例
-
默认值: 0.5
-
范围: 0.0 到 1.0
-
0.0 = 纯Ridge回归
-
1.0 = 纯Lasso回归
-
0.5 = 均等混合
-
3. fit_intercept - 截距计算
-
作用: 是否计算模型的截距项
-
默认值: True
-
建议: 通常保持为True
4. max_iter - 最大迭代次数
-
作用: 优化算法的最大迭代次数
-
默认值: 1000
-
调整: 复杂问题需要增加此值
5. tol - 收敛精度
-
作用: 优化的停止准则
-
默认值: 1e-4
-
调整: 更小的值=更高精度但更慢
具体示例-加州房价预测
from sklearn.datasets import fetch_california_housing
from sklearn.linear_model import SGDRegressor, Ridge, ElasticNet
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
# 1,加载数据
california = fetch_california_housing()
print(california.data, california.data.shape)
print(california.target)
print(california.feature_names)
# 2,数据预处理
X_train, X_test, y_train, y_test = train_test_split(california.data, california.target, test_size=0.2, random_state=20)
scaler = StandardScaler() # 数据标准化:消除不同特征量纲的影响
X_train_scaled = scaler.fit_transform(X_train) # fit计算生成模型,transform通过模型转换数据
X_test_scaled = scaler.transform(X_test) # # 使用训练集的参数转换测试集
# 3,创建和训练模型
en_model = ElasticNet() # 创建分类器实例
en_model.fit(X_train_scaled, y_train) # 训练模型
print('权重系数:', en_model.coef_)
print('偏置值:', en_model.intercept_)
# 4,模型评估
y_predict = en_model.predict(X_test_scaled)
print('预测值:', y_predict)
mse = mean_squared_error(y_test, y_predict)
print('梯度下降方程-均方误差:', mse)运行结果:
[[ 8.3252 41. 6.98412698 ... 2.55555556
37.88 -122.23 ]
[ 8.3014 21. 6.23813708 ... 2.10984183
37.86 -122.22 ]
[ 7.2574 52. 8.28813559 ... 2.80225989
37.85 -122.24 ]
...
[ 1.7 17. 5.20554273 ... 2.3256351
39.43 -121.22 ]
[ 1.8672 18. 5.32951289 ... 2.12320917
39.43 -121.32 ]
[ 2.3886 16. 5.25471698 ... 2.61698113
39.37 -121.24 ]] (20640, 8)
[4.526 3.585 3.521 ... 0.923 0.847 0.894]
['MedInc', 'HouseAge', 'AveRooms', 'AveBedrms', 'Population', 'AveOccup', 'Latitude', 'Longitude']
权重系数: [ 0.19036127 0. 0. -0. -0. -0.
-0. -0. ]
偏置值: 2.0678235537790717
预测值: [1.94658326 2.30453906 1.88139745 ... 2.09554362 2.24239959 1.89894401]
梯度下降方程-均方误差: 1.115958465902034