归并排序算法
python
# 定义归并排序函数:对数组arr进行排序
def merge_sort(arr):
# 递归终止条件:如果数组长度小于等于1,说明已经是有序的,直接返回
if len(arr) <= 1:
return arr
# 计算中间索引,将数组分成左右两部分(二分法)
mid = len(arr) // 2 # 整除操作,确保索引为整数
left = arr[:mid] # 左半部分:从开始到mid-1(不包含mid)
right = arr[mid:] # 右半部分:从mid到结束
# 递归对左右两部分进行归并排序(分治思想)
left_sorted = merge_sort(left) # 对左半部分排序
right_sorted = merge_sort(right) # 对右半部分排序
# 合并两个已排序的子数组,返回最终结果
return merge(left_sorted, right_sorted)
# 定义合并函数:将两个已排序的数组left和right合并成一个有序数组
def merge(left, right):
result = [] # 创建一个空列表,用于存储合并后的结果
i = j = 0 # 初始化指针:i指向left数组的起始位置,j指向right数组的起始位置
# 比较左右两个数组的元素,按从小到大的顺序放入结果数组
# 循环条件:两个数组都还有未比较的元素
while i < len(left) and j < len(right):
# 如果left当前元素小于等于right当前元素
if left[i] <= right[j]:
result.append(left[i]) # 将left当前元素加入结果数组
i += 1 # 移动左指针,指向left的下一个元素
else:
result.append(right[j]) # 将right当前元素加入结果数组
j += 1 # 移动右指针,指向right的下一个元素
# 当left数组还有剩余元素时,将剩余元素全部加入结果数组
# (此时right数组已遍历完,剩余元素直接拼接)
result.extend(left[i:])
# 当right数组还有剩余元素时,将剩余元素全部加入结果数组
# (此时left数组已遍历完,剩余元素直接拼接)
result.extend(right[j:])
return result # 返回合并后的有序数组
# 测试代码
arr = [10, 6, 7, 1, 3, 9, 4, 2] # 定义一个待排序的数组
sorted_arr = merge_sort(arr) # 调用归并排序函数
print(sorted_arr) # 输出排序结果:[1, 2, 3, 4, 6, 7, 9, 10]循环过程中数组的变化分析(以测试用例[10,6,7,1,3,9,4,2]为例):
分解阶段(merge_sort 函数的递归拆分):
初始数组:[10,6,7,1,3,9,4,2]
第一次拆分:left=[10,6,7,1],right=[3,9,4,2]
第二次拆分:
left再拆分为[10,6]和[7,1]
right再拆分为[3,9]和[4,2]
第三次拆分(直到数组长度为 1):
10,6\]→\[10\]和\[6
7,1\]→\[7\]和\[1
3,9\]→\[3\]和\[9
4,2\]→\[4\]和\[2
合并阶段(merge 函数的操作):
合并[10]和[6]:
比较 10 和 6→取 6,j=1→right 遍历完→拼接 left 剩余元素→结果[6,10]
合并[7]和[1]:
比较 7 和 1→取 1,j=1→right 遍历完→拼接 left 剩余元素→结果[1,7]
合并[6,10]和[1,7]:
比较 6 和 1→取 1,j=1
比较 6 和 7→取 6,i=1
比较 10 和 7→取 7,j=2→right 遍历完→拼接 left 剩余元素→结果[1,6,7,10]
合并[3]和[9]→[3,9](类似上述过程)
合并[4]和[2]→[2,4](类似上述过程)
合并[3,9]和[2,4]→[2,3,4,9](类似上述过程)
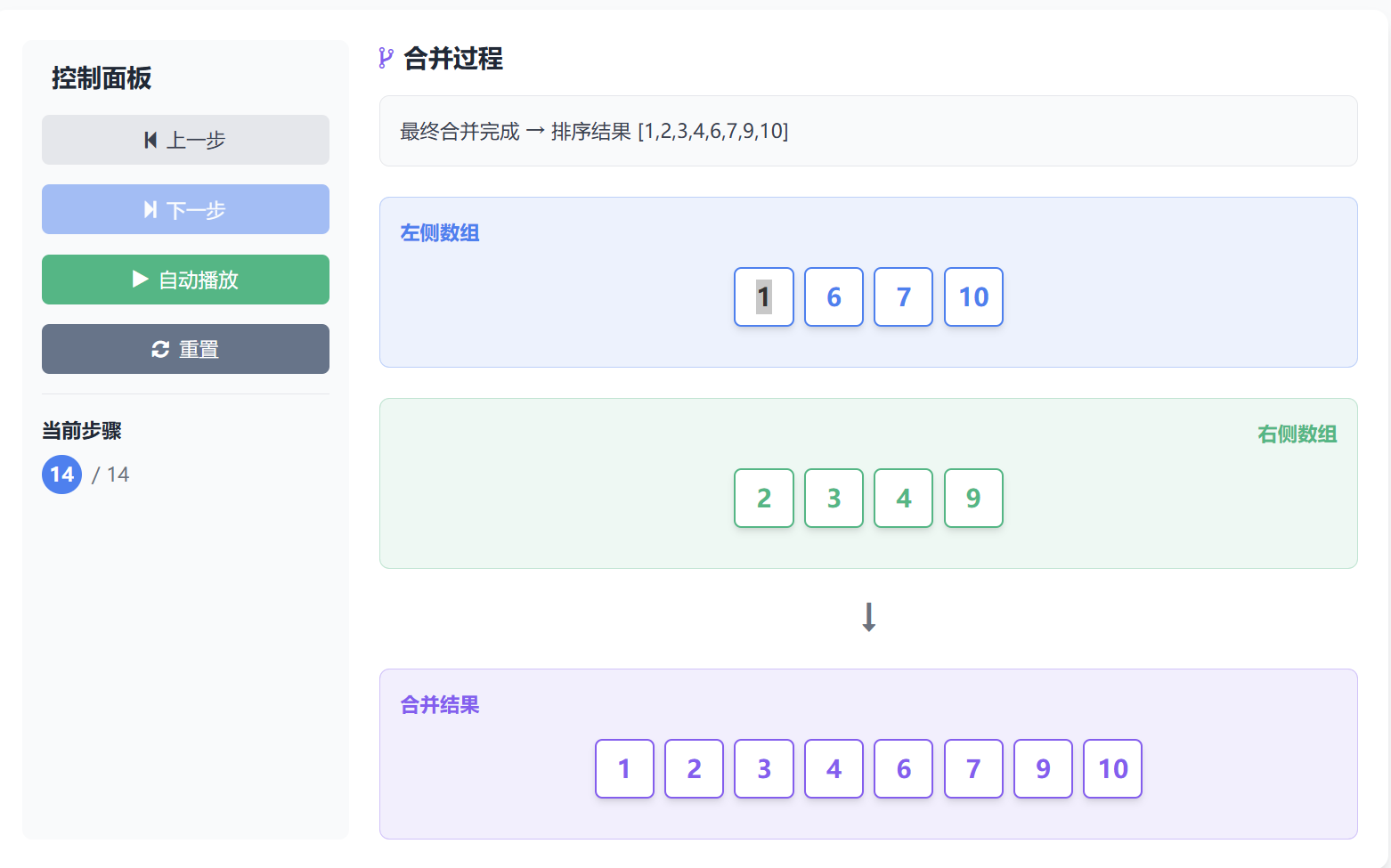
最终合并[1,6,7,10]和[2,3,4,9]→[1,2,3,4,6,7,9,10]
演示过程: