前言
传统的机器人控制方法依赖于精确的物理模型和复杂的数学公式,然而足式机器人面临几个固有难题:
- 机器人具有高度复杂的非线性动力学模型
- 应用场景存在大量不确定性
- 关节数量多,状态和动作的空间维度很高
与传统方法不同,强化学习可以不依赖于精确的模型,而是通过智能体与环境的不断交互,从试错中学习最优策略,从而适应各种复杂和未知的环境。随着强化学习的发展,人们发现了其在足式机器人上应用的可能性,并超越了许多传统方法,因而足式机器人与强化学习的结合成为当前机器人领域最前沿和活跃的研究方向之一。
尽管强化学习可以抛开物理模型,基于纯粹的计算机科学,但引入动力学模型作为先验信息将在一定程度上提升强化学习的训练效果。足式机器人的动力学模型及其与强化学习的结合将在具有一定强化学习算法基础后进行补充。
本系列学习笔记中强化学习以及其他可能会遇到的前置知识的介绍主要以为足式机器人算法铺路为目的,不会系统性全面展开,更基础的强化学习还请见【强化学习】系列笔记。在本篇简要回顾强化学习的核心概念之后博主将直接进行机器人领域主流强化学习算法的学习分享。
定义
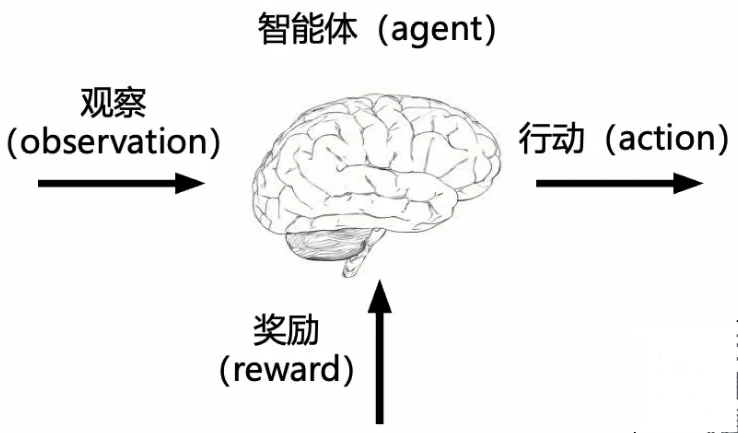
强化学习是通过从交互中学习来实现目标的计算方法,主要包括三个方面
- 感知:在某种程度上感知环境的状态
- 行动:可以采取行动来影响状态或者达到目标
- 目标:随着时间推移最大化累积奖励
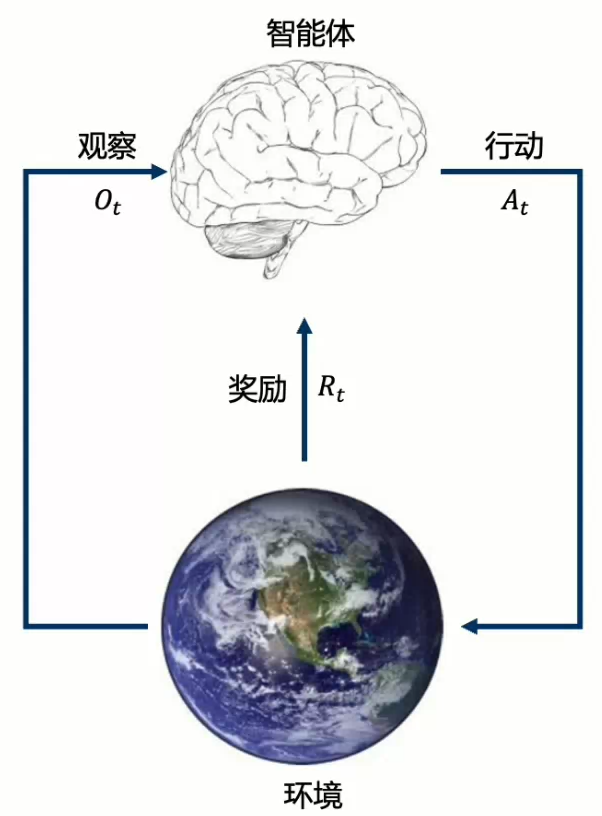
在强化学习的每一步ttt中,智能体和环境将按如下流程运行
- 智能体
- 获得观察OtO_tOt
- 获得奖励RtR_tRt
- 执行行动AtA_tAt
- 环境
- 获得行动AtA_tAt
- 到达下一步t+1t+1t+1
- 给出观察Ot+1O_{t+1}Ot+1
- 给出奖励Rt+1R_{t+1}Rt+1
系统要素
历史 (History)是观察、行动和奖励的序列,即一直到时间ttt为止的所有可观测变量
Ht=O1,R1,A1,O2,R2,A2,⋯ ,Ot−1,Rt−1,At−1,Ot,Rt H_t=O_1,R_1,A_1,O_2,R_2,A_2,\cdots,O_{t-1},R_{t-1},A_{t-1},O_t,R_t Ht=O1,R1,A1,O2,R2,A2,⋯,Ot−1,Rt−1,At−1,Ot,Rt
- 历史可以影响接下来智能体如何选择行动以及环境如何选择观察和奖励。
状态(State)是一种用于确定接下来会发生的事情(行动、观察、奖励)的信息,是关于历史的函数
St=f(Ht) S_t=f(H_t) St=f(Ht)
策略(Policy)是智能体在特定时间的行为方式,是从状态到行动的映射
- 确定性策略(Deterministic Policy):a=π(s)a=\pi(s)a=π(s)
- 随机策略(Stochastic Policy):π(a∣s)=P(At=a∣St=s)\pi(a|s)=P(A_t=a|S_t=s)π(a∣s)=P(At=a∣St=s)
奖励 (Reward)R(s,a)R(s,a)R(s,a)是一个定义强化学习目标的标量,让智能体立即感知到什么是"好"的。
价值函数(Value Function)
- 状态价值是一个标量,用于定义对于长期来说什么是"好"的。
- 价值函数是对于未来累积奖励的预测,用于评估在给定的策略下状态的好坏
Qπ(s,a)=Eπ[Rt+1+γRt+2+γ2Rt+3+⋯∣St=s,At=a]=Eπ[Rt+1+γQπ(s′,a′)∣St=s,At=a] \begin{equation}\begin{split}Q_\pi(s,a)&=\mathbb E_\pi[R_{t+1}+\gamma R_{t+2}+\gamma^2R_{t+3}+\cdots|S_t=s,A_t=a]\\&=\mathbb E_\pi[R_{t+1}+\gamma Q_\pi(s',a')|S_t=s,A_t=a]\end{split}\end{equation} Qπ(s,a)=Eπ[Rt+1+γRt+2+γ2Rt+3+⋯∣St=s,At=a]=Eπ[Rt+1+γQπ(s′,a′)∣St=s,At=a]
环境的模型(Model)用于模拟环境的行为
- 预测下一个状态
- Ps,s′a=P[St+1=s′∣St=s,At=a]\mathcal P^a_{s,s'}=\mathbb P[S_{t+1}=s'|S_t=s,A_t=a]Ps,s′a=P[St+1=s′∣St=s,At=a]
- 预测下一个奖励
- Rsa=E[Rt+1∣St=s,At=a]\mathcal R^a_s=\mathbb E[R_{t+1}|S_t=s,A_t=a]Rsa=E[Rt+1∣St=s,At=a]
方法分类
价值与策略
- 基于价值:采取隐含的、确定的策略,以价值函数为学习目标
- 基于策略:绕过价值函数,直接学习策略函数
- Actor-Critic方法:结合基于价值与基于策略的混合方法,Actor负责执行策略,Critic负责评估策略表现,同时学习策略函数和价值函数
模型相关与无关
- 模型相关:智能体完全知道环境的动态模型,可以通过内部模拟规划直接计算价值和策略
- 模型无关:智能体不知道环境的模型,必须通过直接与环境交互,从真实的经验中学习
表格与近似
- 表格法:使用表格存储状态、动作和价值,适用于中小规模的状态/动作空间
- 近似法:使用参数化的函数来近似价值函数或策略函数,能处理大规模、连续的状态/动作空间
- 深度强化学习:利用深度神经网路进行价值函数和策略近似,从而使强化学习算法能够以端到端的方式解决复杂问题
算法分类
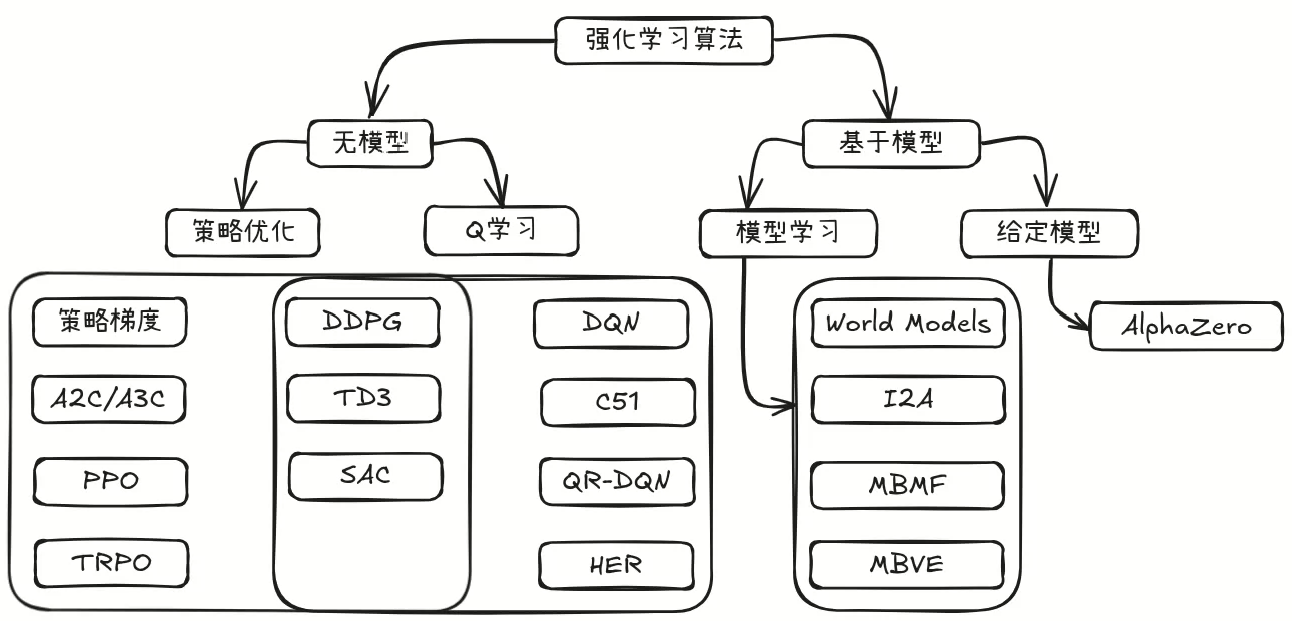
上图给出了现今主流的强化学习算法分类框架,以便读者自主了解与学习,博主后续将结合自身学习路线对其中的部分算法进行介绍。