深度学习（十三）：向量化与矩阵化

核心原理与意义

深度学习模型，无论多复杂，本质上都是在进行大量的线性代数运算 （如矩阵乘法、加法）和非线性激活函数 的应用。向量化和矩阵化的目的，就是将这些重复的、针对单个数据点或单个特征的操作，转化为针对整个批次数据 或整个特征集合 的高维代数运算。

传统编程中，我们可能会使用 for 循环 来遍历数据集中的每一个样本，然后对每个样本执行相同的计算（如 predict(xi)=W⋅xi+b）。当数据集包含数百万甚至数十亿个样本时，这种逐个处理的方式（即 标量操作）会非常耗时。

向量化和矩阵化通过以下方式解决了这个问题：

硬件加速的利用： 现代计算机的 CPU （中央处理器）和 GPU （图形处理器）都内置了专门用于并行处理数据的硬件单元。
- CPU 有 SIMD（Single Instruction, Multiple Data，单指令多数据）指令集（如 x86 架构的 AVX、SSE），允许一个指令同时操作多个数据元素（即向量）。
- GPU 天生就是为大规模并行计算设计的，拥有数千个计算核心，尤其擅长处理大规模的矩阵和向量运算。
消除 Python 循环的开销： 在像 Python 这样的高级语言中，for 循环的执行速度相对较慢，因为每次迭代都需要解释器进行额外的操作。将操作转移到 NumPy 或 TensorFlow/PyTorch 等底层库的内置函数中，这些函数通常是用 C/C++ 编写并高度优化的，可以直接调用底层的 SIMD 或 GPU 核函数，从而避免了高阶语言循环的性能瓶颈。

向量化后的代码更加简洁、清晰 ，能够更直接地反映底层的数学原理。例如，一个完整的批量梯度下降（Batch Gradient Descent）的步骤，在向量化后可以表达为寥寥几行代码，而使用 for 循环可能需要几十行。这种简洁性极大地提高了代码的可维护性 和可读性。

向量化 主要指将对单个特征 或单个样本 的操作扩展到对所有特征 或所有样本的操作。

标量操作 (非向量化):

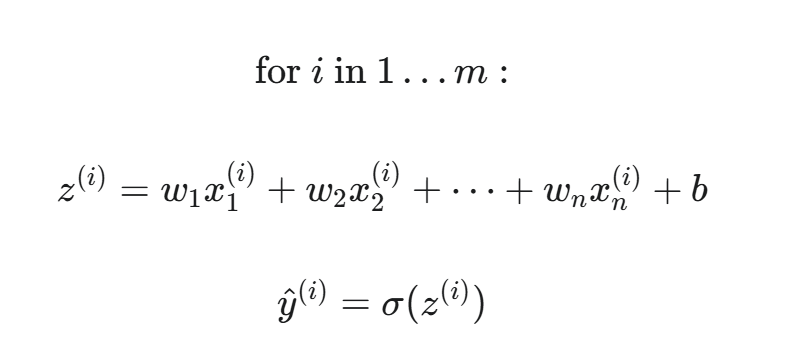
向量化 (针对单个样本的所有特征):

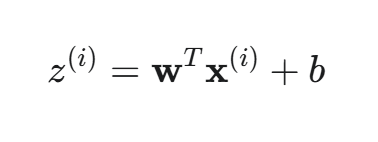
这里，w 和 x(i) 都是 n 维向量。一次运算计算了一个样本的全部特征的加权和。

若要对一个向量 Z 中的每个元素 zi 应用 σ(zi)，向量化的操作是：

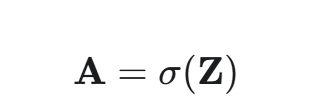
在 NumPy 或 PyTorch 中，这仅仅是一行代码：A = 1 / (1 + np.exp(-Z))。底层会自动并行地计算 Z 中所有元素的指数和除法。

矩阵化 是更高级的向量化，它将对所有样本 和所有特征 的操作统一成一个矩阵运算。这是现代深度学习框架中最常见的形式。

考虑一个包含 m 个样本（x(1),x(2),...,x(m)）的训练批次，每个样本有 n 个特征。我们将所有样本堆叠成一个 特征矩阵 X，其维度为 (n,m) 或 (m,n)，具体取决于约定。

我们还定义一个 权重矩阵 W，其维度取决于网络的结构。假设是全连接层，输入层有 n 个神经元，下一层（隐藏层）有 h 个神经元，则 W 的维度为 (h,n)。

矩阵化运算 (一次性计算整个批次的所有隐藏层激活值):

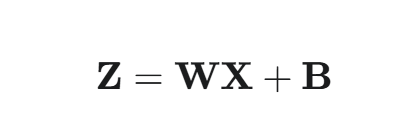
其中：

最终激活值矩阵 A：

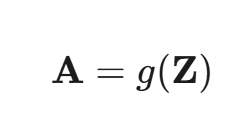
其中 g(⋅) 是激活函数，它以**元素级（element-wise）**的方式作用于矩阵 Z 的每一个元素。A 的维度也是 (h,m)。

在上面的矩阵化公式中，WX 是一个 (h,m) 矩阵，而偏置 b 是一个 (h,1) 向量。要进行加法，它们的维度必须匹配。在深度学习框架（如 NumPy、PyTorch、TensorFlow）中，广播（Broadcasting）机制允许维度不完全匹配的张量进行算术运算。

广播的原理： 当一个较小的张量与一个较大的张量进行运算时，如果它们的维度满足一定条件，较小的张量会被自动复制或扩展，使其形状与较大张量兼容。

在 Z=WX+b 的例子中，(h,1) 的 b 向量会被复制 m 次，沿着其唯一的维度（即 m 轴）扩展为一个 (h,m) 的矩阵 B，从而实现加法。

核心意义： 广播机制极大地简化了代码，避免了手动创建重复的矩阵。开发者只需要关注核心的数学向量/矩阵，而无需编写额外的代码来处理维度匹配。

现代深度学习框架如 PyTorch 和 TensorFlow 本质上就是高度优化的**张量（Tensor）**计算库。

张量（Tensor）： 向量（一维张量）和矩阵（二维张量）的高维推广。深度学习中的数据（如图像、视频、文本序列）都是以高维张量的形式表示。
计算图： 这些框架在底层构建了计算图 ，并使用高度优化的线性代数库 （如 Intel MKL、NVIDIA cuBLAS、cuDNN）来执行张量操作。
- 当用户编写 C = A @ B（矩阵乘法）时，框架不会在 Python 层面执行循环，而是将这个操作发送给底层的 C/C++ 库。
- 如果是在 GPU 上运行，这些库会将矩阵乘法任务分解成数千个并行的小任务，分发给 GPU 的计算核心同时执行，实现了极致的并行化。

正是这种硬件层面的并行 与软件层面的张量抽象相结合，使得深度学习模型能够在合理的时间内完成训练，即使面对万亿次的浮点运算。

向量化和矩阵化是深度学习的性能基石，其重要性体现在以下三个方面：

性能（Speed）： 充分利用 CPU 的 SIMD 指令集和 GPU 的大规模并行计算能力，将计算速度提升数十倍、数百倍甚至数千倍，使大规模模型的训练成为可能。
代码（Clarity）： 将复杂的数学公式直接转化为简洁的代码，提升了代码的可读性、可维护性 和去 Bug 效率。
标准（Foundation）： 它们是所有现代深度学习框架（如 PyTorch/TensorFlow）的核心设计思想。掌握它们是理解和高效使用这些框架，乃至进行**模型部署（Inference）**优化的前提。

简而言之，在深度学习中，一切皆矩阵 ，一切皆并行 。向量化和矩阵化是将复杂的神经网络数学映射到高效的现代计算机硬件上的唯一有效途径。