其实是论文的全文翻译
摘要
深层神经网络的训练难度更高。本文提出一种残差学习框架(residual learning framework) ,旨在降低远超以往深度的网络训练复杂度。我们将网络层明确重构为学习参考层输入的残差函数(learning residual functions with reference to the layer inputs),而非学习无参考基准的函数。综合实证结果表明,该残差网络更易于优化,且能通过显著增加深度提升模型精度。在 ImageNet 数据集上,我们评估了深度达 152 层的残差网络 ------ 其深度为 VGG 网络 [41] 的 8 倍,而复杂度仍保持更低水平。基于该残差网络的集成模型在 ImageNet 测试集上实现 3.57% 的错误率,这一结果斩获 2015 年 ImageNet 大规模视觉识别挑战赛(ILSVRC 2015)图像分类任务冠军。此外,我们还在 CIFAR-10 数据集上完成了 100 层和 1000 层残差网络的性能分析。
特征表示的深度对诸多视觉识别任务至关重要。仅凭借极深的特征表示能力,我们在 COCO 目标检测数据集上实现了 28% 的相对性能提升。深度残差网络是我们参与 2015 年 ILSVRC 与 COCO 竞赛提交方案的核心基础 ¹,且在 ImageNet 检测、ImageNet 定位、COCO 检测及 COCO 分割任务中均荣获冠军。
1. 引言
深度卷积神经网络 [22, 21] 为图像分类任务带来了一系列突破性进展 [21, 50, 40]。深度网络通过端到端的多层架构,自然地整合了低 / 中 / 高级特征 [50] 与分类器,且特征的 "层级" 可通过堆叠层数(深度)进一步丰富。近期研究证据 [41, 44] 表明,网络深度至关重要 ------ 在极具挑战性的 ImageNet 数据集 [36] 上,当前最优结果 [41, 44, 13, 16] 均采用了 "极深"[41] 模型,其深度范围为 16 层 [41] 至 30 层 [16]。此外,许多非平凡视觉识别任务 [8, 12, 7, 32, 27] 也从极深模型中显著受益。
受深度重要性的驱动,一个关键问题应运而生:构建更优网络是否仅需简单堆叠更多层?这一问题的核心障碍是众所周知的梯度消失 / 爆炸问题 [1, 9]------ 该问题从训练初期就阻碍模型收敛。然而,通过归一化初始化 [23, 9, 37, 13] 和中间归一化层 [16],这一问题已得到大幅缓解,使得数十层的网络能够通过随机梯度下降(SGD)与反向传播 [22] 实现收敛。
当深层网络能够启动收敛后,另一个退化问题逐渐显现:随着网络深度增加,模型精度先达到饱和(这一现象或许并不意外),随后迅速下降。出乎意料的是,这种退化并非由过拟合导致 ------ 正如文献 [11, 42] 所报道并经我们实验充分验证的:在已达到合适深度的模型上继续增加层数,会导致训练误差升高。图 1 展示了这一典型现象。
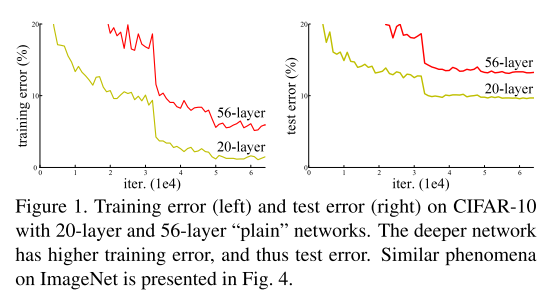
训练精度的退化表明,并非所有网络结构都具备同等的优化易用性。考虑一个较浅的网络架构及其深层扩展版本(在浅层网络基础上添加更多层):对于该深层模型,存在一个构造性最优解 ------ 新增层采用恒等映射(identity mapping),其余层直接复用浅层模型的训练结果。这一构造性解的存在意味着,深层模型的训练误差不应高于其对应的浅层模型。但实验结果显示,我们当前使用的优化器无法找到与该构造性解性能相当或更优的解(或无法在可行时间内找到)。
为解决上述退化问题,本文提出一种深度残差学习框架。我们不再期望每堆叠几层就直接拟合一个期望的底层映射,而是明确让这些层拟合一个残差映射。形式化地,设期望的底层映射为 H (x),我们令堆叠的非线性层拟合另一个映射 F (x) := H (x)−x,此时原映射可重写为 F (x)+x。我们推测,优化残差映射比优化原始的无参考基准映射更为容易。极端情况下,若恒等映射是最优解,则将残差推向零比通过堆叠非线性层拟合恒等映射更简单。
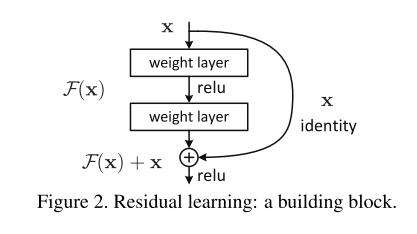
F (x)+x 的形式可通过带有 " shortcut connections(捷径连接)" 的前馈神经网络实现(图 2)。捷径连接 [2, 34, 49] 指跳过一层或多层的连接方式。在本文方法中,捷径连接仅执行恒等映射(identity mapping),其输出与堆叠层的输出相加(图 2)。恒等捷径连接既不引入额外参数,也不增加计算复杂度。整个网络仍可通过随机梯度下降(SGD)与反向传播进行端到端训练,且无需修改优化器,即可利用常用深度学习框架(如 Caffe [19])轻松实现。
我们在 ImageNet 数据集 [36] 上开展了全面实验,以验证退化问题并评估所提方法的性能。实验结果表明:1)我们提出的极深残差网络易于优化,而对应的 "普通网络(plain nets)"(即简单堆叠层的网络)在深度增加时会呈现更高的训练误差;2)深度残差网络能够通过大幅增加深度轻松获得精度提升,其性能显著优于以往网络。
在 CIFAR-10 数据集 [20] 上,我们也观察到了类似现象 ------ 这表明优化难题及本文方法的有效性并非局限于特定数据集。我们在该数据集上成功训练了超过 100 层的模型,并进一步探索了超过 1000 层的网络结构。
在 ImageNet 分类数据集 [36] 上,极深残差网络取得了优异性能:我们的 152 层残差网络是当时 ImageNet 数据集上最深的网络,同时其复杂度仍低于 VGG 网络 [41]。基于该网络的集成模型在 ImageNet 测试集上实现了 3.57% 的 top-5 错误率,并斩获 2015 年 ILSVRC 图像分类竞赛冠军。此外,极深特征表示在其他识别任务中也展现出卓越的泛化能力,助力我们在 2015 年 ILSVRC 与 COCO 竞赛中进一步包揽以下冠军:ImageNet 检测、ImageNet 定位、COCO 检测及 COCO 分割。这一强有力的证据表明,残差学习原理具有通用性,我们期望其可推广至其他视觉及非视觉任务中。
2. 相关工作
残差表示(Residual Representations)
在图像识别领域,VLAD(向量局部聚合描述符)[18] 通过编码相对于字典的残差向量构建特征表示,而 Fisher 向量 [30] 可被表述为 VLAD 的概率版本 [18]。两者均为图像检索与分类任务中性能强大的浅层表示方法 [4, 48]。在向量量化任务中,研究表明 [17],对残差向量进行编码比直接编码原始向量更具有效性。
在低层视觉与计算机图形学领域,为求解偏微分方程(PDEs),广泛应用的多重网格法(Multigrid method)[3] 将系统重构为多尺度下的子问题,每个子问题负责求解粗尺度与细尺度之间的残差解。多重网格法的替代方案是分层基预处理方法 [45, 46],该方法依赖于表示两尺度间残差向量的变量。研究证实 [3, 45, 46],这些求解器的收敛速度远快于未利用解的残差特性的标准求解器。上述方法表明,合理的问题重构或预处理策略能够简化优化过程。
捷径连接(Shortcut Connections)
与捷径连接 [2, 34, 49] 相关的实践与理论研究已开展多年。训练多层感知机(MLPs)的早期实践之一是添加从网络输入直接连接至输出的线性层 [34, 49]。在文献 [44, 24] 中,部分中间层被直接连接至辅助分类器,以缓解梯度消失 / 爆炸问题。文献 [39, 38, 31, 47] 提出了通过捷径连接实现层响应、梯度及传播误差中心化的方法。在文献 [44] 中,"inception 层" 由一个捷径分支和多个更深的分支构成。
与本文工作同期,"高速公路网络(highway networks)"[42, 43] 提出了带有门控函数(gating functions)[15] 的捷径连接。与本文无参数的恒等捷径连接不同,这些门控函数依赖数据且包含可学习参数。当门控捷径 "关闭"(输出趋近于零)时,高速公路网络中的层表示非残差映射;相反,本文的模型架构始终学习残差映射 ------ 恒等捷径连接永不关闭,所有信息始终得以传递,同时模型需学习额外的残差函数。此外,高速公路网络尚未展现出在极深架构(如超过 100 层)下的精度提升能力。
3. 深度残差学习
3.1 残差学习
设 H (x) 为若干堆叠层(不一定是整个网络)需要拟合的底层映射,其中 x 表示该组堆叠层中第一层的输入。若假设多个非线性层能够渐近逼近复杂函数 ²,则等价于假设这些层能够渐近逼近残差函数,即 H (x)−x(假设输入和输出维度相同)。因此,我们不再期望堆叠层直接逼近 H (x),而是明确让这些层逼近残差函数 F (x) := H (x)−x,此时原映射转化为 F (x)+x。尽管两种形式(直接拟合 H (x) 与拟合残差 F (x))理论上均能渐近逼近目标函数(如假设所示),但它们的学习难度可能存在显著差异。
这一重构思路源于退化问题所呈现的反直觉现象(图 1 左图)。如引言所述,若新增层可构造为恒等映射,则深层模型的训练误差应不高于其对应的浅层模型。而退化问题表明,优化器可能难以通过多个非线性层逼近恒等映射。通过残差学习重构后,若恒等映射为最优解,优化器可通过将多个非线性层的权重驱动至零来逼近恒等映射,极大降低学习难度。
在实际场景中,恒等映射未必是最优解,但该重构策略可对优化问题起到预处理作用。若最优函数更接近恒等映射而非零映射,则优化器更易学习相对于恒等映射的微小扰动,而非从零开始学习全新函数。实验结果(图 7)表明,学到的残差函数通常具有较小的响应值,这验证了恒等映射能够提供合理的预处理效果。
3.2 基于捷径连接的恒等映射
我们将残差学习应用于每若干个堆叠层,其基本构建块如图 2 所示。形式化地,本文定义基本构建块为:
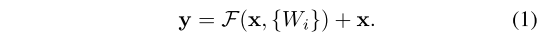
其中,x 和 y 分别为该组堆叠层的输入和输出向量;F (x, {W_i}) 表示待学习的残差映射。以图 2 中包含两层的构建块为例,F 可表示为F=W2σ(W1x)(其中 σ 表示 ReLU 激活函数 [29],为简化符号省略偏置项)。F 与 x 的加法运算通过捷径连接和逐元素加法实现,且在加法运算后引入第二次非线性变换(即 σ(y),见图 2)。
式 (1) 中的捷径连接既不引入额外参数,也不增加计算复杂度 ------ 这不仅在实际应用中具有吸引力,更在普通网络与残差网络的对比实验中至关重要:我们可在参数数量、深度、宽度和计算成本完全一致的前提下(仅忽略不计的逐元素加法除外),对普通网络与残差网络进行公平对比。
式 (1) 要求 x 和 F 的维度必须一致。若维度不匹配(例如改变输入 / 输出通道数),可通过捷径连接引入线性投影Ws以匹配维度:
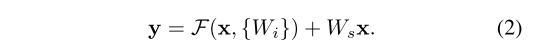
也可在式 (1) 中直接使用方阵Ws,但实验表明,恒等映射已足以解决退化问题且更具经济性,因此Ws仅在维度匹配时使用。
残差函数 F 的形式具有灵活性:本文实验中 F 包含两层或三层(图 5),但也可扩展至更多层。需注意的是,若 F 仅含单层,则式 (1) 退化为类似线性层的结构(y=W1x+x),此时未观察到性能优势。此外,尽管上述符号为简化表述基于全连接层,但该框架同样适用于卷积层:F (x, {W_i}) 可表示多个卷积层,逐元素加法则在两个特征图之间按通道维度执行。
3.3 网络架构
我们测试了多种普通网络与残差网络,观察到一致的实验现象。为提供具体讨论案例,以下描述两种面向 ImageNet 数据集的模型架构:
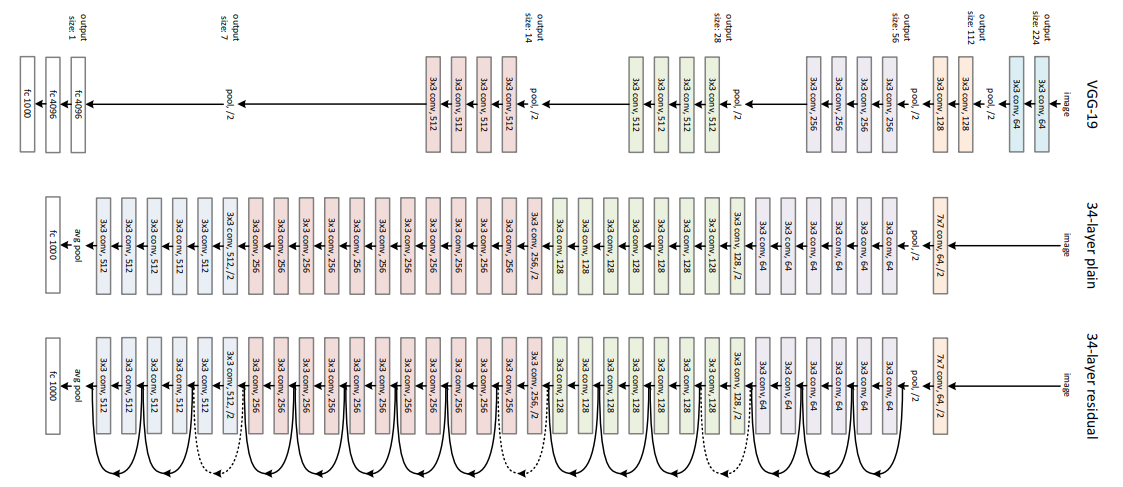
普通网络(Plain Network)
我们的普通网络基线模型(图 3 中间)主要受 VGG 网络 [41] 设计理念启发(图 3 左侧)。卷积层大多采用 3×3 滤波器,并遵循两条简单设计规则:(i)对于输出特征图尺寸相同的层,设置相同数量的滤波器;(ii)若特征图尺寸减半,则滤波器数量加倍,以保持每层的时间复杂度不变。通过步长为 2 的卷积层直接实现下采样操作。网络末尾包含一个全局平均池化层和一个 1000 类全连接层(配 softmax 激活函数)。图 3 中间所示的普通网络共包含 34 个加权层。
值得注意的是,我们的普通网络模型比 VGG 网络 [41](图 3 左侧)具有更少的滤波器数量和更低的复杂度:34 层基线模型的计算量为 36 亿次浮点运算(FLOPs,乘法 - 加法操作),仅为 VGG-19 网络(196 亿次 FLOPs)的 18%。
残差网络(Residual Network)
在上述普通网络基础上,通过插入捷径连接(图 3 右侧),将其转化为对应的残差网络版本。当输入与输出维度一致时(图 3 中实线捷径连接),可直接使用恒等捷径连接(式 (1));当维度增加时(图 3 中虚线捷径连接),考虑两种实现方案:(A)捷径连接仍执行恒等映射,通过填充额外零元素以匹配新增维度,该方案不引入额外参数;(B)采用式 (2) 中的投影捷径连接(通过 1×1 卷积实现)匹配维度。对于两种方案,当捷径连接跨越两种不同尺寸的特征图时,均采用步长为 2 的操作。
3.4 实现细节
ImageNet 数据集上的实现遵循文献 [21, 41] 中的标准流程:
- 数据增强:为实现尺度增强 [41],将图像短边随机采样至 [256, 480] 区间后调整尺寸;从原始图像或其水平翻转结果中随机裁剪 224×224 大小的区域,并减去像素均值 [21];采用文献 [21] 中的标准颜色增强策略。
- 网络训练配置:每个卷积层后、激活函数前引入批量归一化(BN)[16],遵循文献 [16] 的实现方式;权重初始化采用文献 [13] 的方法,所有普通网络与残差网络均从零开始训练;优化器采用随机梯度下降(SGD),批量大小(mini-batch size)设为 256;初始学习率为 0.1,当验证误差趋于平稳时将学习率除以 10,训练迭代次数最高达 6×10⁴次;权重衰减(weight decay)设为 0.0001,动量(momentum)设为 0.9;未使用 dropout [14],与文献 [16] 的实现一致。
- 测试策略:对比实验采用标准 10 裁剪测试(10-crop testing)[21];为获取最优性能,采用文献 [41, 13] 中的全卷积形式,对多个尺度(图像短边分别设为 {224, 256, 384, 480, 640})下的预测分数进行平均。
4. 实验
4.1 ImageNet 分类任务
我们在 ImageNet 2012 分类数据集 [36] 上评估所提方法,该数据集包含 1000 个类别。模型在 128 万张训练图像上进行训练,在 5 万张验证图像上进行性能评估,并通过测试服务器获取 10 万张测试图像的最终结果。评估指标包括 top-1 错误率和 top-5 错误率。
普通网络(Plain Networks)
首先评估 18 层和 34 层普通网络:34 层普通网络结构如图 3(中间)所示,18 层普通网络采用相似架构设计,详细结构参数见表 1。
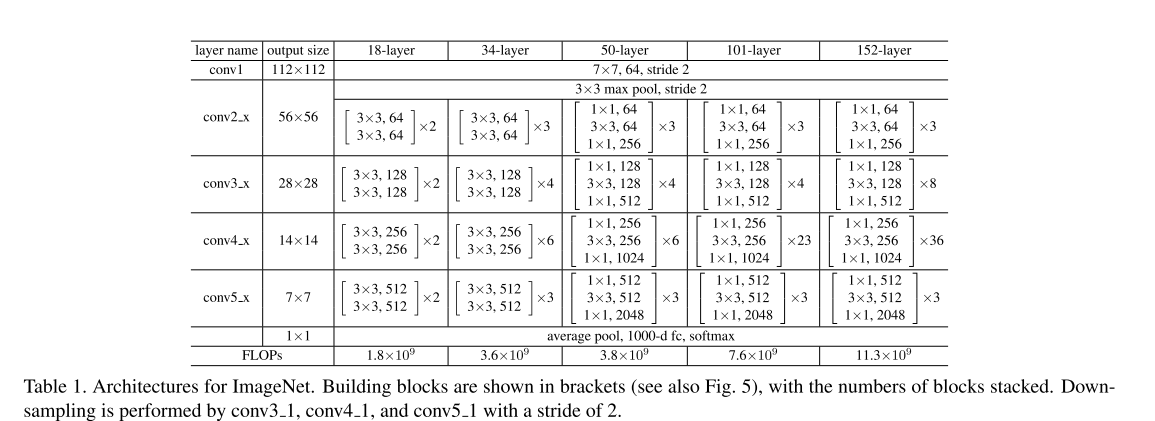
表 2 结果显示,34 层普通网络的验证错误率高于 18 层普通网络。为探究原因,图 4(左图)对比了两者训练过程中的训练 / 验证错误率变化趋势 ------ 我们观察到明显的退化现象:尽管 18 层普通网络的解空间是 34 层网络解空间的子集,但 34 层普通网络在整个训练过程中的训练错误率始终更高。
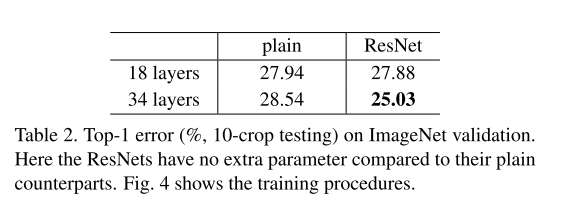
我们认为,这种优化困难并非由梯度消失导致。这些普通网络均采用批量归一化(BN)[16] 训练,该技术可确保前向传播信号保持非零方差;同时我们验证了,BN 的引入使反向传播梯度的范数处于健康范围,因此前向和反向信号均不会消失。事实上,34 层普通网络仍能达到具有竞争力的精度(表 3),表明优化器在一定程度上有效。我们推测,深层普通网络可能存在指数级降低的收敛速率,这一特性影响了训练错误率的下降 ³,其具体原因将在未来研究中进一步探究。
残差网络(Residual Networks)
接下来评估 18 层和 34 层残差网络(ResNets)。基线架构与上述普通网络完全一致,仅在每对 3×3 滤波器后添加捷径连接(如图 3(右侧)所示)。首次对比实验中(表 2、图 4 右图),所有捷径连接均采用恒等映射,维度增加时采用零填充策略(方案 A),因此与对应的普通网络相比无额外参数。
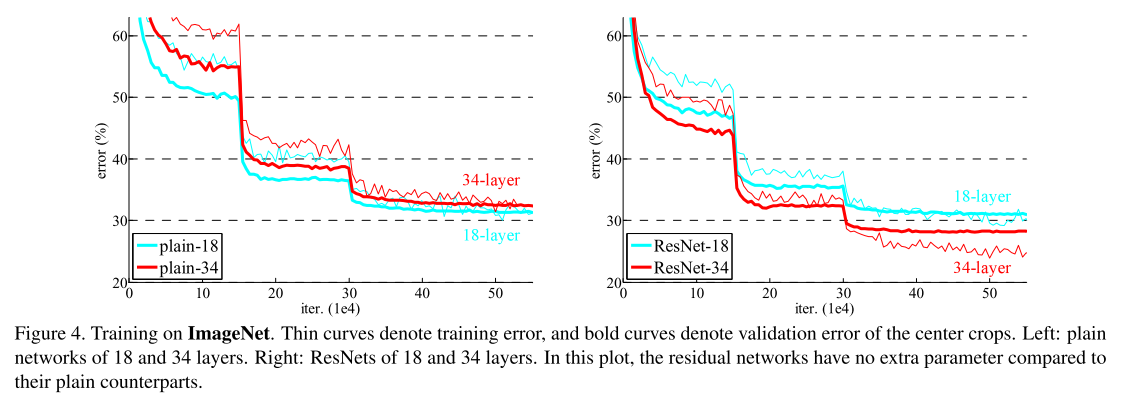
从表 2 和图 4 中可得出三项核心结论:
- 残差学习逆转了深度对性能的影响 ------34 层残差网络性能优于 18 层残差网络(提升 2.8%)。更重要的是,34 层残差网络的训练错误率显著降低,且在验证集上表现出良好的泛化能力,表明该设置下退化问题得到有效解决,模型能够通过增加深度获得精度提升。
- 与对应的 34 层普通网络相比,残差网络的 top-1 错误率降低 3.5%(表 2),这一提升源于训练错误率的成功下降(图 4 右图 vs 左图),验证了残差学习在极深网络中的有效性。
- 18 层普通网络与残差网络的精度相当(表 2),但残差网络的收敛速度更快(图 4 右图 vs 左图)。当网络 "未过度加深" 时(本文中为 18 层),现有 SGD 优化器仍能为普通网络找到较优解,而残差网络通过加速早期训练收敛,进一步降低了优化难度。
恒等捷径连接与投影捷径连接对比(Identity vs. Projection Shortcuts)
前文已验证无参数的恒等捷径连接可有效辅助训练,本节进一步探究投影捷径连接(式 (2))的性能。表 3 对比了三种实现方案:
- 方案 A:维度增加时采用零填充捷径连接,所有捷径连接均无参数(与表 2、图 4 右图设置一致);
- 方案 B:维度增加时采用投影捷径连接,其余场景采用恒等捷径连接;
- 方案 C:所有捷径连接均采用投影操作。
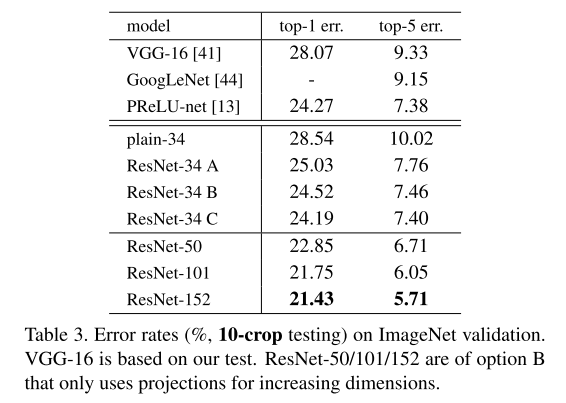
表 3 结果显示,三种方案的性能均显著优于对应的普通网络:方案 B 略优于方案 A,我们认为这是因为方案 A 中零填充的维度未参与残差学习;方案 C 比方案 B 边际性更优,这一提升源于 13 个投影捷径连接引入的额外参数。但 A、B、C 三者间的性能差异较小,表明投影捷径连接并非解决退化问题的核心要素。因此,为降低内存 / 时间复杂度及模型规模,本文后续实验未采用方案 C。恒等捷径连接对于下文将介绍的瓶颈架构尤为重要 ------ 可避免其复杂度增加。
更深的瓶颈架构(Deeper Bottleneck Architectures)
为构建面向 ImageNet 的更深层网络,同时考虑训练时间成本,我们将基本构建块改进为瓶颈设计⁴。对于每个残差函数 F,采用 3 层堆叠结构替代原有的 2 层(图 5):三层卷积分别为 1×1、3×3 和 1×1,其中 1×1 卷积层负责维度缩减与恢复(还原),使中间的 3×3 卷积层成为输入 / 输出维度更小的瓶颈层。图 5 展示了该设计示例,两种架构(2 层原始块与 3 层瓶颈块)的时间复杂度相近。
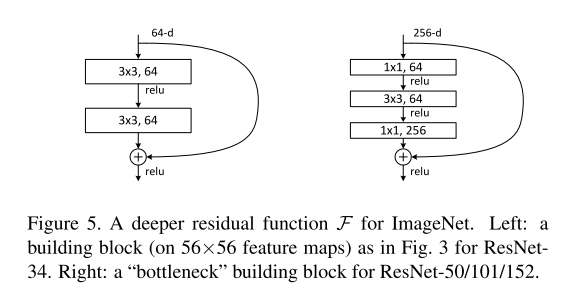
无参数的恒等捷径连接对瓶颈架构至关重要:若将图 5(右侧)中的恒等捷径连接替换为投影连接,由于捷径连接需连接两个高维端点,会导致时间复杂度与模型规模翻倍,因此恒等捷径连接使瓶颈设计的模型更具效率优势。
- 50 层残差网络(50-layer ResNet):将 34 层网络中的每个 2 层块替换为上述 3 层瓶颈块,得到 50 层残差网络(表 1)。维度增加时采用方案 B,该模型的计算量为 38 亿次 FLOPs。
- 101 层与 152 层残差网络(101-layer and 152-layer ResNets):通过堆叠更多 3 层瓶颈块构建 101 层和 152 层残差网络(表 1)。值得注意的是,尽管深度显著增加,152 层残差网络(113 亿次 FLOPs)的复杂度仍低于 VGG-16/19 网络(分别为 153 亿 / 196 亿次 FLOPs)。
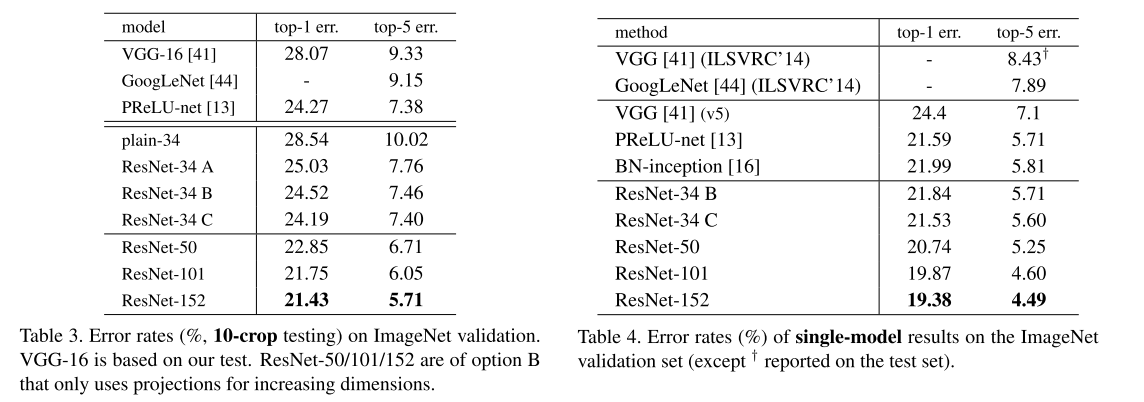
实验结果表明,50/101/152 层残差网络的精度较 34 层网络有显著提升(表 3、表 4),且未观察到退化现象 ------ 这证实模型可通过大幅增加深度获得显著精度增益,且该深度优势在所有评估指标中均有体现(表 3、表 4)。
与现有最优方法对比(Comparisons with State-of-the-art Methods)
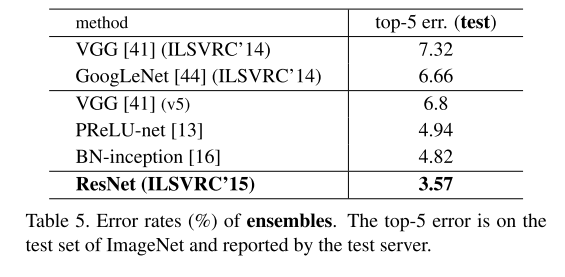
表 4 对比了本文方法与此前最优单模型结果:34 层残差网络基线模型已达到极具竞争力的精度;152 层残差网络的单模型 top-5 验证错误率低至 4.49%,这一结果优于此前所有集成模型的性能(表 5)。我们将 6 个不同深度的模型组合为集成模型(提交时仅包含 2 个 152 层模型),在测试集上实现 3.57% 的 top-5 错误率(表 5),该结果斩获 2015 年 ILSVRC 竞赛冠军。
4.2 CIFAR-10 数据集实验与分析
我们在 CIFAR-10 数据集 [20] 上开展了进一步研究,该数据集包含 10 个类别,共 5 万张训练图像和 1 万张测试图像。实验基于训练集训练模型并在测试集上评估性能,研究重点为极深网络的行为特性,而非追求现有最优结果,因此特意采用如下简洁架构设计:
普通网络与残差网络的架构遵循图 3(中间 / 右侧)的设计形式:
- 输入为 32×32 图像,训练前减去像素均值;
- 第一层为 3×3 卷积层;
- 后续堆叠 6n 层 3×3 卷积层,分别作用于尺寸为 {32, 16, 8} 的特征图(每种尺寸对应 2n 层),滤波器数量分别为 {16, 32, 64};
- 通过步长为 2 的卷积层实现下采样;
- 网络末尾包含全局平均池化层、10 类全连接层及 softmax 激活函数。
网络总加权堆叠层数为 6n+2,架构总结如下:
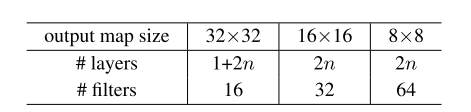
采用捷径连接时,所有连接均作用于每对 3×3 层(共 3n 个捷径连接)。本数据集实验中,所有场景均采用恒等捷径连接(即方案 A),因此残差模型与对应的普通网络在深度、宽度和参数数量上完全一致。
实验配置
- 训练参数:权重衰减设为 0.0001,动量为 0.9;采用文献 [13] 的权重初始化方法与批量归一化(BN)[16],未使用 dropout;
- 训练设备与批量大小:在两块 GPU 上训练,批量大小(mini-batch size)为 128;
- 学习率调度:初始学习率为 0.1,分别在 3.2 万次和 4.8 万次迭代时除以 10,6.4 万次迭代时终止训练(该调度策略基于 4.5 万 / 0.5 万的训练 / 验证集划分确定);
- 数据增强:训练阶段采用文献 [24] 的简洁增强策略 ------ 图像四周填充 4 个像素,从填充后的图像或其水平翻转结果中随机裁剪 32×32 区域;
- 测试策略:仅对原始 32×32 图像的单视角进行评估。
实验结果与分析
我们对比了 n={3,5,7,9} 对应的 20 层、32 层、44 层和 56 层网络:
- 普通网络行为(图 6 左图):深层普通网络受深度增加的负面影响,随着层数加深,训练误差显著升高。这一现象与 ImageNet 数据集(图 4 左图)及 MNIST 数据集(见文献 [42])的结果一致,表明该优化困难是一个基础性问题。
- 残差网络行为(图 6 中图):与 ImageNet 实验结果(图 4 右图)类似,残差网络成功克服了优化困难,随着深度增加实现精度提升。
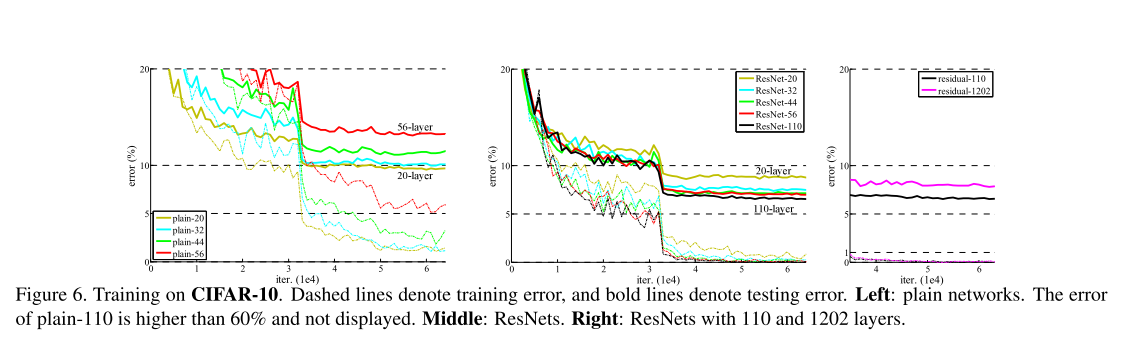
我们进一步探索了 n=18 对应的 110 层残差网络:
- 训练调整:初始学习率 0.1 略大,导致模型难以启动收敛⁵。因此采用 0.01 的学习率热身训练,直至训练误差低于 80%(约 400 次迭代),随后恢复为 0.1 继续训练,其余学习调度策略保持不变;
- 性能表现:110 层网络收敛效果良好(图 6 中图),其参数数量少于 FitNet [35]、Highway [42] 等其他深层窄网络(表 6),但仍达到现有最优水平(测试错误率 6.43%,表 6)。

层响应分析(Analysis of Layer Responses)
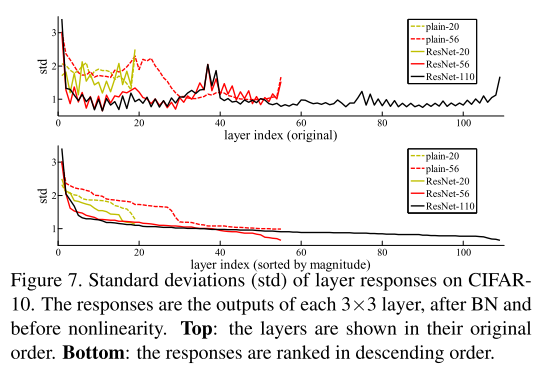
图 7 展示了层响应的标准差(std)------ 响应指每个 3×3 层的输出(经过 BN 处理后、其他非线性变换(ReLU / 加法)前的结果)。对残差网络而言,该分析反映了残差函数的响应强度:
- 残差网络的层响应普遍小于对应的普通网络,支持本文核心假设(3.1 节):残差函数通常比非残差函数更接近零;
- 深层残差网络的响应幅度更小(图 7 中 ResNet-20、56、110 的对比),表明随着层数增加,残差网络中单个层对信号的修改幅度趋于减小。
千层以上网络探索(Exploring Over 1000 Layers)
我们构建了超深的 1202 层网络(n=200),采用上述训练策略训练:
- 优化表现:模型无明显优化困难,训练误差低于 0.1%(图 6 右图);
- 测试性能:测试错误率仍保持较好水平(7.93%,表 6);
- 现存问题:尽管 1202 层网络与 110 层网络的训练误差相近,但其测试误差更高,推测原因是过拟合 ------ 对于 CIFAR-10 这种小型数据集,1202 层网络(1940 万参数)可能过于庞大。现有该数据集的最优结果 [10,25,24,35] 均采用了 maxout [10] 或 dropout [14] 等强正则化方法;
- 未来方向:本文为聚焦优化困难问题,未使用 maxout/dropout,仅通过 "深层窄架构" 设计施加简洁正则化。后续研究可结合强正则化进一步提升超深网络在小型数据集上的泛化性能。
4.3 PASCAL与PASCAL上的目标检测任务

我们的方法在其他识别任务中展现出了良好的泛化性能。表 7 和表 8 呈现了该方法在帕斯卡视觉目标分类挑战赛 2007 年与 2012 年数据集以及微软通用目标数据集上的目标检测基准测试结果。我们采用快速区域卷积神经网络作为检测方法,本部分重点研究将骨干网络由视觉几何组网络 16 层版本替换为残差网络 101 层版本后检测效果的提升情况。两种模型的检测实现流程完全一致,因此检测性能的提升可完全归功于残差网络这一更优的网络结构。值得关注的是,在具有挑战性的微软通用目标数据集上,该方法使该数据集的标准评价指标(多尺度平均精度)提升了 6.0%,相对提升幅度达 28%。这一性能提升完全得益于残差网络学到的高质量特征表示。依托深度残差网络,我们在 2015 年大规模视觉识别挑战赛与微软通用目标检测竞赛中的多个项目中均斩获冠军,包括 ImageNet 图像检测任务、ImageNet 图像定位任务、微软通用目标检测任务以及微软通用目标分割任务,具体细节详见附录内容。