【视觉SLAM十四讲】视觉里程计 1

文章目录

- 特征点匹配
- - [ORB 特征](#ORB 特征)
  - - [FAST 关键点](#FAST 关键点)
  - [BRIEF 描述子](#BRIEF 描述子)
  - [ORB 的改进](#ORB 的改进)
  - - 尺度不变性
    - 旋转不变性
  - 特征匹配
- 2D-2D：对极几何
- - 本质矩阵
  - - [多于 8 对点的情况](#多于 8 对点的情况)
  - 单应矩阵
  - 三角测量
- 3D-2D：PnP
- 3D-3D：ICP
- - [SVD 法求解](#SVD 法求解)
  - [SVD 法代码实现](#SVD 法代码实现)

特征点匹配

视觉里程计的核心问题是根据图像估计相机运动，而这通常通过帧间的图像变化实现。为了简化运算，我们会从图像中选取特征点，这些点在相机视角发生较小变化时仍然存在，通过特征点在图像上的变化，估计相机位姿的改变。

特征点由关键点 和描述子两部分组成。前者指的是特征点在图像中的位置，后者则指该关键点周围像素的信息，这里讲讲比较有代表性的 ORB 特征

ORB 特征

FAST 关键点

FAST 算法的思路为：如果一个像素与周围邻域的像素差别过大时，就认为其为一个角点。由于仅仅需要比较像素之间的灰度值大小，计算量要小得多

其实现步骤如下：

在图像中选取一像素 p p p ，假设其亮度为 I P I_P IP
设定一个合适的阈值 T T T
选取以 p p p 为中心，半径为 3 的圆上的 16 个像素点
如果选取的像素点存在连续的 N 个点的亮度大于 I P + T I_P+T IP+T 或者小于 I P − T I_P-T IP−T ，那么该点可视为一个角点（ N N N 通常取12）

对于 FAST-12 算法，还有个预测试操作：直接检测邻域圆上的第 1，5，9，13 的像素点亮度，只有至少其中 3 个亮度大于 I P + T I_P+T IP+T 或者小于 I P − T I_P-T IP−T ，才有可能是一个角点

BRIEF 描述子

在提取到关键点之后，我们要对每个点计算其描述子。BRIEF 描述子是一种二进制描述子。在特征点周围选取 256 对随机像素 p , q p,q p,q ，如果 I P > I q I_P > I_q IP>Iq ，则即为 1，反之则即为 0

BRIEF 描述子之间的相似性通常用汉明距离来体现，即两个描述子按位比较，不相同的位数有多少，汉明距离就是多少

ORB 的改进

FAST 和 BRIEF 主要有两个缺点：

不具有尺度不变性：同一目标在图像中可能因拍摄距离不同而呈现不同大小，可能被误判为其他物体
不具有旋转不变性：同上，同一目标的不同旋转状态可能被误判为其他物体

尺度不变性

ORB 采用的是图像金字塔，即以原始图像为第 0 层，进行多次降采样（缩小）生成一系列不同分辨率的图像，这样就可以在进行特征匹配时达到尺度不变性的效果

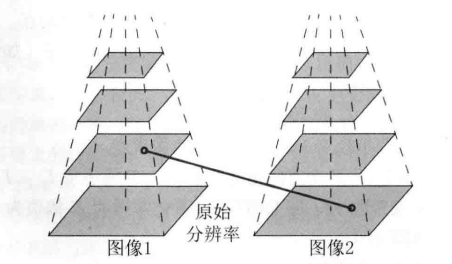
举个例子，我们在当前帧（frame 1）找到了一个特征点，此时相机向前移动靠近该特征点，使其在图像（frame 2）上占比变大。我们从 frame 2 图像金字塔的顶层开始搜索找到特征点的大致位置，然后将预测结果放大相应的倍数传递到下一层，如此反复直至在某一次获得了精确的匹配位置

旋转不变性

ORB 采用的是灰度质心法，其核心思想是为特征点计算出一个"主方向"，后续生成描述子时，会先将图像块旋转到该主方向后再进行计算

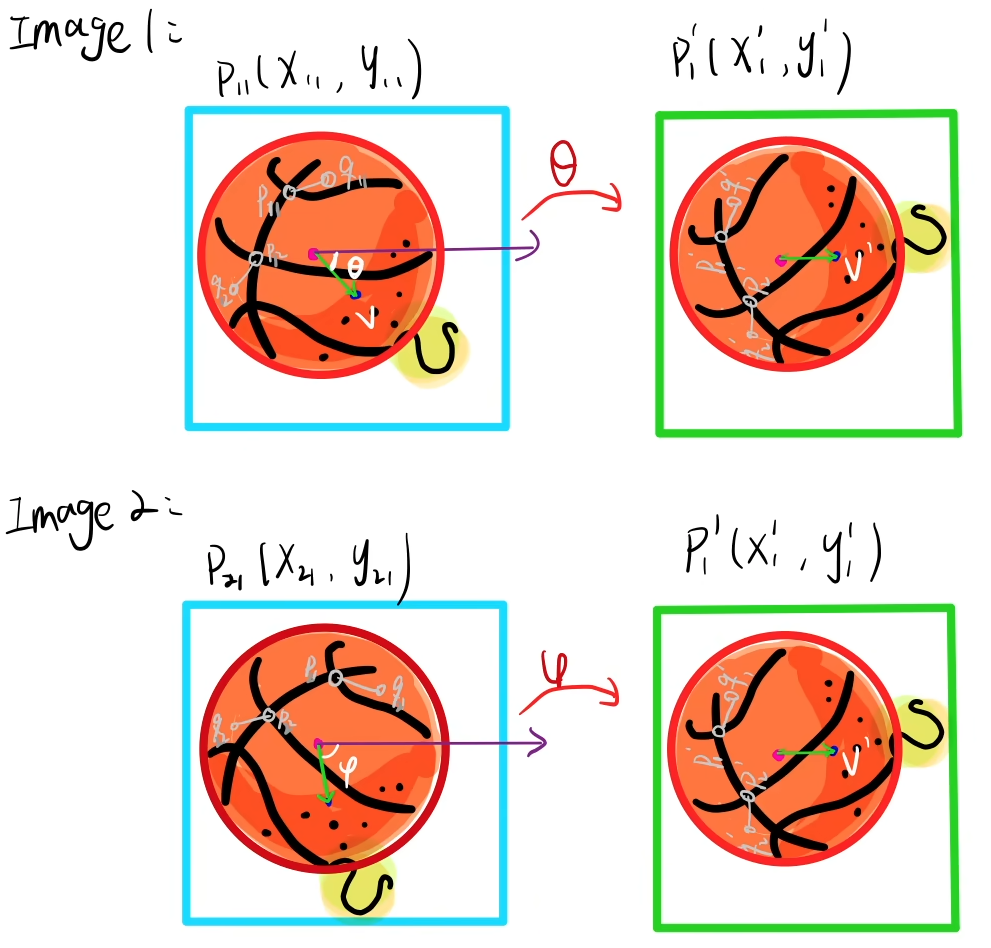
假设我们有一大小为 N × N N\times N N×N 的图像块 A A A ，其几何中心为 C C C

计算零阶距（ m 00 m_{00} m00）和一阶距（ m 10 , m 01 m_{10},m_{01} m10,m01）：灰度值加权的坐标和，即"质量"分布中心
m p q = ∑ x , y ∈ B x p y q I ( x , y ) p , q = 0 , 1 m_{pq}=\sum_{x,y\in B}x^py^qI(x,y)\quad p,q={0,1} mpq=∑x,y∈BxpyqI(x,y)p,q=0,1
计算质心： C = ( m 10 m 00 , m 01 m 00 ) C=\left( \frac{m_{10}}{m_{00}},\frac{m_{01}}{m_{00}} \right) C=(m00m10,m00m01)
连接几何中心 O O O 和质心 C C C ，得到一方向向量 O C → \overrightarrow {OC} OC ，于是特征点的方向可定义为
θ = arctan ⁡ ( m 01 m 10 ) \theta = \arctan \left(\frac{m_{01}}{m_{10}}\right) θ=arctan(m10m01)

下面是一份灰度质心法的使用和描述子计算的大致代码：

cpp 复制代码

void computeORB(const cv::Mat img, std::vector<cv::KeyPoint> &keyPoints, std::vector<DescType> &descriptors)
{
    const int half_patch_size = 8;               // 用于计算方向的图像块大小
    const int half_boundary = 16;                // 定义图像边界缓冲区
    for (auto &kp : keyPoints)
    {
        // 除去边界上的点
        if (kp.pt.x < half_boundary || kp.pt.y < half_boundary || kp.pt.x >= img.cols - half_boundary || kp.pt.y >= img.rows - half_boundary)
        {
            descriptors.push_back({});
            continue;
        }
        
        // 计算一阶矩
        float m10 = 0, m01 = 0;
        for (int dx = -half_patch_size; dx < half_patch_size; dx++)
        {
            for (int dy = -half_patch_size; dy < half_patch_size; dy++)
            {
                // 获取当前像素值
                uchar pixel = img.at<uchar>(kp.pt.y + dy, kp.pt.x + dx);
                m10 += dx * pixel;
                m01 += dy * pixel;
            }
        }

        // 计算特征点方向
        float m_sqrt = sqrt(m10 * m10 + m01 * m01);
        float sin_theta = m01 / m_sqrt;
        float cos_theta = m10 / m_sqrt;

        DescType desc(8, 0);
        for (int i = 0; i < 8; i++)
        {
            uint32_t d = 0;
            for (int j = 0; j < 32; j++)
            {
                int idx_pq = i * 8 + j;
                cv::Point2f p(ORB_pattern[idx_pq * 4], ORB_pattern[idx_pq * 4 + 1]);
                cv::Point2f q(ORB_pattern[idx_pq * 4 + 2], ORB_pattern[idx_pq * 4 + 3]);

                // 计算旋转后的坐标
                cv::Point2f p_rot = cv::Point2f(p.x * cos_theta - p.y * sin_theta, p.x * sin_theta + p.y * cos_theta) + kp.pt;
                cv::Point2f q_rot = cv::Point2f(q.x * cos_theta - q.y * sin_theta, q.x * sin_theta + q.y * cos_theta) + kp.pt;

                if (img.at<uchar>(p_rot.y, p_rot.x) < img.at<uchar>(q_rot.y, q_rot.x))
                {
                    // 通过位运算 i << j，利用一个32位的整数存储32个二进制结果
                    d |= 1 << j;
                }
            }
            desc[i] = d;
        }
        descriptors.push_back(desc);
    }
}

特征匹配

通过上面的步骤，我们现在得到两帧图像各自的特征点，那么我们该怎么找到他们之间的对应关系呢？

暴力匹配：对于两张图片的描述子集，一一计算汉明距离以找到对应的匹配点。实现简单，计算精确；但计算量大，仅适合特征点少的情况
快速近似最近邻(FLANN)：在匹配前，FLANN 会先用其中一张图像的描述子集构建一个数据索引结构，这一步比较耗时但仅需进行一次，对于另一张图像的每一个描述子，在这个预先构建的索引结构上快速搜索找到近似的几个目标，最后利用最近邻距离和次近邻距离的比值筛选匹配结果。对于大规模的特征匹配速度几块，但结果相对并不精确，而且构建索引比较耗时，在较小特征点时使用可能得不偿失

2D-2D：对极几何

对于已匹配到特征点的相邻帧，可建立如下模型

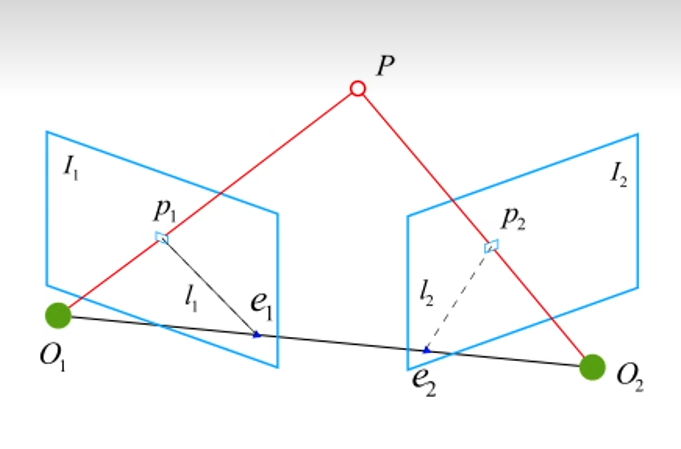
此时存在对极约束
x 2 T t ∧ R x 1 = p 2 T K − T t ∧ R K − 1 p 1 = 0 ( x 是 p 在归一化平面上的像素坐标 ) x_2^Tt^\wedge Rx_1 =p_2^TK^{-T}t^\wedge RK^{-1}p_1=0\quad(x是p在归一化平面上的像素坐标) x2Tt∧Rx1=p2TK−Tt∧RK−1p1=0(x是p在归一化平面上的像素坐标)

其中，我们通常定义基础矩阵 E = t ∧ R , 本质矩阵 F = K − T E K − 1 \text{基础矩阵}~E=t^\wedge R,\quad \text{本质矩阵}~F=K^{-T}EK^{-1} 基础矩阵 E=t∧R,本质矩阵 F=K−TEK−1

可以进一步简化对极约束： x 2 T E x 1 = p 2 T F p 1 = 0 x_2^TEx_1=p_2^TFp_1=0 x2TEx1=p2TFp1=0

本质矩阵

本质矩阵 E E E 是一个 3 × 3 3\times3 3×3 矩阵

对 E E E ，乘以任意一个非零常数，对极约束仍然满足，故可认为 E E E 在不同尺度下是等价的
本质矩阵的奇异值必定是 $σ , σ , 0$ T ( σ > 0 ) $\\sigma,\\sigma,0$ ^T(\sigma>0) $σ,σ,0$ T(σ>0)
由于平移和旋转各有 3 个自由度，故 t ∧ R t^\wedge R t∧R 共有 6 个自由度，由于尺度等价性，故 E E E 实际有 5 个自由度

通常使用八点法 来线性求解 E E E ，八点法利用 8 对匹配点构建线性方程组，通过 SVD 求解 E E E

对于一对匹配点，其归一化坐标为 x 1 = $u 1 , v 1 , 1$ , x 2 $u 2 , v 2 , 1$ x_1= $u_1,v_1,1$ ,~~x_2 $u_2,v_2,1$ x1= $u1,v1,1$ , x2 $u2,v2,1$
( u 2 , v 2 , 1 ) ( e 1 e 2 e 3 e 4 e 5 e 6 e 7 e 8 e 9 ) ( u 1 u 2 u 3 ) = 0 \left( u_2,v_2,1 \right)\begin{pmatrix} e_1 & e_2 & e_3 \\ e_4 & e_5 & e_6 \\ e_7 & e_8 & e_9 \end{pmatrix}\begin{pmatrix} u_1 \\ u_2 \\ u_3 \end{pmatrix} = 0 (u2,v2,1) e1e4e7e2e5e8e3e6e9 u1u2u3 =0

将 e e e 转化为列向量，写成与 e e e 有关的线性形式
$u 2 u 1 , u 2 v 1 , u 2 , v 2 u 1 , v 2 v 1 , v 2 , u 1 , v 1 , 1$ ⋅ e = 0 $u_2u_1,u_2v_1,u_2,v_2u_1,v_2v_1,v_2,u_1,v_1,1$ \cdot e=0 $u2u1,u2v1,u2,v2u1,v2v1,v2,u1,v1,1$ ⋅e=0

以此类推我们就得到了八个线性方程，如果这八对点都不共面（系数矩阵满秩），则可得到唯一解

对于估得的本质矩阵 E E E ，现在的任务是从中恢复出 R , t R,t R,t 。对 E E E 进行奇异值分解（SVD）
E = U Σ V T E=U\Sigma V^T E=UΣVT

我们会得到 4 个可能的 ( R , t ) (R,t) (R,t) 解：
t 1 = U ( : , 3 ) , t 2 = − U ( : , 3 ) R 1 = U R z ( π 2 ) V T , R 2 = U R Z ( − π 2 ) V T t_1=U(:,3),\quad t_2=-U(:,3) \\ R_1=UR_z(\frac{\pi}{2})V^T, \quad R_2=UR_Z(-\frac{\pi}{2})V^T t1=U(:,3),t2=−U(:,3)R1=URz(2π)VT,R2=URZ(−2π)VT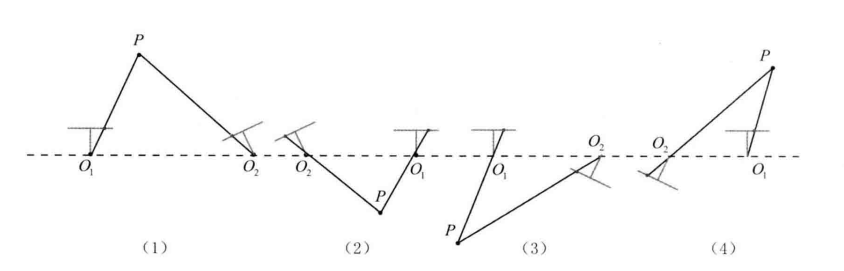

只有正确解能够在两个相机中都拥有正的深度，只要检测点在两个相机下的深度就可筛选出正确解

多于 8 对点的情况

当匹配对数超过 8 对时，八点法可能构成超定方程无法求解，需要采取其他方法

最小二乘法：
- 设系数矩阵为 A A A ，此时有 A e = 0 Ae=0 Ae=0
  min ⁡ e ∣ ∣ A e ∣ ∣ 2 2 = min ⁡ e ∣ ∣ U Σ V T e ∣ ∣ 2 \underset{e}{\min}||Ae||_2^2=\underset{e}{\min}||U\Sigma V^Te||^2 emin∣∣Ae∣∣22=emin∣∣UΣVTe∣∣2
- 因为 U U U 是正交矩阵不影响范数且对变量无影响，故舍去。此时设 y = V T e y=V^Te y=VTe ，由于 V V V 是正交矩阵， ∣ y ∣ = ∣ e ∣ = 1 |y|=|e|=1 ∣y∣=∣e∣=1
- 此时问题变为最小化 ∣ Σ y ∣ 2 = ] σ 1 2 y 1 2 + σ 2 2 y 2 2 + ... + σ 9 2 y 9 2 |\Sigma y|^2=]\sigma_1^2y_1^2+\sigma_2^2y_2^2+\ldots+\sigma_9^2y_9^2 ∣Σy∣2=]σ12y12+σ22y22+...+σ92y92
- 由于 σ 1 ≥ σ 2 ≥ ... ≥ σ 9 \sigma_1 \ge \sigma_2 \ge \ldots \ge \sigma_9 σ1≥σ2≥...≥σ9 ，权重必然被分配给 y 9 y_9 y9 ，即令 y = $0 , 0 , ... , 0 , 1$ T y= $0,0,\\ldots,0,1$ ^T y= $0,0,...,0,1$ T 。因此， e = V y = V . , 9 e=Vy=V_{.,9} e=Vy=V.,9
- 将求得的向量 e e e 转换会 3 × 3 3\times3 3×3 的矩阵 E ∗ E^* E∗
- 强制内在约束 ：对 E ∗ E^* E∗ 进行 SVD 分解，将其奇异值矩阵设为 Σ ′ = d i a g ( ( σ 1 + σ 2 ) / 2 , ( σ 1 + σ 2 ) / 2 , 0 ) \Sigma'= diag((\sigma_1+\sigma_2)/2,(\sigma_1+\sigma_2)/2,0) Σ′=diag((σ1+σ2)/2,(σ1+σ2)/2,0) ，再重构得到最终的本质矩阵 E E E
最小二乘法虽然在数学上是最优解，但对误匹配和噪声及其敏感
随机采样一致性：
- 从所有匹配点中随机抽取 8 对，并使用这 8 对点使用八点法求出一个本质矩阵 E i E_i Ei
- 计算所有匹配点在模型 E i E_i Ei 下的误差（即对极约束 x 2 T E i x 1 \mathbf{x}_2^T E_i \mathbf{x}_1 x2TEix1 的值），如果误差小于阈值，则视为该模型的内点
- 重复以上步骤 N 次，最有模型即所有迭代中内点数量最多的那个
随机采样一致性虽然计算时间不确定，但其出色的鲁棒性，使其在实际应用中几乎总是使用

单应矩阵

当场景中的特征点都落在同一平面上（或者相机纯旋转）时，可以通过单应性进行运动估计

设匹配好的特征点 p 1 , p 2 p_1,p_2 p1,p2 ，特征点落在平面 P P P 上，该平面的法向量为 n n n ，原点（第一个相机的光心）到平面的负距离为 d d d
n T P + d = 0 ⇒ − n T P d = 1 n^TP+d=0\quad \Rightarrow \quad -\frac{n^TP}{d}=1 nTP+d=0⇒−dnTP=1

那么：
p 2 ≃ K ( R P + t ) ≃ K ( R P + t ⋅ ( − n T P d ) ) ≃ K ( R − t n T d ) K − 1 p 1 \begin{align*} p_2 &\simeq K(RP+t) \\ &\simeq K\left(RP+t \cdot (-\frac{n^TP}{d})\right) \\ &\simeq K\left(R-\frac{tn^T}{d}\right)K^{-1}p_1 \end{align*} p2≃K(RP+t)≃K(RP+t⋅(−dnTP))≃K(R−dtnT)K−1p1

于是我们得到了 p 1 p_1 p1 和 p 2 p_2 p2 之间的关系： p 2 ≃ H p 1 p_2 \simeq Hp_1 p2≃Hp1

消去尺度因子得到
u 2 = h 1 u 1 + h 2 v 1 + h 3 h 7 u 1 + h 8 v 1 + h 9 v 2 = h 4 u 1 + h 5 v 1 + h 6 h 7 u 1 + h 8 v 1 + h 9 u_2=\frac{h_1u_1+h_2v_1+h_3}{h_7u_1+h_8v_1+h_9} \qquad v_2=\frac{h_4u_1+h_5v_1+h_6}{h_7u_1+h_8v_1+h_9} u2=h7u1+h8v1+h9h1u1+h2v1+h3v2=h7u1+h8v1+h9h4u1+h5v1+h6

固定 h 9 = 1 h_9=1 h9=1 ，可整理得
h 1 u 1 + h 2 v 1 + h 3 − h 7 u 1 u 2 − h 8 v 1 u 2 = u 2 h 4 u 1 + h 5 v 1 + h 6 − h 7 u 1 v 2 − h 8 v 1 v 2 = v 2 h_1u_1+h_2v_1+h_3-h_7u_1u_2-h_8v_1u_2=u_2 \\ h_4u_1+h_5v_1+h_6-h_7u_1v_2-h_8v_1v_2=v_2 h1u1+h2v1+h3−h7u1u2−h8v1u2=u2h4u1+h5v1+h6−h7u1v2−h8v1v2=v2

提取其约束，令
A 1 = ( u 1 1 v 1 1 1 0 0 0 − u 1 1 u 2 1 − v 1 1 u 2 1 0 0 0 u 1 1 v 1 1 1 − i u 1 1 v 2 1 − v 1 1 v 2 1 ) A_1=\begin{pmatrix} u_1^1 & v_1^1 & 1 & 0 & 0 & 0 & -u_1^1u_2^1 & -v_1^1u_2^1 \\ 0 & 0 & 0 & u_1^1 & v_1^1 & 1 & -iu_1^1v_2^1 & -v_1^1v_2^1 \end{pmatrix} A1=(u110v110100u110v1101−u11u21−iu11v21−v11u21−v11v21)

将 4 对匹配点的方程合并，以恢复单应矩阵 H H H ，后面的求解就与本质矩阵 E E E 类似了

三角测量

对于单目 slam ，仅通过单张图像无法获得像素的深度信息，我们需要通过三角测量的方法估计深度

三角测量是已知两个相机之间的相对位姿 ( R , t ) (R,t) (R,t) 和一对匹配点 p 1 p_1 p1 和 p 2 p_2 p2 ，计算该匹配点所对应的三维空间点 P P P 的位置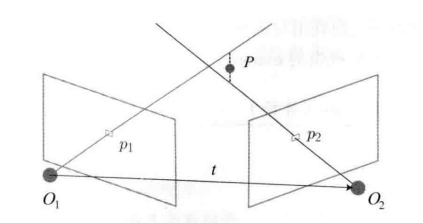

如图， O 1 , O 2 O_1,O_2 O1,O2 是相机光心， p 1 , p 2 p_1,p2 p1,p2 是匹配点。由于噪声的存在，两条射线未必会相交，因此找到一 P P P 点使它到两条射线的距离之和最小就是三角测量的目标
s 1 x 1 = p 1 s 2 x 2 = p 2 = R p 1 + t s_1x_1=p_1\\ s_2x_2=p_2=Rp_1+t s1x1=p1s2x2=p2=Rp1+t

其中 s 1 , s 2 s_1,s_2 s1,s2 是 P P P 点在两个坐标系下的深度值
s 2 x 2 = s 1 R x 1 + t ⇒ s 2 x 2 ∧ x 2 = 0 = s 1 x 2 ∧ R x 1 + x 2 ∧ t s_2x_2=s_1Rx_1+t \quad \Rightarrow \quad s_2x_2^\wedge x_2=0=s_1x_2^\wedge Rx_1+x_2^\wedge t s2x2=s1Rx1+t⇒s2x2∧x2=0=s1x2∧Rx1+x2∧t

于是我们得到了一个关于未知数 s 1 s_1 s1 的线性方程

3D-2D：PnP

当我们得知了场景中一些特征点的 3D 位置，并且又在当前帧观测到了，那么最少只需 3 个点对就可以估计相机运动

直接线性变换（DLT）

将旋转矩阵 R R R 和平移向量 t t t 视为未知的线性变量，直接构建线性方程求解

假设某个空间点 P = ( X , Y , Z , 1 ) T P=(X,Y,Z,1)^T P=(X,Y,Z,1)T ，在图像 I 1 I_1 I1 中投影到点 x 1 = ( u 1 , v 1 , 1 ) T x_1=(u_1,v_1,1)^T x1=(u1,v1,1)T ，此时定义一个包含了旋转和平移信息的增广矩阵 $R ∣ t$ $R\|t$ $R∣t$ （和变换矩阵不同，其并不需要满足任何旋转矩阵的约束），此时我们得到如下展开形式：
s ( u 1 v 1 1 ) = ( t 1 t 2 t 3 t 4 t 5 t 6 t 7 t 8 t 9 t 10 t 11 t 12 ) ( X Y Z 1 ) s\begin{pmatrix}u_1\\v_1\\1\end{pmatrix}=\begin{pmatrix}t_1&t_2&t_3&t_4\\t_5&t_6&t_7&t_8\\t_9&t_{10}&t_{11}&t_{12}\end{pmatrix}\begin{pmatrix}X\\Y\\Z\\1\end{pmatrix} s u1v11 = t1t5t9t2t6t10t3t7t11t4t8t12 XYZ1

这里将旋转矩阵和平移向量看成 12 个未知数，因此最少需要 6 对匹配点来求解。但是通过该方法求得的 R R R 可能并不满足旋转矩阵应有的约束，因此我们需要找到一个最合适的旋转矩阵来对它近似。

P3P

仅需 3 对不共线的 3D-2D 点和一对验证点就能求解位姿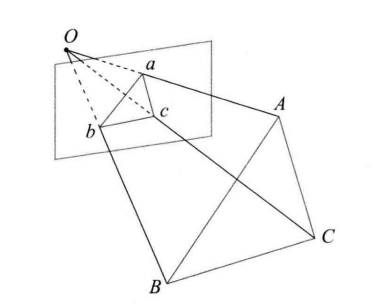

P3P 利用三角形相似，建立如下方程
O A 2 + O B 2 − 2 ⋅ O A ⋅ O B ⋅ cos ⁡ ( ∠ A O B ) = A B 2 OA^2+OB^2-2\cdot OA\cdot OB\cdot\cos(∠AOB)=AB^2 OA2+OB2−2⋅OA⋅OB⋅cos(∠AOB)=AB2

其余两边建立类似方程，我们就可以得到 A , B , C A,B,C A,B,C 在相机坐标系下的 3 D 3D 3D 坐标，最后问题就转换为了一个 3 D − 3 D 3D-3D 3D−3D 问题

P3P 只能利用 3 点的信息，而且受噪声影响严重，只要 3 点共线或者存在误匹配，则算法失效

EPnP

EPnP 适用于任意数量点（ ≥ 4 \ge4 ≥4），其核心思想是将 3D 点表示为四个控制点的加权和，将问题转化为求解控制点在相机坐标系下的坐标

选择世界坐标系下点的质心以及三个主方向上的点
每个 3D 点都可以表示为四个控制点的加权和
P i ω = ∑ j = 1 4 a i j c j ω P_i^{\omega}=\sum_{j=1}^4a_{ij}c_j^\omega Piω=j=1∑4aijcjω
将控制点在相机坐标系下的坐标代入投影方程建立线性方程组
通过 SVD 求解控制点下的坐标代入相机坐标系下的坐标，并利用控制点在世界坐标和空间坐标系下的坐标，通过 3 D − 3 D 3D-3D 3D−3D 方法来求解

EPnP 因为稳定高效，是最常用的 P n P PnP PnP 方法之一（OpenCV 的 slovePnP 就是 EPnP）

最小重投影误差

上面的线性方法通常先求相机位姿，再求空间点的位置，非线性优化方法同样可以用于求解相机位姿和 3D 点位置，不同的是，非线性优化会将它们都视为优化变量。

设三维空间点 P i = $X i , Y i , Z i$ T \mathbf{P_i}= $X_i,Y_i,Z_i$ ^T Pi= $Xi,Yi,Zi$ T ，其投影的像素坐标为 u i = $u i , v i$ T \mathbf{u_i}= $u_i,v_i$ ^T ui= $ui,vi$ T ，要计算相机位姿 R , t ( 其李群表示为 T ) R,t(\text{其李群表示为~}\mathbf{T}) R,t(其李群表示为 T) ，投影方程如下
s i $u i v i 1$ = K T $X i Y i Z i 1$ ( s i u i ) = K T P i s_i\begin{bmatrix}u_i\\v_i\\1 \end{bmatrix}=KT\begin{bmatrix}X_i\\Y_i\\Z_i\\1 \end{bmatrix}\\(s_iu_i)=KTP_i si uivi1 =KT XiYiZi1 (siui)=KTPi

于是我们可以构建最小二乘问题
T ∗ = arg ⁡ min ⁡ T 1 2 ∑ i = 1 n ∣ ∣ u i − 1 s i K T P i ∣ ∣ 2 2 T^*=\arg\underset{T}{\min}\frac{1}{2}\sum_{i=1}^n||u_i-\frac{1}{s_i}KTP_i||_2^2 T∗=argTmin21i=1∑n∣∣ui−si1KTPi∣∣22

其思路可以大致理解为：已知以目标在世界坐标系下的位置，利用估计的相机位姿将其转换为相机坐标系下的位置，再通过相机内参将其投影到图像平面，不断调整相机位姿的假设使投影点与实际观测点靠近

由于位姿属于李群，存在约束，所以可以先用李代数来参数化位姿，将其转化为无约束优化问题

定义 T = exp ⁡ ( ξ ∧ ) T=\exp(\xi^\wedge) T=exp(ξ∧) 其中 ξ = $ρ , ϕ$ T ∈ R 6 \xi= $\\rho,\\phi$ ^T\in \mathbb{R}^6 ξ= $ρ,ϕ$ T∈R6

则问题可重写为
ξ ∗ = arg ⁡ min ⁡ ξ 1 2 ∑ i = 1 n ∣ ∣ u i − π ( exp ⁡ ( ξ ∧ ) P i ) ∣ ∣ 2 \xi^*=\arg\underset{\xi}{\min}\frac{1}{2}\sum_{i=1}^n||u_i-\pi(\exp(\xi^\wedge)P_i)||^2 ξ∗=argξmin21i=1∑n∣∣ui−π(exp(ξ∧)Pi)∣∣2

在进行高斯牛顿法或者列文伯格-马夸尔特法进行优化之前，我们需要求每个误差项关于优化变量的导数。设定误差量为 e e e ，则有
e ( x + Δ x ) ≈ e ( x ) + J T Δ x e(x+\Delta x)\approx e(x)+J^T\Delta x e(x+Δx)≈e(x)+JTΔx

雅可比矩阵推导

重投影误差关于李代数的导数可表示为
∂ e ∂ δ ξ = ∂ e ∂ P ′ ∂ P ′ ∂ δ ξ \frac{\partial e}{\partial \delta\xi}=\frac{\partial e}{\partial P'}\frac{\partial P'}{\partial \delta\xi} ∂δξ∂e=∂P′∂e∂δξ∂P′

已知投影方程
u = f x X ′ Z ′ + c x v = f y Y ′ Z ′ + c y u=f_x\frac{X'}{Z'}+c_x \qquad v=f_y\frac{Y'}{Z'}+c_y u=fxZ′X′+cxv=fyZ′Y′+cy

求偏导
∂ e ∂ P ′ = − $\partial u \partial X ' \partial u \partial Y ' \partial u \partial Z ' \partial v \partial X ' \partial v \partial Y ' \partial v \partial Z '$ = − $f x Z ' 0 - f x X ' Z ' 2 0 f y Z ' - f y Y ' Z ' 2$ \frac{\partial e}{\partial P'}=-\begin{bmatrix}\frac{\partial u}{\partial X'}&\frac{\partial u}{\partial Y'}&\frac{\partial u}{\partial Z'}\\\frac{\partial v}{\partial X'}&\frac{\partial v}{\partial Y'}&\frac{\partial v}{\partial Z'}\end{bmatrix}=-\begin{bmatrix}\frac{f_x}{Z'}&0&-\frac{f_xX'}{Z'^2}\\0&\frac{f_y}{Z'}&-\frac{f_yY'}{Z'^2}\end{bmatrix} ∂P′∂e=− $\partialX'\partialu\partialX'\partialv\partialY'\partialu\partialY'\partialv\partialZ'\partialu\partialZ'\partialv$ =− $Z'fx00Z'fy-Z'2fxX'-Z'2fyY'$

根据李代数的左扰动模型
∂ P ′ ∂ δ ξ = $I , - P ' \land$ = $1 0 0 0 Z ' - Y ' 0 1 0 - Z ' 0 X ' 0 0 1 Y ' - X ' 0$ \frac{\partial P'}{\partial\delta\xi}=\begin{bmatrix}I,-P'^\wedge\end{bmatrix}=\begin{bmatrix}1&0&0&0&Z'&-Y'\\0&1&0&-Z'&0&X'\\0&0&1&Y'&-X'&0\end{bmatrix} ∂δξ∂P′= $I,-P'\land$ = 1000100010−Z′Y′Z′0−X′−Y′X′0

合并两部分即可得到雅可比矩阵
J = ∂ e ∂ P ′ ⋅ ∂ P ′ ∂ δ ξ = − $f x Z ' 0 - f x X ' Z ' 2 - f x X ' Y ' Z ' 2 f x + f x X ' 2 Z ' 2 - f x Y ' Z ' 0 f y Z ' - f y Y ' Z ' 2 - f y - f y Y ' 2 Z ' 2 f y X ' Y ' Z ' 2 f y X ' Z '$ J=\frac{\partial e}{\partial P'}\cdot\frac{\partial P'}{\partial \delta\xi}=-\begin{bmatrix} \frac{f_x}{Z'}&0&-\frac{f_xX'}{Z'^2}&-\frac{fxX'Y'}{Z'^2}&f_x+\frac{f_xX'^2}{Z'^2}&-\frac{f_xY'}{Z'}\\0&\frac{f_y}{Z'}&-\frac{f_yY'}{Z'^2}&-f_y-\frac{f_yY'^2}{Z'^2}&\frac{f_yX'Y'}{Z'^2}&\frac{f_yX'}{Z'} \end{bmatrix} J=∂P′∂e⋅∂δξ∂P′=− $Z'fx00Z'fy-Z'2fxX'-Z'2fyY'-Z'2fxX'Y'-fy-Z'2fyY'2fx+Z'2fxX'2Z'2fyX'Y'-Z'fxY'Z'fyX'$

如果仍需优化特征点的空间位置
∂ e ∂ P = ∂ e ∂ P ′ ∂ P ′ ∂ P \frac{\partial e}{\partial P}=\frac{\partial e}{\partial P'}\frac{\partial P'}{\partial P} ∂P∂e=∂P′∂e∂P∂P′

其中 ∂ e ∂ P ′ \frac{\partial e}{\partial P'} ∂P′∂e 在上方已求出，由于 P ′ = R P + t P'=RP+t P′=RP+t ，易得 ∂ P ′ ∂ P = R \frac{\partial P'}{\partial P}=R ∂P∂P′=R

因此：
∂ e ∂ P = − $f x Z ' 0 - f x X ' Z ' 2 0 f y Z ' - f y Y ' Z ' 2$ R \frac{\partial e}{\partial P}=-\begin{bmatrix}\frac{f_x}{Z'}&0&-\frac{f_xX'}{Z'^2}\\0&\frac{f_y}{Z'}&-\frac{f_yY'}{Z'^2}\end{bmatrix}R ∂P∂e=− $Z'fx00Z'fy-Z'2fxX'-Z'2fyY'$ R

优化算法代码实现

这里提供了大致代码的实现

高斯牛顿法：

cpp 复制代码

void optimizePoseGaussNewton(const std::vector<cv::Point3d>& points_3d, const std::vector<cv::Point2d>& points_2d, cv::Mat& K, Sophus::SE3d& pose)
{
    const int iterations = 10;                 // 最大迭代次数
    double cost = 0, last_cost = 0;            // 当前误差和上次迭代误差

    double fx = K.at<double>(0, 0);
    double fy = K.at<double>(1, 1);
    double cx = K.at<double>(0, 2);
    double cy = K.at<double>(1, 2);

    // 构建相机内参矩阵
    Eigen::Matrix3d K_eigen;
    K_eigen << fx,  0, cx,
                0, fy, cy,
                0,  0,  1;

    for (int iter = 0; iter < iterations; iter++)
    {
        Sophus::Matrix6d H = Sophus::Matrix6d::Zero();         // 初始化海森矩阵
        Sophus::Vector6d b = Sophus::Vector6d::Zero();         // 初始化梯度
        cost = 0;

        // 计算雅可比矩阵和残差
        for (size_t i = 0; i < points_3d.size(); i++)
        {
            // 将3D点转换到相机坐标系下
            Eigen::Vector3d pw(points_3d[i].x, points_3d[i].y, points_3d[i].z);
            Eigen::Vector3d pc = pose * pw;          // P_camera = T * P_world

            double X = pc[0], Y = pc[1], Z = pc[2];

            // 检查深度
            if (Z <= 0)
            {
                std::cerr << "Depth is zero or negative!" << std::endl;
                continue;
            }

            // 投影到图像平面并计算重投影误差
            Eigen::Vector3d pixel_homo = K_eigen * pc;          // 齐次坐标形式
            Eigen::Vector2d pixel(pixel_homo[0] / pixel_homo[2], pixel_homo[1] / pixel_homo[2]);     // 转换回像素坐标

            Eigen::Vector2d observerd(points_2d[i].x, points_2d[i].y);
            Eigen::Vector2d error = observerd - pixel;

            // 累加误差平方和
            cost += error.squaredNorm();

            // 计算雅可比矩阵
            Eigen::Matrix<double, 2, 6> J;

            J(0, 0) = fx / Z;
            J(0, 1) = 0;
            J(0, 2) = -fx * X / (Z * Z);
            J(0, 3) = -fx * X * Y / (Z * Z);
            J(0, 4) = fx + fx * X * X / (Z * Z);
            J(0, 5) = -fx * Y / Z;

            J(1, 0) = 0;
            J(1, 1) = fy / Z;
            J(1, 2) = -fy * Y / (Z * Z);
            J(1, 3) = -fy - fy * Y * Y / (Z * Z);
            J(1, 4) = fy * X * Y / (Z * Z);
            J(1, 5) = fy * X / Z;

            // 构建高斯-牛顿方程
            H += J.transpose() * J;
            b += -J.transpose() * error;
        }

        // 求解线性方程 H * dx = b
        Sophus::Vector6d dx;
        try
        {
            dx = H.ldlt().solve(b);   // H 明确是对称正定矩阵，使用 LDLT 分解求解
        }
        catch (const std::exception& e)
        {
            std::cerr << "Linear system solve failed: " << e.what() << std::endl;
            break;
        }

        // 检查解
        if (!dx.allFinite())
        {
            std::cerr << "Solution is not finite!" << std::endl;
            break;
        }

        // 检查收敛性
        if (iter > 0 && cost >= last_cost)
        {
            std::cout << "Iteration " << iter << ", cost increased: " << cost << " -> " << last_cost << std::endl;
            break;
        }

        // 更新位姿
        pose = Sophus::SE3d::exp(dx) * pose;

        // 更新误差
        last_cost = cost;

        // 输出迭代信息
        std::cout << "Iteration " << iter << ", cost = " << cost << std::endl;
        std::cout << "dx norm = " << dx.norm() << std::endl;

        // 判断收敛
        if (dx.norm() < 1e-6)
        {
            std::cout << "Converged in " << iter << " iterations." << std::endl;
            break;
        }
    }
}

列文伯格-马夸尔特优化法：

cpp 复制代码

void optimizePoseLM(const std::vector<cv::Point3d>& points_3d, const std::vector<cv::Point2d>& points_2d, cv::Mat& K, Sophus::SE3d& pose)
{
    // 前面直到计算雅可比矩阵和残差的部分与 Gauss-Newton 相同，不再重复
        // 自适应阻尼
        Sophus::Vector6d dx;
        bool updateAccepted = false;

        while (!updateAccepted)
        {
            try
            {
                // (H + lambda*I) * dx = b
                Sophus::Matrix6d H_lm = H + lambda * Sophus::Matrix6d::Identity();
                dx = H_lm.ldlt().solve(b);

                if (!dx.allFinite())
                {
                    throw std::runtime_error("Solution is not finite!");
                }
            }
            catch (const std::exception& e)
            {
                std::cerr << "Linear system solve failed: " << e.what() << std::endl;
                lambda *= 4;  // 增大阻尼因子，重新尝试
                continue;
            }

            // 尝试更新位姿
            Sophus::SE3d newPose = Sophus::SE3d::exp(dx) * pose;

            // 计算新的误差
            double newCost = 0;
            for (size_t i = 0; i < points_3d.size(); i++)
            {
                Eigen::Vector3d pw(points_3d[i].x, points_3d[i].y, points_3d[i].z);
                Eigen::Vector3d pc = newPose * pw;

                // 投影到图像平面并计算重投影误差
                Eigen::Vector3d pixel_homo = K_eigen * pc;
                Eigen::Vector2d pixel(pixel_homo[0] / pixel_homo[2], pixel_homo[1] / pixel_homo[2]);

                Eigen::Vector2d observerd(points_2d[i].x, points_2d[i].y);
                Eigen::Vector2d error = observerd - pixel;

                newCost += error.squaredNorm();
            }

            /*
             * 计算近似质量因子 ρ
             * ρ = [实际误差减少量] / [理论误差减少量]
             * 理论误差减少量 = -dx^T * (J^T * f + 0.5 * H * dx)
             * 简化后 ≈ dx^T * (λ * dx - b) (因为 H * dx ≈ λ * dx )
             */
            double modelImprovement = dx.dot(b - lambda * dx);
            double actualImprovement = cost - newCost;
            double rho = actualImprovement / modelImprovement;

            // 根据 ρ 调整阻尼因子
            if (rho > 0)
            {
                // 模型预测准确，接受更新
                pose = newPose;
                cost = newCost;
                updateAccepted = true;

                // 调整 λ：当模型很好时减少 λ，使模型更接近高斯-牛顿法
                lambda *= std::max(1.0 / 3.0, 1 - std::pow(2 * rho - 1, 3));
                lambda = std::max(lambda, 1e-6);  // 防止 λ 过小
            }
            else
            {
                // 模型预测不准确，拒绝更新
                lambda *= 2;  // 增大阻尼因子，重新尝试
                lambda = std::min(lambda, 1e5);  // 防止 λ 过大
            }

            // 防止无限循环
            if (lambda > 1e5)
            {
                std::cerr << "Lambda exploded! Exiting." << std::endl;
                break;
            }
        }

        // 输出迭代信息
        std::cout << "Iteration " << iter << ", cost = " << cost << ", lambda = " << lambda << std::endl;
        std::cout << "dx norm = " << dx.norm() << std::endl;

        // 判断收敛
        if (iter > 0 && cost >= last_cost - 1e-6)
        {
            std::cout << "Converged in " << iter << " iterations." << std::endl;
            break;
        }

        if (dx.norm() < 1e-6)
        {
            std::cout << "Converged in " << iter << " iterations." << std::endl;
            break;
        }

        // 更新误差
        last_cost = cost;
    }
}

这里建议搭配上一章的非线性优化一起看

3D-3D：ICP

当我们观测到两组 3D 点时（通过RGB-D相机或者三角化得到），我们可以直接使用 3D-3D 匹配点来估计相机运动

已知两组匹配 3D 点：
P = { p 1 , p 2 , ... , p n } , Q = { q 1 , q 2 , ... , q n } P=\{p_1,p_2,\dots,p_n\},\quad Q=\{q_1,q_2,\dots,q_n\} P={p1,p2,...,pn},Q={q1,q2,...,qn}

构建最小二乘问题
min ⁡ R , t 1 2 ∑ i = 1 n ∣ ∣ q i − ( R p i + t ) ∣ ∣ 2 \underset{R,t}{\min}\frac{1}{2}\sum_{i=1}^n||q_i-(Rp_i+t)||^2 R,tmin21i=1∑n∣∣qi−(Rpi+t)∣∣2

SVD 法求解

计算质心
μ p = 1 n ∑ i = 1 n p i , μ q = 1 n ∑ i = 1 n q i \mu_p=\frac{1}{n}\sum_{i=1}^np_i,\quad \mu_q=\frac{1}{n}\sum_{i=1}^nq_i μp=n1i=1∑npi,μq=n1i=1∑nqi
去中心化
p i ′ = p i − μ p , q i ′ = q i − μ q p_i'=p_i-\mu_p,\quad q_i'=q_i-\mu_q pi′=pi−μp,qi′=qi−μq
计算旋转矩阵

构建矩阵：
W = ∑ i = 1 n q i ′ p ′ i T W=\sum_{i=1}^nq_i'{p'}_i^T W=i=1∑nqi′p′iT

进行 SVD 分解
W = U Σ V T W=U\Sigma V^T W=UΣVT

则旋转矩阵可定义为
R = U V T R=UV^T R=UVT

（如果 det ⁡ ( R ) = − 1 \det(R)=-1 det(R)=−1 ，需要去负号修正： R = U ⋅ diag ( 1 , 1 , − 1 ) ⋅ V T R=U\cdot\text{diag}(1,1,-1)\cdot V^T R=U⋅diag(1,1,−1)⋅VT）

注：奇异值分解可以视为矩阵先进行了一次旋转 U U U ，沿着坐标轴进行缩放 Σ \Sigma Σ ，最后再进行一次旋转 V T V^T VT ，故旋转矩阵可以视为 R = U V T R=UV^T R=UVT
计算平移向量
t = μ q − R μ p t=\mu_q-R\mu_p t=μq−Rμp

SVD 法代码实现

cpp 复制代码

Sophus::SE3d solveICPSVD(const std::vector<Eigen::Vector3d>& pt1, const std::vector<Eigen::Vector3d>& pt2)
{
    // 1. 计算质心
    Eigen::Vector3d centroid1(0, 0, 0);
    Eigen::Vector3d centroid2(0, 0, 0);

    for (const auto& p : pt1) centroid1 += p;
    for (const auto& p : pt2) centroid2 += p;

    centroid1 /= pt1.size();
    centroid2 /= pt2.size();

    // 2. 去中心化
    Eigen::Matrix3d W = Eigen::Matrix3d::Zero();
    for (size_t i = 0; i < pt1.size(); ++i)
    {
        Eigen::Vector3d p1 = pt1[i] - centroid1;
        Eigen::Vector3d p2 = pt2[i] - centroid2;
        W += p1 * p2.transpose();
    }

    // 3. SVD分解
    Eigen::JacobiSVD<Eigen::Matrix3d> svd(W, Eigen::ComputeFullU | Eigen::ComputeFullV);
    Eigen::Matrix3d U = svd.matrixU();
    Eigen::Matrix3d V = svd.matrixV();

    // 4. 计算旋转矩阵
    Eigen::Matrix3d R = V * U.transpose();

    // 5. 检查旋转矩阵的行列式
    if (R.determinant() < 0)
    {
        Eigen::Matrix3d V_fixed = V;
        V_fixed.col(2) *= -1;  // 翻转第二列
        R = V_fixed * U.transpose();
    }

    // 6. 计算平移向量
    Eigen::Vector3d t = centroid2 - R * centroid1;

    return Sophus::SE3d(R, t);
}

当然也可以通过非线性优化来求解，和上面大差不差，这里就不赘述了

特性	对极几何（2D-2D）	PnP（3D-2D）	ICP（3D-3D）
输入	两帧图像的2D特征匹配点	3D地图点+当前帧的2D检测	两组3D点云
输出	相机相对运动位姿（R、t）特征点深度	相机位姿（R、t）	点云间的刚体变换（R、t）
适用场景	单目相机SLAM初始化、双目相机	已知地图定位	RGB-D相机SLAM、激光SLAM、点云配准
退化情况	纯旋转运动，匹配点共面、无纹理区域	匹配点共面、观测点噪声过高	点云特征不明显、初始位姿偏差过大
常用算法	八点法、五点法、RANSAC+八点法	P3P、EPnP、DLT、非线性优化	SVD、非线性优化