3DGS 如何理解它？

3dgs

---

3DGS即是3D Gaussian Splatting。

出自2023年的一篇名为《3D Gaussian Splatting for Real-Time Radiance Field Rendering》（[[3D Gaussian Splatting for Real-Time Radiance Field Rendering.pdf]]），作者是BERNHARD KERBL和GEORGIOS KOPANAS。原文我看了几遍，也在win11环境下跑了一遍（[[3dgs复现-从零搭建]]）。但是由于自身在图形学相关知识的欠缺，仍然一头雾水。

其中几个关键字包括但不限于：3D高斯球、球谐函数、α blending、各向异性、自适应密度控制等等...我都不甚了解。

1 整体流程

首先需要给自己一个定义，3dgs到底是在做什么？

!NOTE\] 我的简单理解 3DGS 是使用 3D Gaussian 球表示三维场景，并通过 Splatting 技术渲染出来。

先从实现流程梳理一遍3dgs，下图是原文给出的pipeline图：

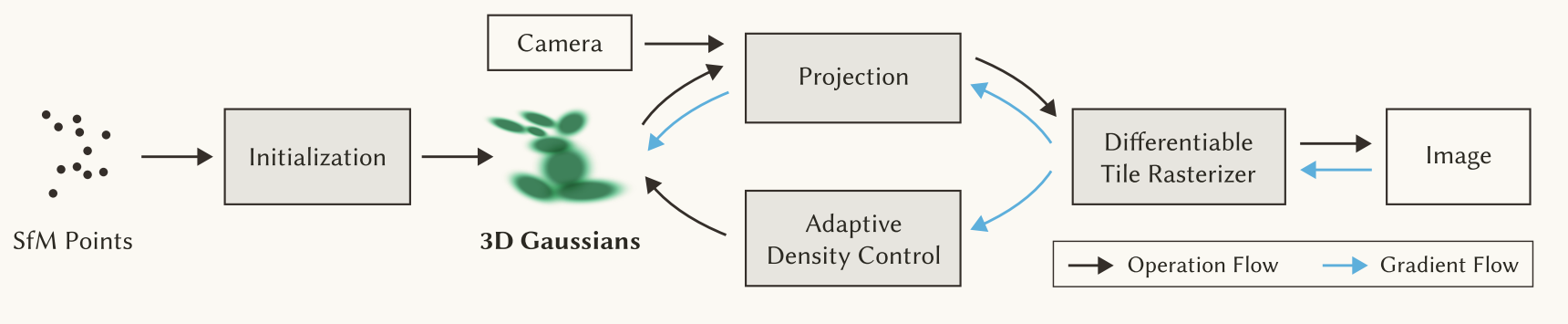
从图中可以主要是三个部分的转换：sfm points -> 3D gaussians -> image。

其中sfm points到3D gaussians即是3dgs的初始化，也就是说原来我用点云表示的场景，我如何转换到3d高斯椭球表示？这里先不细究为什么要用3d高斯椭球，以及如何转换的事情？

接下来，是3d高斯椭球到2D图像的转换。这一步是整个流程的关键。这里做的工作也就是光栅化，就是做的splatting的工作。如果把3d高斯椭球看成一个雪球，图片是一面墙，那么splatting应该是一个把雪球扔到墙上的动作。这一部分原理应该是来自2001年的[[EWASplatting-TVCG02.pdf]]。这部分涉及比较多的图形学和数学知识，深入理解，需要推导相关公式。（先留一个buffer,后续再看）

整个流程大概就是这样。其中，如何==使得splatting的结果和真实图像看起来更像？==那么就需要进一步的优化3D高斯椭球的位置、形状、颜色等等可以表征3D高斯椭球的参数。

进一步发问，3D高斯椭球有哪些参数？

简单来说，应该至少有3维位置信息 μ （ x , y , z ） \mu（x,y,z） μ（x,y,z），以及缩放、旋转、颜色等信息吧。

==那又如何优化这些参数呢？==通过原文附录B的算法流程，3dgs是将光栅化后的图片和原始图片计算Loss值，使用Adam优化3D高斯椭球的各种参数。其中的IsRefinementIteration函数，就是原文5.2节提到的自适应密度控制。这一部分也是我看论文一直没有搞懂的部分。

至此，我大概懂了3dgs在做的事情。总结一下，3dgs的算法主要是三个部分：

1. 引入3D gaussian作为 3D 表示；
2. 高斯球的自适应密度控制；
3. 高斯球的快速可微光栅化渲染器的实现；
   结合原文给出的pipeline图，更好理解。

2 3DGS的场景表示

2.1 三维高斯

原文中对这部分提及较少，前置知识需要补充一下。

首先，一维高斯也是正态分布:
f （ x ） = 1 2 π σ e x p − ( x − μ ) 2 2 σ 2 f（x）= \frac{1}{\sqrt{2\pi }\sigma }exp^{-\frac{\left ( x-\mu \right )^{2} }{2\sigma^{2} } } f（x）=2π σ1exp−2σ2(x−μ)2

这一点，还是比较熟悉的。其中：

• (x)：随机变量。
• ( μ \mu μ)：均值（mean），决定分布的中心位置。
• ( σ \sigma σ)：标准差（standard deviation），决定分布的宽度。
• ( σ 2 \sigma^2 σ2) ：方差（variance），表示数据的离散程度。
  同样的思想，二维高斯分布的图形是一个椭圆，三维高斯分布的图形是一个椭球 ，这个椭球分别以xyz轴对称。概率论中学的三元正态分布函数通常写成：
  N μ x , σ x , μ y , σ y , μ z , σ z ( x , y , z ) = 1 2 π 3 σ x σ y σ z exp ⁡ ( − ( x − μ x ) 2 2 σ x 2 − ( y − μ y ) 2 2 σ y 2 − ( z − μ z ) 2 2 σ z 2 ) N_{\mu_{x},\sigma_{x},\mu_{y},\sigma_{y},\mu_{z},\sigma_{z}}\left(x,y,z\right)=\frac{1}{\sqrt{2\pi}^{3}\sigma_{x}\sigma_{y}\sigma_{z}}\exp\left(-\frac{\left(x-\mu_{x}\right)^{2}}{2\sigma_{x}^{2}}-\frac{\left(y-\mu_{y}\right)^{2}}{2\sigma_{y}^{2}}-\frac{\left(z-\mu_{z}\right)^{2}}{2\sigma_{z}^{2}}\right) Nμx,σx,μy,σy,μz,σz(x,y,z)=2π 3σxσyσz1exp(−2σx2(x−μx)2−2σy2(y−μy)2−2σz2(z−μz)2)

这个形式其实是这三个变量为互不相关的独立变量 且椭球的坐标系和世界坐标系平行 的情况。但是原文中的3D高斯椭球是可以旋转，所以它的对称轴（称为 模型坐标系 ）不一定和世界坐标系重叠。对称轴不和世界坐标系重叠的多元正态分布意味着各随机变量相互之间并不是独立变量。（这里为什么，后续再细究）总之，这里不止有 μ x \mu_{x} μx, μ y \mu_{y} μy, μ z \mu_{z} μz,还有 μ x y \mu_{xy} μxy
μ x z \mu_{xz} μxz等等。（先留一个buffer,后续再看）

换一种定义形式：
G s ( x ) = 1 2 π 3 det ⁡ ( Σ ) ⋅ e − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) G_s\left(\boldsymbol{x}\right)=\frac{1}{\sqrt{2\pi}^3\det(\Sigma)}\cdot e^{-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^T\Sigma^{-1}(\boldsymbol{x}-\boldsymbol{\mu})} Gs(x)=2π 3det(Σ)1⋅e−21(x−μ)TΣ−1(x−μ)

这里 x x x不是x方向坐标，而是3维中一个点x, det ⁡ ( Σ ) \det(\Sigma) det(Σ)是协方差矩阵的行列式。

然后，这里有一些公式推导。背景知识需要学习GAMES101-现代计算机图形学入门-闫令琪。（先留一个buffer,这部分我还在学习）

总之，这里给出的结论就是可以使用协方差矩阵来控制椭球的形状。因为任意高斯都可以看做是标准高斯通过仿射变换得到，所以任意椭球都可以看作是球通过仿射变换得到。而协方差矩阵是可以通过旋转和缩放矩阵来表达的，表示了这个3D高斯在各个坐标轴的缩放以及旋转。

由于3D高斯的协方差矩阵必须满足半正定，而直接学习协方差矩阵很难满足这个条件，不能用传统梯度下降法，或者说不能将协方差矩阵作为一个优化参数直接优化。所以在实现中，是先学习高斯的旋转矩阵和缩放矩阵，再通过他们构造对应的协方差矩阵；那么不直接对协方差矩阵优化，而是将R,S作为优化参数优化，就可以保持协方差矩阵的正半定。也即是原文中的公式6：
Σ = R S S T R T \Sigma =RSS^{T} R^{T} Σ=RSSTRT

• R是四元数表示的旋转矩阵（此矩阵要保持normalization）
• S是一个对角缩放矩阵，其对角线上是协方差矩阵三个特征值的平方根
  3D高斯椭球的参数应该还有R 和 S组合表达的协方差矩阵。R通过四元数表示，4个参数，S为对角矩阵，3个参数，所以协方差一共7个参数

2.2 球谐函数

文中说使用球谐函数来表示颜色，而且文中说这种表示方法可以使得高斯椭球具有各向异性的性质。我的理解是不同方向看起来是否一致。纯色球体显然就是各向同性。

球谐函数的理解可以类比于基函数。任何一个函数可以用正弦和余弦函数的线性组合来近似。任何一个球面坐标函数也可以用多个球谐函数来近似。

这里深入理解，同样有许多公式需要仔细推导。简单来说，这里原文使用了4阶球谐函数来表征椭球颜色。而且RGB需要3 * 16个参数来近似。

2.3 α blending

优化的参数包括：

• 中心位置：3dof
• 协方差矩阵：7dof
• 透明度：1dof
• 球谐系数：48 dof(J = 3，16 * 3)
  所以每个高斯椭球有59个参数需要优化。

3 可微光栅化

可微光栅化是 3DGS 实现实时渲染 和梯度优化的关键。它的核心任务是将 3D 空间中的 高斯椭球（3D Gaussians）投影到 2D 图像平面，并以可微分的方式计算颜色和透明度，从而允许梯度流回传到 3D 高斯参数进行优化。

3.1 坐标变换

在计算机图形学中，将 3D 对象渲染到 2D 屏幕需要一系列的坐标系转换。对于 3DGS 而言，最关键的一步是将 3D 高斯椭球的协方差矩阵（ Σ \Sigma Σ）投影到 2D 图像平面 ，得到一个 2D 高斯（通常是一个椭圆）的协方差矩阵（ Σ ′ \Sigma' Σ′）。

投影协方差矩阵

根据原文（公式 5），3D 协方差矩阵 Σ \Sigma Σ 投影到 2D 屏幕空间的协方差矩阵 Σ ′ \Sigma' Σ′ 的计算公式为：
Σ ′ = J W Σ W T J T \Sigma' = J W \Sigma W^T J^T Σ′=JWΣWTJT

• Σ \Sigma Σ：原始的 3D 协方差矩阵，定义了 3D 高斯椭球的形状和方向。
• W W W：视图变换矩阵（View Transform），将 3D 世界坐标系下的点/向量转换到相机坐标系下。
• J J J ：透视投影雅可比矩阵（Jacobian of the perspective projection）。它反映了相机坐标系下微小的 3D 变化如何影响 2D 屏幕坐标系下的变化。
• Σ ′ \Sigma' Σ′ ：投影后的 2D 协方差矩阵，它定义了 2D 屏幕上椭圆的形状和大小。
  这个公式的意义在于，它将3D 椭球在相机视角下的投影 直接计算为一个2D 椭圆，而不是先将 3D 椭球细分成许多点或三角形再进行投影。

我的理解 ：这就像是直接计算雪球（3D 高斯）被扔到墙上（2D 屏幕）后，其模糊边缘的形状 （2D 椭圆）和中心点。

3.2 着色和混合（Coloring and Blending）

将 3D 高斯投影到 2D 屏幕后，算法需要确定每个 2D 投影高斯自身的颜色 和透明度 ，然后将它们按深度顺序 进行混合（Blending）。

a. 颜色计算（Color Calculation）

每个 3D 高斯中心的颜色是通过**球谐函数（Spherical Harmonics, SH）**计算的。

• 各向异性 ：如你所说，SH 函数的引入使得高斯具有各向异性 （Anisotropic）的性质。这意味着从不同方向 观察同一个高斯时，它呈现的颜色是不同的，这极大地提高了对光照、阴影和高光的表达能力。
• 计算过程 ：根据相机方向 （即观察方向 v \boldsymbol{v} v），将预先存储在每个高斯中的 SH 系数（ 48 48 48 个参数）解码，得到该视角下的 RGB 颜色 c \boldsymbol{c} c。

b. 透明度（Opacity）

每个高斯有一个优化的参数：透明度（ α \alpha α） ，在原文中称为 不透明度（Opacity） o o o 。这个参数在 ( 0 , 1 ) (0, 1) (0,1) 之间。

c. α \alpha α Blending（阿尔法混合）

这是 3DGS 渲染的核心步骤，决定了如何将多个 2D 高斯混合起来形成最终像素颜色。

也就是文中提及的 α \alpha α Blending ，3DGS 采用了一种称为体渲染（Volume Rendering）的累积方式，但简化成了基于深度排序 的 α \alpha α 混合。

1. 深度排序 ：首先，所有与视锥体相交的 2D 高斯必须根据其中心点 到相机的深度（ z z z 值）进行排序 ，从后往前 （far to near）依次处理。这是处理透明度混合的关键，以保证物理上的正确性（远处的物体先被光线穿透）。
2. 累积颜色（Accumulated Color） ：对于图像平面上的一个像素 ，遍历所有覆盖它的 2D 高斯，从后往前累积颜色 。其计算公式是经典的体渲染 离散化公式：
   C = ∑ i c i α i ∏ j = 1 i − 1 ( 1 − α j ) C = \sum_{i} \boldsymbol{c}i \alpha_i \prod{j=1}^{i-1} (1 - \alpha_j) C=i∑ciαij=1∏i−1(1−αj)
   其中：

• C C C：该像素的最终颜色。
• c i \boldsymbol{c}_i ci ：第 i i i 个高斯（从后往前排序）的 RGB 颜色（由 SH 函数计算得到）。
• α i \alpha_i αi ：第 i i i 个高斯对该像素的贡献透明度 。这个透明度是高斯本身的透明度 o i o_i oi 和 2D 高斯投影（ Σ ′ \Sigma' Σ′）在该像素位置的密度值 （即高斯函数的概率密度值）相乘的结果。
• ∏ j = 1 i − 1 ( 1 − α j ) \prod_{j=1}^{i-1} (1 - \alpha_j) ∏j=1i−1(1−αj) ：这是透射率（Transmittance） ，表示光线穿过前 i − 1 i-1 i−1 个高斯后剩余的强度。
  这个 α \alpha α 混合过程完全可微分 ，意味着我们可以在渲染结束后计算最终颜色 C C C 对所有 高斯参数（ μ , R , S , o , S H \mu, R, S, o, SH μ,R,S,o,SH）的梯度。

3.3 光栅化（Rasterization）

光栅化的工作是高效地实现 3.1 坐标变换 和 3.2 着色混合的过程。

1. 块状处理（Tiling）和排序

• Tile/Binning ：为了避免遍历所有高斯，3DGS 将 2D 屏幕划分为 16 × 16 16 \times 16 16×16 或 32 × 32 32 \times 32 32×32 的小块（Tiles）。每个高斯只会被分配到它覆盖的那些 Tile 中。
• 快速深度排序 ：在高斯数量庞大时（数百万个），快速进行深度排序 至关重要。原文中利用 GPU 的并行能力和 Radix Sort 等高效算法，实现了快速的从后往前排序。

2. GPU 实现

3DGS 的核心优势在于它将上述所有步骤（特别是 α \alpha α 混合）完全放在 GPU 上并行实现：

• GPU 几何着色器（Geometry Shader） ：将 3D 高斯投影为 2D 椭圆并计算 Σ ′ \Sigma' Σ′。
• GPU 像素着色器（Pixel Shader） ：在每个像素上，根据深度排序 后的高斯列表，执行 α \alpha α 混合公式，计算最终颜色。
  这种高度并行的 GPU 实现，配合可微分的 α \alpha α 混合公式，是 3DGS 达到实时高画质渲染的关键。

---

4 优化与自适应密度控制（Optimization and Adaptive Density Control）

3D 高斯椭球的参数 和如何优化这些参数 ，以及对自适应密度控制 的困惑，是3DGS 能达到高质量重建的学习部分。

4.1 3D 高斯椭球的参数

再次总结优化的参数，每个高斯有 59 个参数需要优化：

参数类别 (Parameter)	含义 (Meaning)	参数量 (Count)	备注 (Note)
中心位置 ( μ \boldsymbol{\mu} μ)	3D 位置	3	x , y , z x, y, z x,y,z
旋转 ( R R R)	四元数表示	4	保持单位长度 (Normalization)
缩放 ( S S S)	对角矩阵的对角线元素	3	表达协方差大小
不透明度/透明度 ( o o o)	基础透明度	1	经 σ \sigma σ 激活后 ∈ ( 0 , 1 ) \in (0, 1) ∈(0,1)
球谐函数系数 ( S H SH SH)	颜色表示 (4阶)	3 × 16 = 48 3 \times 16 = 48 3×16=48	R/G/B 各 16 个系数
总计		59

4.2 参数优化：通过可微分渲染实现

优化过程采用基于梯度的优化（Adam Optimizer）。

1. 损失函数（Loss Function） ：计算渲染图像 I r e n d e r I_{render} Irender 和 真实图像 I g t I_{gt} Igt 之间的差异。原文使用 L 1 L_1 L1 损失（感知质量）和 D-SSIM（结构相似度）的组合：
   L = λ 1 L 1 + λ s s i m L D − S S I M L = \lambda_1 L_{1} + \lambda_{ssim} L_{D-SSIM} L=λ1L1+λssimLD−SSIM

2. 反向传播 ：利用可微光栅化 （特别是 α \alpha α 混合公式）计算 ∂ L ∂ Parameter \frac{\partial L}{\partial \text{Parameter}} ∂Parameter∂L。梯度从 2D 屏幕流回 3D 高斯的 59 59 59 个参数。

3. Adam 优化 ：使用 Adam 优化器 沿着梯度方向更新每个高斯的 59 59 59 个参数。

4.3 自适应密度控制 (Adaptive Density Control)

这是 3DGS 超越 NeRF 的一个关键创新点，对应于原文的 5.2 5.2 5.2 节和附录 B B B 中的 IsRefinementIteration 函数。

它解决了如何自动调整高斯数量和大小来适应场景的细节和空旷区域的问题。

核心思想：两个动作

自适应控制主要基于两个动作：克隆/分裂（Clone/Split）和淘汰（Remove）。

动作 (Action)	触发条件 (Trigger Condition)	目的 (Purpose)
1. 分裂/克隆	高斯太大使渲染误差大	增加细节（细分）
	a. 分裂 (Split) ：高斯 Σ \Sigma Σ 的缩放因子过大    ⟹    \implies ⟹ 新高斯为旧高斯的一半大。
	b. 克隆 (Clone) ：高斯 Σ \Sigma Σ 缩放因子较小，但梯度较大    ⟹    \implies ⟹ 新高斯大小不变。
2. 淘汰/重置	高斯不重要	减少冗余、清除噪声
	a. 淘汰 (Remove) ：透明度 o o o 接近 0    ⟹    0 \implies 0⟹ 清除隐形或冗余的高斯。
	b. 重置透明度 ：定期将透明度 o o o 重置为一个较小值，迫使高斯在优化中重新"学习"其重要性。

触发时机

• 定期执行 ：并非每一步优化都执行，而是在每隔 N N N 步 （例如 100 100 100 步）优化后，检查高斯的平均位置梯度 和透明度。
• 根据梯度决定 ：对于位置梯度 过大的高斯（意味着它附近的几何或颜色变化剧烈，一个高斯不足以表达），就执行分裂或克隆，以增加该区域的表示能力。

总结 ：自适应密度控制就是让模型边学边调整 ：在细节丰富、渲染误差大的地方增加高斯 （分裂/克隆）；在空旷区域或表示不佳的地方移除高斯（淘汰）。

---