一、概述
考虑这样一种问题:
现有一个由 N N N 个整数组成的数列 A A A,满足 ∀ 1 ≤ i ≤ n , a i ∈ [ − 1 0 9 , 1 0 9 ] \forall 1 \le i \le n, \space a_i \in [-10^9, 10^9] ∀1≤i≤n, ai∈[−109,109]。
接下来你要进行 Q Q Q 次操作,单次操作有两种类型:
- 1 l r x 1 \space l \space r \space x 1 l r x ,表示 ∀ i ∈ [ l , r ] , a i ← a i + x \forall i \in [l,r], a_i \leftarrow a_i+x ∀i∈[l,r],ai←ai+x ;
- 2 l r 2 \space l \space r 2 l r ,你应该输出 ∑ i = l r a i \displaystyle\sum_{i=l}^{r}{a_i} i=l∑rai 。
对于每个 2 2 2 类操作,输出其答案。
如果使用暴力算法求解,则直接进行操作,复杂度为 O ( N 2 ) O(N^2) O(N2) 。如果我们可以使用树状数组 (Fenwick Tree)求解,则时间复杂度可以降低至 O ( N log N ) O(N \log N) O(NlogN) 。
二、 lowbit 函数的定义和原理
1. 定义
l o w b i t ( x ) \mathrm{\bold{lowbit}}(x) lowbit(x) 函数是指由一个数 x x x 在二进制下最后一个 1 1 1 以及后面的 0 0 0 组成的数。例如, l o w b i t ( 24 ) = 8 , l o w b i t ( 16 ) = 16 \mathrm{lowbit}(24)=8, \space \mathrm{lowbit}(16)=16 lowbit(24)=8, lowbit(16)=16 。
2. 性质及求法
使用 l o w b i t \mathrm{lowbit} lowbit 函数可以遍历二进制下一个整数 x x x 的每一个 1 1 1 。例如,我们对 15 = ( 1111 ) 2 15=(1111)_2 15=(1111)2 进行操作,每一次减少它的 l o w b i t \mathrm{lowbit} lowbit ,则它的变化如下:
15 → 14 → 12 → 8 → 0 15 \rightarrow 14 \rightarrow 12 \rightarrow 8 \rightarrow 0 15→14→12→8→0
C++代码如下:
cpp
inline void lowbit(int x)
{
for (int i = x; i; i -= lowbit(i)) // lowbit(i) 的实现将在后面介绍
{
// do something
}
}下面介绍 l o w b i t \mathrm{lowbit} lowbit 函数的求法。
我们可以运用计算机二进制补码的性质,补码即反码加上一,由于反码的每一位都和原码不同,故补码中的最后一个 1 1 1 与原码中的最后一个 1 1 1 重合。因此, 补码 & 原码 的操作就可以实现求 lowbit ,时间复杂度为 O ( 1 ) O(1) O(1) 。
实现方法如下:
cpp
#define lowbit(x) x & (-x) // -x : x 的补码
#define lowbit(x) x & (~x + 1) // ~x + 1: x 的反码加一(补码)例如:二进制下 14 14 14 的 l o w b i t \mathrm{lowbit} lowbit 求法:
14 = ( 1110 ) 2 − 14 = ( 111 ⋯ 0010 ) 2 ⇒ 14 & ( − 14 ) = ( 10 ) 2 = 2 \begin{align*} 14&=(1110)_2 \\ -14&=(111 \cdots 0010)_2 \\ \Rightarrow 14\space \&\space (-14) &= (10)_2=2 \end{align*} 14−14⇒14 & (−14)=(1110)2=(111⋯0010)2=(10)2=2
经验证,结果正确。
3. 应用
因为二进制的 l o w b i t \mathrm{lowbit} lowbit 函数具有较强的位处理特性,所以常被用来处理与二进制有关的问题,例如在状态压缩 DP 中, l o w b i t \mathrm{lowbit} lowbit 函数可以减少不必要的计算,直接提取每一个有效位数,减少时间复杂度; l o w b i t \mathrm{lowbit} lowbit 函数还可以用来解决一些倍增问题,将问题的时间复杂度从 ≥ O ( n ) \ge O(n) ≥O(n) 量级优化为 O ( log n ) O(\log n) O(logn) 量级。
接下来, l o w b i t \mathrm{lowbit} lowbit 函数将会被广泛地使用于树状数组中,解决各类问题。
三、树状数组的单点修改和区间查询
1. 树状数组的实现原理
树状数组既不是树,也不是数组,是一种特殊的数据结构。树状数组的一个节点 c x c_x cx 保存序列 A A A 的区间 [ x − l o w b i t ( x ) + 1 , x ] [x - \mathrm{lowbit}(x)+1,x] [x−lowbit(x)+1,x] 内所有元素的总和,即 c x = ∑ i = x − l o w b i t ( x ) + 1 x a i c_x= \displaystyle\sum_{i=x - \mathrm{lowbit}(x)+1}^{x}{a_i} cx=i=x−lowbit(x)+1∑xai 。通过一次保存一个 l o w b i t \mathrm{lowbit} lowbit 之内所有的数值,我们可以实现缩小查找需要的时间。树状数组的示例图如下:
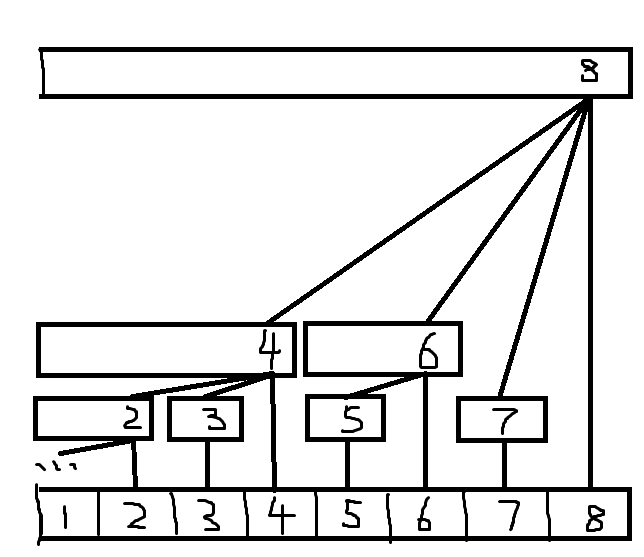
若记一个节点 x x x 的子节点的集合为 s ( x ) s(x) s(x) ,树状数组满足以下几个性质:
- c x = ∑ y ∈ s ( x ) y c_x=\displaystyle\sum_{y \in s(x)}{y} cx=y∈s(x)∑y
- ∣ s ( x ) ∣ = log 2 l o w b i t ( x ) |s(x)|=\log_2\mathrm{lowbit}(x) ∣s(x)∣=log2lowbit(x)
- c x c_x cx 的父节点是 c x + l o w b i t ( x ) c_{x+\mathrm{lowbit}(x)} cx+lowbit(x)
- 树的深度 ≤ O ( log n ) \le O(\log n) ≤O(logn) 。
2. 树状数组的插入操作
要给一个数增加一个特定的值,则这个数的位置之后的前缀和也会相应的增加这个值。根据这个原理以及树状数组的性质 2,3,我们可以使用 l o w b i t \mathrm{lowbit} lowbit 函数定义树状数组的插入操作:
cpp
inline void add(int x, int v)
{
for (; x <= N; x += lowbit(x))
tr[x] += v;
}3. 树状数组的求和操作
由树状数组的性质 1,知要求 ∑ i = 1 n a i \displaystyle\sum_{i=1}^{n}a_i i=1∑nai 的时候,只需要遍历每一个 l o w b i t ( n ) \mathrm{lowbit}(n) lowbit(n) 即可。
cpp
inline int query(int x)
{
int res = 0;
for (; x; x -= lowbit(x))
res += tr[x];
return res;
}4. 完整代码实现
cpp
#define lowbit(x) x & (-x)
template <class _Tp>
class FenwickTree
{
private:
int tr[N];
public:
inline void add(int x, _Tp v)
{
for (; x <= N; x += lowbit(x))
tr[x] += v;
}
inline _Tp query(int x)
{
_Tp res = 0;
for (; x; x -= lowbit(x))
res += tr[x];
return res;
}
}参考文献:
- 《算法竞赛进阶指南》0x42 树状数组,李煜东
- OI Wiki 网站树状数组部分