LeetCode——三指针

2367. 等差三元组的数目

思路

对于i来言，从左到右遍历，数是递增的。也就是找到下一个数num[j] - nums[i] == diff以及nums[k] - nums[i] == 2 * diff。简化成双指针，随着i的增加，每次调整j、k使之满足条件即可
代码

java 复制代码

class Solution {
    public int arithmeticTriplets(int[] nums, int diff) {
        int n = nums.length, ans = 0, i = 0, j = 0;
        for (int num : nums) {
            while (i < n && num + diff > nums[i]) { // 找到>=的数
                i ++;
            }
            if (i >= n || num + diff < nums[i]) continue;
            while (j < n && num + 2 * diff > nums[j]) {
                j ++;
            }
            if (j < n && num + 2 * diff == nums[j]) {
                ans ++;
            }
        }
        return ans;
    }
}

2563. 统计公平数对的数目

思路

数对而言，没有相应顺序要求，因此不妨给数组进行排序。对于lower <= nums[i] + nums[j] <= upper。可以拆解为

nums[i] + nums[j] >= lower
nums[i] + nums[j] <= upper两段
nums[i]是递增的，因此可以从后往前找到第一个lj满足nums[i] + nums[lj] >= lower，以及找到第一个rj满足nums[i] + nums[rj] > upper.计数rj - lj;
代码

java 复制代码

class Solution {
    public long countFairPairs(int[] nums, int lower, int upper) {
        Arrays.sort(nums);
        long ans = 0;
        int lj = nums.length, rj = nums.length, n = nums.length;
        for (int i = 0; i < n; i ++) { // 递增
            while (rj > 0 && nums[rj - 1] > upper - nums[i]) rj --; // 递减
            while (lj > 0 && nums[lj - 1] >= lower - nums[i]) lj --; // 递减
            ans += Math.min(rj, i) - Math.min(lj, i);
        }
        return ans;
    }
}

以上是可以转换成双指针的做法，下面这种则是通过一次遍历维护某种性质的做法

795. 区间子数组个数

思路

枚举子数组的右边界，需要确定左边界的范围。左边界应该是nums[l]刚好大于right，nums[r]大于等于left.

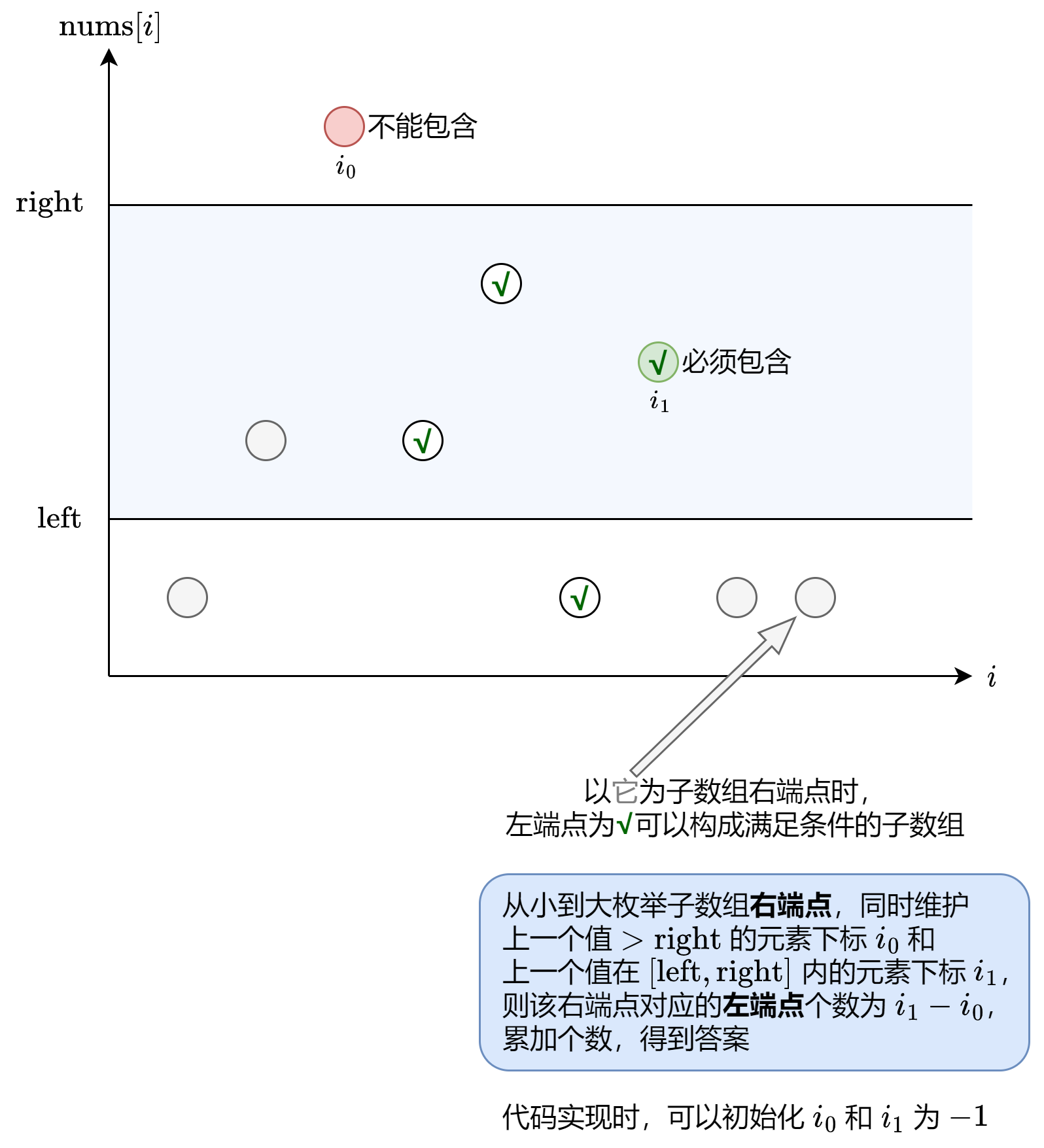
代码

java 复制代码

class Solution {
    public int numSubarrayBoundedMax(int[] nums, int left, int right) {
        int n = nums.length, ans = 0, l = -1, r = -1;
        for (int i = 0; i < n; i ++) { // 表示以i为右端点的子数组
            if (nums[i] > right) l = i; // 保证不能存在大于right的存在，右边界
            if (nums[i] >= left) r = i; // 记录其中最近的>= left的数存在，左边界
            ans += (r - l);
        }
        return ans;
    }
}

2444. 统计定界子数组的数目

思路

枚举子数组的右边界，右边界位于最近位于上一个不在[minK, maxK]区间值的索引i0,与min(minIndex, maxIndex)之间
代码

java 复制代码

class Solution {
    public long countSubarrays(int[] nums, int minK, int maxK) {
        int n = nums.length, minIndex = -1, maxIndex = -1, i0 = -1;
        long ans = 0;
        for (int i = 0; i < n; i ++) {
            if (nums[i] < minK || nums[i] > maxK) i0 = i;
            if (nums[i] == minK) minIndex = i;
            if (nums[i] == maxK) maxIndex = i;
            ans += Math.max(Math.min(minIndex, maxIndex) - i0, 0);
        }
        return ans;
    }
}