前缀和一维/二维-复习篇

一维

前缀和标志循环

java 复制代码

	for(int i=1;i<n;i++) {
			sum[i]=sum[i-1]+a[i];
		}

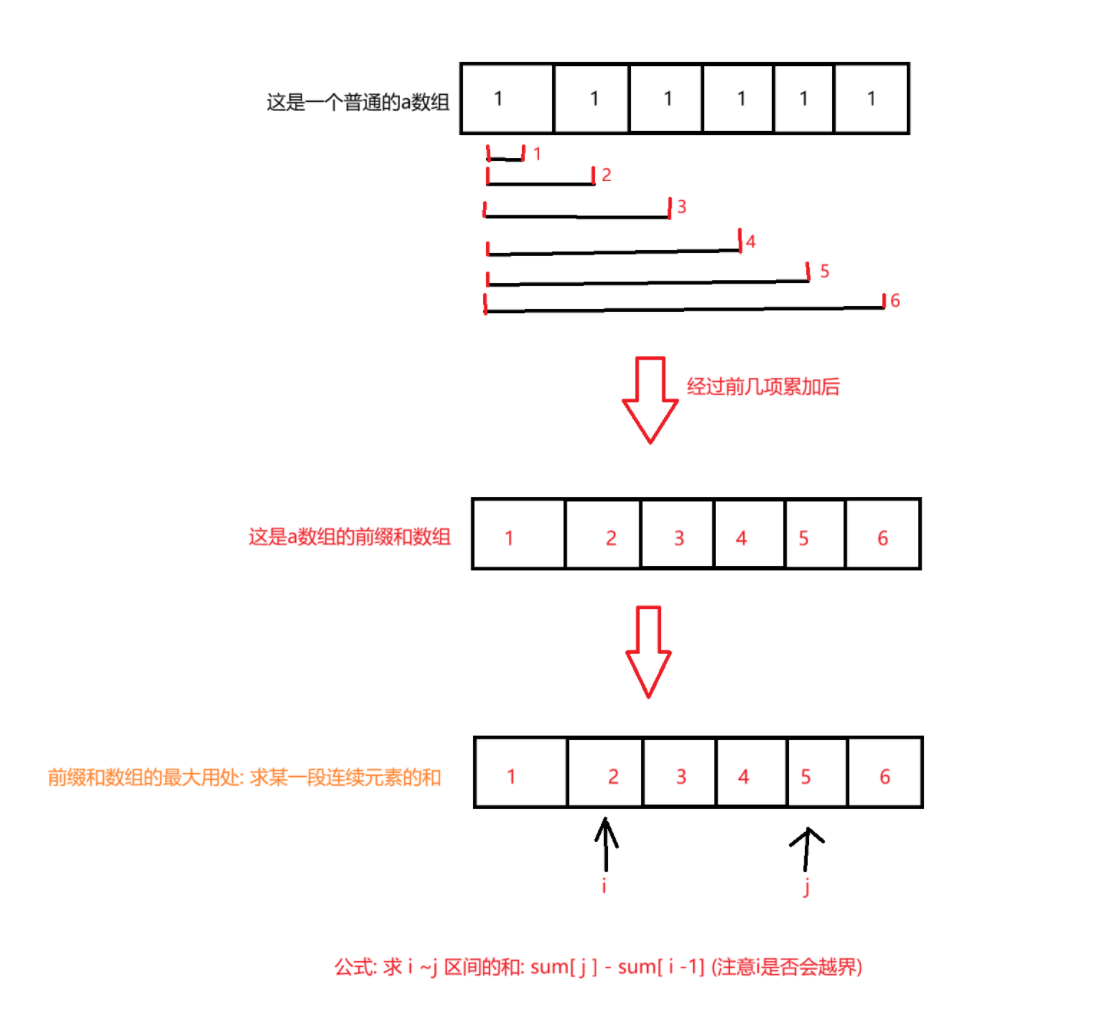
其实一维前缀和, 对于我自己来说, 最值得让我写的不是他的思想, 因为他的思想很简单: 就是这几个大字 "创建前缀和数组, 循环累加, 求前几项的和" 这就是前缀和.

但是我在真实运用的时候,也就是写题的时候不会纠结于他的思想, 而是" 这个前缀和数组到底该从0下标开始用, 还是从1下表开始用" ,这是我所纠结的, 因为以前总是忘记随手就写了,后面发现其实随手写的并不优雅, 索性今天一次性总结完, 以绝后患

java 复制代码

//第一种写法:从0下标开始用
	static int[] solve(int[] a) {
		int n = a.length;
		int[] sum = new int[n];
		sum[0] =a[0];
		
		for(int i=1;i<n;i++) {
			sum[i]=sum[i-1]+a[i];
		}
		return sum;
	}
	//第一种写法:从1下标开始用
	static int[] solve2(int[] a) {
		int n = a.length;
		int[] sum = new int[n+1];
		
		for(int i=1;i<n+1;i++) {
			sum[i]=sum[i-1]+a[i-1];
		}
		return sum;
	}

以上两种写法虽然形式上略有差别, 其实本质都是一样的, 只不过一个用了这个前缀和的下标0 ,一个没有用下标0 ,只是用了下标1, 严格来说这不算各个问题, 可谁让我一直心里过意不去呢, 所以我必须弄清楚他.

从1开始的优势

直接和原数组对仗, 也就是下标相互对应, 因此后续遍历使用的时候直接对应使用即可, 但是要注意当i -1 出现的时候要处理越界的情况

就比如一个例子: 当你计算完了前缀和需要遍历所有区间然后统计区间内和为k的区间有多少个,你会怎么处理?

一个最简单暴力的方式: 两层for循环, 我们可以比较一下, 如果此时你用的是

从0开始的前缀和数组

java 复制代码

	static int solve1_1(int[] a,int k) {
		int n = a.length;
		int[] sum = new int[n];
		sum[0] =a[0];
		
		for(int i=1;i<n;i++) {
			sum[i]=sum[i-1]+a[i];
		}
		
		int count =0;
		for(int i=0;i< n;i++) {
			for(int j =i;j<n;j++) {
				//根据公式: i-j 的区间和等于sum[j] - sum[i-1]
				//此时必须特殊讨论i-1越界的情况
				int tmp = 0;
				if(i ==0)tmp = sum[j];
				else tmp = sum[j] - sum[i-1];
				if(tmp == k)count++;
			}
		}
		return count;
	}

从1开始的前缀和数组

java 复制代码

	static int solve2_1(int[] a,int k) {
		int n = a.length;
		int[] sum = new int[n+1];
		
		for(int i=1;i<n+1;i++) {
			sum[i]=sum[i-1]+a[i-1];
		}
		int count =0;
		for(int i= 1;i<=n ;i++) {
			for(int j =i;j<=n;j++) {
				//由于此时下表是从1开始, 假设一下此时i最小也就是1了, 如果i=1,那大不了sum[i-1]==0了
				//既越不了界也方便我们使用,可谓是一举两得
				int tmp = sum[j] - sum[i-1];
				if(tmp == k) count++;
			}
		}
		return count;
	}

对于另一些场景, 比如: 我们通常需要在读入数据的时候就将所有的前缀和计算好, 我们可以对比一下使用0和使用1的区别

使用0开始的前缀和数组

java 复制代码

static void solve1_2() {
		Scanner in = new Scanner(System.in);
		int n = in.nextInt();
		int[] b = new int[n];
		//除非你手动的从1开始,不然肯定会多一个判断条件,逃不掉的,因为你必须要处理越界
		for(int i =0;i<n;i++) {
			if(i ==0) b[i] = in.nextInt();
			else b[i] = b[i-1]+in.nextInt();
		}
	}

使用1开始的前缀和数组

java 复制代码

static void solve2_2() {
		Scanner in = new Scanner(System.in);
		int n = in.nextInt();
		int[] b = new int[n+1];
		//如果使用1下标开始,就不用考虑越界的情况
		for(int i =1;i<= n;i++) {
			b[i] = b[i-1]+in.nextInt();
		}
	}

总结

总之以上例子并没有说从0下标开始是错的, 只是对比了两者的这个优势和劣势, 其实, 实际运用的时候你是需要实际的场景去做的.

但是客观上来讲, 这个使用1开始确实他就比从0开始要优雅简洁一点, 这只是一个小建议, 所有今后在使用的时候还是使用1开始可能会更加方便, 优雅.

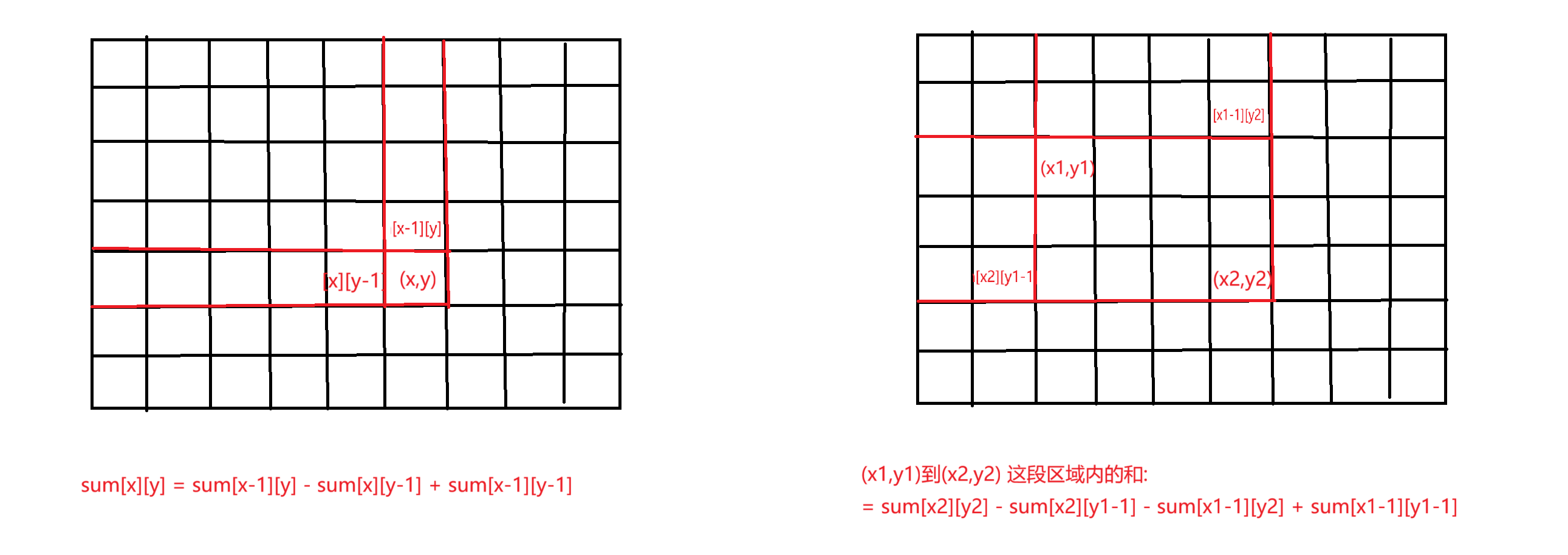
二维

这个二维, 在实战中直接实时画图回忆就行了, 不要死记公式, 容易记错, 只要抓到他的思想, 什么时候都能推导出来.

对于二维一般就是从[1,1] 下标开始了, 因此这里毋庸置疑, 直接使用即可