LeetCode 20/155/394/739/84/42/单调栈核心原理与经典题型全解析

目录

一、单调栈核心概念与原理

[1. 定义](#1. 定义)

[2. 常见类型与适用场景](#2. 常见类型与适用场景)

[3. 核心原理可视化](#3. 核心原理可视化)

二、经典栈题型全解析

[题型 1：有效的括号（LeetCode 20）------ 栈解决「匹配问题」](#题型 1：有效的括号（LeetCode 20）—— 栈解决「匹配问题」)

题目描述

思路分析

[重难点 / 易错点](#重难点 / 易错点)

[Java 实现（多解）](#Java 实现（多解）)

解题技巧

[题型 2：最小栈（LeetCode 155）------ 辅助栈存「当前最小值」](#题型 2：最小栈（LeetCode 155）—— 辅助栈存「当前最小值」)

题目描述

思路分析

[重难点 / 易错点](#重难点 / 易错点)

[Java 实现（多解）](#Java 实现（多解）)

解题技巧

[题型 3：字符串解码（LeetCode 394）------ 双栈处理「嵌套结构」](#题型 3：字符串解码（LeetCode 394）—— 双栈处理「嵌套结构」)

题目描述

思路分析

[重难点 / 易错点](#重难点 / 易错点)

[Java 实现（多解）](#Java 实现（多解）)

解题技巧

[题型 4：每日温度（LeetCode 739）------ 单调栈找「下一个更大元素」](#题型 4：每日温度（LeetCode 739）—— 单调栈找「下一个更大元素」)

题目描述

思路分析

[重难点 / 易错点](#重难点 / 易错点)

[Java 实现（多解）](#Java 实现（多解）)

解题技巧

[题型 5：柱状图中最大的矩形（LeetCode 84）------ 单调栈找「左右边界」](#题型 5：柱状图中最大的矩形（LeetCode 84）—— 单调栈找「左右边界」)

题目描述

思路分析

[重难点 / 易错点](#重难点 / 易错点)

[Java 实现（多解）](#Java 实现（多解）)

解题技巧

[题型 6：接雨水（LeetCode 42）------ 单调栈找「凹槽边界」](#题型 6：接雨水（LeetCode 42）—— 单调栈找「凹槽边界」)

题目描述

思路分析

[重难点 / 易错点](#重难点 / 易错点)

[Java 实现（多解）](#Java 实现（多解）)

解题技巧

三、核心总结

[1. 栈题型核心分类与技巧](#1. 栈题型核心分类与技巧)

[2. 避坑指南](#2. 避坑指南)

[3. 单调性选择口诀](#3. 单调性选择口诀)

---

本次总结完整覆盖基础栈应用 （有效括号、最小栈、字符串解码）和单调栈进阶应用（每日温度、柱状图最大矩形、接雨水），每道题均包含「思路分析、重难点、多解法实现、解题技巧」，帮你从基础到进阶吃透栈的核心用法。

一、单调栈核心概念与原理

1. 定义

单调栈是一种维护栈内元素单调性的特殊栈结构：栈内元素从栈底到栈顶始终保持「严格 / 非严格递增」或「严格 / 非严格递减」。

• 核心操作：新元素入栈前，循环弹出所有破坏当前单调性的栈顶元素，直到栈满足单调性，再将新元素入栈。
• 本质：用栈记录「元素的邻域关系」，将暴力解法中「重复的比较逻辑」通过栈一次性记录，实现时间复杂度从 O(n2) 优化到 O(n)（每个元素仅入栈、出栈各一次）。

2. 常见类型与适用场景

单调栈类型	核心特征	典型应用场景
单调递减栈	栈底 → 栈顶：元素值递减	找「下一个更大元素」（如每日温度）、接雨水
单调递增栈	栈底 → 栈顶：元素值递增	找「左右第一个更小元素」（如柱状图最大矩形）

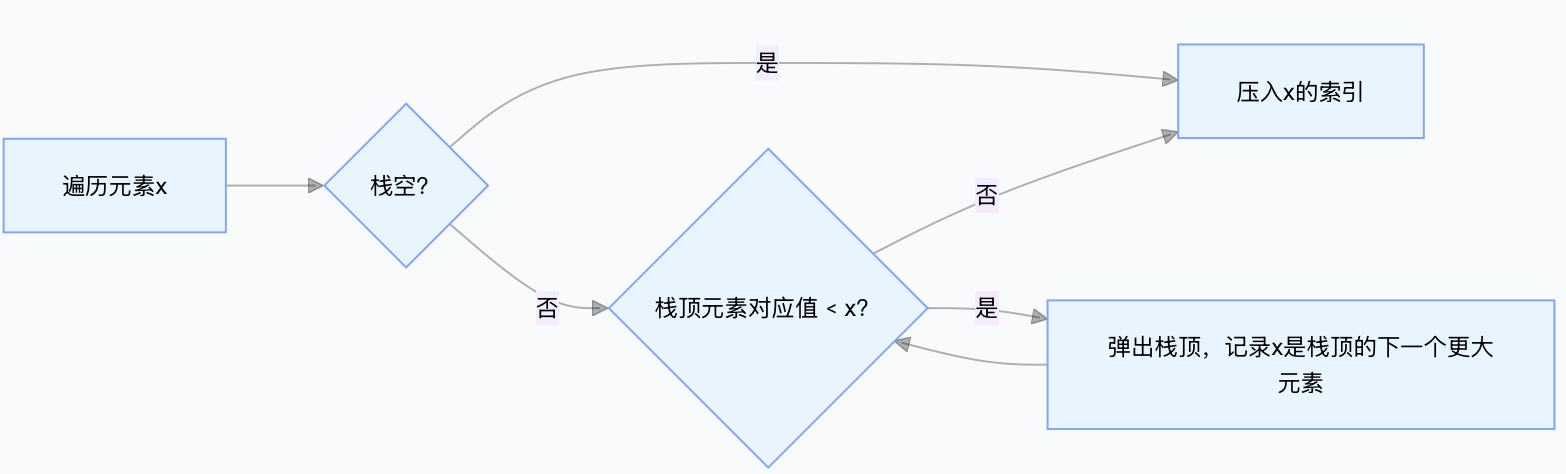
3. 核心原理可视化

以「单调递减栈找下一个更大元素」为例：

二、经典栈题型全解析

题型 1：有效的括号（LeetCode 20）------ 栈解决「匹配问题」

题目描述

给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串 s ，判断字符串是否有效。有效字符串需满足：

1. 左括号必须用相同类型的右括号闭合；
2. 左括号必须以正确的顺序闭合；
3. 每个右括号都有一个对应的相同类型的左括号。

思路分析

解法	思路	时间复杂度	空间复杂度
暴力替换	循环替换成对的括号（如"()"→""），直到无法替换，最终字符串为空则有效	O(n2)	O(1)（原地替换）
栈 + 哈希表	1. 哈希表存储「右括号→左括号」的映射（简化匹配判断）；2. 遍历字符串：- 左括号入栈；- 右括号则检查栈顶是否匹配，不匹配直接返回 false，匹配则弹出栈顶；3. 最终栈空则有效（避免左括号多余）	O(n)	O(n)

重难点 / 易错点

1. 哈希表映射方向：新手易搞反（存左→右），导致右括号匹配时需要遍历判断，效率低；
2. 栈空判断：遇到右括号时，若栈空直接返回 false（避免右括号多余）；
3. 最终栈空：遍历结束后栈非空（左括号多余），也是无效的，新手易遗漏此判断。

Java 实现（多解）

// 解法1：暴力替换（易理解但效率低）
public boolean isValid_brute(String s) {
    while (s.contains("()") || s.contains("[]") || s.contains("{}")) {
        s = s.replace("()", "").replace("[]", "").replace("{}", "");
    }
    return s.isEmpty();
}

// 解法2：栈 + 哈希表（最优解）
public boolean isValid_stack(String s) {
    // 哈希表：右括号 → 左括号（核心，快速匹配）
    Map<Character, Character> map = new HashMap<>();
    map.put(')', '(');
    map.put(']', '[');
    map.put('}', '{');
    
    Deque<Character> stack = new LinkedList<>();
    for (char c : s.toCharArray()) {
        if (map.containsKey(c)) { // 当前是右括号
            // 栈空 或 栈顶不匹配 → 无效
            if (stack.isEmpty() || stack.pop() != map.get(c)) {
                return false;
            }
        } else { // 当前是左括号，入栈
            stack.push(c);
        }
    }
    // 栈空才有效（避免左括号多余）
    return stack.isEmpty();
}

解题技巧

1. 哈希表预存映射是关键，把「多条件判断」简化为「一次哈希查找」；
2. 可优化：用数组替代哈希表（因为括号类型固定），效率更高（char 的 ASCII 码作为索引）；
3. 特殊用例：空字符串（有效）、单括号（无效）、嵌套括号（如"([{}])"）需重点测试。

---

题型 2：最小栈（LeetCode 155）------ 辅助栈存「当前最小值」

题目描述

设计一个支持 push ，pop ，top 操作，并能在常数时间内检索到最小元素的栈。实现 MinStack 类:

• MinStack() 初始化堆栈对象；
• void push(int val) 将元素 val 推入堆栈；
• void pop() 删除堆栈顶部的元素；
• int top() 获取堆栈顶部的元素；
• int getMin() 检索堆栈中的最小元素。

思路分析

解法	思路	时间复杂度	空间复杂度
辅助栈（同步）	1. 主栈存所有元素；2. 辅助栈存「当前栈的最小值」（push 时压入 min (当前值，辅助栈顶)，pop 时同步弹出）；3. getMin 直接取辅助栈顶	O(1)（所有操作）	O(n)
辅助栈（非同步）	仅当新元素≤辅助栈顶时才压入辅助栈，pop 时若主栈顶 = 辅助栈顶才弹出辅助栈	O(1)（所有操作）	O(n)（最坏），平均更优
单栈存差值	栈存「当前值 - 最小值」，通过差值还原原值和最小值，节省空间	O(1)（所有操作）	O(1)（仅存最小值变量）

重难点 / 易错点

1. 辅助栈同步性：新手易忘记 pop 时同步弹出辅助栈，导致 getMin 错误；
2. 空栈处理：push 第一个元素时，辅助栈需压入该元素（无栈顶可比较）；
3. 非同步辅助栈的条件：必须是≤而非 <（避免重复最小值被弹出后辅助栈无对应值）。

Java 实现（多解）

// 解法1：同步辅助栈（最易理解，推荐新手）
class MinStack {
    private Deque<Integer> mainStack; // 主栈：存所有元素
    private Deque<Integer> minStack;  // 辅助栈：存当前最小值

    public MinStack() {
        mainStack = new LinkedList<>();
        minStack = new LinkedList<>();
    }

    public void push(int val) {
        mainStack.push(val);
        // 辅助栈压入当前最小值（栈空则压入val，否则压入min(val, 辅助栈顶)）
        int minVal = minStack.isEmpty() ? val : Math.min(val, minStack.peek());
        minStack.push(minVal);
    }

    public void pop() {
        // 同步弹出，保证辅助栈和主栈长度一致
        mainStack.pop();
        minStack.pop();
    }

    public int top() {
        return mainStack.peek();
    }

    public int getMin() {
        return minStack.peek();
    }
}

// 解法2：非同步辅助栈（节省空间）
class MinStack_optimized {
    private Deque<Integer> mainStack;
    private Deque<Integer> minStack;

    public MinStack_optimized() {
        mainStack = new LinkedList<>();
        minStack = new LinkedList<>();
    }

    public void push(int val) {
        mainStack.push(val);
        // 仅当val≤辅助栈顶时才压入（避免重复存储）
        if (minStack.isEmpty() || val <= minStack.peek()) {
            minStack.push(val);
        }
    }

    public void pop() {
        // 仅当主栈顶=辅助栈顶时，才弹出辅助栈
        if (mainStack.peek().equals(minStack.peek())) {
            minStack.pop();
        }
        mainStack.pop();
    }

    public int top() {
        return mainStack.peek();
    }

    public int getMin() {
        return minStack.peek();
    }
}

// 解法3：单栈存差值（空间最优，理解稍难）
class MinStack_single {
    private Deque<Long> stack; // 存差值：当前值 - 最小值（用long避免溢出）
    private long minVal;       // 记录当前最小值

    public MinStack_single() {
        stack = new LinkedList<>();
    }

    public void push(int val) {
        if (stack.isEmpty()) {
            minVal = val;
            stack.push(0L); // 差值为0
        } else {
            long diff = val - minVal;
            stack.push(diff);
            // 更新最小值（diff<0说明val更小）
            if (diff < 0) {
                minVal = val;
            }
        }
    }

    public void pop() {
        long diff = stack.pop();
        // 差值<0说明弹出的是最小值，需要还原之前的最小值
        if (diff < 0) {
            minVal = minVal - diff;
        }
    }

    public int top() {
        long diff = stack.peek();
        // 差值≥0：当前值 = 最小值 + 差值；差值<0：当前值就是最小值
        return diff >= 0 ? (int) (minVal + diff) : (int) minVal;
    }

    public int getMin() {
        return (int) minVal;
    }
}

解题技巧

1. 新手优先掌握「同步辅助栈」，逻辑最简单，不易出错；
2. 单栈存差值需注意溢出问题（用 long 存储差值）；
3. 边界测试：连续 push 相同最小值、push 递减序列、pop 最小值后 getMin 是否正确。

---

题型 3：字符串解码（LeetCode 394）------ 双栈处理「嵌套结构」

题目描述

给定一个经过编码的字符串，返回它解码后的字符串。编码规则为: k[encoded_string]，表示其中方括号内部的 encoded_string 正好重复 k 次。注意 k 保证为正整数。例如：输入 "3[a]2[bc]" → 输出 "aaabcbc"；输入 "3[a2[bc]]" → 输出 "abcbcabcbcabcbc"。

思路分析

解法	思路	时间复杂度	空间复杂度
双栈（数字 + 字符串）	1. 数字栈存重复次数，字符串栈存「[」前的临时字符串；2. 遍历字符：- 数字：累积计算（处理多位数）；- '['：压栈并重置临时变量；- ']'：弹栈拼接（临时字符串 × 重复次数）；- 普通字符：拼接临时字符串	O(n)（最终字符串长度）	O(n)
递归	遇到 '[' 递归处理括号内的字符串，返回解码结果后重复 k 次，拼接外层字符串	O(n)	O(n)（递归栈）

重难点 / 易错点

1. 多位数处理 ：新手易把数字字符单独处理（如"123"拆成 1、2、3），需用num = num*10 + (c-'0')累积；
2. 嵌套处理：双栈的核心是「分层存储」，遇到 ']' 时只处理最近的一层，新手易混淆多层嵌套的拼接顺序；
3. 临时变量重置：遇到 '[' 时必须重置 currStr 和 num，否则会拼接上一层的内容。

Java 实现（多解）

// 解法1：双栈（最优解，迭代）
public String decodeString_stack(String s) {
    Deque<Integer> numStack = new LinkedList<>(); // 存重复次数
    Deque<String> strStack = new LinkedList<>();  // 存[前的临时字符串
    StringBuilder currStr = new StringBuilder();  // 当前拼接的字符串
    int num = 0; // 当前解析的数字（处理多位数）
    
    for (char c : s.toCharArray()) {
        if (Character.isDigit(c)) {
            // 处理多位数：如"123" → 1*10+2=12 → 12*10+3=123
            num = num * 10 + (c - '0');
        } else if (c == '[') {
            // 压栈：保存当前数字和字符串，准备处理括号内内容
            numStack.push(num);
            strStack.push(currStr.toString());
            // 重置：开始拼接括号内的字符串
            currStr = new StringBuilder();
            num = 0;
        } else if (c == ']') {
            // 弹栈：取出重复次数和[前的字符串
            int repeat = numStack.pop();
            String prevStr = strStack.pop();
            // 拼接：prevStr + currStr重复repeat次
            StringBuilder temp = new StringBuilder(prevStr);
            for (int i = 0; i < repeat; i++) {
                temp.append(currStr);
            }
            // 更新currStr，继续处理外层
            currStr = temp;
        } else {
            // 普通字符，直接拼接
            currStr.append(c);
        }
    }
    return currStr.toString();
}

// 解法2：递归（更简洁，适合理解嵌套）
private int index = 0; // 全局索引，记录当前遍历位置
public String decodeString_recursion(String s) {
    StringBuilder res = new StringBuilder();
    int num = 0;
    while (index < s.length()) {
        char c = s.charAt(index);
        if (Character.isDigit(c)) {
            num = num * 10 + (c - '0');
            index++;
        } else if (c == '[') {
            index++; // 跳过[，进入递归处理括号内
            String sub = decodeString_recursion(s);
            // 重复num次
            for (int i = 0; i < num; i++) {
                res.append(sub);
            }
            num = 0; // 重置数字
        } else if (c == ']') {
            index++; // 跳过]，返回当前层结果
            return res.toString();
        } else {
            res.append(c);
            index++;
        }
    }
    return res.toString();
}

解题技巧

1. 双栈的核心是「分层」：每遇到一个 '[' 就分层，']' 就合并当前层，完美处理嵌套；
2. 递归解法的关键是「全局索引」：避免递归调用时重复遍历字符；
3. 测试用例优先选嵌套案例（如"3[a2[bc]]"），验证分层拼接是否正确。

---

题型 4：每日温度（LeetCode 739）------ 单调栈找「下一个更大元素」

题目描述

给定一个整数数组 temperatures，表示每天的温度，返回一个数组 answer，其中 answer[i] 是指对于第 i 天，下一个更高温度出现在几天后。如果气温在这之后都不会升高，请在该位置用 0 代替。

思路分析

解法	思路	时间复杂度	空间复杂度
暴力解法	遍历每个元素，向后找第一个更大的温度，记录天数差	O(n2)	O(1)
单调递减栈	栈存「温度索引」（而非值，方便计算天数差），遍历数组时：1. 若当前温度 > 栈顶索引温度 → 弹出栈顶，计算天数差；2. 否则压入当前索引	O(n)	O(n)

重难点 / 易错点

1. 栈存索引而非值：新手易直接存温度值，导致无法计算「天数差」（索引差）；
2. 剩余元素处理：遍历结束后栈中未弹出的索引，对应「无更高温度」，结果默认 0（无需额外处理）；
3. 单调性方向 ：找「下一个更大元素」用递减栈（栈顶是最近的更小 / 相等元素），新手易搞反成递增栈。

Java 实现（多解）

// 解法1：暴力解法
public int[] dailyTemperatures_brute(int[] temperatures) {
    int n = temperatures.length;
    int[] res = new int[n];
    for (int i = 0; i < n; i++) {
        for (int j = i + 1; j < n; j++) {
            if (temperatures[j] > temperatures[i]) {
                res[i] = j - i;
                break; // 找到第一个更大的就退出
            }
        }
    }
    return res;
}

// 解法2：单调递减栈（最优解）
public int[] dailyTemperatures_stack(int[] temperatures) {
    int n = temperatures.length;
    int[] res = new int[n];
    Deque<Integer> stack = new LinkedList<>(); // 存索引，单调递减栈
    
    for (int i = 0; i < n; i++) {
        // 核心：当前温度 > 栈顶索引温度 → 弹出栈顶，计算天数差
        while (!stack.isEmpty() && temperatures[i] > temperatures[stack.peek()]) {
            int prevIdx = stack.pop(); // 弹出的索引是需要计算结果的位置
            res[prevIdx] = i - prevIdx; // 天数差 = 当前索引 - 弹出索引
        }
        // 满足递减性，压入当前索引
        stack.push(i);
    }
    // 栈中剩余索引的res默认是0，无需处理
    return res;
}

解题技巧

1. 栈中始终存「未找到下一个更大元素的索引」，遍历到更大元素时批量结算；
2. 若题目要求「下一个更小元素」，只需将判断条件改为 temperatures[i] < temperatures[stack.peek()]（仍用递减栈）。

---

题型 5：柱状图中最大的矩形（LeetCode 84）------ 单调栈找「左右边界」

题目描述

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1。求在该柱状图中，能够勾勒出来的矩形的最大面积。

思路分析

核心逻辑：每个柱子能构成的最大矩形 = 高度 × 左右延伸的最大宽度，宽度由「左右第一个更矮的柱子」决定。

解法	思路	时间复杂度	空间复杂度
暴力解法	遍历每个柱子，向左右找第一个更矮的柱子，计算宽度和面积	O(n2)	O(1)
单调递增栈	栈存「柱子索引」（递增栈），遍历到 n（设高度为 0）：1. 若当前高度 < 栈顶索引高度 → 弹出栈顶，计算该柱子的面积；2. 否则压入当前索引	O(n)	O(n)
哨兵优化栈	在原数组前后加「哨兵 0」，简化边界处理（无需遍历到 n，无需判断栈空）	O(n)	O(n)

重难点 / 易错点

1. 遍历到 n 的原因 ：数组最后一个元素的右边界可能未找到，设 i=n 且高度为 0（强制弹出栈中剩余元素）；
2. 宽度计算 ：width = right - left - 1（right是当前索引，left是弹出后新栈顶，栈空则为 - 1），新手易误算为 right - left；
3. 单调性方向 ：找「左右第一个更矮元素」用递增栈（栈顶是最近的更高 / 相等元素），与每日温度相反；
4. 栈空处理：弹出栈顶后栈空，说明该柱子左边无更矮元素，左边界为 - 1。

Java 实现（多解）

// 解法1：暴力解法
public int largestRectangleArea_brute(int[] heights) {
    int maxArea = 0;
    int n = heights.length;
    for (int i = 0; i < n; i++) {
        int h = heights[i];
        // 找左边界：左边第一个更矮的柱子
        int left = i;
        while (left > 0 && heights[left - 1] >= h) left--;
        // 找右边界：右边第一个更矮的柱子
        int right = i;
        while (right < n - 1 && heights[right + 1] >= h) right++;
        // 计算面积
        int width = right - left + 1;
        maxArea = Math.max(maxArea, h * width);
    }
    return maxArea;
}

// 解法2：单调递增栈（基础版）
public int largestRectangleArea_stack(int[] heights) {
    int maxArea = 0;
    int n = heights.length;
    Deque<Integer> stack = new LinkedList<>(); // 存索引，单调递增栈
    
    // 遍历到n（而非n-1），currH=0强制弹出剩余元素
    for (int i = 0; i <= n; i++) {
        int currH = (i == n) ? 0 : heights[i];
        
        // 核心：当前高度 < 栈顶索引高度 → 弹出栈顶计算面积
        while (!stack.isEmpty() && currH < heights[stack.peek()]) {
            int topIdx = stack.pop(); // 弹出的柱子索引
            int h = heights[topIdx];
            // 左边界：栈空则为-1，否则是新栈顶
            int left = stack.isEmpty() ? -1 : stack.peek();
            int right = i; // 右边界是当前索引
            int width = right - left - 1;
            maxArea = Math.max(maxArea, h * width);
        }
        stack.push(i);
    }
    return maxArea;
}

// 解法3：哨兵优化版（更简洁，无需处理栈空和i=n）
public int largestRectangleArea_sentinel(int[] heights) {
    int maxArea = 0;
    // 前后加哨兵0，简化边界处理
    int[] newHeights = new int[heights.length + 2];
    System.arraycopy(heights, 0, newHeights, 1, heights.length);
    Deque<Integer> stack = new LinkedList<>();
    
    for (int i = 0; i < newHeights.length; i++) {
        // 递增栈，当前高度 < 栈顶高度 → 弹出计算
        while (!stack.isEmpty() && newHeights[i] < newHeights[stack.peek()]) {
            int topIdx = stack.pop();
            int h = newHeights[topIdx];
            int width = i - stack.peek() - 1; // 哨兵保证栈不会空
            maxArea = Math.max(maxArea, h * width);
        }
        stack.push(i);
    }
    return maxArea;
}

解题技巧

1. 哨兵优化：前后加 0，避免「栈空判断」和「遍历到 n」的特殊处理，代码更简洁；
2. 面积结算时机：只有当「遇到更矮柱子」时才结算栈顶柱子的面积（因为此时左右边界已确定）；
3. 手推验证：新手必手推 [2,1,5,6,2,3] 示例，确认每一步栈的变化和面积计算。

---

题型 6：接雨水（LeetCode 42）------ 单调栈找「凹槽边界」

题目描述

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨后能接多少雨水。

思路分析

核心逻辑：每个位置能接的雨水量 = min (左最大高度，右最大高度) - 当前高度（高度差 > 0 才有效）。

解法	思路	时间复杂度	空间复杂度
暴力解法	遍历每个位置，找左右最大高度，计算雨水量	O(n2)	O(1)
动态规划	预处理左右最大高度数组，避免重复计算	O(n)	O(n)
单调递减栈	栈存「柱子索引」（递减栈），遇到更高柱子时，弹出栈顶形成「凹槽」，计算凹槽水量	O(n)	O(n)

重难点 / 易错点

1. 凹槽水量计算 ：水量 = 宽度 × 高度差，其中：
   • 宽度 = 当前索引 - 新栈顶索引 - 1；
   • 高度差 = min (当前高度，新栈顶高度) - 弹出元素高度；
2. 单调性方向 ：找「凹槽边界」用递减栈（栈顶是凹槽底部，新栈顶和当前索引是凹槽左右边界）；
3. 高度差取 min：新手易直接用「当前高度 - 弹出高度」，忽略左边界可能更低的情况。

Java 实现（多解）

// 解法1：暴力解法
public int trap_brute(int[] height) {
    int res = 0;
    int n = height.length;
    for (int i = 1; i < n - 1; i++) { // 首尾无法接水
        // 找左最大高度
        int leftMax = 0;
        for (int j = i; j >= 0; j--) leftMax = Math.max(leftMax, height[j]);
        // 找右最大高度
        int rightMax = 0;
        for (int j = i; j < n; j++) rightMax = Math.max(rightMax, height[j]);
        // 计算当前位置雨水量
        res += Math.min(leftMax, rightMax) - height[i];
    }
    return res;
}

// 解法2：动态规划
public int trap_dp(int[] height) {
    if (height.length == 0) return 0;
    int res = 0;
    int n = height.length;
    int[] leftMax = new int[n]; // 左最大高度数组
    int[] rightMax = new int[n]; // 右最大高度数组
    
    // 预处理左最大高度
    leftMax[0] = height[0];
    for (int i = 1; i < n; i++) leftMax[i] = Math.max(leftMax[i-1], height[i]);
    // 预处理右最大高度
    rightMax[n-1] = height[n-1];
    for (int i = n-2; i >= 0; i--) rightMax[i] = Math.max(rightMax[i+1], height[i]);
    // 计算总雨水量
    for (int i = 0; i < n; i++) {
        res += Math.min(leftMax[i], rightMax[i]) - height[i];
    }
    return res;
}

// 解法3：单调递减栈（最优解）
public int trap_stack(int[] height) {
    int res = 0;
    Deque<Integer> stack = new LinkedList<>(); // 存索引，单调递减栈
    
    for (int i = 0; i < height.length; i++) {
        // 核心：当前高度 > 栈顶索引高度 → 弹出栈顶，计算凹槽水量
        while (!stack.isEmpty() && height[i] > height[stack.peek()]) {
            int bottomIdx = stack.pop(); // 凹槽底部索引
            if (stack.isEmpty()) break; // 无左边界，无法接水
            // 凹槽左边界索引
            int leftIdx = stack.peek();
            // 凹槽宽度
            int width = i - leftIdx - 1;
            // 凹槽有效高度（取左右边界的较小值 - 底部高度）
            int h = Math.min(height[i], height[leftIdx]) - height[bottomIdx];
            res += width * h;
        }
        stack.push(i);
    }
    return res;
}

解题技巧

1. 单调栈接雨水的核心是「找凹槽」：栈顶是凹槽底，新栈顶是左边界，当前索引是右边界；
2. 动态规划预处理数组时，注意「从左到右算左最大」「从右到左算右最大」；
3. 首尾元素无需计算（无法形成凹槽），可跳过优化性能。

三、核心总结

1. 栈题型核心分类与技巧

题型	核心解法	单调性 / 辅助栈类型	核心目标	关键注意点
有效括号	栈 + 哈希表	普通栈	括号匹配	哈希表存「右→左」，最终栈需空
最小栈	辅助栈 / 单栈	辅助栈（同步 / 非同步）	O (1) 找最小值	辅助栈需同步弹出，非同步用≤
字符串解码	双栈（数字 + 字符串）	普通栈	处理嵌套解码	多位数累积计算，分层压栈 / 弹栈
每日温度	单调栈	单调递减栈	找下一个更大元素的索引差	栈存索引，剩余元素结果为 0
柱状图最大矩形	单调栈	单调递增栈	找左右第一个更小元素的边界	遍历到 n / 加哨兵，宽度 = 右 - 左 - 1
接雨水	单调栈 / 动态规划	单调递减栈	找凹槽的左右边界	水量 = 宽度 ×(min (左右高)- 底高)

2. 避坑指南

1. 不要死记代码，先理解「栈的核心作用」：✅ 普通栈：处理「匹配、嵌套」（括号、解码）；✅ 辅助栈：扩展栈的功能（最小栈）；✅ 单调栈：优化「邻域边界查找」（每日温度、柱状图、接雨水）；
2. 栈存「索引」而非「值」：几乎所有需要计算「距离 / 宽度」的场景，索引比值更有用；
3. 手推示例是关键：每道题至少手推 1 个示例（如 [2,1,5,6,2,3]），明确栈的变化和结算时机。

3. 单调性选择口诀

• 找「下一个更大元素 / 凹槽」→ 用单调递减栈；
• 找「左右第一个更小元素」→ 用单调递增栈。

---