数据结构 之 【图的最短路径】(Dijstra、BellmanFord、FloydWarShall算法实现)

zl_dfq2025-10-03 9:14

目录

1.最短路径

1.1单源最短路径--Dijstra算法

代码实现

完整呈现

1.2打印最短路径的算法

1.3单源最短路径--Bellman-Ford算法

代码实现

完整呈现

1.4多源最短路径--Floyd-Warshall算法

代码实现

完整呈现

2.总结

下述算法均是在邻接表实现图的基础上实现的，参考我的往期博客

1.最短路径

最短路径问题：从在带权有向图G 中的某一顶点出发 ，找出一条通往另一顶点 的最短路径，最短也就是沿路径各边的权值总和达到最小

1.1单源最短路径--Dijstra算法

  • 单源最短路径问题：给定一个图G = ( V ， E )，求源结点s ∈ V到 图 中每个结点v ∈ V 的最短路径
  • 算法思路：将顶点分为S、Q两个集合，S中存放最短路径中的顶点，Q存放尚未确定的顶点。每次从Q中找出一个从源节点到该点代价最小的顶点，将其放入S中，然后对其相邻节点进行松弛操作，反复进行找点、放入、松弛操作，直到所有顶点都进入S为止。至于一些起点到达不了的结点在算法循环后其代价仍为初始设定 的值，不发生变化
  • 松弛操作：（ 称找到的顶点为u ）将源点s通过该顶点u再到其相邻顶点v的权值和newSum与之前源点s到该相邻顶点v的权值和oldSum进行比较 ，如果newSum < oldSum 就更新oldSum为newSum 否则oldSum不变
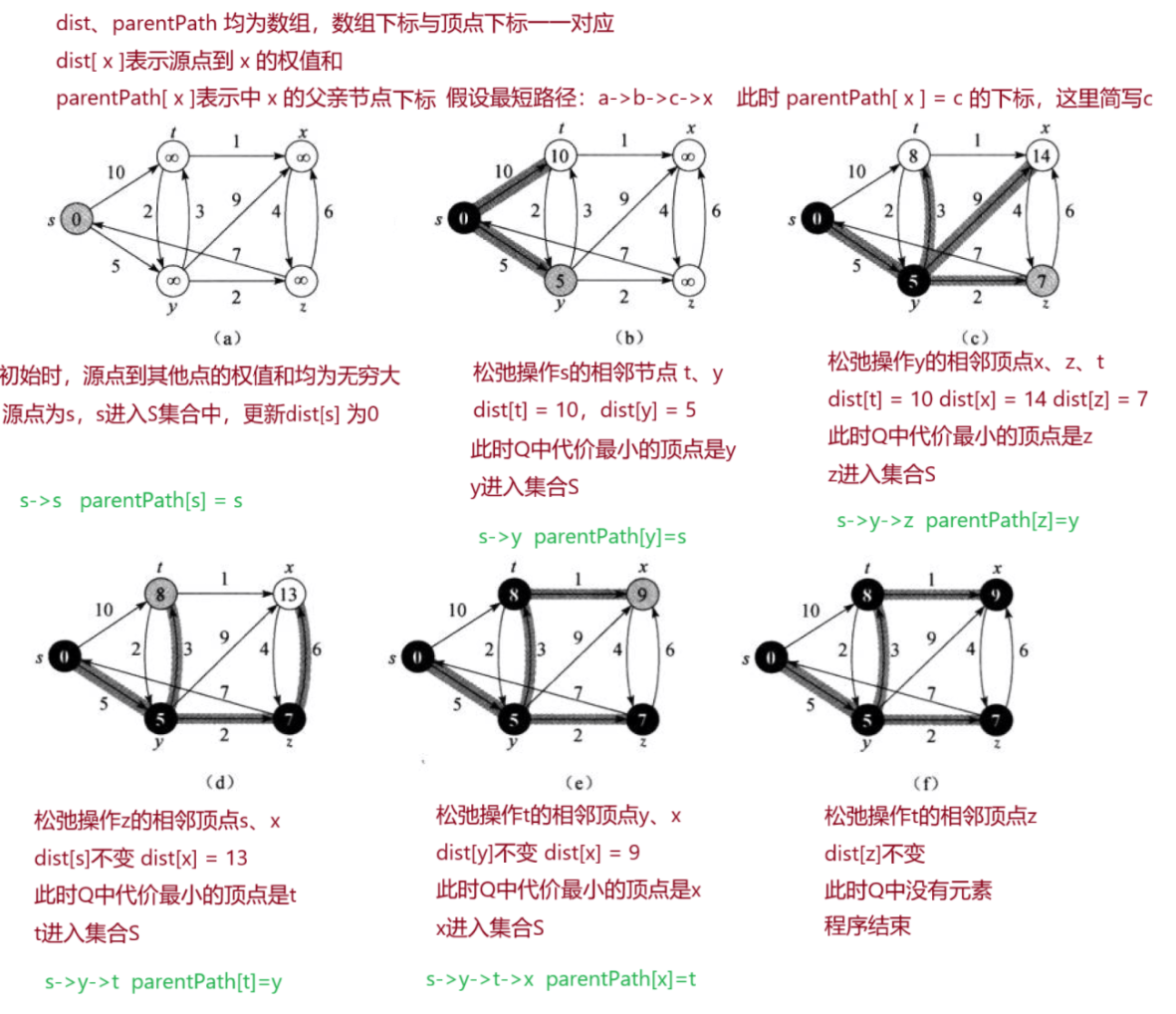
  • 算法要求：要求有向图， 且图中所有边的权重非负
  • 算法存在的问题：不支持图中带负权路径，如果带有负权路径，则可能会找不到一些路 径的最短路径
  • Dijkstra算法每次都是选择Q中最小的路径节点来进行更新，并加入S中，所以该算法使用的是贪心策略

代码实现

复制代码 
void Dijkstra(const V& src, vector<W>& dist, vector<int>& pPath)
{
	int n = _vertexes.size();
	int srci = GetIndexOfVertexes(src);
	dist.resize(n, W_MAX);
	pPath.resize(n, -1);
	dist[srci] = W();//最短路径长度
	pPath[srci] = srci;//父亲节点
	//分为两个集合S、Q，从Q中寻找代价最小的顶点u，然后进行松弛操作
	vector<bool> in(n, false);
    //从Q中选顶点
}

(1)顶点个数n、源点下标srci

(2)初始化源点到其他顶点的权值和为权值类型的最大值，

各个顶点的父亲节点下标初始化为-1

(3)使用bool数组区别S、Q中的顶点：

顶点在S中，顶点下标对应值为true

复制代码 
//一次选一个顶点，选n次
for(int k = 0; k < n; ++k)
{
	//找到了代价最小的顶点u
	W min = W_MAX;
	int u = srci;
	bool flag = false;
	for (int i = 0; i < n; ++i)
	{	//在Q中
		if (in[i] == false && dist[i] < min)
		{
			flag = true;
			min = dist[i];
			u = i;
		}
	}
	if (flag == false)
	{
		reutrn;
	}

	in[u] = true;//找到了就进入S
	//向外进行松弛操作 srci -> u u ->v 与 srci -> v
	for (int v = 0; v < n; ++v)
	{
		if (_matrix[u][v] < 0) throw invalid_argument("无效参数");
		//v点在S中，dist[u] + _matrix[u][v] >= dist[v]
		if (in[v] == false && _matrix[u][v] != W_MAX &&
			dist[u] + _matrix[u][v] < dist[v])
		{
			dist[v] = dist[u] + _matrix[u][v];
			pPath[v] = u;
		}
	}
}

(1)最外层for循环表示（找点、进集合、松弛）操作的次数，图中有n个顶点，就进行n次

使得源点能够到达包括自己在内的所有顶点

(2)找点：这里没有用优先级队列，而是在dist数组中暴力查找Q中代价最小的顶点

使用 flag 作为标记，当不能从Q中找出代价最小的顶点时，说明源点已到达它所能到达的所有顶点了

(3)标记：in[u] = true;//找到了就进入S

(4)松弛操作：srci -> u u ->v 与 srci -> v两者的值进行比较更新

  • 存在负权直接抛异常
  • 如果不判断u的临近顶点(u可直接到达)v是否在S中，程序也能实现该算法。这是因为：如果v在S中，则dist[u] >= dist[v]（v是找点时代价最小的顶点），_matrix[u][v] >= 0，所以dist[u] + _matrix[u][v] >= dist[v]，dist[v]不更新 如果v不在S中，正常比较更新即可

(5)如果更新了，父亲节点下标就是u

完整呈现

复制代码 
void Dijkstra(const V& src, vector<W>& dist, vector<int>& pPath)
{
	int n = _vertexes.size();
	int srci = GetIndexOfVertexes(src);
	dist.resize(n, W_MAX);
	pPath.resize(n, -1);
	dist[srci] = W();//最短路径长度
	pPath[srci] = srci;//父亲节点
	//分为两个集合S、Q，从Q中寻找代价最小的顶点u，然后进行松弛操作
	vector<bool> in(n, false);
	//一次选一个顶点，选n次
	for(int k = 0; k < n; ++k)
	{
		//找到了代价最小的顶点u
		W min = W_MAX;
		int u = srci;
		bool flag = false;
		for (int i = 0; i < n; ++i)
		{	//在Q中
			if (in[i] == false && dist[i] < min)
			{
				flag = true;
				min = dist[i];
				u = i;
			}
		}
		if (flag == false)
		{
			cout << "整个图不是连通图" << endl;
		}

		in[u] = true;//找到了就进入S
		//向外进行松弛操作 srci -> u u ->v 与 srci -> v
		for (int v = 0; v < n; ++v)
		{
			if (_matrix[u][v] < 0) throw invalid_argument("无效参数");
			//v点在S中，dist[u] + _matrix[u][v] >= dist[v]
			if (in[v] == false && _matrix[u][v] != W_MAX &&
				dist[u] + _matrix[u][v] < dist[v])
			{
				dist[v] = dist[u] + _matrix[u][v];
				pPath[v] = u;
			}
		}
	}
}

1.2打印最短路径的算法

复制代码 
void PrintShortPath(const V& src, vector<W>& dist, vector<int>& pPath)
{
	int n = _vertexes.size();
	int srci = GetIndexOfVertexes(src);
	//遍历最短路径权值和数组的每个顶点，并打印其父亲节点
	for (int i = 0; i < n; ++i)
	{
		if (i == srci) continue;
		vector<int> path;
		path.push_back(i);
		int parenti = pPath[i];
		while (parenti != srci)//源点和源点连接的第一个顶点符合要求
		{
			path.push_back(parenti);
			parenti = pPath[parenti];
		}
		path.push_back(srci);
		//逆置一下
		reverse(path.begin(), path.end());
		for (auto e : path)
		{
			cout << _vertexes[e] << "->";
		}
		cout << dist[i] << endl;
	}
}

(1)得到顶点个数n、源点下标srci

(2)遍历dist数组，按数组顺序打印最短路径

(3)不打印源点到源点的路径

(4)path数组存放路径，因为pPath存放的是节点的父亲节点下标所以我们是逆着寻找路径

即a->b->c->d->e，我们是逆着往回走，e<-d<-c<-b<-a

寻找逻辑与并查集的查找逻辑类似，向上寻找

  • 首先 path 中存入当前点的下标 i ，然后判断当前点 i 对应的pPath数组元素是否源点下标，如果不是，数组元素进入path，迭代父亲节点下标，继续寻找，循环跳出后，当前节点是源点到达的第一个顶点，再将源点下标压入path，然后逆置一下数组元素，数组中存放的就是源点到该顶点的最短路径了

(5)打印最短路径及权值

1.3单源最短路径--Bellman-Ford算法

  • 算法思路：对于有n个顶点的有向图，进行n-1轮松弛操作。第K轮松弛操作：更新所有通过 k条边 从源点到达的节点的最短距离
  • 为什么是n-1轮松弛操作呢？ 对于有n个顶点的有向图，两点之间最多有n-1条边，n-1轮松弛操作就包含了两点之间的所有路径。
  • 负权环：某个回路的权值和为负数
  • 该算法可以检测负权环问题，对于有n个顶点的有向图，第n轮松弛操作如果有更新，那么图中就存在负权环。 这是因为对于有n个顶点的有向图，两点之间最多有n-1条边，如果经过n条边 还可到达，只能说明两点之间存在环
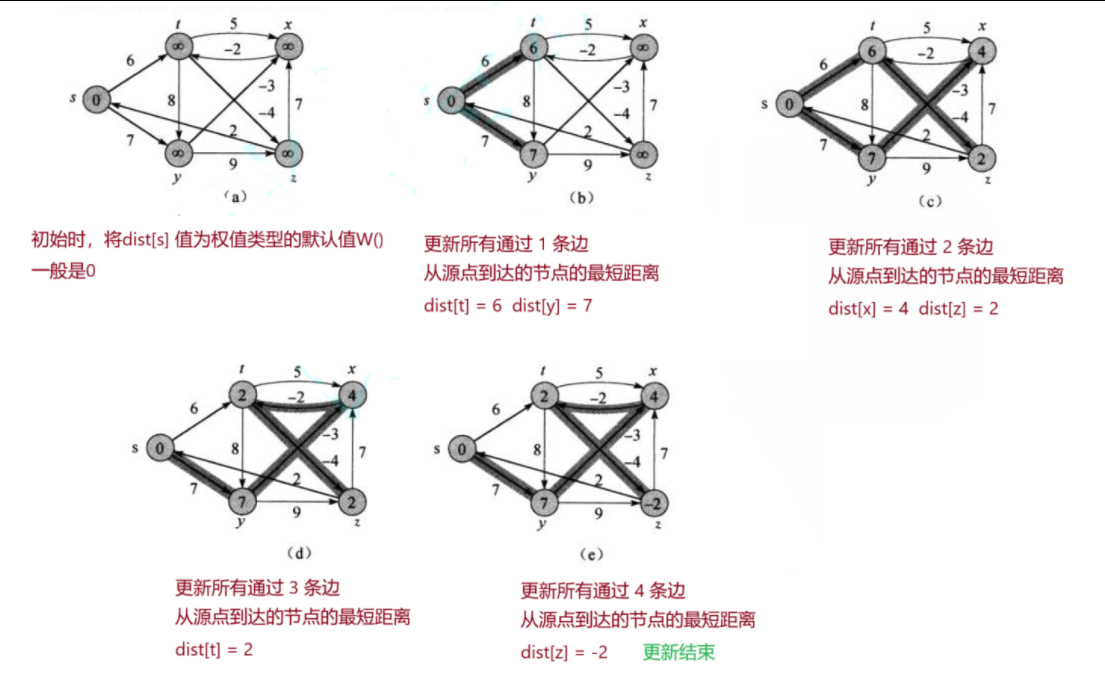
  • BellmanFord就是暴力查找更新，将源点到其他顶点的所有路径都列举比较，但效率就下降了。时间复杂度 O(N^3) 优化策略这里就略过了

代码实现

复制代码 
bool BellmanFord(const V& src, vector<W>& dist, vector<int>& pPath)
{
	int n = _vertexes.size();
	int srci = GetIndexOfVertexes(src);
	dist.resize(n, W_MAX);
	pPath.resize(n, -1);
	dist[srci] = W();
	pPath[srci] = srci;
    //松弛更新
}

(1)顶点个数n、源点下标srci

(2)更新dist、pPath数组，与Dijstra算法实现一致

复制代码 
for(int k = 0; k < n - 1; ++k)
{
	bool update = false;
	//从当前最短路径顶点松弛操作相邻顶点
	for (int i = 0; i < n; ++i)
	{
		for (int j = 0; j < n; ++j)
		{
            //源点不能到i，直接跳出循环
			if (dist[i] == W_MAX) break;
			//srci -> i i -> j srci -> j
			if (_matrix[i][j] != W_MAX && dist[i] + _matrix[i][j] < dist[j])
			{
				update = true;
				dist[j] = dist[i] + _matrix[i][j];
				pPath[j] = i;
			}
		}
	}
	if (update == false) return true;
}

(1)最外层循环表示进行 n-1 轮松弛更新

(2) 使用邻接矩阵，遍历存在的边(使用邻接表效率更高)

如果源点到顶点 i 的最短路径存在，并且 i 、j 相连有边，比较更新

(3)update变量作为标志位，n-1轮松弛更新中，有一次没有进行更新操作就说明

所有最短路径都已找到

复制代码 
			//第n轮松弛更新了，则存在环
			for (int i = 0; i < n; ++i)
			{
				for (int j = 0; j < n; ++j)
				{
					if (dist[i] == W_MAX) break;
					//srci -> i i -> j srci -> j
					if (_matrix[i][j] != W_MAX && dist[i] + _matrix[i][j] < dist[j])
					{
						return false;
						dist[j] = dist[i] + _matrix[i][j];
						pPath[j] = i;
					}
				}
			}

完整呈现

复制代码 
bool BellmanFord(const V& src, vector<W>& dist, vector<int>& pPath)
{
	int n = _vertexes.size();
	int srci = GetIndexOfVertexes(src);
	dist.resize(n, W_MAX);
	pPath.resize(n, -1);
	dist[srci] = W();
	pPath[srci] = srci;

	//一次松弛操作最多更新一个长度，n个顶点最多需要n-1次操作
	//更新所有通过 k条边 从源点到达的节点的最短距离
	for(int k = 0; k < n - 1; ++k)
	{
		bool update = false;
		//从当前最短路径顶点松弛操作相邻顶点
		for (int i = 0; i < n; ++i)
		{
			for (int j = 0; j < n; ++j)
			{
				if (dist[i] == W_MAX) break;
				//srci -> i i -> j srci -> j
				if (_matrix[i][j] != W_MAX && dist[i] + _matrix[i][j] < dist[j])
				{
					update = true;
					dist[j] = dist[i] + _matrix[i][j];
					pPath[j] = i;
				}
			}
		}
		if (update == false) return true;
	}
	//第n轮松弛更新，则存在环
	for (int i = 0; i < n; ++i)
	{
		for (int j = 0; j < n; ++j)
		{
			if (dist[i] == W_MAX) break;
			//srci -> i i -> j srci -> j
			if (_matrix[i][j] != W_MAX && dist[i] + _matrix[i][j] < dist[j])
			{
				return false;
				dist[j] = dist[i] + _matrix[i][j];
				pPath[j] = i;
			}
		}
	}
    //不更新，不存在环
	return true;
}

1.4多源最短路径--Floyd-Warshall算法

  • 该算法解决的是任意两点间的最短路径
  • 算法思路：任一两点之间要么直接相连，要么间接相连，所以通过三重循环（k, i, j），逐步考虑中间顶点k，更新所有顶点对(i,j)的距离

代码实现

复制代码 
bool FloydWarShall(vector<vector<W>>& vvDist, vector<vector<int>>& vvpPath)
{
	int n = _vertexes.size();
	vvDist.resize(n, vector<W>(n, W_MAX));
	vvpPath.resize(n, vector<int>(n, -1));
	//初始化通过一条边直接相连接的顶点
	for (int i = 0; i < n; ++i)
	{
		for (int j = 0; j < n; ++j)
		{
			if (_matrix[i][j] != W_MAX)
			{
				vvDist[i][j] = _matrix[i][j];
				vvpPath[i][j] = i;
			}

			if (i == j)
			{
				vvDist[i][j] = W();//防止溢出最大值+一个不是最大值的距离
				vvpPath[i][j] = i;
			}
		}
	}
    //遍历每个顶点
}

(1)得到顶点个数n

(2)vvDist、vvpPath都是二维数组

(3)根据直接相连的边初始化vvDist、vvpPath，

源点到源点，源点通过一条边直接到达的顶点

复制代码 
//i -> k k -> j 与 i -> j
//中间顶点k
for (int k = 0; k < n; ++k)
{
	//每对顶点i、j
	for (int i = 0; i < n; ++i)
	{
		for (int j = 0; j < n; ++j)
		{
			if (vvDist[i][k] != W_MAX && vvDist[k][j] != W_MAX
				&& vvDist[i][k] + vvDist[k][j] < vvDist[i][j])
			{
				vvDist[i][j] = vvDist[i][k] + vvDist[k][j];
				vvpPath[i][j] = vvpPath[k][j];
			}
		}
	}	
}

(1)通过三重循环（k, i, j），逐步考虑中间顶点k(外层循环)，

更新所有顶点对(i,j)（内层循环）的距离

(2)vvpPath[i][j]的父亲节点是vvpPath[k][j]，这是因为 i -> k k -> j 中过程中 k 与 j 不一定是直接相连vvpPath[k][j]存放的就是 k到j 路径中的倒数第二个顶点的下标

复制代码 
			for (int i = 0; i < n; ++i)
			{
				if (vvDist[i][i] < 0)
					return false;
			}

如果图中存在负权环，那么经过三重循环后，某点到自己的权值和小于0

据此判断负权环

完整呈现

复制代码 
		bool FloydWarShall(vector<vector<W>>& vvDist, vector<vector<int>>& vvpPath)
		{
			int n = _vertexes.size();
			vvDist.resize(n, vector<W>(n, W_MAX));
			vvpPath.resize(n, vector<int>(n, -1));
			//初始化通过一条边直接相连接的顶点
			for (int i = 0; i < n; ++i)
			{
				for (int j = 0; j < n; ++j)
				{
					if (_matrix[i][j] != W_MAX)
					{
						vvDist[i][j] = _matrix[i][j];
						vvpPath[i][j] = i;
					}

					if (i == j)
					{
						vvDist[i][j] = W();//防止溢出最大值+一个不是最大值的距离
						vvpPath[i][j] = i;
					}
				}
			}
			//i -> k k -> j 与 i -> j
			//中间顶点k
			for (int k = 0; k < n; ++k)
			{
				//每对顶点i、j
				for (int i = 0; i < n; ++i)
				{
					for (int j = 0; j < n; ++j)
					{
						if (vvDist[i][k] != W_MAX && vvDist[k][j] != W_MAX
							&& vvDist[i][k] + vvDist[k][j] < vvDist[i][j])
						{
							vvDist[i][j] = vvDist[i][k] + vvDist[k][j];
							vvpPath[i][j] = vvpPath[k][j];
						}
					}
				}	
			}

			for (int i = 0; i < n; ++i)
			{
				if (vvDist[i][i] < 0)
					return false;
			}

			return true;
		}

2.总结

算法 时间复杂度 空间复杂度 适用场景
Dijkstra O(V²) → O((V+E)logV) O(V²) 非负权图，稀疏图优先堆优化
Bellman O(V³) → O(VE) O(V²) 含负权边单源问题，邻接表优化
Floyd O(V³) O(V²) 多源最短路径，小规模图
相关推荐
小小小CTFER几秒前
理论题] 2025 年 “技耀泉城” 海右技能人才大赛网络安全知识竞赛题目（二）
算法·安全·web安全
断剑zou天涯2 小时前
【算法笔记】暴力递归尝试
java·笔记·算法
油泼辣子多加2 小时前
【实战】自然语言处理--长文本分类（1）DPCNN算法
算法·自然语言处理·分类
I＇m a winner3 小时前
基于YOLO算法的医疗应用专题：第一章 计算机视觉与深度学习概述
算法·yolo·计算机视觉
vir023 小时前
P1928 外星密码（dfs）
java·数据结构·算法·深度优先·1024程序员节
喜欢吃燃面4 小时前
数据结构算法题：list
开发语言·c++·学习·算法·1024程序员节
胡萝卜3.04 小时前
C++ list核心接口与实战技巧
数据结构·c++·list·list使用
寂静山林4 小时前
UVa 12991 Game Rooms
算法·1024程序员节
仟千意4 小时前
数据结构：排序篇
数据结构
热门推荐
01BongoCat - 跨平台键盘猫动画工具02GitHub 镜像站点03UV安装并设置国内源04Linux下V2Ray安装配置指南05jdk21下载、安装（Windows、Linux、macOS）06GitLab 零基础入门指南：从安装到项目管理全流程07NVIDIA显卡驱动、CUDA、cuDNN 和 TensorRT 版本匹配指南08KGG转MP3工具|非KGM文件|解密音频09Labelme从安装到标注：零基础完整指南10在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）