这些概念和模型都是很基础的内容，但是问题就出在这个基础两个字上面，现在出现了N个版本，导致很多人在这里知识点遗漏，所以非常需要梳理一次！
一、3D到2D-世界如何呈现于我们的图像之中
世界坐标系 (World)
↓ 外参（R, t）
相机坐标系 (Camera)
↓ 透视投影（除以 Z）
归一化像平面 (Normalized Image Plane)
↓ 内参（fx, fy, cx, cy）
像素坐标系 (Image / Pixel)1.1世界坐标 → 相机坐标（外参）
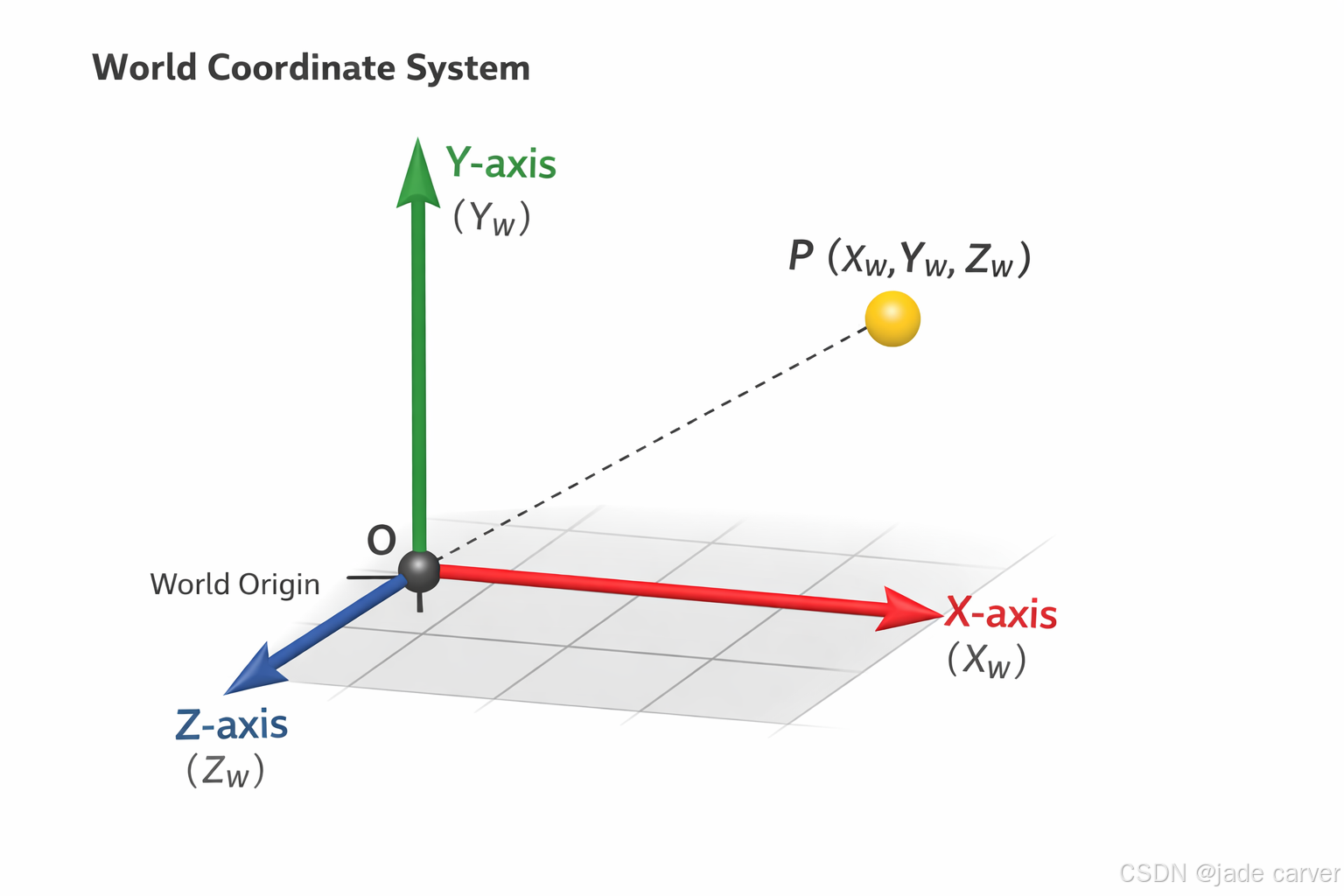
世界坐标系（World Coordinate）
世界坐标系是三维空间中描述物体绝对位置的基准坐标系，广泛应用于计算机图形学、机器人学及计算机视觉等领域。在计算机视觉中，世界坐标系作为环境参考基准，与摄像机坐标系通过旋转矩阵和平移向量转换，实现三维空间点到二维图像平面的映射
所有 3D 点定义在一个统一坐标系中，比如 3DGS 的高斯中心 (X_w, Y_w, Z_w)
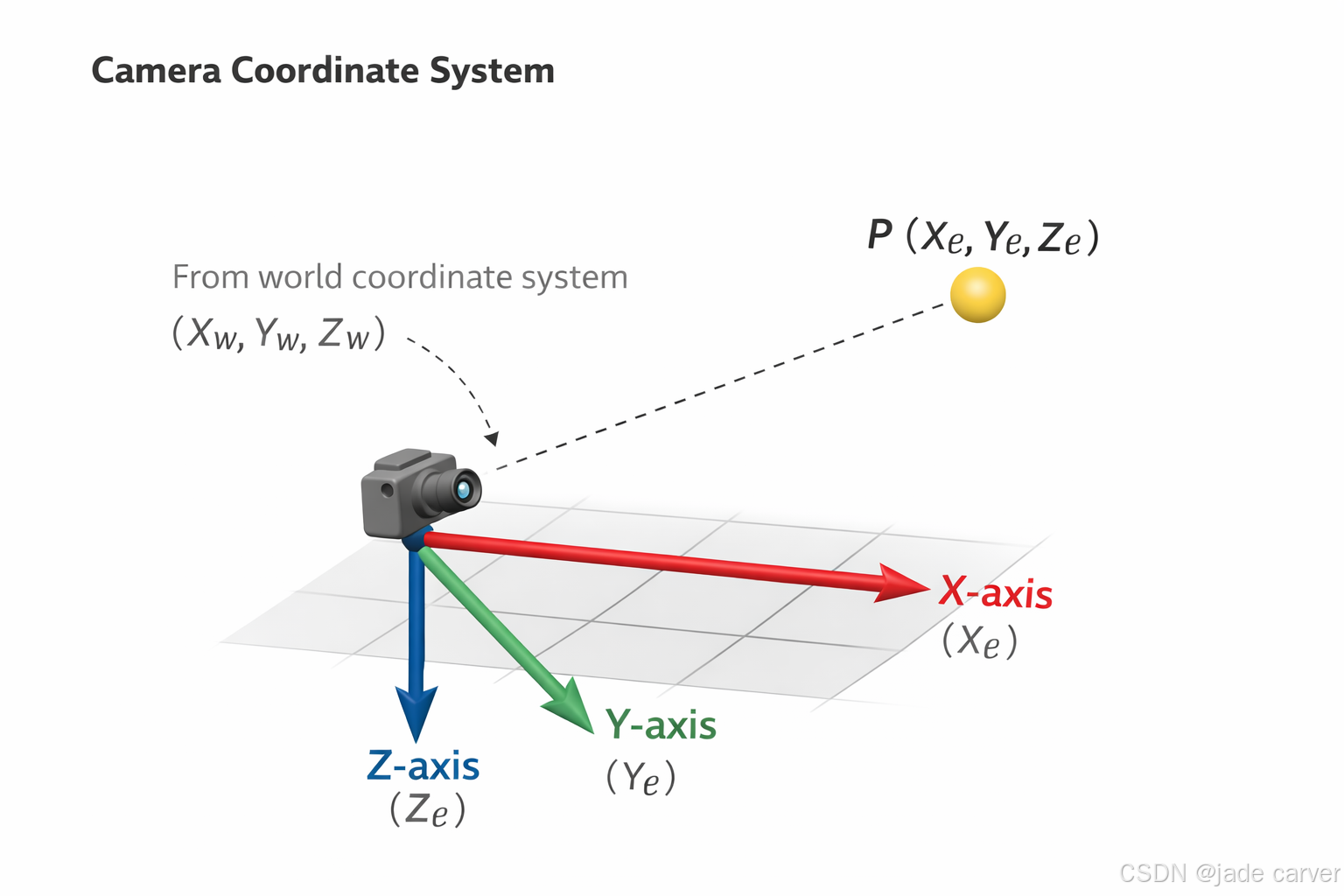
相机坐标系（Camera Coordinate）
相机坐标系是以相机光心（聚焦中心）为原点建立的三维直角坐标系。该坐标系通过刚体变换（旋转矩阵和平移向量）实现与世界坐标系的转换。
原点在 **相机光心，**通常定义：
- X：向右
- Y：向下
- Z：向前（指向拍摄方向）
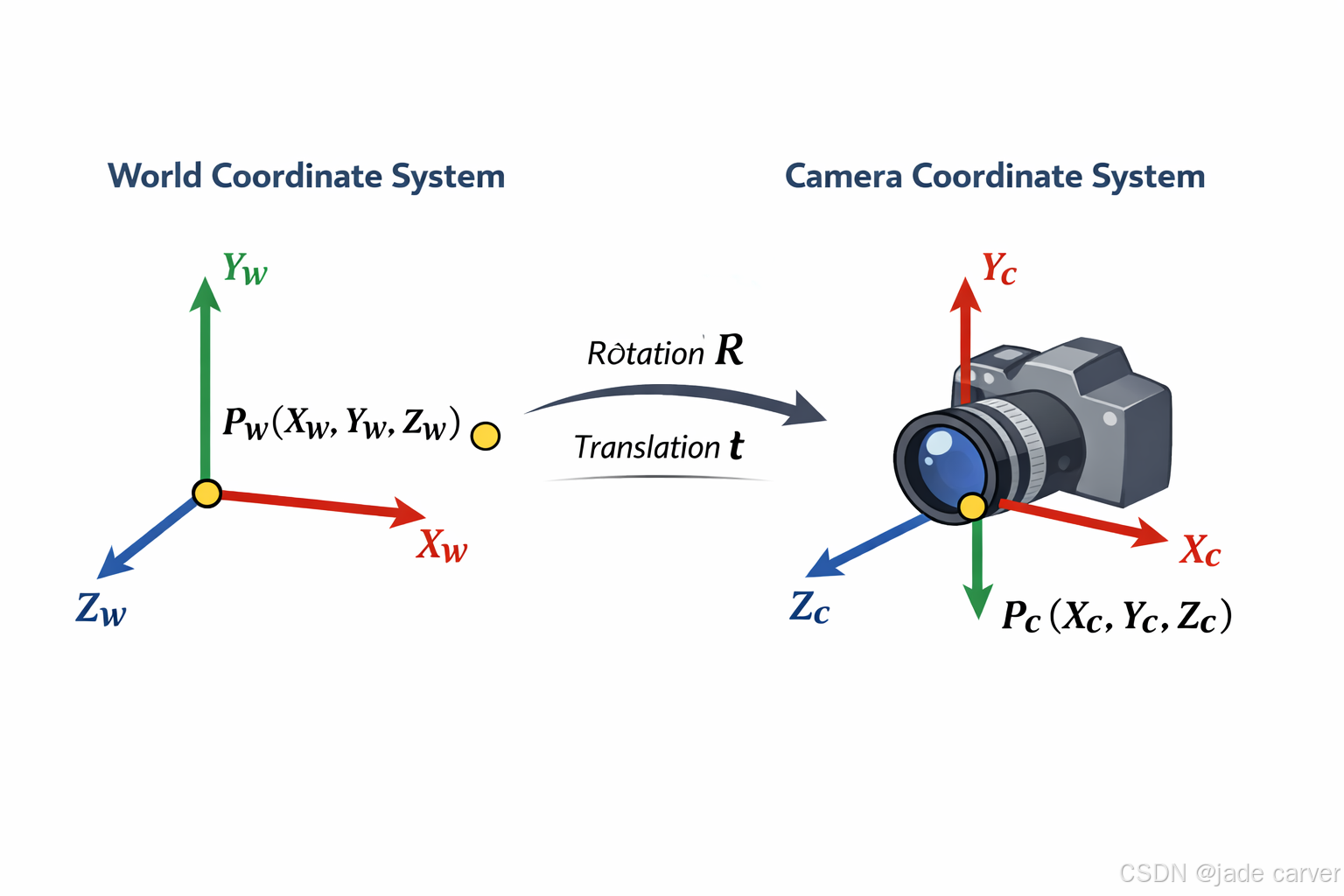
外参：旋转 + 平移
相机在世界中有一个姿态：
- 旋转矩阵
R（3×3） - 平移向量
t（3×1）
世界点 → 相机点通过这样转换：
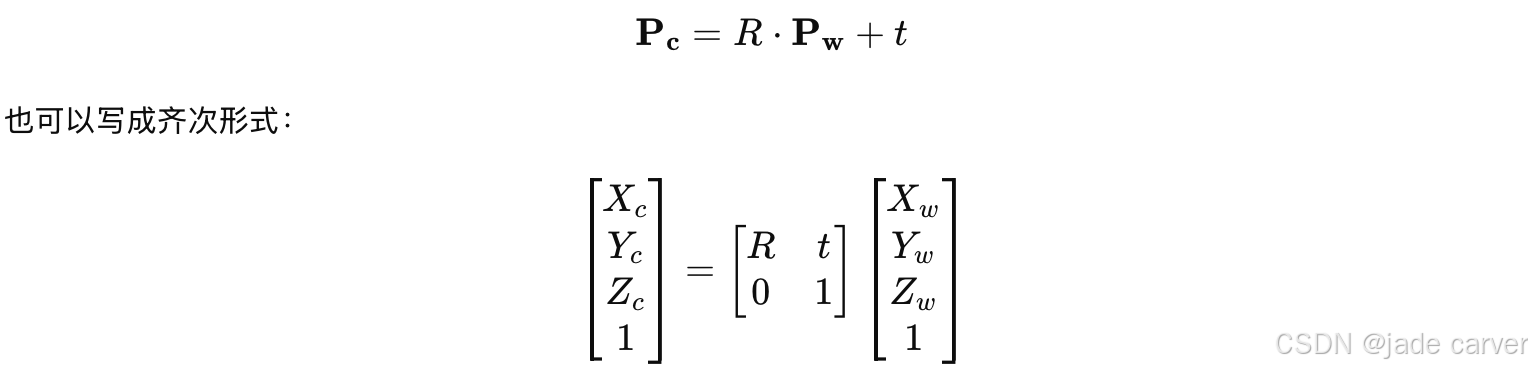
1.2.相机坐标（X，Y，Z） → 成像平面坐标系（x,y）-以pinhole为例
以O点为中心，可以构建一个下图中的相似三角形(注意图中O'P'的距离虽然不是X'，想象把P'分别投影到x', y'的三角形依然是相似的：
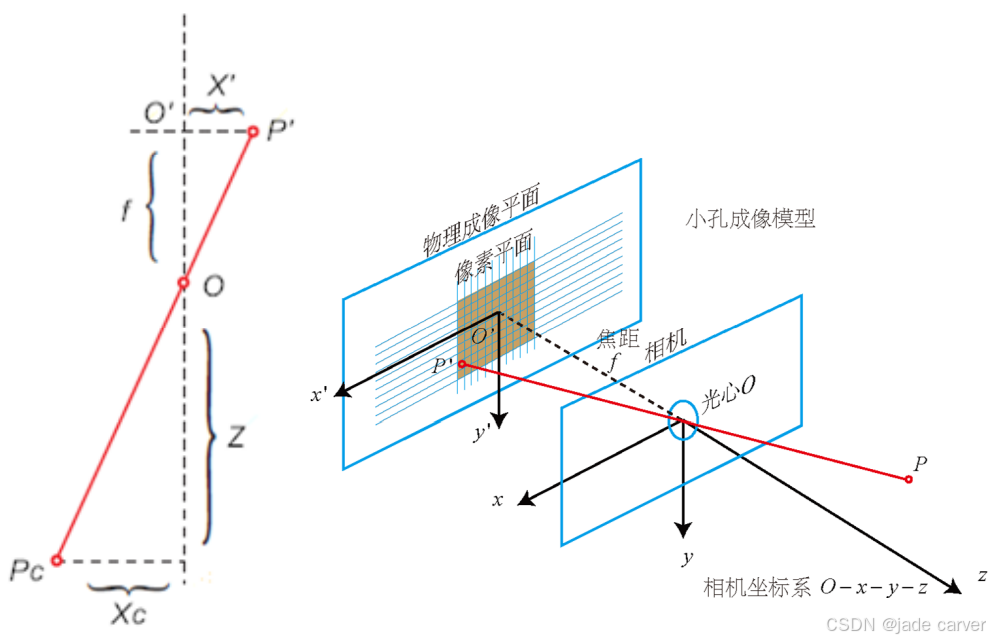
根据相似三角形，可以构建如下关系：
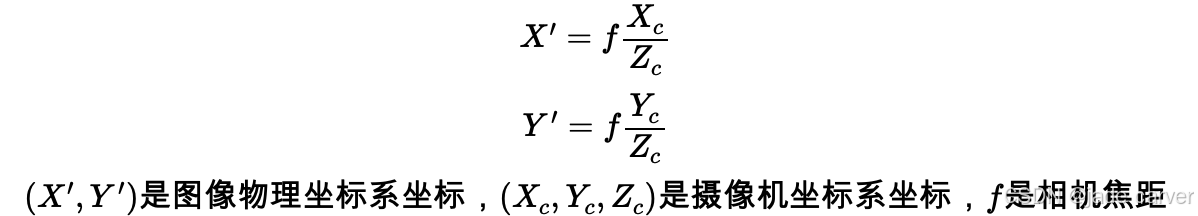
用矩阵表示如下：
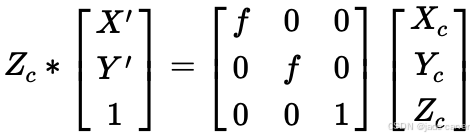
这里的
是深度，具体来说，就是在相机坐标系下的绝对深度，深度很重要，后面还会专门提到逆深度，因为逆深度可以完美表达我们人眼中近大远小的现象。
1.3归一化图像坐标（Normalized Plane）
归一化图像坐标的定义
在标准 pinhole 模型中，成像平面在距离相机原点 O 的位置为 f（焦距），投影公式为：
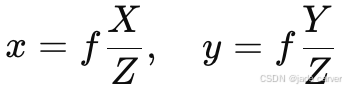
如果我们把焦距标准化为 f=1，就得到 归一化图像坐标：
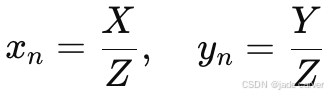
- 单位 不是像素，而是相机坐标系下的比值（长度比）。
- 原点在 光轴中心（即相机光心正下方）。
- 这是一个虚拟成像平面，通常称为 Normalized Plane。
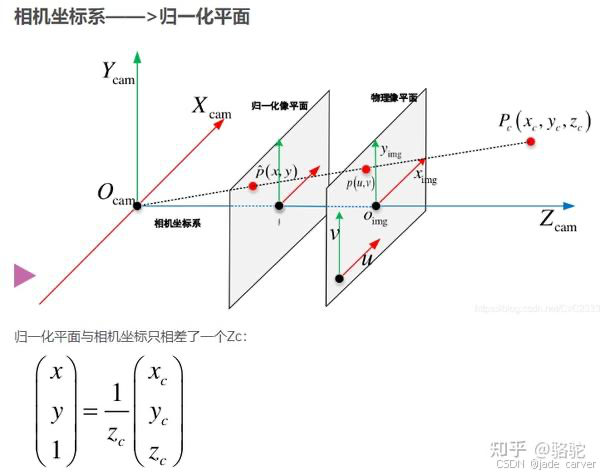
物理意义
- 投影到归一化平面，去掉了焦距的影响，保留了 透视缩放 的本质。
- 点离相机越远（Z 大），归一化坐标越小；点离相机越近（Z 小），归一化坐标越大。
- 这个坐标系常用于 计算视差、相机内参归一化 ，或者用于深度估计网络中，注意，这里已经是用逆深度
了
1.4归一化坐标+相机内参 → 像素坐标
| 特性 | 图像物理坐标系 | 图像像素坐标系 |
|---|---|---|
| 单位 | 长度单位（米、毫米等） | 像素 |
| 原点 | 光轴中心（图像中心） | 左上角 |
| 方向 | X 向右，Y 向上（通常） | u 向右，v 向下 |
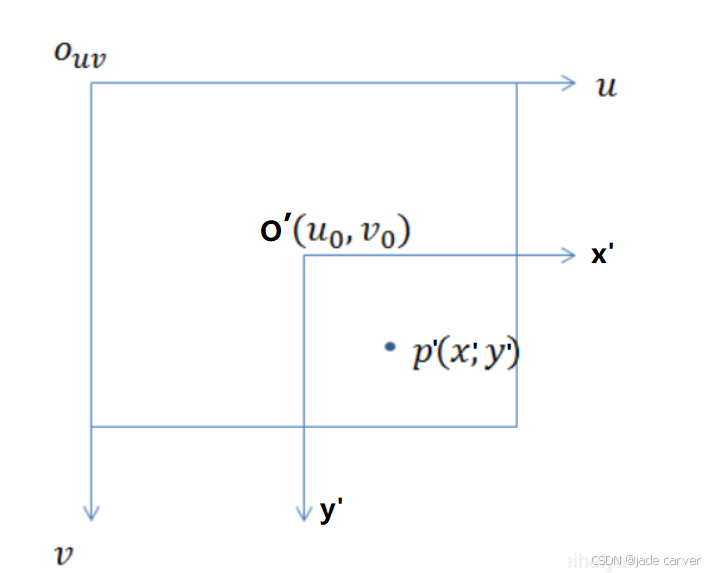
图像物理坐标系采用的是长度单位，坐标原点一般是图片中心位置；而图像像素坐标系采用的是像素单位，坐标原点一般是图片左上角位置，如下图所示，因此图像物理坐标系转换成图像像素坐标系需要两步：
- 根据一个像素占多少长度，将长度单位转换为像素单位
- 将转换后的像素坐标进行平移，使坐标原点为左上角
相机内参矩阵 K
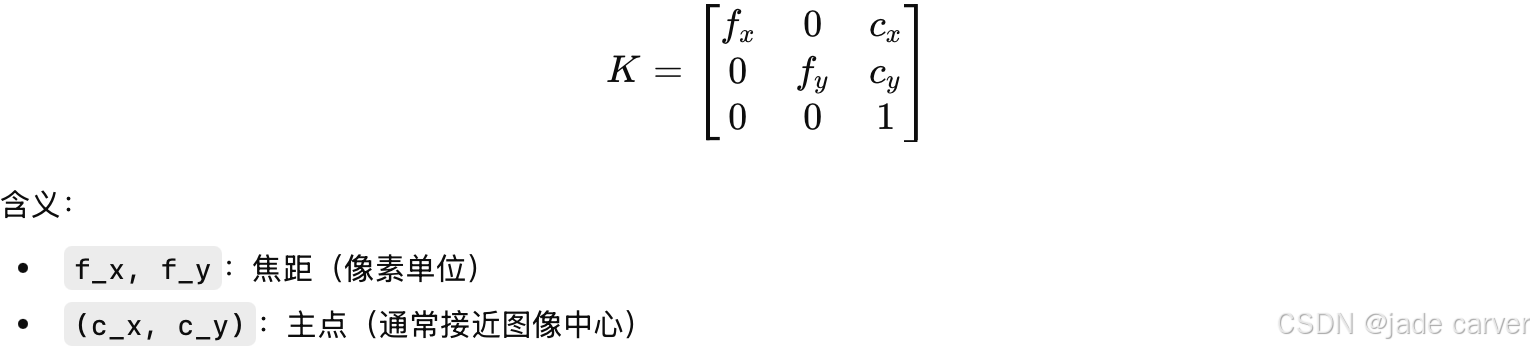
从归一化坐标到像素坐标
详细过程
第一步：长度单位 → 像素单位
- 根据像素尺寸或者焦距，长度单位变为像素单位。
- 对应公式就是：
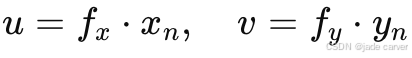
这里 fx,fy 就表示 每个方向像素长度对应多少物理长度。
第二步：坐标平移（原点从中心移到左上角）
平移主点到左上角，公式为：
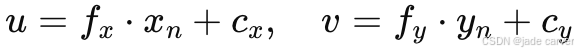
- cx,cy 是图像中心到左上角的偏移。
- 这一步对应 相机内参矩阵 K 中的偏移量。
总结
二、深度与逆深度
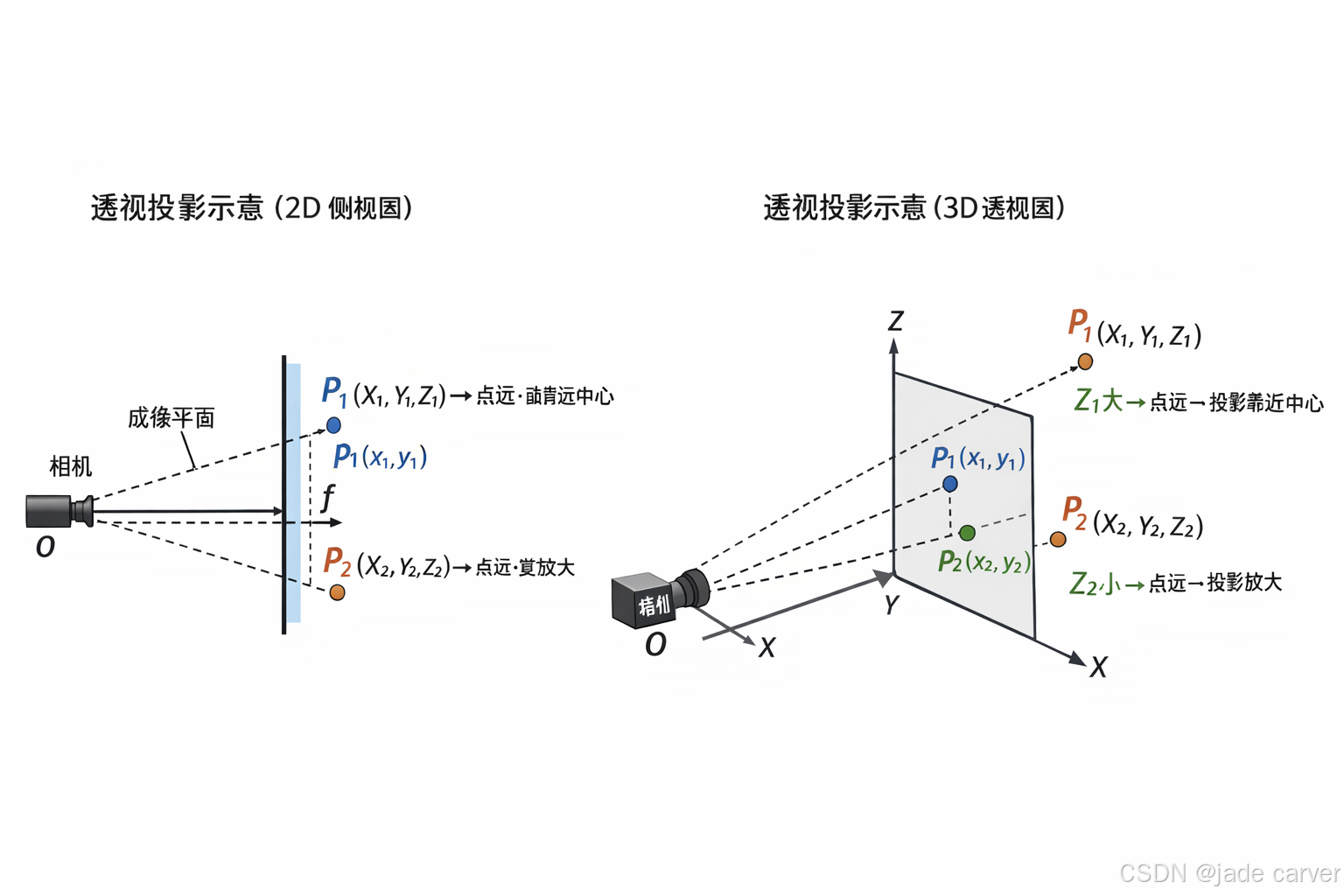
2.1深度（Depth, Z）
定义
数学关系
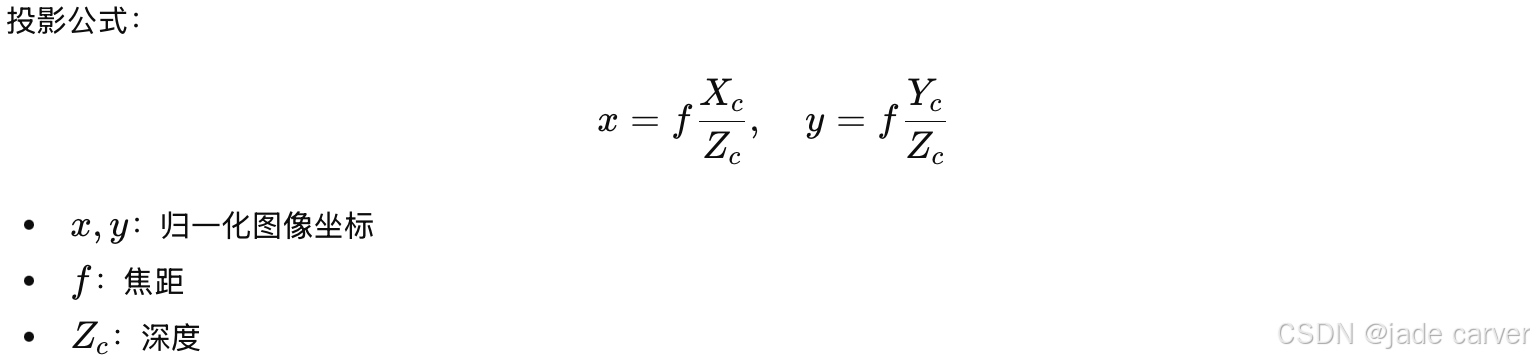
深度越大，投影越靠近图像中心（透视收缩效果）
| 深度 Z | 投影效果 |
|---|---|
| 小（近） | 放大、明显位移 |
| 大（远） | 缩小、收紧到中心 |
2.2逆深度（Inverse Depth, 1/Z）
定义
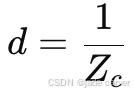
为什么用逆深度？
| Z_c | 1/Z_c |
|---|---|
| 1m | 1.0 |
| 2m | 0.5 |
| 10m | 0.1 |
| 100m | 0.01 |
2.3从 SfM 点到图像深度示例
假设：
三、在3DGS中深度与SfM的结合
3.1问题背景
深度估计模型输出： 通常是单目图像的相对深度，没有绝对尺度，单位和 SfM 点云世界坐标不一致，远处/近处比例对，但整体大小、偏移是未知的
**SfM 结果：**提供稀疏点云（世界坐标系），可以算出相机位姿和稀疏深度（稀疏但尺度真实）可以作为单目深度尺度参考
目标： 利用单目深度模型的密集深度 → 转换成相机坐标系的逆深度，但必须 匹配 SfM 的尺度和偏移，否则渲染 / 优化不收敛。
3.2scale & offset 对齐
使用线性变换对齐
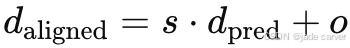
- s：尺度因子（scale）
- o：偏移量（offset）
- 目标：让大模型估计的逆深度 整体匹配 SfM 的稀疏深度尺度
求解 scale & offset
总结
- 大模型深度是相对尺度 ， 不能直接用
- SfM 提供绝对尺度参考 ，可以纠正整体缩放和偏移
- 对齐后：
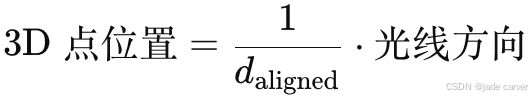
- 在3DGS后续的深度loss中，由于统一到了SfM坐标系，故可以以此作为ground truth来优化
| 数据源 | 特性 | 使用方式 |
|---|---|---|
| 大模型逆深度 (d_\text{pred}) | 相对尺度，密集 | 提供高密度几何 / 细节 |
| SfM 绝对尺度点云 | 稀疏，绝对尺度 | 用于 scale & offset 对齐 |
| 对齐后的逆深度 (d_\text{aligned}) | 密集 + 绝对尺度 | 初始化高斯点，投影渲染 |