排序算法（golang实现）

https://www.runoob.com/w3cnote/ten-sorting-algorithm.html

复杂度

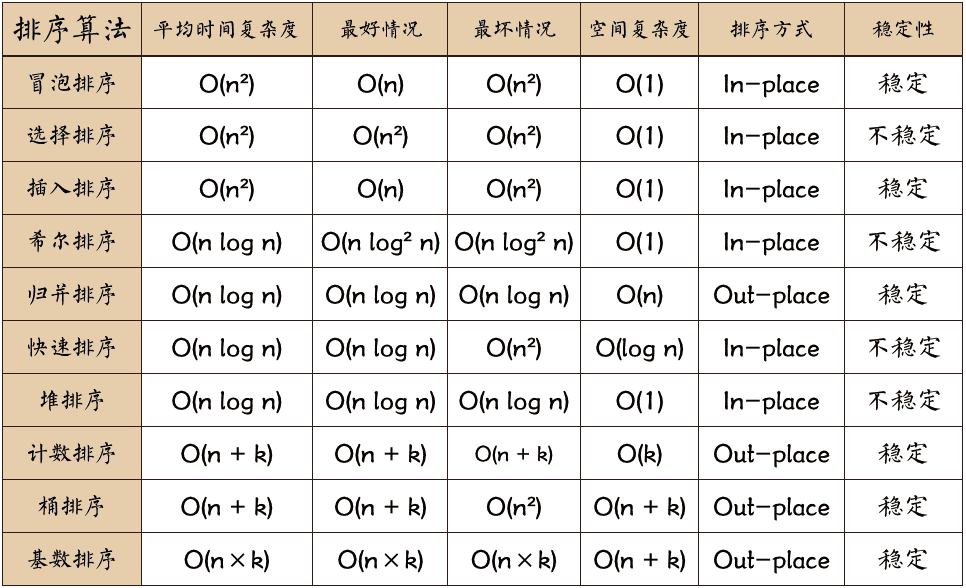
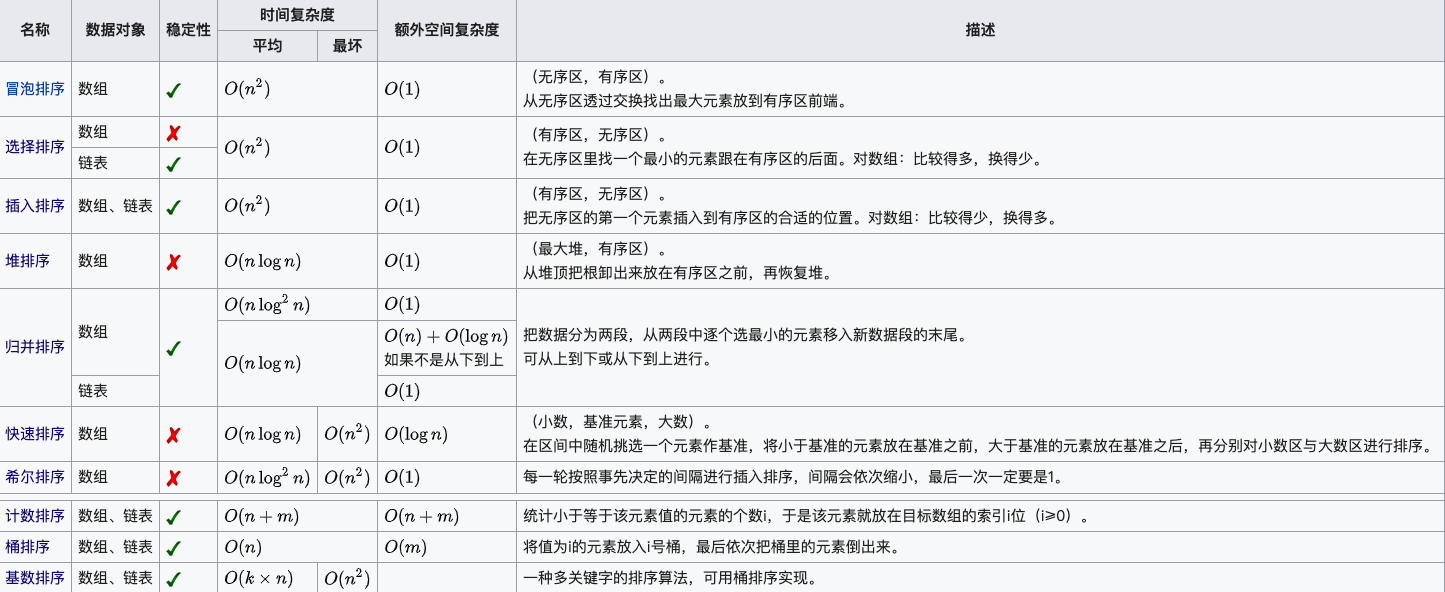
冒泡排序

算法步骤

1. 比较相邻元素：从列表的第一个元素开始，比较相邻的两个元素。
2. 交换位置：如果前一个元素比后一个元素大，则交换它们的位置。
3. 重复遍历：对列表中的每一对相邻元素重复上述步骤，直到列表的末尾。这样，最大的元素会被"冒泡"到列表的最后。
4. 缩小范围：忽略已经排序好的最后一个元素，重复上述步骤，直到整个列表排序完成。

时间复杂度

• 最坏情况：O(n²)，当列表是逆序时。
• 最好情况：O(n)，当列表已经有序时。
• 平均情况：O(n²)。

空间复杂度

• O(1)，因为冒泡排序是原地排序算法，不需要额外的存储空间。

优缺点

• 优点：

  • 实现简单，代码易于理解。
  • 原地排序，不需要额外的存储空间。

• 缺点：

  • 效率较低，尤其是对于大规模数据集。
  • 不适合处理几乎已经有序的列表，因为仍然需要进行多次遍历。

代码实现

func bubbleSort(arr []int) []int {
	length := len(arr)
	for i := 0; i < length; i++ {
		for j := 0; j < length-1-i; j++ {
			if arr[j] > arr[j+1] {
				arr[j], arr[j+1] = arr[j+1], arr[j]
			}
		}
	}
	return arr
}

选择排序

算法步骤

1. 初始化：将列表分为已排序部分和未排序部分。初始时，已排序部分为空，未排序部分为整个列表。
2. 查找最小值：在未排序部分中查找最小的元素。
3. 交换位置：将找到的最小元素与未排序部分的第一个元素交换位置。
4. 更新范围：将未排序部分的起始位置向后移动一位，扩大已排序部分的范围。
5. 重复步骤：重复上述步骤，直到未排序部分为空，列表完全有序。

时间复杂度

• 最坏情况：O(n²)，无论输入数据是否有序，都需要进行 n(n-1)/2 次比较。
• 最好情况：O(n²)，即使列表已经有序，仍需进行相同数量的比较。
• 平均情况：O(n²)。

空间复杂度

• O(1)，选择排序是原地排序算法，不需要额外的存储空间。

优缺点

• 优点：

  • 实现简单，代码易于理解。
  • 原地排序，不需要额外的存储空间。
  • 对于小规模数据集，性能尚可接受。

• 缺点：

  • 时间复杂度较高，不适合大规模数据集。
  • 不稳定排序算法（如果存在相同元素，可能会改变它们的相对顺序）。

代码实现

func selectionSort(arr []int) []int {
	length := len(arr)
	for i := 0; i < length-1; i++ {
		min := i
		for j := i + 1; j < length; j++ {
			if arr[min] > arr[j] {
				min = j
			}
		}
		arr[i], arr[min] = arr[min], arr[i]
	}
	return arr
}

插入排序

算法步骤

1. 初始化：将列表分为已排序部分和未排序部分。初始时，已排序部分只包含第一个元素，未排序部分包含剩余元素。
2. 选择元素：从未排序部分中取出第一个元素。
3. 插入到已排序部分：将该元素与已排序部分的元素从后向前依次比较，找到合适的位置插入。
4. 重复步骤：重复上述步骤，直到未排序部分为空，列表完全有序。

时间复杂度

• 最坏情况：O(n²)，当列表是逆序时，每次插入都需要移动所有已排序元素。
• 最好情况：O(n)，当列表已经有序时，只需遍历一次列表。
• 平均情况：O(n²)。

空间复杂度

• O(1)，插入排序是原地排序算法，不需要额外的存储空间。

优缺点

• 优点：

  • 实现简单，代码易于理解。
  • 对小规模数据或基本有序的数据效率较高。
  • 原地排序，不需要额外的存储空间。
  • 稳定排序算法（相同元素的相对顺序不会改变）。

• 缺点：

  • 时间复杂度较高，不适合大规模数据集。

代码实现

func insertionSort(arr []int) []int {
	for i := range arr {
		preIndex := i - 1
		current := arr[i]
		for preIndex >= 0 && arr[preIndex] > current {
			arr[preIndex+1] = arr[preIndex]
			preIndex -= 1
		}
		arr[preIndex+1] = current
	}
	return arr
}

希尔排序

算法步骤

1. 选择增量序列：选择一个增量序列（gap sequence），用于将列表分成若干子列表。常见的增量序列有希尔增量（n/2, n/4, ..., 1）等。
2. 分组插入排序：按照增量序列将列表分成若干子列表，对每个子列表进行插入排序。
3. 缩小增量：逐步缩小增量，重复上述分组和排序过程，直到增量为 1。
4. 最终排序：当增量为 1 时，对整个列表进行一次插入排序，完成排序。

时间复杂度

希尔排序的时间复杂度取决于增量序列的选择：

• 最坏情况：O(n²)，当增量序列选择不当时。
• 最好情况：O(n log n)，当增量序列选择合适时。
• 平均情况：O(n log n) 到 O(n²) 之间。

常见的增量序列：

• 希尔增量：n/2, n/4, ..., 1，时间复杂度为 O(n²)。
• Hibbard 增量：1, 3, 7, 15, ..., 2^k - 1，时间复杂度为 O(n^(3/2))。
• Sedgewick 增量：1, 5, 19, 41, 109, ...，时间复杂度为 O(n^(4/3))。

空间复杂度

• O(1)，希尔排序是原地排序算法，不需要额外的存储空间。

优缺点

• 优点：

  • 相对于简单插入排序，效率更高。
  • 原地排序，不需要额外的存储空间。
  • 适用于中等规模的数据集。

• 缺点 ：

  +时间复杂度依赖于增量序列的选择。

  不稳定排序算法（可能改变相同元素的相对顺序）。

代码实现

func shellSort(arr []int) []int {
	length := len(arr)
	gap := 1
	for gap < length/3 {
		gap = gap*3 + 1
	}
	for gap > 0 {
		for i := gap; i < length; i++ {
			temp := arr[i]
			j := i - gap
			for j >= 0 && arr[j] > temp {
				arr[j+gap] = arr[j]
				j -= gap
			}
			arr[j+gap] = temp
		}
		gap = gap / 3
	}
	return arr
}

归并排序

归并排序的步骤如

1. 分解（Divide）：将待排序的数组分成两个子数组，每个子数组包含大约一半的元素。
2. 解决（Conquer）：递归地对每个子数组进行排序。
3. 合并（Combine）：将两个已排序的子数组合并成一个有序的数组。

通过不断地分解和合并，最终整个数组将被排序。

算法步骤

1. 申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列；
2. 设定两个指针，最初位置分别为两个已经排序序列的起始位置；
3. 比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置；
4. 重复步骤 3 直到某一指针达到序列尾；
5. 将另一序列剩下的所有元素直接复制到合并序列尾。

时间复杂度

• 分解：每次将列表分成两半，需要 O(log n) 层递归。
• 合并：每层递归需要 O(n) 的时间来合并子列表。
• 总时间复杂度：O(n log n)。

空间复杂度

• O(n)，归并排序需要额外的空间来存储临时列表。

优缺点

• 优点：

  • 时间复杂度稳定为 O(n log n)，适合大规模数据。
  • 稳定排序算法（相同元素的相对顺序不会改变）。
  • 适合外部排序（如对磁盘文件进行排序）。

• 缺点：

  • 需要额外的存储空间，空间复杂度为 O(n)。
  • 对于小规模数据，性能可能不如插入排序等简单算法。

代码实现

func mergeSort(arr []int) []int {
        length := len(arr)
        if length < 2 {
                return arr
        }
        middle := length / 2
        left := arr[0:middle]
        right := arr[middle:]
        return merge(mergeSort(left), mergeSort(right))
}

func merge(left []int, right []int) []int {
        var result []int
        for len(left) != 0 && len(right) != 0 {
                if left[0] <= right[0] {
                        result = append(result, left[0])
                        left = left[1:]
                } else {
                        result = append(result, right[0])
                        right = right[1:]
                }
        }

        for len(left) != 0 {
                result = append(result, left[0])
                left = left[1:]
        }

        for len(right) != 0 {
                result = append(result, right[0])
                right = right[1:]
        }

        return result
}

快速排序

算法步骤

1. 选择基准元素：从列表中选择一个元素作为基准（pivot）。选择方式可以是第一个元素、最后一个元素、中间元素或随机元素。
2. 分区：将列表重新排列，使得所有小于基准元素的元素都在基准的左侧，所有大于基准元素的元素都在基准的右侧。基准元素的位置在分区完成后确定。
3. 递归排序：对基准元素左侧和右侧的子列表分别递归地进行快速排序。
4. 合并：由于分区操作是原地进行的，递归结束后整个列表已经有序。

时间复杂度

• 分解：每次将列表分成两半，需要 O(log n) 层递归。
• 合并：每层递归需要 O(n) 的时间来合并子列表。
• 总时间复杂度：O(n log n)。

空间复杂度

• O(n)，归并排序需要额外的空间来存储临时列表。

优缺点

• 优点：

  • 时间复杂度稳定为 O(n log n)，适合大规模数据。
  • 稳定排序算法（相同元素的相对顺序不会改变）。
  • 适合外部排序（如对磁盘文件进行排序）。

• 优点：

  • 需要额外的存储空间，空间复杂度为 O(n)。
  • 对于小规模数据，性能可能不如插入排序等简单算法。

代码实现

// quickSort 是快速排序的入口函数，接收一个整数切片并返回排序后的切片
func quickSort(arr []int) []int {
    // 调用内部的递归排序函数，初始排序范围为整个数组
    // 从索引0到最后一个元素的索引len(arr)-1
    return _quickSort(arr, 0, len(arr)-1)
}

// _quickSort 是内部使用的递归排序函数
// 参数:
//   arr: 要排序的数组
//   left: 当前排序区间的左边界索引
//   right: 当前排序区间的右边界索引
func _quickSort(arr []int, left, right int) []int {
    // 递归终止条件：当左边界大于等于右边界时，说明子数组已排序或为空
    if left < right {
        // 对当前区间进行分区操作，返回基准值的最终位置
        partitionIndex := partition(arr, left, right)
        
        // 递归排序基准值左侧的子数组（不包含基准值本身）
        _quickSort(arr, left, partitionIndex-1)
        // 递归排序基准值右侧的子数组（不包含基准值本身）
        _quickSort(arr, partitionIndex+1, right)
    }
    // 返回排序后的数组
    return arr
}

// partition 分区函数，将数组分区并返回基准值的最终位置
// 分区规则：所有小于基准值的元素放左边，大于等于基准值的元素放右边
// 参数:
//   arr: 要分区的数组
//   left: 分区区间的左边界
//   right: 分区区间的右边界
// 返回值: 基准值的最终索引位置
func partition(arr []int, left, right int) int {
    // 选择最左边的元素作为基准值(pivot)
    pivot := left
    // index 标记小于基准值区域的右边界（初始为基准值右侧第一个元素）
    index := pivot + 1

    // 遍历从index到right的所有元素
    for i := index; i <= right; i++ {
        // 如果当前元素小于基准值，将其交换到小于基准值的区域
        if arr[i] < arr[pivot] {
            swap(arr, i, index)
            // 扩大小于基准值的区域
            index += 1
        }
    }
    // 将基准值交换到正确位置（小于基准值区域的最后一个位置）
    swap(arr, pivot, index-1)
    // 返回基准值的最终索引
    return index - 1
}

// swap 辅助函数，用于交换数组中两个指定索引位置的元素
// 参数:
//   arr: 要操作的数组
//   i: 第一个元素的索引
//   j: 第二个元素的索引
func swap(arr []int, i, j int) {
    // 利用Go语言的多重赋值特性交换元素
    arr[i], arr[j] = arr[j], arr[i]
}

堆排序

算法步骤

1. 创建一个堆 H[0......n-1]；
2. 把堆首（最大值）和堆尾互换；
3. 把堆的尺寸缩小 1，并调用 shift_down(0)，目的是把新的数组顶端数据调整到相应位置；
4. 重复步骤 2，直到堆的尺寸为 1。

时间复杂度

• 构建最大堆：O(n)。
• 每次调整堆：O(log n)，总共需要调整 n-1 次。
• 总时间复杂度：O(n log n)。

空间复杂度

• O(1)，堆排序是原地排序算法，不需要额外的存储空间。

优缺点

• 优点：

  • 时间复杂度稳定为 O(n log n)，适合大规模数据。
  • 原地排序，不需要额外的存储空间。

• 缺点：

  • 不稳定排序算法（可能改变相同元素的相对顺序）。
  • 对于小规模数据，性能可能不如插入排序等简单算法。

代码实现

// heapSort 是堆排序的入口函数，接收一个整数切片并返回排序后的切片
func heapSort(arr []int) []int {
    // 获取数组长度
    arrLen := len(arr)
    
    // 第一步：将无序数组构建成最大堆
    buildMaxHeap(arr, arrLen)
    
    // 第二步：逐步提取最大值并调整堆，完成排序
    // 从最后一个元素开始，逐步将堆顶的最大值交换到数组末尾
    for i := arrLen - 1; i >= 0; i-- {
        // 将堆顶元素（当前最大值）与当前未排序部分的最后一个元素交换
        swap(arr, 0, i)
        
        // 缩小堆的范围（已排序的元素不再参与堆调整）
        arrLen -= 1
        
        // 从堆顶开始重新调整堆结构，维持最大堆性质
        heapify(arr, 0, arrLen)
    }
    
    return arr
}

// buildMaxHeap 将数组构建成最大堆
// 参数:
//   arr: 要处理的数组
//   arrLen: 数组的长度
func buildMaxHeap(arr []int, arrLen int) {
    // 从最后一个非叶子节点开始向前遍历，依次对每个节点执行堆化操作
    // 最后一个非叶子节点的索引为 arrLen/2（完全二叉树性质）
    for i := arrLen / 2; i >= 0; i-- {
        heapify(arr, i, arrLen)
    }
}

// heapify 堆化操作，确保以 i 为根的子树满足最大堆性质
// 最大堆性质：父节点的值大于等于其左右子节点的值
// 参数:
//   arr: 要处理的数组
//   i: 当前需要堆化的节点索引
//   arrLen: 当前堆的有效长度（未排序部分的长度）
func heapify(arr []int, i, arrLen int) {
    // 计算左子节点的索引（2*i + 1）
    left := 2*i + 1
    // 计算右子节点的索引（2*i + 2）
    right := 2*i + 2
    
    // 假设当前节点是最大值节点
    largest := i
    
    // 如果左子节点存在（索引小于堆长度）且左子节点值大于当前最大值
    if left < arrLen && arr[left] > arr[largest] {
        // 更新最大值节点为左子节点
        largest = left
    }
    
    // 如果右子节点存在且右子节点值大于当前最大值
    if right < arrLen && arr[right] > arr[largest] {
        // 更新最大值节点为右子节点
        largest = right
    }
    
    // 如果最大值节点不是当前节点（需要调整）
    if largest != i {
        // 交换当前节点与最大值节点
        swap(arr, i, largest)
        
        // 递归对受影响的子节点进行堆化（因为交换后子树可能不再满足堆性质）
        heapify(arr, largest, arrLen)
    }
}

// swap 辅助函数，用于交换数组中两个指定索引位置的元素
// 参数:
//   arr: 要操作的数组
//   i: 第一个元素的索引
//   j: 第二个元素的索引
func swap(arr []int, i, j int) {
    arr[i], arr[j] = arr[j], arr[i]
}

桶排序

算法步骤

1. 初始化桶：根据数据的范围和分布，创建若干个桶。
2. 分配元素：遍历待排序的列表，将每个元素分配到对应的桶中。
3. 排序每个桶：对每个桶中的元素进行排序（可以使用插入排序、快速排序等）。
4. 合并桶：将所有桶中的元素按顺序合并，得到最终排序结果。

时间复杂度

• 分配元素：O(n)，遍历列表一次。
• 排序每个桶：假设每个桶中的元素数量为 m，则排序一个桶的时间复杂度为 O(m log m)。如果桶的数量为 k，则总时间复杂度为 O(k * m log m)。
• 合并桶：O(n)，遍历所有桶一次。
• 总时间复杂度：O(n + k * m log m)，其中 n 是列表长度，k 是桶的数量，m 是每个桶的平均元素数量。

空间复杂度

• O(n + k)，需要额外的存储空间来存放桶和排序后的结果。

优缺点

• 优点：

  • 当数据分布均匀时，性能优异。
  • 适合外部排序（如对磁盘文件进行排序）。

• 缺点：

  • 当数据分布不均匀时，某些桶中的元素数量过多，导致性能下降。
  • 需要额外的存储空间。

代码实现

// bucketSort 实现桶排序算法
// 参数：
//   arr: 待排序的浮点数切片
//   bucketCount: 桶的数量
// 返回值：
//   排序后的浮点数切片
func bucketSort(arr []float64, bucketCount int) []float64 {
	if len(arr) == 0 {
		return arr
	}

	// 1. 找到数组中的最大值和最小值，确定数据范围
	minVal, maxVal := arr[0], arr[0]
	for _, val := range arr {
		if val < minVal {
			minVal = val
		}
		if val > maxVal {
			maxVal = val
		}
	}

	// 计算每个桶的数值范围
	rangeVal := (maxVal - minVal) / float64(bucketCount)

	// 2. 初始化桶
	buckets := make([][]float64, bucketCount)
	for i := range buckets {
		buckets[i] = make([]float64, 0)
	}

	// 3. 将元素分配到对应的桶中
	for _, val := range arr {
		// 计算元素应该放入哪个桶
		index := int((val - minVal) / rangeVal)
		// 处理边界情况（最大值可能会超出最后一个桶的范围）
		if index == bucketCount {
			index = bucketCount - 1
		}
		buckets[index] = append(buckets[index], val)
	}

	// 4. 对每个桶进行排序，并合并并合并结果
	result := make([]float64, 0, len(arr))
	for _, bucket := range buckets {
		if len(bucket) > 0 {
			// 对当前桶使用内置排序
			sort.Float64s(bucket)
			// 将排序后的桶元素合并到结果中
			result = append(result, bucket...)
		}
	}

	return result
}

计数排序

算法步骤

1. 统计频率：遍历待排序的列表，统计每个元素出现的次数，存储在一个计数数组中。
2. 累加频率：将计数数组中的值累加，得到每个元素在排序后列表中的最后一个位置。
3. 构建有序列表：遍历待排序的列表，根据计数数组中的位置信息，将元素放到正确的位置。
4. 输出结果：将排序后的列表输出。

代码实现

func countingSort(arr []int, maxValue int) []int {
        bucketLen := maxValue + 1
        bucket := make([]int, bucketLen) // 初始为0的数组

        sortedIndex := 0
        length := len(arr)

        for i := 0; i < length; i++ {
                bucket[arr[i]] += 1
        }

        for j := 0; j < bucketLen; j++ {
                for bucket[j] > 0 {
                        arr[sortedIndex] = j
                        sortedIndex += 1
                        bucket[j] -= 1
                }
        }

        return arr
}

基数排序

算法步骤

1. 确定最大位数：找到列表中最大数字的位数，确定需要排序的轮数。
2. 按位排序：从最低位开始，依次对每一位进行排序（通常使用计数排序或桶排序作为子排序算法）。
3. 合并结果：每一轮排序后，更新列表的顺序，直到所有位数排序完成。

基数排序 vs 计数排序 vs 桶排序

基数排序有两种方法：

这三种排序算法都利用了桶的概念，但对桶的使用方法上有明显差异：

• 基数排序：根据键值的每位数字来分配桶；
• 计数排序：每个桶只存储单一键值；
• 桶排序：每个桶存储一定范围的数值；

代码实现

// 获取数字的第d位数字（从0开始，0表示个位）
func getDigit(num, d int) int {
	// 计算10^d
	pow := 1
	for i := 0; i < d; i++ {
		pow *= 10
	}
	// 取第d位数字
	return (num / pow) % 10
}

// 基数排序实现
func radixSort(arr []int) []int {
	if len(arr) <= 1 {
		return arr
	}

	// 1. 找到最大值，确定最大位数
	maxVal := arr[0]
	for _, num := range arr {
		if num > maxVal {
			maxVal = num
		}
	}

	// 计算最大位数
	maxDigits := 0
	temp := maxVal
	for temp > 0 {
		temp /= 10
		maxDigits++
	}

	// 2. 按每位进行排序
	result := make([]int, len(arr))
	copy(result, arr)

	for d := 0; d < maxDigits; d++ {
		// 使用计数排序对第d位进行排序
		count := make([]int, 10) // 0-9共10个数字

		// 计数每个数字出现的次数
		for _, num := range result {
			digit := getDigit(num, d)
			count[digit]++
		}

		// 计算前缀和，确定每个数字在结果中的位置
		for i := 1; i < 10; i++ {
			count[i] += count[i-1]
		}

		// 从后往前遍历，保持排序稳定性
		temp := make([]int, len(result))
		for i := len(result) - 1; i >= 0; i-- {
			digit := getDigit(result[i], d)
			count[digit]--
			temp[count[digit]] = result[i]
		}

		result = temp
	}

	return result
}