文章目录
- [1. 节点与树的基本定义](#1. 节点与树的基本定义)
- [2. 手搓一个二叉树](#2. 手搓一个二叉树)
- [3. 二叉树的前中后序遍历](#3. 二叉树的前中后序遍历)
-
- [3.1. 递归前序遍历(根 左 右)](#3.1. 递归前序遍历(根 左 右))
- [3.2. 中序遍历(左 根 右)](#3.2. 中序遍历(左 根 右))
- [3.3. 后序遍历(左 右 根)](#3.3. 后序遍历(左 右 根))
- [3.4. 图示总结](#3.4. 图示总结)
- [4. 二叉树的层序遍历](#4. 二叉树的层序遍历)
- [5. 二叉树相关OJ题](#5. 二叉树相关OJ题)
-
- [5.1. 单值二叉树](#5.1. 单值二叉树)
- [5.2. 相同的树](#5.2. 相同的树)
- [5.3. 对称二叉树](#5.3. 对称二叉树)
- [5.4. 另一棵树的子树](#5.4. 另一棵树的子树)
- [6. 二叉树其他接口](#6. 二叉树其他接口)
-
- [6.1. 求二叉树的最大深度](#6.1. 求二叉树的最大深度)
- [6.2. 求二叉树的节点总数](#6.2. 求二叉树的节点总数)
- [6.3. 求第k层节点个数](#6.3. 求第k层节点个数)
- [6.4. 查找值为x的节点](#6.4. 查找值为x的节点)
- [7. 总结](#7. 总结)
1. 节点与树的基本定义
关于二叉树和树的相关概念和性质,请看这篇文章的前置知识:
我们现在直接用代码实现一个二叉树的基本结构:
cpp
// 二叉树节点结构体
template <class T>
struct tree_node {
T _val;
tree_node* _left; // 指向左子树的指针
tree_node* _right;// 指向右子树的指针
// 默认构造
tree_node(const T& val = T())
:_val(val)
, _left(nullptr)
, _right(nullptr)
{ }
};2. 手搓一个二叉树
二叉树是一种复杂的非线性结构,增删查改效率太低,我们学习二叉树是为了学习递归和分治的思想
我们用一颗固定的树来演示:
cpp
1
/ \
2 4
/ / \
3 5 6构造代码:
cpp
template <class T>
class binary_tree {
public:
typedef Node tree_node<T>;
Node* build_sample_tree() {
Node* n1 = new Node(1);
Node* n2 = new Node(2);
Node* n3 = new Node(3);
Node* n4 = new Node(4);
Node* n5 = new Node(5);
Node* n6 = new Node(6);
n1->_left = n2;
n1->_right = n4;
n2->_left = n3;
n4->_left = n5;
n4->_right = n6;
root = n1;
return root;
}
private:
Node* root;
};3. 二叉树的前中后序遍历
3.1. 递归前序遍历(根 左 右)
原理: 先处理根节点,再递归到左子树 右子树
将根节点处理完后,处理所有的左子树,再处理所有的右子树
递归三部曲: _node -> _left -> _right
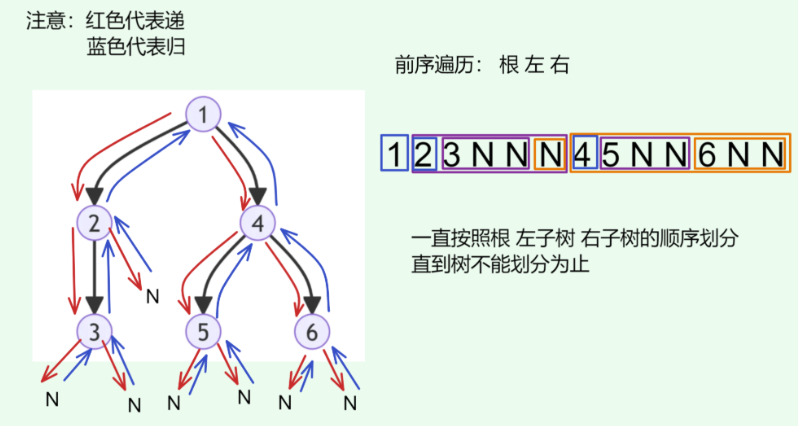
如图:
开始根1完成,往下走,
走到以2为根的树,根2,完成,往下走
走到以3为根的树,根3,完成,往下走
遇到N,3的左子树为空,回溯,回到3,开始找3的右子树,往下走
遇到N,3的右子树为空,回溯,回到3,以3为根的树遍历完成,而3是2的左孩子,回溯,回到2,开始找2的右孩子,往下走
遇到N,2的右子树为空,回溯,回到2,以w为根的树遍历完成,而2是1的左孩子,回溯,回到1,开始找1的右孩子,往下走
..............................
这体现了 "先走到尽头,再回溯继续" 的思想,前中后序都是这种思想
将复杂的一颗树不断细分,分成根-左子树-右子树,直到这个树不能再分,这便是递归的思想
- "递"表示开启新方法,程序在此过程中访问下一个节点。
- "归"表示函数返回,代表当前节点已经访问完毕。
cpp
// 前序遍历
void preorder(Node* root) const {
// 根 左 右
if (root == nullptr) {
std::cout << "N";
return;
}
// 根
cout << root->_val << " ";
// 左
preorder(root->_left);
// 右
preorder(root->_right);
}3.2. 中序遍历(左 根 右)
原理: 先左,再根,再右,二叉搜索树常用(会得到有序序列)
中序遍历按照 左子树 根 右子树的顺序
开始遇到根1,找根1的左子树,往下走
遇到根2,找根2的左子树,往下走
遇到根3,找根3的左子树,往下走
遇到N,根3的左子树找到,回溯,回到根3,开始找根3的右子树,往下走
遇到N,根3的右子树找到,回溯,回到根3,以3为根的树结束,回溯,回到根2,开始找根2的右子树
....................................
cpp
// 中序遍历 左 右 根
void inorder(Node* root) const {
if (root == nullptr) {
std::cout << "N";
return;
}
// 左
inorder(root->_left);
// 根
std::cout << root->_val << " ";
// 右
inorder(root->_right);
}3.3. 后序遍历(左 右 根)
原理: 常用来释放内存(先删子节点再删父节点)
cpp
// 后序遍历 左 右 根
void postorder(Node* root) const {
if (root == nullptr) {
std::cout << "N";
return;
}
// 左
postorder(root->_left);
// 右
postorder(root->_right);
// 根
std::cout << root->_val << " ";
}3.4. 图示总结
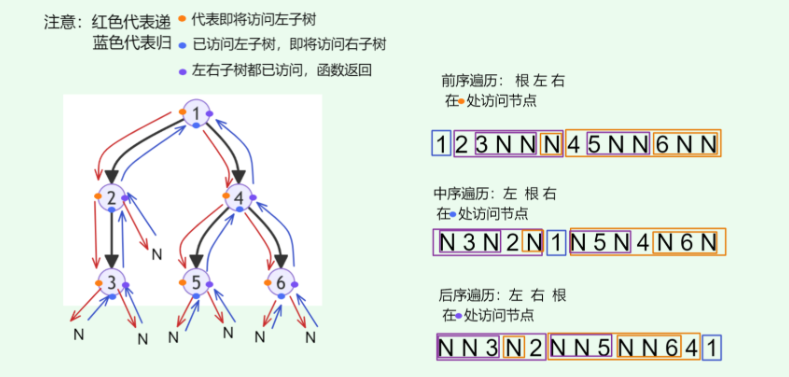
前中后序遍历都属于深度优先遍历(depth‑first traversal) ,也称深度优先搜索(depth‑first
search, DFS) ,它体现了一种 "先走到尽头,再回溯继续" 的遍历方式。
上图展示了对二叉树进行深度优先遍历的工作原理。深度优先遍历就像是绕着整棵二叉树的外围走一圈,在每个节点都会遇到三个位置,分别对应前序遍历、中序遍历和后序遍历。
4. 二叉树的层序遍历
层序遍历(Level Order Traversal)是二叉树遍历中非常特殊的一种方式:要求按照节点所在的「层次」依次访问,从根节点(第 1 层)开始,逐层向下,同一层的节点从左到右依次访问。
对于这颗树
cpp
1
/ \
2 4
/ / \
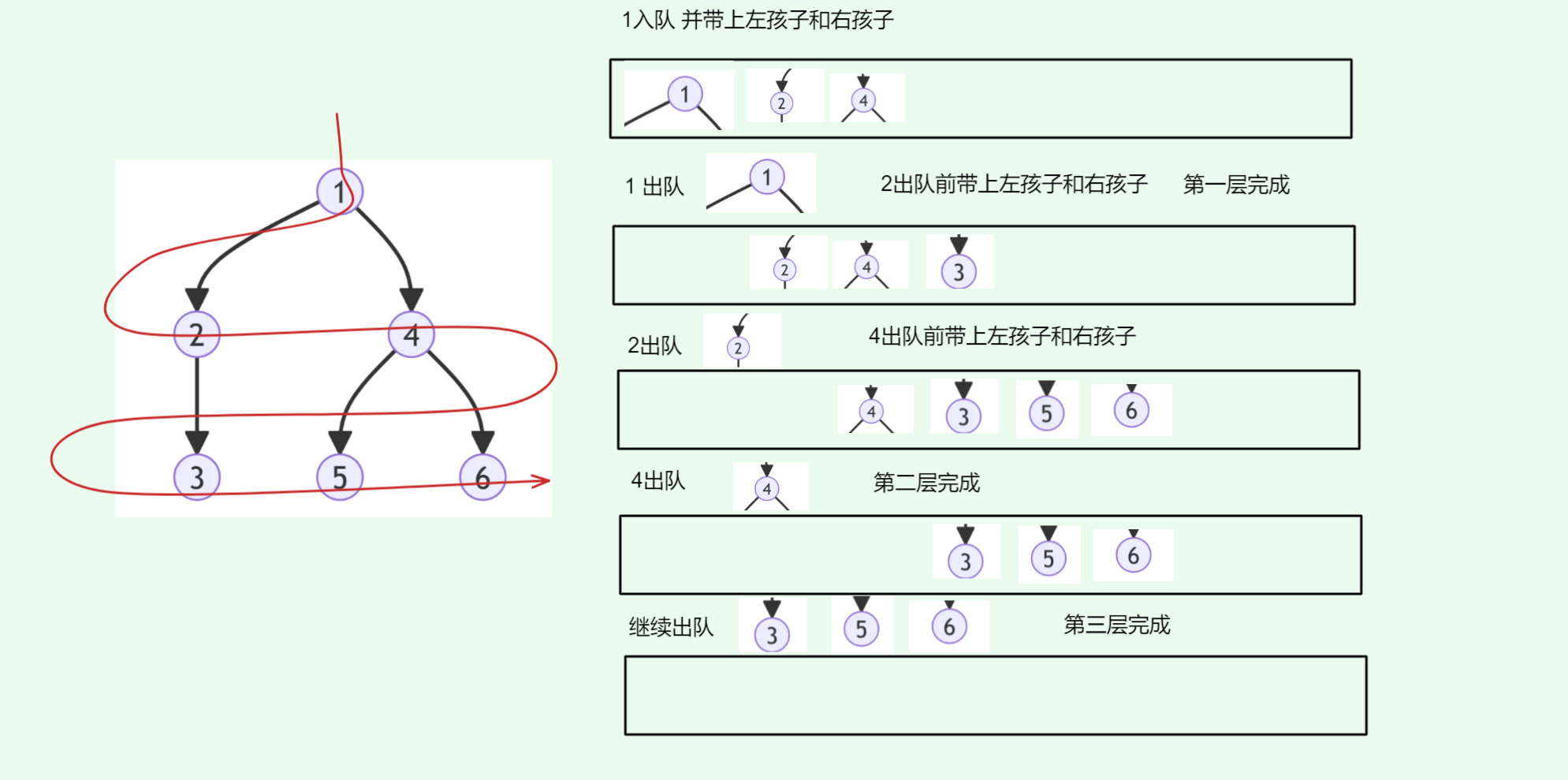
3 5 6层序遍历严格按照:1->2->4->3->5->6这样的顺序
这里的核心矛盾是:如何保证「先处理完当前层所有节点,再处理下一层」?这就是队列要解决的问题。
要实现「按层访问」,关键是要维护一个「待处理节点的顺序」,而队列的先进先出(FIFO) 特性恰好完美匹配这个需求。
只需要一层带一层即可
cpp
// 层序遍历
void level_order(Node* start) {
// 处理空节点
if (start == nullptr) return;
// 构造队列处理
std::queue<Node*> q;
q.push(start);
// 一层出队列 一层入队列 直到队列为空 遍历完成
while (!q.empty()) {
Node* cur = start;
q.pop();
std::cout << cur->_val << " ";
if(cur->_left) q.push(cur->_left);
if(cur->_right) q.push(cur->_right);
}
}5. 二叉树相关OJ题
5.1. 单值二叉树
思路:遍历二叉树,判断每个节点的值是否相同即可,值得注意的是,空树是单值二叉树
- 层序遍历,借助队列实现
cpp
class Solution {
public:
bool isUnivalTree(TreeNode* root) {
if(!root) return true;
// 层序遍历
std::queue<TreeNode*> q;
q.push(root);
int val = root->val;
while(!q.empty()){
TreeNode* cur = q.front();
q.pop();
if(!cur) continue;
if(cur->val != val)
return false;
q.push(cur->left);
q.push(cur->right);
}
return true;
}
};- 深度优先遍历,递归实现
cpp
class Solution {
public:
bool isUnivalTree(TreeNode* root) {
if(!root) return true;
// 层序遍历
std::queue<TreeNode*> q;
q.push(root);
int val = root->val;
while(!q.empty()){
TreeNode* cur = q.front();
q.pop();
if(cur->val != val) return false;
// 左子节点入队(若存在)
if (cur->left != nullptr) q.push(cur->left);
// 右子节点入队(若存在)
if (cur->right != nullptr) q.push(cur->right);
}
return true;
}
};5.2. 相同的树
思路: 两棵树走相同的路径比较路径是否相同,比较路径上的值是否相同
cpp
class Solution {
public:
bool isSameTree(TreeNode* p, TreeNode* q) {
// 走相同的路径 比较值是否相同
if(p == nullptr && q != nullptr) return false;
if(p != nullptr && q == nullptr) return false;
if(p == nullptr && q == nullptr) return true;
if(p->val != q->val) return false;
return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}
};5.3. 对称二叉树
**思路:**左子树和右子树比较,调用isSameTree就好
cpp
class Solution {
public:
bool isSymmetric(TreeNode* root) {
return isSameTree(root->left,root->right);
}
private:
bool isSameTree(TreeNode* p, TreeNode* q) {
// 走相同的路径 比较值是否相同
if(p == nullptr && q != nullptr) return false;
if(p != nullptr && q == nullptr) return false;
if(p == nullptr && q == nullptr) return true;
if(p->val != q->val) return false;
return isSameTree(p->left, q->right) && isSameTree(p->right, q->left);
}
};5.4. 另一棵树的子树
思路:
- 如果
root为空,一定没有子树,子树题目给了是不为空的 root不为空,复用isSameTree,从当前节点开始比较,当前节点比较结束之后,遍历这棵树即可,需要注意的是,对于左子树和右子树遍历,逻辑条件是或 ,因为有一棵子树和目标子树相同就相当于这个树含有SubRoot了
cpp
class Solution {
public:
bool isSubtree(TreeNode* root, TreeNode* subRoot) {
// 根会走到子树 子树为空节点 一定没有subRoot
if(!root) return false;
// 比较当前节点
if(root->val == subRoot->val && isSameTree(root,subRoot))
return true;
// 当前节点比较完成 遍历子树比较
return isSubtree(root->left,subRoot) || isSubtree(root->right,subRoot);
}
private:
bool isSameTree(TreeNode* p, TreeNode* q) {
// 走相同的路径 比较值是否相同
if(p == nullptr && q != nullptr) return false;
if(p != nullptr && q == nullptr) return false;
if(p == nullptr && q == nullptr) return true;
if(p->val != q->val) return false;
return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}
};6. 二叉树其他接口
6.1. 求二叉树的最大深度
思路:
- 最大深度是从根节点到最深叶节点的路径长度
- 对于每个节点来说:
- 空节点的深度为0
- 非空节点深度 =
max(左子树深度,右子树深度) + 1
所以可以得到代码:
cpp
// 求一棵二叉树最大深度
size_t get_depth(Node* root) {
if (!root) return 0;
// 分别求左子树和右子树的深度
size_t left_depth = get_depth(root->_left);
size_t right_depth = get_depth(root->_right);
// 更深的子树加根节点1 就是一棵树的深度
return left_depth > right_depth ? left_depth + 1 : right_depth + 1;
}6.2. 求二叉树的节点总数
思路: 一个节点的总数 = 左子树节点数 + 右子树节点数 + 当前节点本身(1)
利用分治的思想,举个例子
一个学院一个院长,两个专业,一个专业四个班,统计这个学院总共有多少人
院长将任务分发给两个专业负责人,两个专业负责人继续分发任务,给自己管理的班级再次下发任务,任务分配给四个班长,班长统计好之后,回溯 给两个专业负责人,两个负责人再回溯给院长,院长根据回溯回来的数据即可得到统计
将一个大问题不断细化,分成若干个子问题,直到子问题不可再分,解决最小子问题之后,不断回溯
cpp
// 二叉树节点数目
// 左子树节点数目 + 右子树节点数目 + 当前节点本身(1)
size_t tree_size(Node* root) {
if (!root) rteurn 0;
return tree_size(root->_left) + tree_size(root->_right) + 1;
}6.3. 求第k层节点个数
思路:
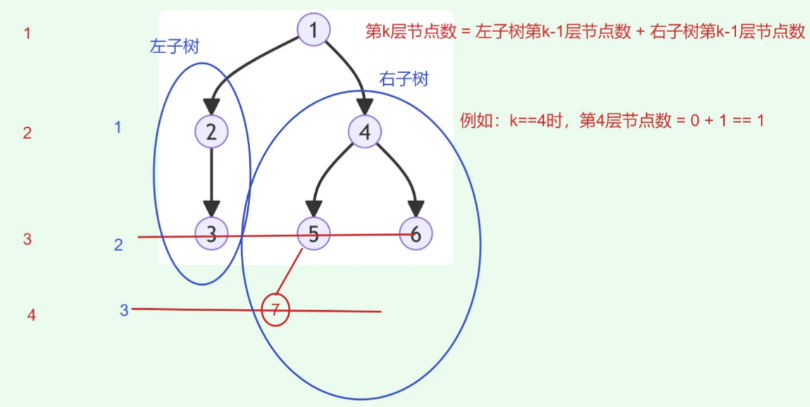
- 第1层只有根节点
- 第k层节点数 = 左子树第(k-1)层节点数 + 右子树第(k-1层)节点数
所以可以递归向下寻找,当k==1时返回1(说明当前节点就是那一层的节点)
cpp
// 第k层节点数目
size_t get_level_node_count(Node* root, size_t k) {
if (!root) return 0; // 空树
if (root != nullptr && k == 1) return 1; // 只有根节点
return get_level_node_count(root->_left, k - 1) + get_level_node_count(root->_right, k - 1);
}6.4. 查找值为x的节点
思路: 对于任意节点root
- 当前节点为空---->返回空
- 当前节点的值
==x---->找到了 - 否则,递归到左子树找,没找到,递归到右子树去找
递归的含义是:我不关心子树内部怎么找,我只关心找到了没有
cpp
// 找值为x的节点
Node* find_x(Node* root, const T& x) {
if (!root) return nullptr;
if (root->_val == x) return root;
// 递归去左子树找
Node* left = find_x(root->_left, x);
if (left) return left;
// 左子树没找到 右子树开始
return find_x(root->_right, x);
}7. 总结
通过这一章对二叉树的实现与讲解,我们从「节点结构体」出发,逐步构建了整个二叉树类的逻辑框架,真正理解了二叉树从内存组织 → 递归思想 → 遍历操作 → 内部实现机制的全过程:
- 树的本质是递归结构
每个节点既是独立的对象,又是更大结构的一部分。递归构建、递归遍历、递归销毁,都是利用了树的天然递归性。掌握这一点,就能从容理解所有树形算法。 - 节点指针与内存管理是关键
二叉树不像vector那样连续存储,而是通过指针连接节点。要时刻关注内存分配与释放,防止"野指针"和"内存泄漏"。 - 遍历是核心操作
前序、中序、后序遍历本质是访问顺序的不同:- 前序:先根 → 左子树 → 右子树
- 中序:左子树 → 根 → 右子树
- 后序:左子树 → 右子树 → 根
熟练掌握递归与非递归两种实现,是后续理解搜索树、平衡树的基础。
- 从"结构"到"抽象"
二叉树类(binary_tree)将节点操作封装起来,隐藏底层实现,让用户只需通过接口使用。这体现了封装思想 与面向对象设计的精髓。 - 从"代码"到"思维"
实现二叉树不是记语法,而是训练一种"分而治之"的思维方式:每个问题都可以被拆解为子问题,解决子问题的过程往往与整体相同。