

🔥@晨非辰Tong:个人主页
💪学习阶段:C语言、数据结构与算法初学者
⏳"人理解迭代,神理解递归。"
引言:上篇我们初探了单链表的"不连续"之美,并实现了部分基础操作。本篇将作为单链表的终极篇章,彻底攻克其余核心功能,助你构建完整知识体系。
目录
[2.5 单链表的头删](#2.5 单链表的头删)
[3.1 顺序表功能的复杂度](#3.1 顺序表功能的复杂度)
[3.2 单链表功能的复杂度](#3.2 单链表功能的复杂度)
[4.1 查找](#4.1 查找)
[4.2 在指定位置之前插入](#4.2 在指定位置之前插入)
[4.3 在指定位置之后插入](#4.3 在指定位置之后插入)
[4.4 删除pos节点](#4.4 删除pos节点)
[4.5 删除pos之后的节点](#4.5 删除pos之后的节点)
[4.6 销毁链表](#4.6 销毁链表)
二、单链表的实现(续)
2.5 单链表的头删
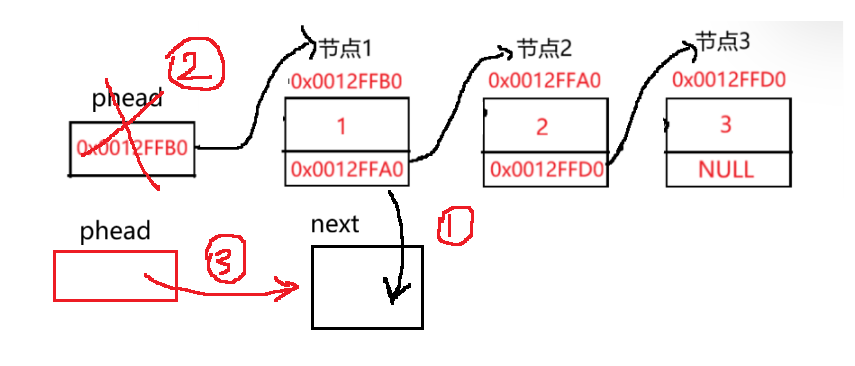
--实现头删的算法思路很简单,不同于前面实现的尾删函数:
由于定义的 phead 指向的是首节点(保存首节点的地址),就需要改变 phead 的指向--->第2节点。
那么,要定义一个新的指针 next 将第2节点的地址保存(因为释放*pphead,会将首节点next指针保存的第2节点的地址销毁),接下来直接释放首节点,再将phead指向创建的next指针(*pphead)->next = next。
cpp
SList.c文件
include "SList.h"
//定义_头删
void SLTPopFront(SLTNode** pphead)
{
//链表为空不能删除
assert(pphead && *pphead);//pphead为空--->解引用错误;*pphead为空->首节点为空(链表为空),无法删除
//定义新指针,将第2个节点第地址存起来,释放phead指向的第一个的节点
SLTNode* next = (*pphead)->next;
//释放首节点,并重新指向新指针next
free(*pphead);
//(*pphead)存放的是首节点的地址
(*pphead) = next;
}
cpp
test.c文件
include "SList.h"
void test02()
{
//创建空链表
SLTNode* phead = NULL;//phead头指针,指向的首节点为空,代表链表没有节点
//尾插
SLTPushBack(&phead, 1);//为了使形参的变化影响实参,传地址
SLTPushBack(&phead, 2);
SLTPushBack(&phead, 3);
SLTPushBack(&phead, 4);
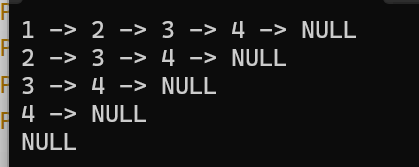
SLTPrint(phead);
//头删
SLTPopFront(&phead);
SLTPrint(phead);
SLTPopFront(&phead);
SLTPrint(phead);
SLTPopFront(&phead);
SLTPrint(phead);
SLTPopFront(&phead);
SLTPrint(phead);
}
int main()
{
test02();
return 0;
}
三、何时用顺序表,何时用单链表?
前面已经学习了如何判断算法的好坏:时间复杂度、空间复杂度!
下面通过对前面实现的顺序表、单链表插入、删除算法的复杂度计算来对比。
--复杂度主要关注时间复杂度
3.1 顺序表功能的复杂度

顺序表的尾插算法:
--程序中没有循环结构(循环次数未知),时间复杂度--->O(1)。

顺序表的头插算法:
--程序中调用了扩容函数(无循环),看函数主体------存在循环次数未知的循环结构,时间复杂度------>O(N)。

顺序表的尾删算法:
--代码没有循环结构,时间复杂度------>O(1)。

顺序表的头删算法:
--存在循环次数未知 的循环结构,时间复杂度------>O(N)。
3.2 单链表功能的复杂度
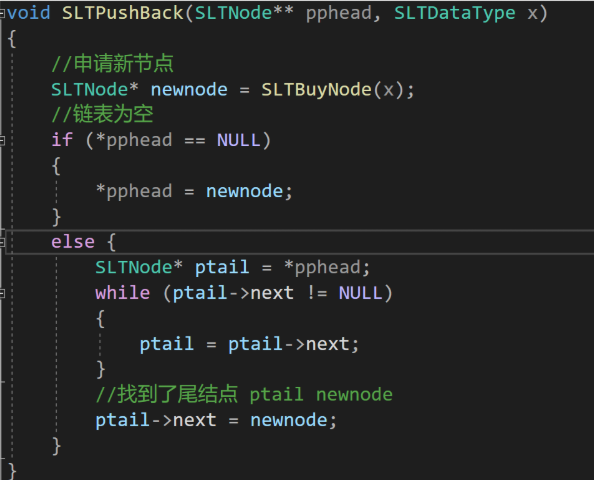
单链表的尾插算法:
--存在循环次数未知 的循环结构,时间复杂度------>O(N)。

单链表的头插算法:
--代码没有循环结构,时间复杂度------>O(1)。
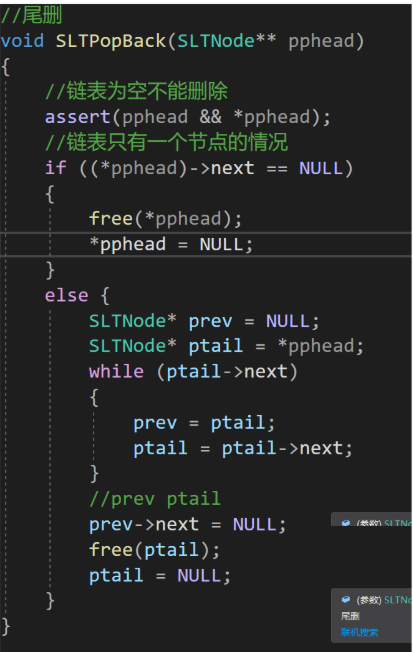
单链表的尾删算法:
--存在循环次数未知 的循环结构,时间复杂度------>O(N)。

单链表的头删算法:
--代码没有循环结构,时间复杂度------>O(1)。
通过对比发现:
- 频繁的对数据头部进行插入、删除:使用单链表;
- 频繁的对数据尾部进行插入、删除:使用顺序表。
四、链表其余功能
4.1 查找
cpp
SList.c
include "SList.c"
//定义_查找
SLTNode* SLTFind(SLTNode* phead, SLTDataType x)
{
//创建指针接收首节点
SLTNode* pcur = phead;
while (pcur)
{
if (pcur->data == x)
{
return pcur;//返回找到的数值
}
pcur = pcur->next;
}
//未找到
return NULL;//返回空
}
//返回类型为SLTNode* ,因为最后程序返回的数据是这个类型
cpp
test.c
include "SList.h"
void test02()
{
//创建空链表
SLTNode* phead = NULL;//phead头指针,指向的首节点为空,代表链表没有节点
//尾插
SLTPushBack(&phead, 1);//为了使形参的变化影响实参,传地址
SLTPushBack(&phead, 2);
SLTPushBack(&phead, 3);
SLTPushBack(&phead, 4);
SLTPrint(phead);
//查找
SLTNode* pos = SLTFind(phead, 4);
if (pos)
{
printf("找到了!\n");
}
else
{
printf("未找到!\n");
}
}
int main()
{
test02();
return 0;
}
--实现查找算法的思路很简单,需要遍历数组与目标查找数值进行对比。
4.2 在指定位置之前插入
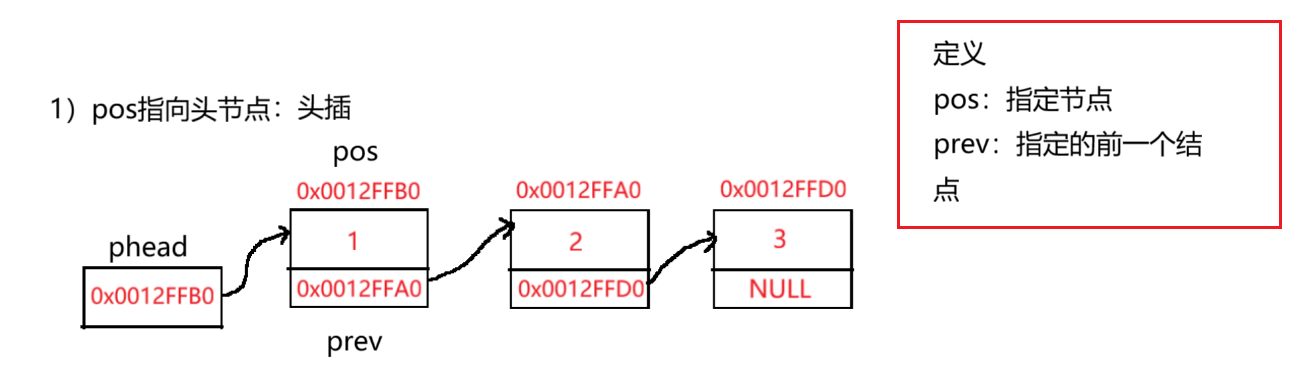
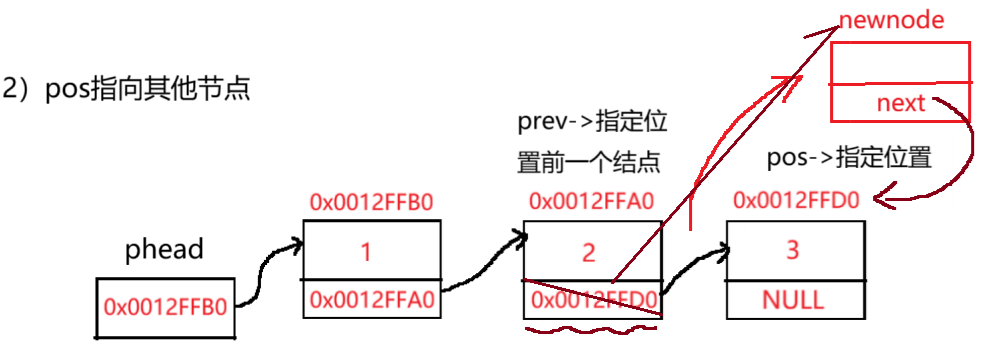
cpp
SList.c文件
include "SList.h"
//定义_在指定位置之前插入
void SLTInsert(SLTNode** pphead, SLTNode* pos, SLTDataType x)
{
assert(pphead && pos);//对二级指针解引用不能为空
//新节点存储数据
SLTNode* newcode = SLTBuyNode(x);
//pos指向头节点
if (pos == *pphead)
{
//执行头插
SLTPushFront(pphead, x);
}
else
{
//prev从首节点遍历寻找pos的前一个节点(next与pos的地址匹配)
SLTNode* prev = *pphead;
while (prev->next != pos)
{
//没找到,移动到下一个节点
prev = prev->next;
}
//跳出循环------找到了
newcode->next = pos;//新节点的next指针指向pos
prev->next = newcode;//前一个节点next指针指向新节点
}
}对于在指定位置之前插入,定义中情况为头插,涉及到首节点的改变,所以要传首节点的地址过去。
cpp
test.c文件
include "SList.h"
void test02()
{
//创建空链表
SLTNode* phead = NULL;//phead头指针,指向的首节点为空,代表链表没有节点
//尾插
SLTPushBack(&phead, 1);//为了使形参的变化影响实参,传地址
SLTPushBack(&phead, 2);
SLTPushBack(&phead, 3);
SLTPushBack(&phead, 4);
SLTPrint(phead);
SLTNode* pos = SLTFind(phead, 4);
//在4前面插入
SLTInsert(&phead, pos, 100);
SLTPrint(phead);
//在首节点前插入
pos = SLTFind(phead, 1);
SLTInsert(&phead, pos, 100);
SLTPrint(phead);
}
int main()
{
test02();
return 0;
}
4.3 在指定位置之后插入
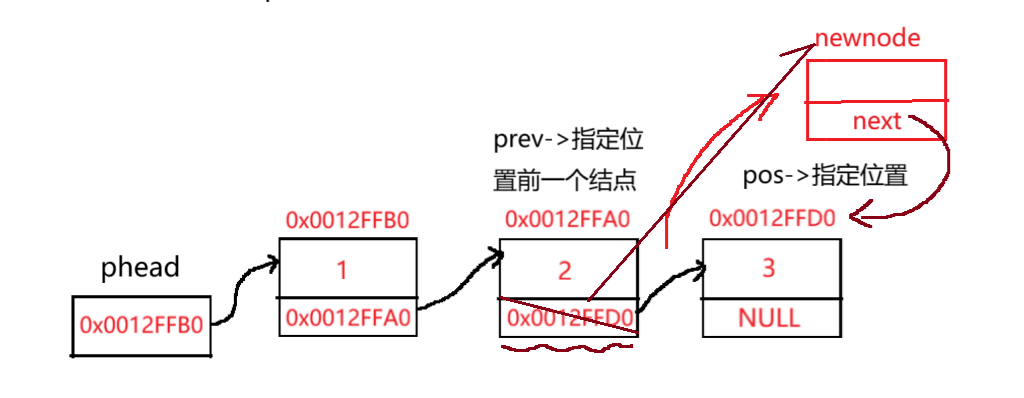
这种就是前面的第2种情况。
cpp
SList.c文件
include "SList.h"
//定义_在指定位置之后插入
SLTNode* SLTInsertAfter(SLTNode* pos, SLTDataType x)
{
assert(pos);
SLTNode* newcode = SLTBuyNode(x);
newcode->next = pos->next;//接收后节点的地址
pos->next = newcode;
}4.4 删除pos节点
cpp
SList.c文件
include "SList.h"
//定义_删除pos节点
void SLTErase(SLTNode** pphead, SLTNode* pos)
{
assert(pphead && *pphead);
//如果pos刚好就是头结点
if (pos == *pphead)
{
SLTPopFront(pphead);
}
else {
SLTNode* prev = *pphead;
while (prev->next != pos)
{
prev = prev->next;
}
//prev pos pos->next
prev->next = pos->next;
free(pos);
pos = NULL;
}
}算法思路:删除就是将节点空间释放,然后将pos前的节点与pos后的节点进行地址链接。
4.5 删除pos之后的节点
cpp
SList.c
include "SList.h"
//删除pos之后的结点
void SLTEraseAfter(SLTNode* pos)
{
assert(pos&&pos->next);
//pos del del->next
SLTNode* del = pos->next;
pos->next = del->next;
free(del);
del == NULL;
}算法思路:找到pos节点后,创建新指针接收后节点的地址,再通过next指针进行地址链接。
4.6 销毁链表
cpp
SList.c
include "SList.h"
//销毁
void SListDestroy(SLTNode** pphead)
{
assert(pphead);
SLTNode* pcur = *pphead;
while (pcur)
{
SLTNode* next = pcur->next;
free(pcur);
pcur = next;
}
*pphead = NULL;
}算法思路:只需要循环释放pos节点空间,但需要新指针先将pos之后的节点地址保存,pos再移动。
回顾:
《面试高频数据结构:单链表与顺序表之争,读懂"不连续"之美背后的算法思想》
结语:至此,我们已经为单链表这座「数据结构大厦」打下了坚实的地基。是时候解锁新的关卡了------接下来,我们将进入功能更强大的双向链表,看它如何破解单链表遍历的效率困境,让插入删除更加游刃有余。