我一直认为"网络"这个词非常贴切,因为它不仅仅指的是互联网,更广泛地涵盖了各种连接和关系的网络结构,比如社交网络、交通网络、电力网络等。在这些网络中,节点点代表实体(如人、地点、设备),而边则代表这些实体之间的连接或关系。但是,以上的这些网络,是如何构建起来的呢?
假设我们作为工程师,要在nnn个城市之间建立通讯网络,则这nnn个城市间需要最少多少条线路才能使得每个城市都能互相连通呢?显然,若是我们直接将每两个城市之间都建立一条线路,则需要的线路数为n(n−1)2\frac{n(n-1)}{2}2n(n−1),过程详见无向图最大边数计算,当nnn较大时,这个数量是非常庞大的,此时的你多半就会被炒鱿鱼了,因为很多线路都是冗余的(即多余的),我们只要保证每个城市都能互相连通即可,当城市AAA和城市BBB相连,城市BBB和城市CCC相连,那自然城市AAA与城市CCC也可以进行通信,并不需要每两个城市之间都建立一条线路。那我们如何才能在保证所有城市都能互相连通的前提下,将成本降到最低,使用最少的线路数呢?
我们在学习图的术语时得知,一个连通图的生成树是一个包含图中所有顶点的极小连通子图 ,我们还得知,它拥有图中所有顶点,但恰好只包含确保连通所需的最少边数,即对于一个有nnn个顶点的连通图,它的生成树包含n−1n-1n−1条边。那我们只要找到这个连通图的生成树,就能解决我们的问题了。但是我们现在面对的是有代价的边,即我们面对的图是带权图,而生成树并没有考虑边的权值,所以我们需要找到一种特殊的生成树,它不仅包含图中所有顶点,且边数最少,同时还要使得所有边的权值之和最小,这样一来,我们就能以最低的成本连接所有城市,这种特殊的生成树被称为最小代价生成树(Minimum Cost Spanning Tree) ,简称最小生成树(Minimum Spanning Tree, MST)。
首先我们给出部分约定:
- 只考虑连通图:当一个图是非连通图时,我们也只能找出它的连通分量的最小生成树,因为未被连通的顶点连过去的边都没有,谈何代价,更没有最小可言。
- 边的权重都不相同:作为以教学为目的的文章,我们不用太过于类似现实考虑多边权重一致的情况,这样的情况下产生的最小生成树可能不唯一,会增加理解难度。
接下来我们先认识一个获得最小生成树的经典算法------Prim算法。
1、普里姆(Prim)算法
既然我们要构造一个最小生成树,那我们就需要一个起点,又由于我们的最小生成树肯定是包含图中所有顶点的,那我们可以从图中的任意一个顶点开始,然后逐步扩展,直到包含所有顶点为止。假设我们给出如下这张带权图:
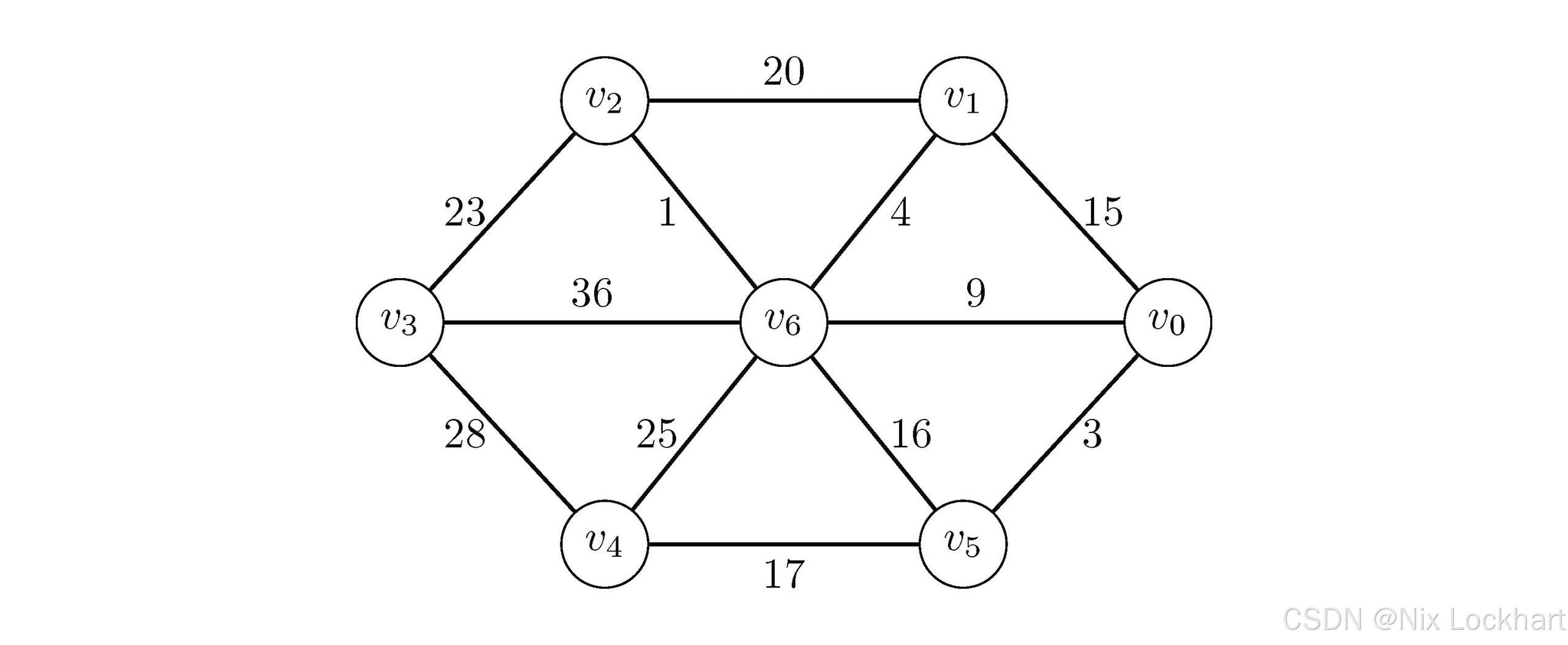
图1:一个带权图
就从顶点v0v_0v0开始,那该如何进行边的选择呢?既然我们最终构造的生成树是包含所有顶点的,也就是说我们肯定会走遍每个结点,不妨提出以下策略:
- 从当前已构造出的部分生成树中,选择一条权值最小的边(u,v)(u,v)(u,v),其中uuu是当前生成树中的顶点,而vvv是当前生成树外的顶点。
- 将边(u,v)(u,v)(u,v)和顶点vvv加入到当前生成树中。
- 重复上述过程,直到生成树中包含了图中的所有顶点为止。
这个策略实际上就是Prim算法的核心思想。我们来具体分析一下这个过程:
注:下面的过程中,我们用黑色顶点表示已经加入生成树的顶点,黑色边表示已经加入生成树的边;红色边表示当前可选择的边。
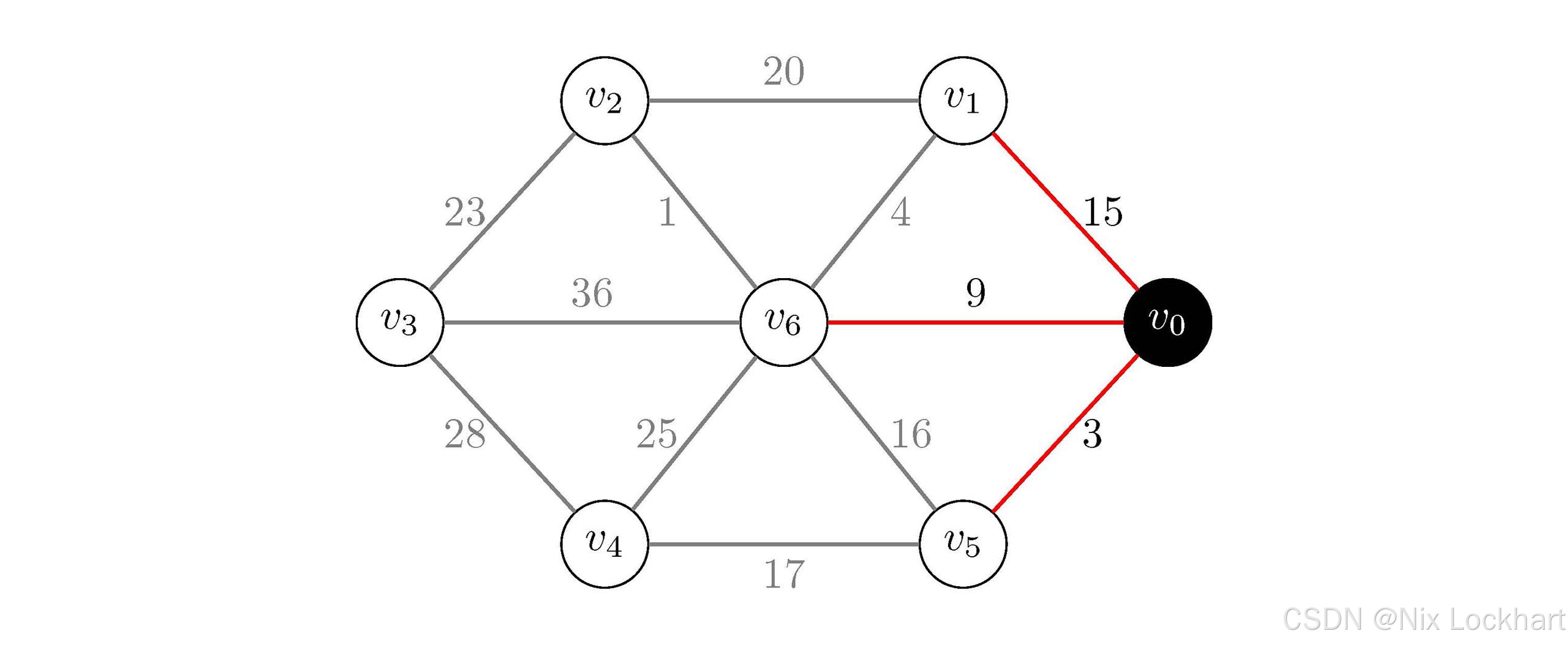
图2:Prim算法过程1
首先我们从顶点v0v_0v0开始,当前生成树中只有v0v_0v0,然后我们查看与v0v_0v0相连的边,发现有两条边(v0,v1)(v_0,v_1)(v0,v1)、(v0,v5)(v_0,v_5)(v0,v5)和(v0,v6)(v_0,v_6)(v0,v6),它们的权值分别为15、3和9,根据我们提出的策略选择权值最小的边(v0,v5)(v_0,v_5)(v0,v5),将其与顶点v5v_5v5加入生成树中,如下:
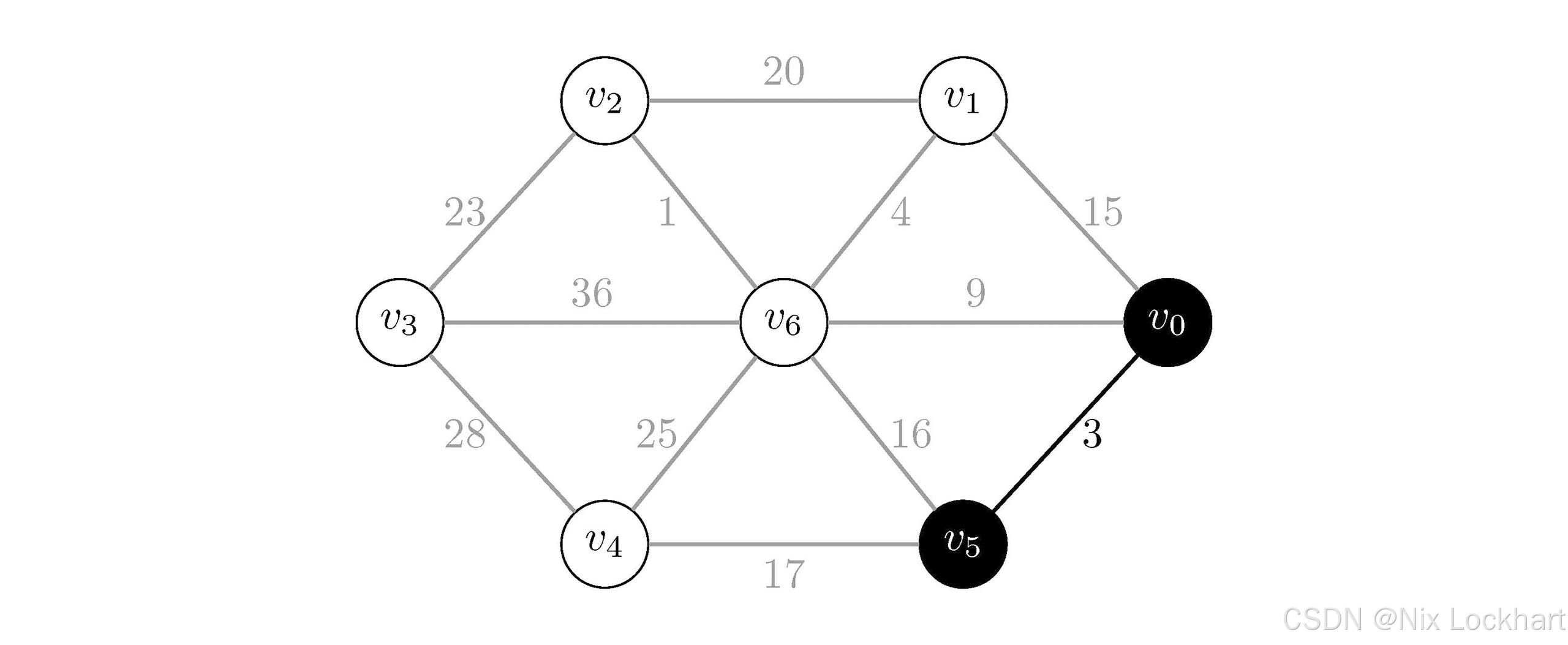
图3:Prim算法过程2
现在我们的生成树中有顶点{v0,v5}\{v_0,v_5\}{v0,v5}和边{(v0,v5)}\{(v_0,v_5)\}{(v0,v5)}。
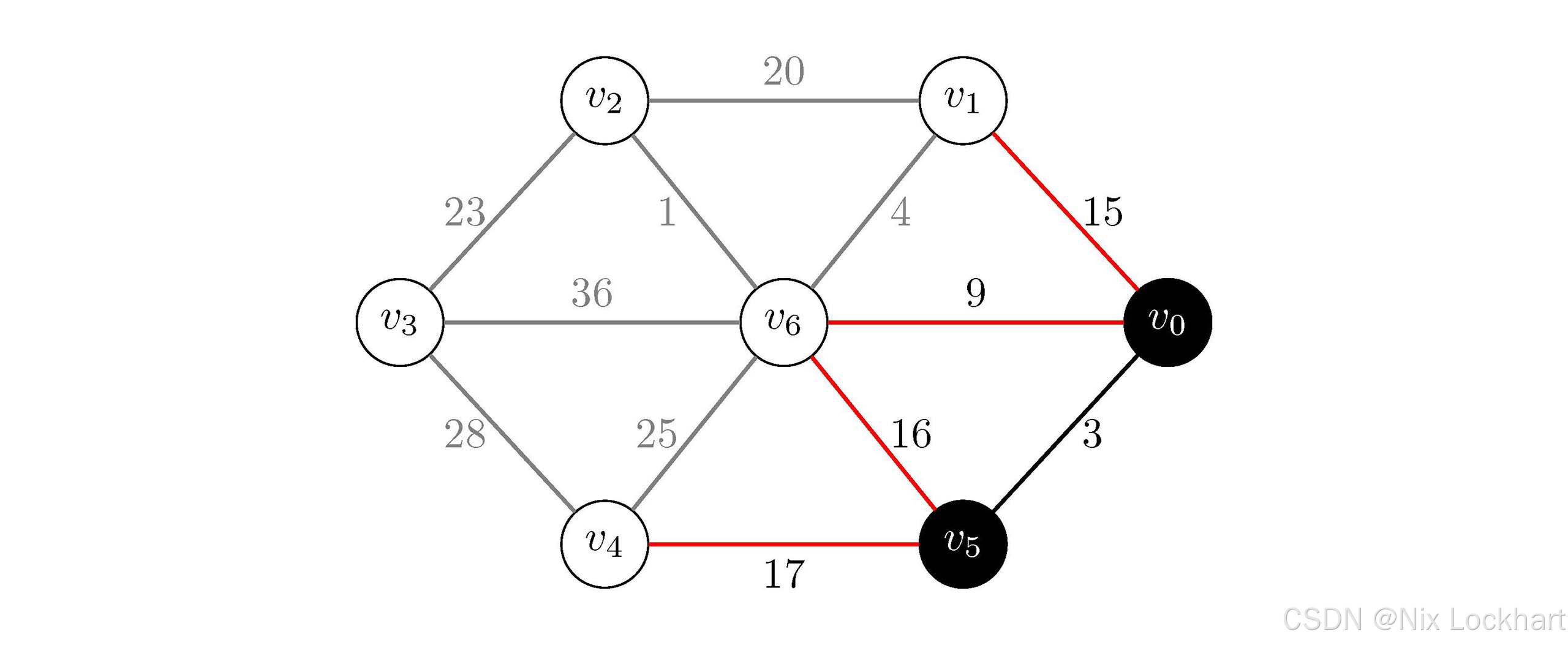
图4:Prim算法过程3
然后我们查看与当前生成树中顶点相连的边,发现有四条边(v0,v1)(v_0,v_1)(v0,v1)、(v0,v6)(v_0,v_6)(v0,v6)、(v5,v4)(v_5,v_4)(v5,v4)和(v5,v6)(v_5,v_6)(v5,v6),它们的权值分别为15、9、17和16,根据策略选择权值最小的边(v0,v6)(v_0,v_6)(v0,v6),将其与顶点v6v_6v6加入生成树中。
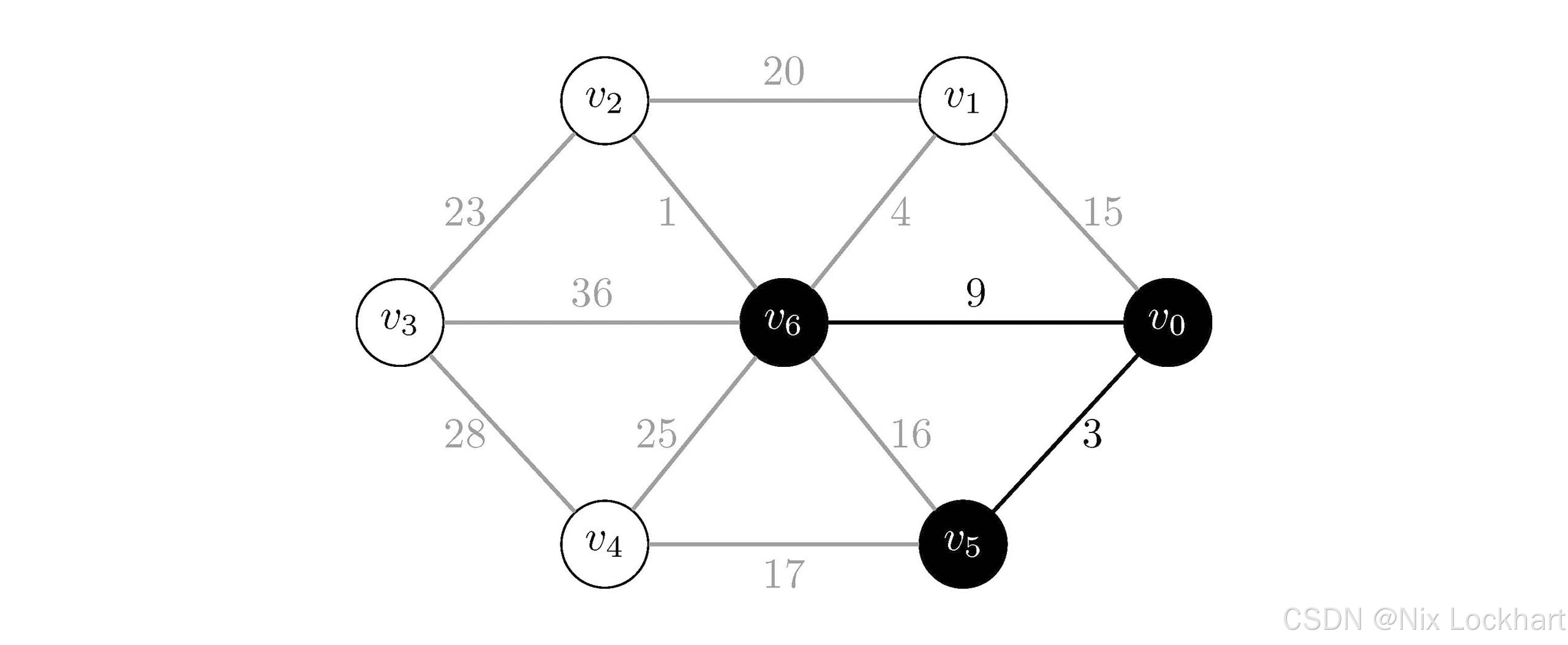
图5:Prim算法过程4
现在我们的生成树中有顶点{v0,v5,v6}\{v_0,v_5,v_6\}{v0,v5,v6}和边{(v0,v5),(v0,v6)}\{(v_0,v_5),(v_0,v_6)\}{(v0,v5),(v0,v6)}。
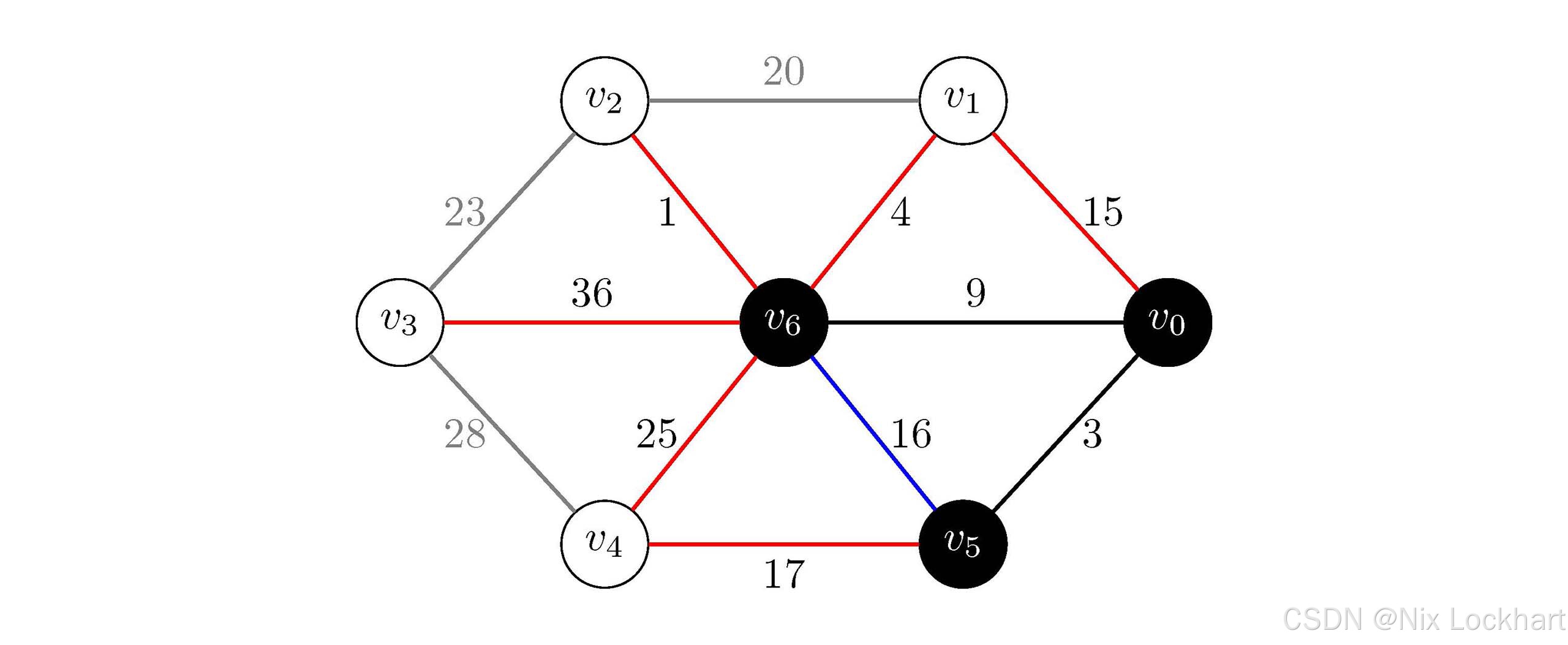
图6:Prim算法过程5
接下来再看与当前生成树中顶点相连的边,多出来许多边,有(v0,v1)(v_0,v_1)(v0,v1)、(v5,v4)(v_5,v_4)(v5,v4)、(v6,v1)(v_6,v_1)(v6,v1)、(v6,v2)(v_6,v_2)(v6,v2)、(v6,v3)(v_6,v_3)(v6,v3)、(v6,v4)(v_6,v_4)(v6,v4),除以上边以外,还有一条边(v5,v6)(v_5,v_6)(v5,v6),但是它连接的两个顶点都已经在生成树中了,所以我们不再考虑它(后续均使用蓝色标识这种边)。上述其余边的权值分别为15、17、4、1、36和25,择权值最小的边(v6,v2)(v_6,v_2)(v6,v2),将其与顶点v2v_2v2加入生成树中。
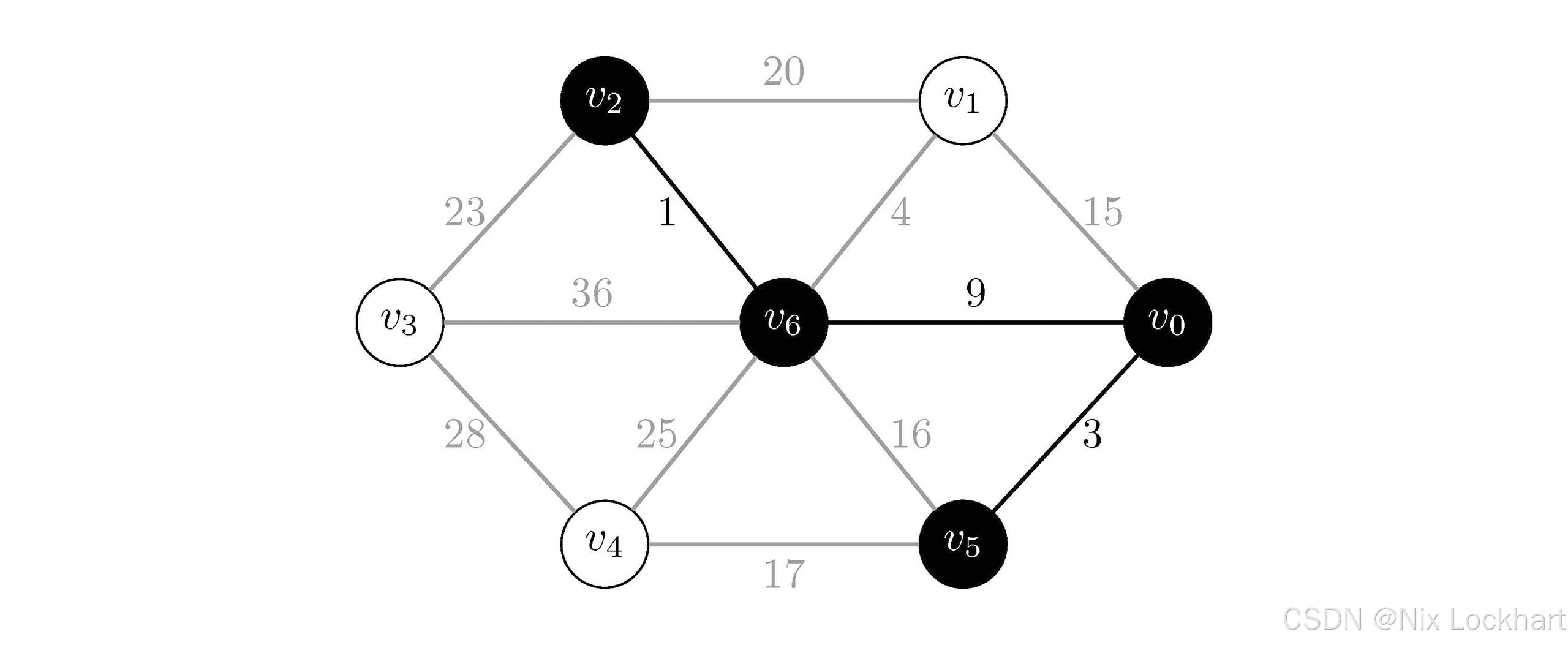
图7:Prim算法过程6
现在我们的生成树中有顶点{v0,v5,v6,v2}\{v_0,v_5,v_6,v_2\}{v0,v5,v6,v2}和边{(v0,v5),(v0,v6),(v6,v2)}\{(v_0,v_5),(v_0,v_6),(v_6,v_2)\}{(v0,v5),(v0,v6),(v6,v2)}。
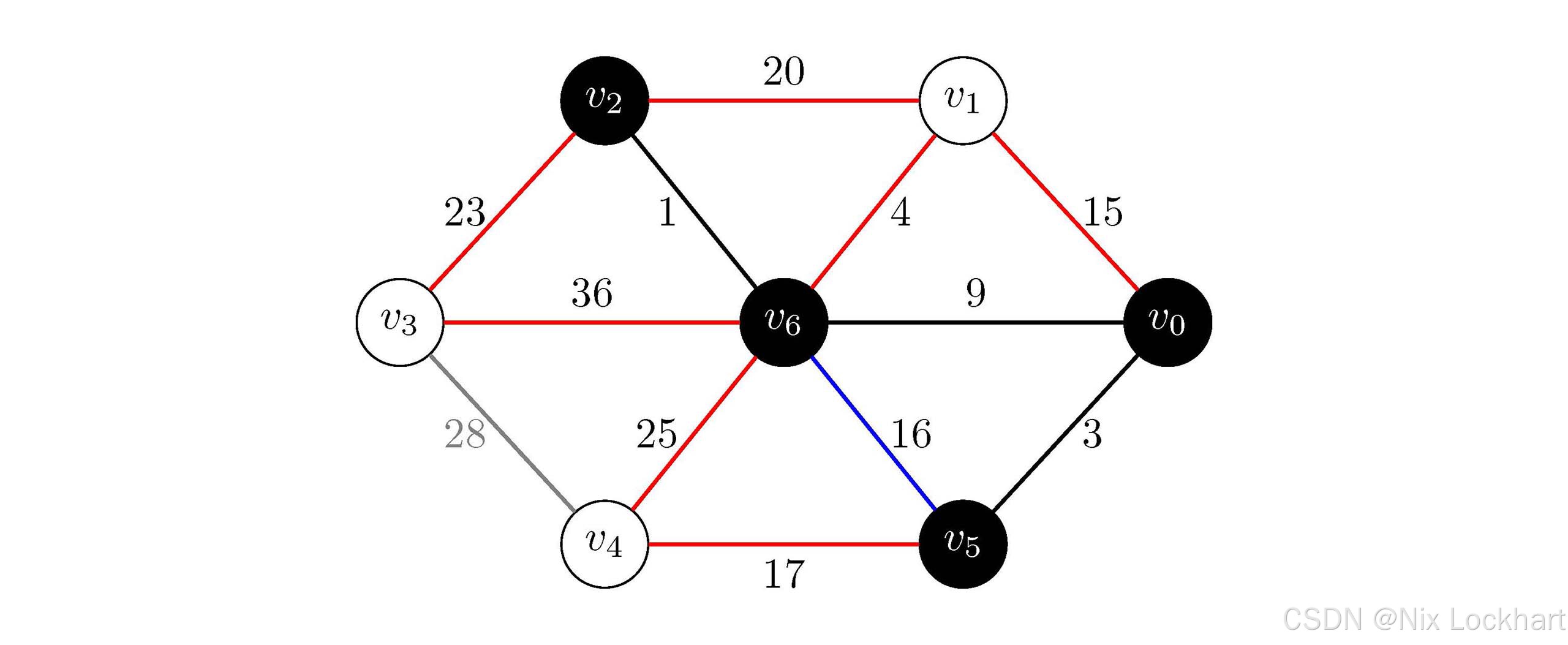
图8:Prim算法过程7
与上面相同的思路,我们选择边(v6,v1)(v_6,v_1)(v6,v1)并将顶点v1v_1v1加入生成树中。后续过程不再叙述,只给出示意图:
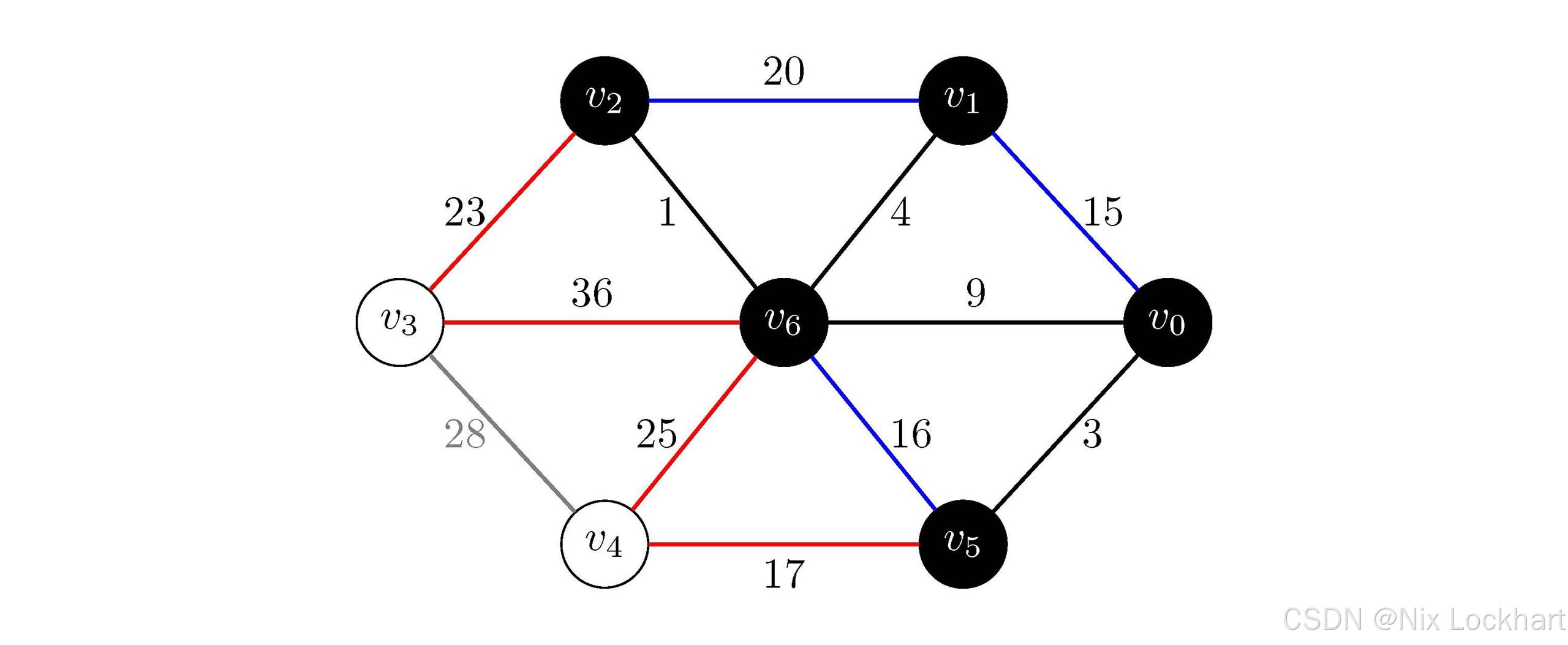
图9:Prim算法过程8
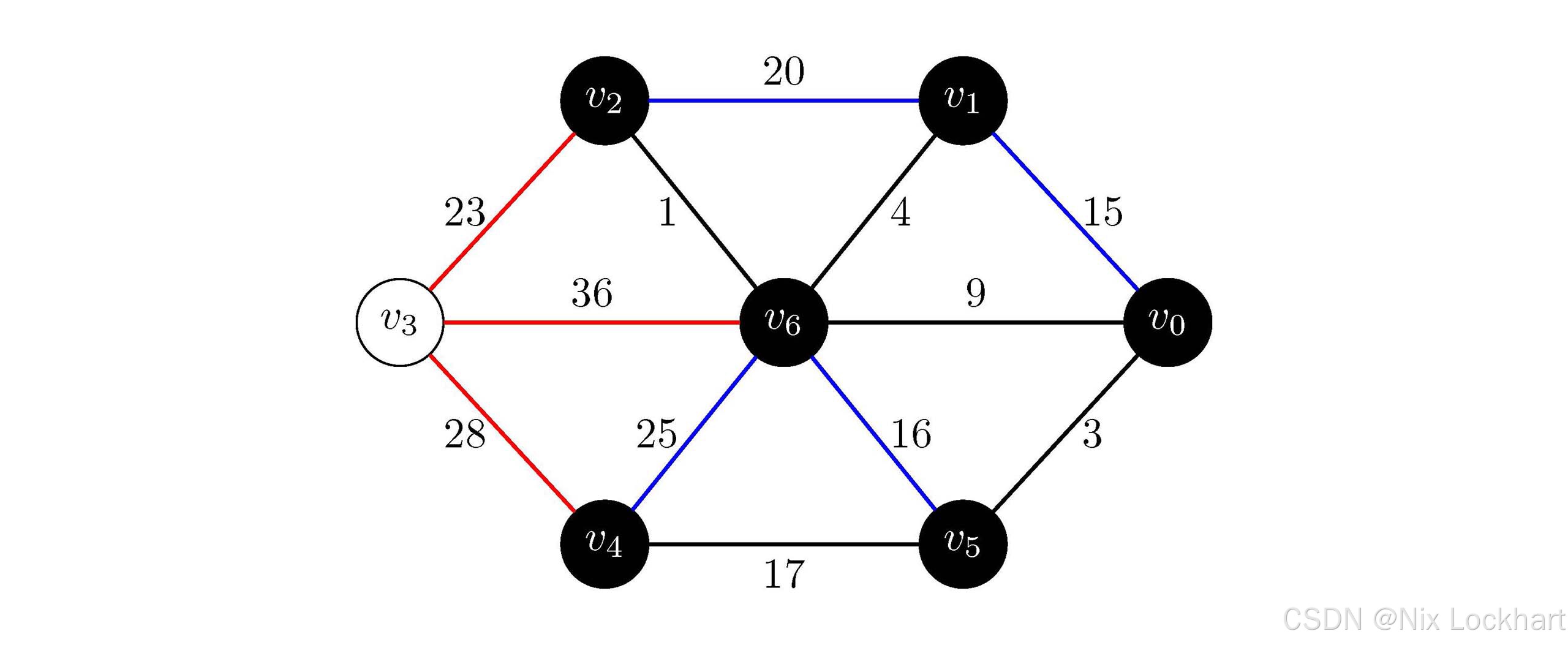
图10:Prim算法过程9
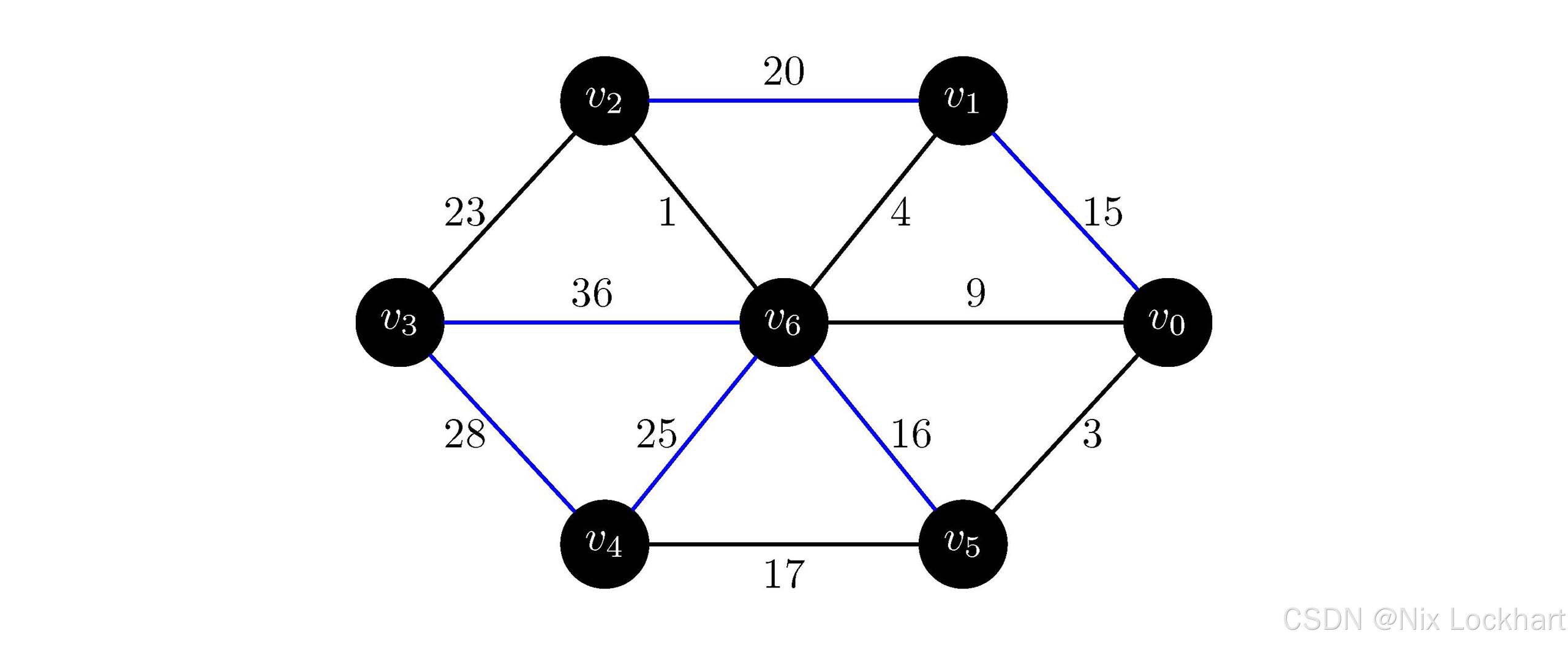
图11:Prim算法过程10
此时我们的生成树中已经包含了图中的所有顶点,算法结束。
最终我们得到的最小生成树如下:
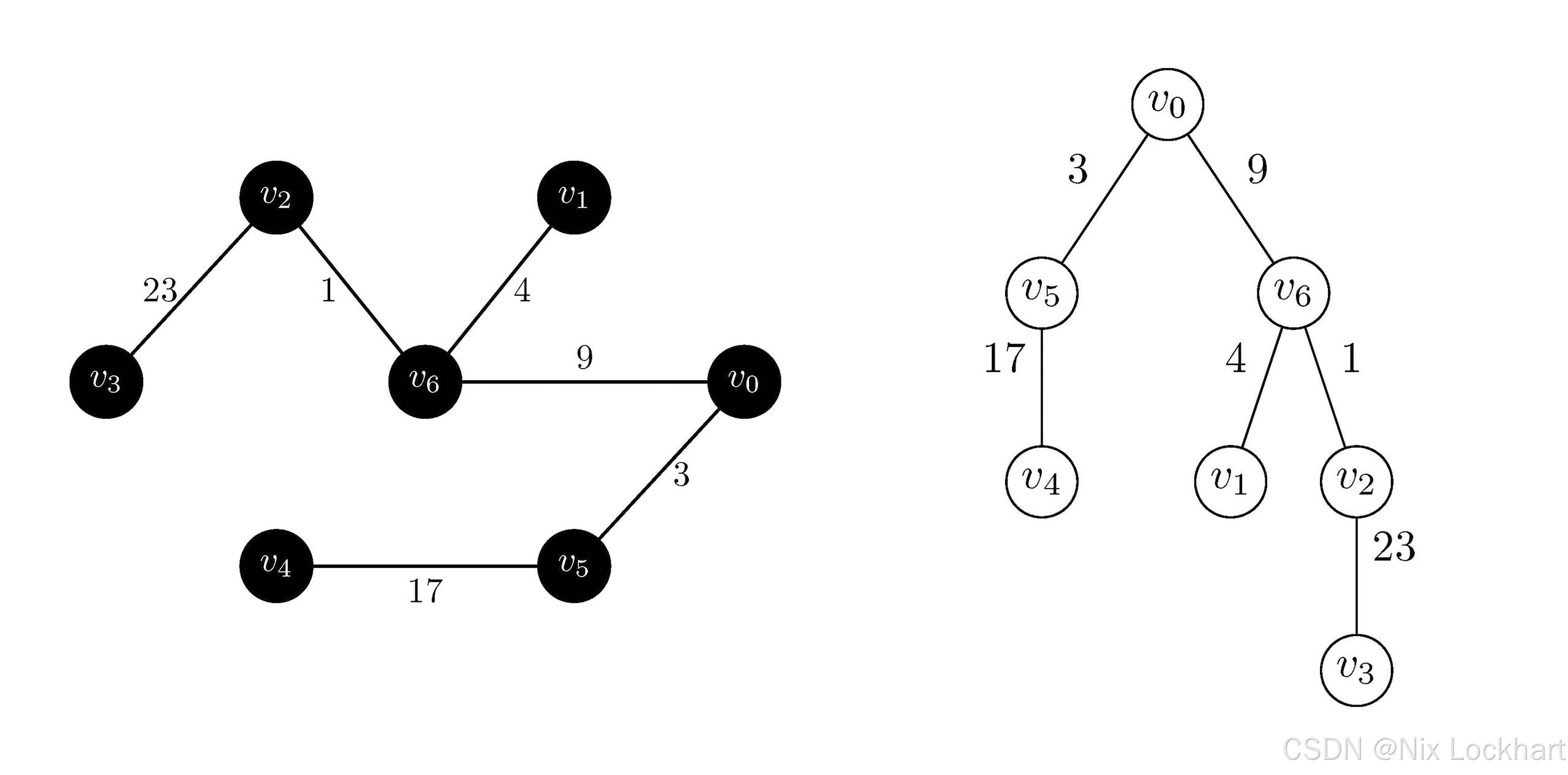
图12:Prim算法结果
大家可以检查一下,发现该生成树中包含了图中的所有顶点,且边数为顶点数减一,且是所有可能的生成树中权值之和最小的,所以它确实是该图的最小生成树。
接下来我们给出Prim算法的邻接矩阵存储结构实现代码:
c
#define MAXVEX 100 // 最大顶点数
#define INFINITY 65535 // 用于表示无穷大
void Prim(GraphAdjMatrix G, int start) // 从顶点start出发构造最小生成树
{
int min, i, j, k;
int adjvex[MAXVEX]; // 保存相关顶点下标
int lowcost[MAXVEX]; // 保存相关顶点间边的权值
// 初始化
for (i = 0; i < G.numVertexes; i++)
{
lowcost[i] = G.arc[start][i]; // 将起始顶点到各顶点的权值存入数组
adjvex[i] = start; // 初始化相关顶点为起始顶点
}
lowcost[start] = 0; // 起始顶点加入生成树
// 构造最小生成树
for (i = 0; i < G.numVertexes; i++)
{
min = INFINITY; // 初始化最小权值为无穷大
j = 0;
k = 0;
while (j < G.numVertexes) // 找到权值最小的边
{
if (lowcost[j] != 0 && lowcost[j] < min)
{
min = lowcost[j];
k = j;
}
j++;
}
printf("(%c, %c) ", G.vexs[adjvex[k]], G.vexs[k]); // 输出边
lowcost[k] = 0; // 标记该顶点已加入生成树
// 更新相关顶点和权值数组
for (j = 0; j < G.numVertexes; j++)
{
// 如果顶点j不在生成树中,且边(k,j)的权值小于当前顶点j的权值
if (lowcost[j] != 0 && G.arc[k][j] < lowcost[j])
{
lowcost[j] = G.arc[k][j]; // 更新权值
adjvex[j] = k; // 更新相关顶点
}
}
}
}我们先给出之前图的邻接矩阵:
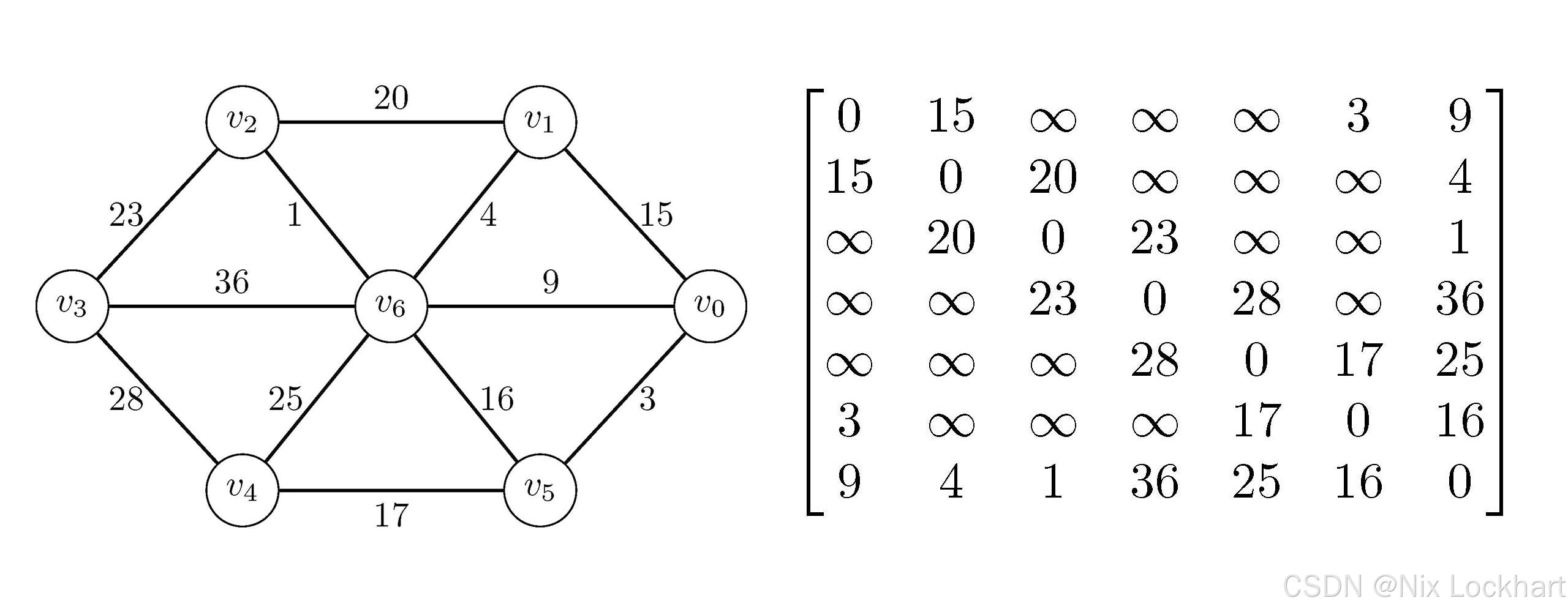
图13:带权图的邻接矩阵
代码理解起来要比我们上面所提出的过程要复杂一点,我们再来简单分析一下调用Prim(G, 0)的代码执行过程:
- 首先我们在代码第7~8行初始化了两个数组
adjvex和lowcost,其中adjvex[i]表示当前生成树中与顶点iii相连的顶点,而lowcost[i]表示当前生成树中到顶点iii的边的权值。 - 在第11行,我们使用一个
0~numVertexes-1的循环来进行初始化,将起始顶点到各顶点的权值存入lowcost数组中;然后将adjvex数组初始化为起始顶点,表示当前生成树中所有顶点都与起始顶点相连,并在循环之后将lowcost[start]设为0,表示起始顶点已经加入生成树中。
从这里我们就大致能理解数组lowcost和adjvex的含义了,lowcost[i]表示当前生成树中到顶点iii的边的权值,若lowcost[i]为0,则表示顶点iii已经加入生成树中;adjvex[i]表示当前生成树中与顶点iii直接相连的顶点。若是还不理解也没有关系,我们可以继续往下看。
当第11行的循环结束后,我们得到:
lowcost[]=[0,15,∞,∞,∞,3,9]lowcost[]=[0,15,\infty,\infty,\infty,3,9]lowcost[]=[0,15,∞,∞,∞,3,9] adjvex[]=[0,0,0,0,0,0,0]adjvex[]=[0,0,0,0,0,0,0]adjvex[]=[0,0,0,0,0,0,0]
- 然后就是第19行开始的一个大循环了,这个循环的作用就是执行我们上面所提出的Prim算法的核心思想,循环
numVertexes-1次,每次加入一条边和一个顶点。 - 第21~23行,初始化了
min、j和k,其中min表示当前找到的最小权值(将其初始化为无穷大,以方便后续比较),j表示当前检查的顶点下标,k表示当前找到的最小权值对应的顶点下标。 - 接下来第24~29行的
while循环就是在寻找当前生成树中到未加入生成树的顶点的边中权值最小的边了,循环变量j从0开始,若lowcost[j]不为0且小于当前min,则更新min和k,直到循环结束,我们就找到了当前生成树中某顶点到未加入生成树的顶点的边中权值最小的边。例如,我们从j=0开始,发现lowcost[0]=0,不符合条件;继续j=1,发现lowcost[1]=15,符合条件,则更新min=15和k=1,继续j=2,发现lowcost[2]=65535,不符合条件,继续j=3,4同理不符合条件,继续j=5,发现lowcost[5]=3,符合条件,则更新min=3和k=5,继续j=6,发现lowcost[6]=9,不符合条件,循环结束,我们找到了当前生成树中到未加入生成树的顶点的边中权值最小的边为(v0,v5)(v_0,v_5)(v0,v5)。
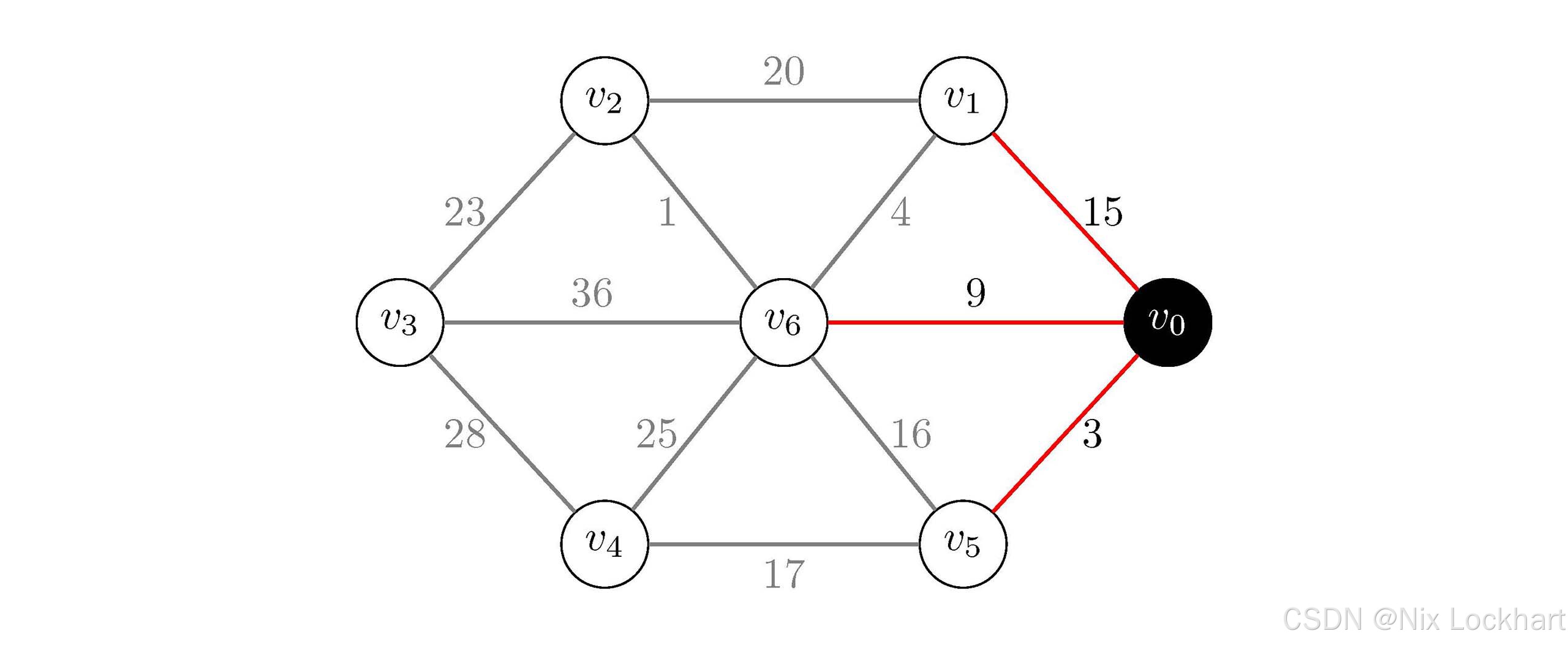
图14:Prim代码分析过程示意
- 第30行,我们输出这条边(v0,v5)(v_0,v_5)(v0,v5),然后在第31行将
lowcost[5]设为0,表示顶点v5v_5v5已经加入生成树中。 - 接下来第34~42行的
for循环就是在更新lowcost和adjvex数组了,我们遍历所有顶点,若顶点vjv_jvj不在生成树中(即lowcost[j] != 0),且边(vk,vj)(v_k,v_j)(vk,vj)的权值小于当前顶点vjv_jvj的代价(即G.arc[k][j] < lowcost[j]),则更新lowcost[j]和adjvex[j]。例如,此时我们有k=5,我们从j=0开始,发现lowcost[0]=0,不符合条件;继续j=1时有lowcost[1]=15,而G.arc[5][1]=65535不符合G.arc[k][j] < lowcost[j]条件,继续j=2,3,发现目前生成树中还是没有办法到达v2v_2v2和v3v_3v3,即G.arc[5][2,3]=65535且lowcost[2,3]=65535,不符合条件,继续j=4,我们发现lowcost[4]=65535但G.arc[5][4]=17,也就是说,我们找到了当前生成树到达顶点v4v_4v4的更短方案,于是我们用刚找出的更短方案G.arc[5][4]来替换lowcost[4],并且将能到达v4v_4v4的生成树中顶点存为v5v_5v5(即adjvex[4]=5),继续j=6,发现lowcost[6]=9且边(v5,v6)(v_5,v_6)(v5,v6)的权值为16,不符合条件,循环结束,我们得到:
lowcost[]=[0,15,∞,∞,17,0,9]lowcost[]=[0,15,\infty,\infty,17,0,9]lowcost[]=[0,15,∞,∞,17,0,9] adjvex[]=[0,0,0,0,5,0,0]adjvex[]=[0,0,0,0,5,0,0]adjvex[]=[0,0,0,0,5,0,0]
这样,构造生成树的一轮大循环就结束了,接下来进入下一轮大循环,重复上述过程,直到生成树中包含了图中的所有顶点为止,不再进行详解,接下来给出每一步的示意图和数组内容。
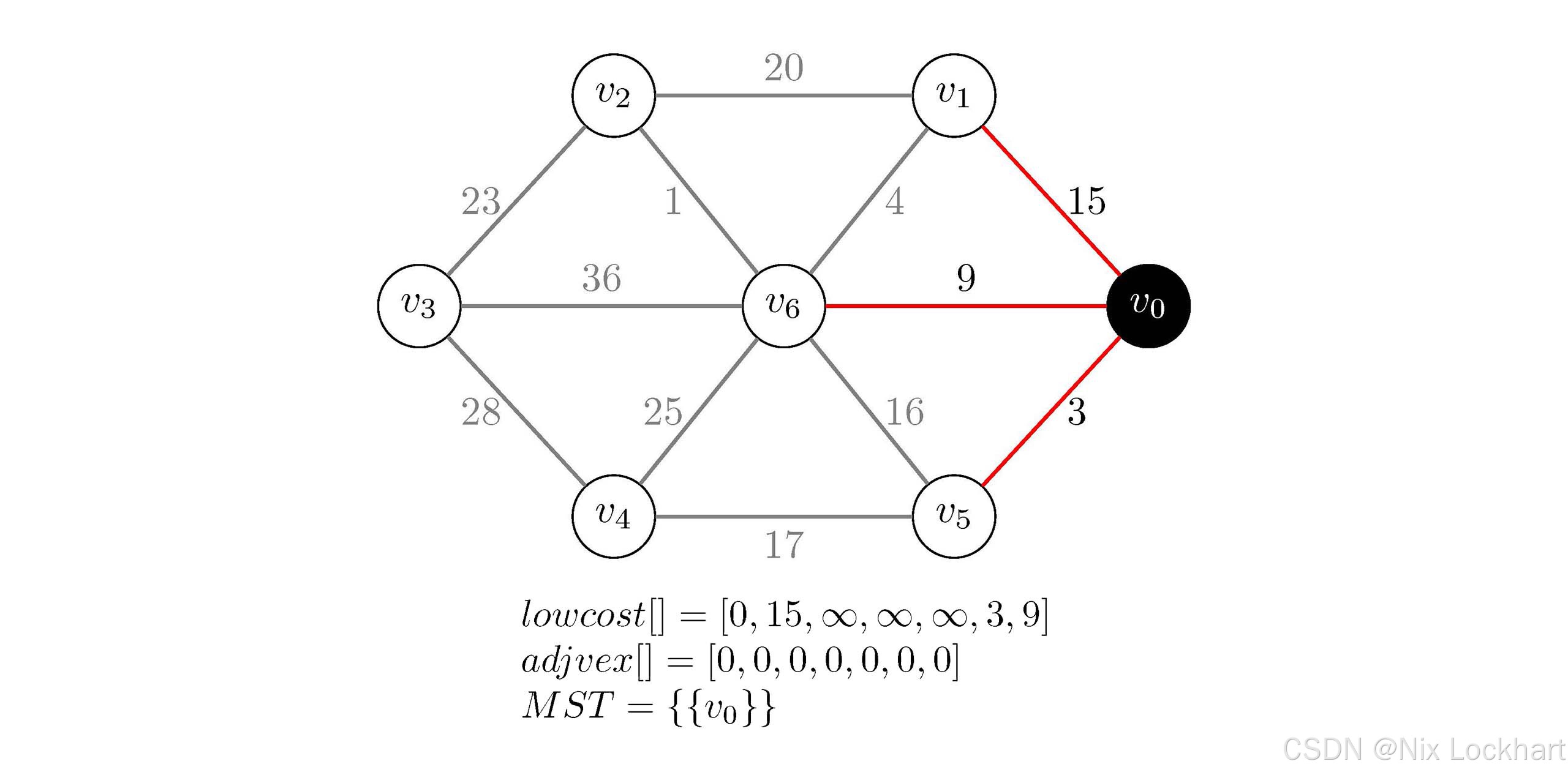
图15:Prim代码执行过程示意1
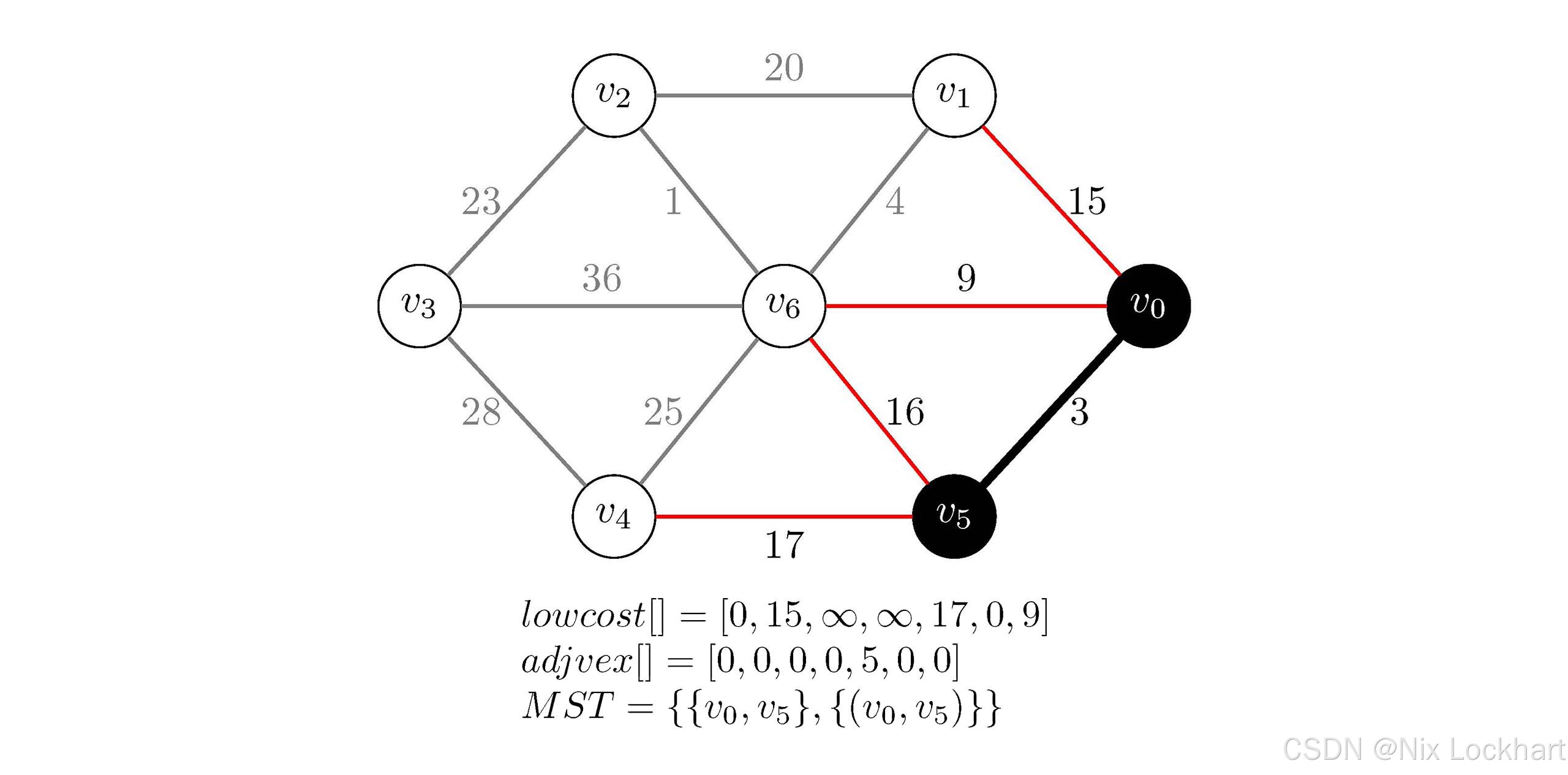
图16:Prim代码执行过程示意2
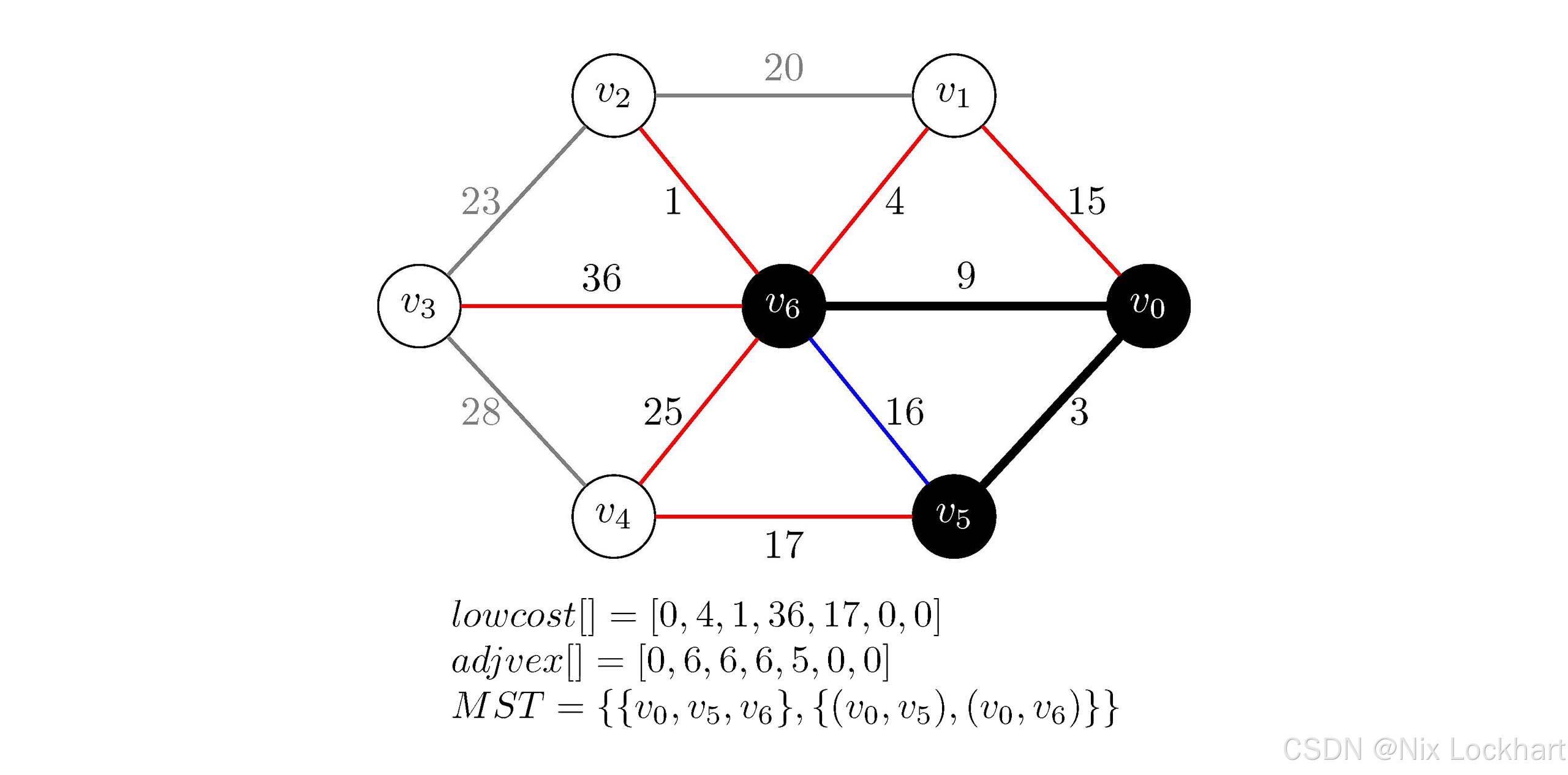
图17:Prim代码执行过程示意3
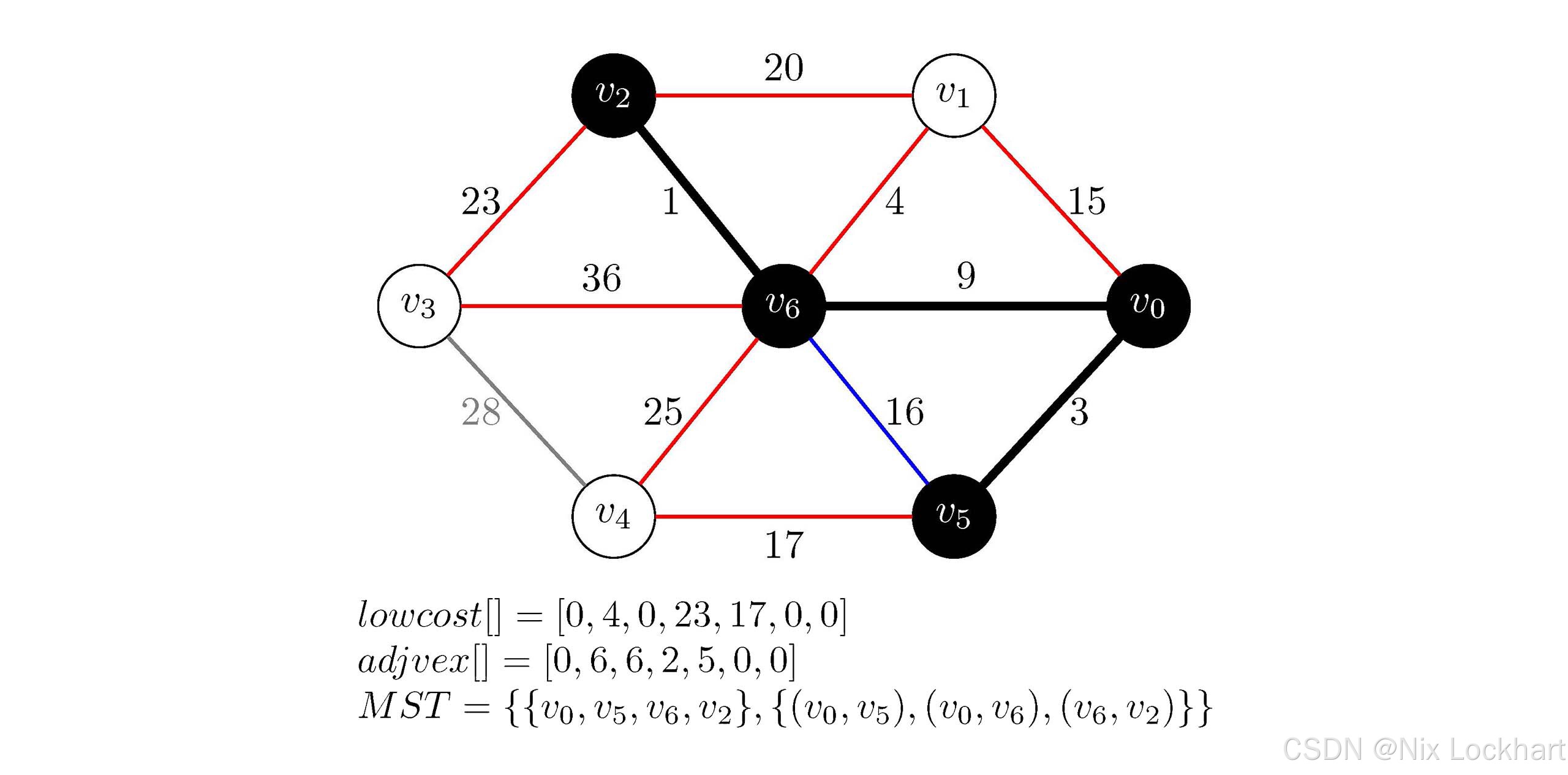
图18:Prim代码执行过程示意4
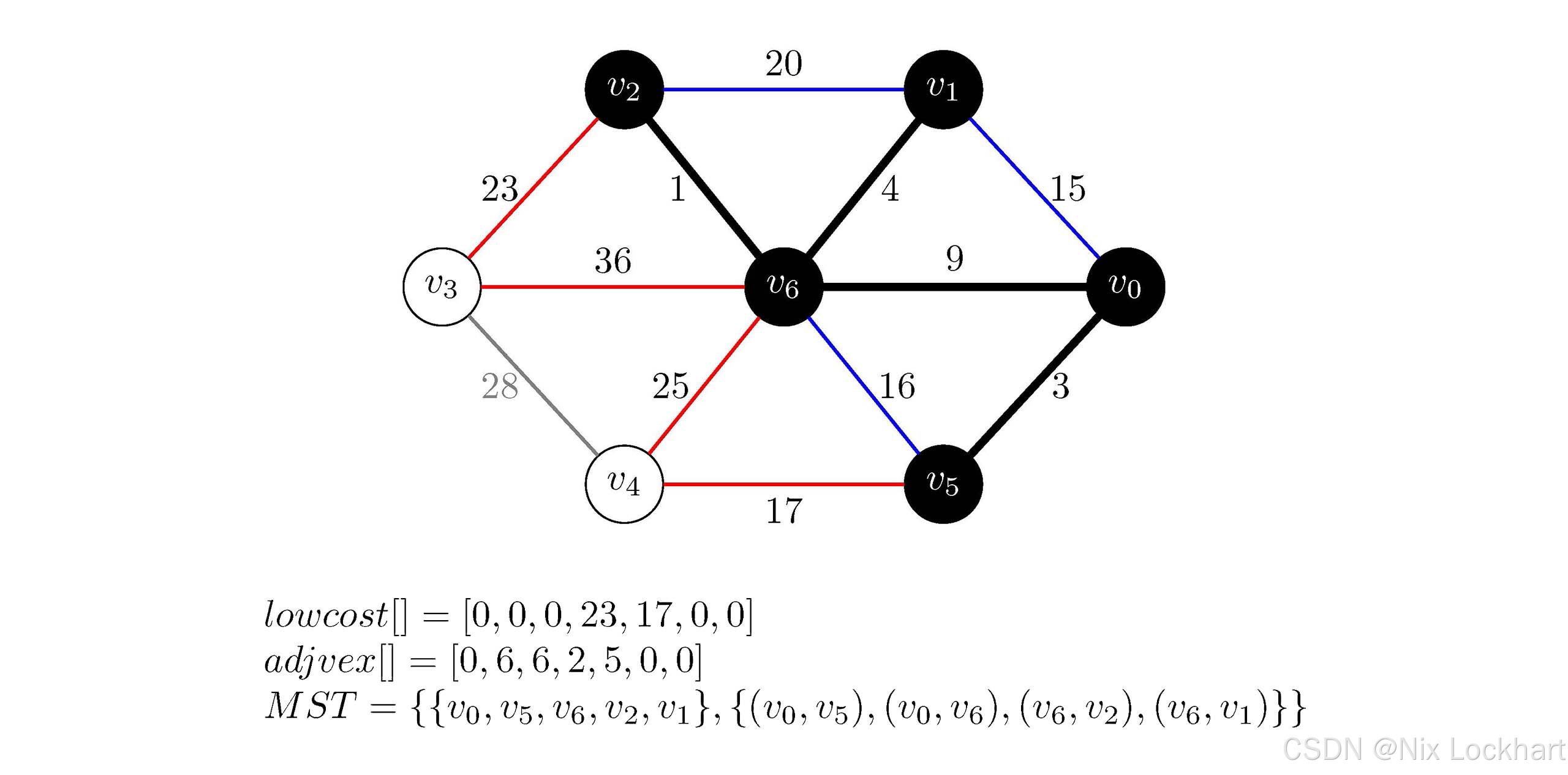
图19:Prim代码执行过程示意5
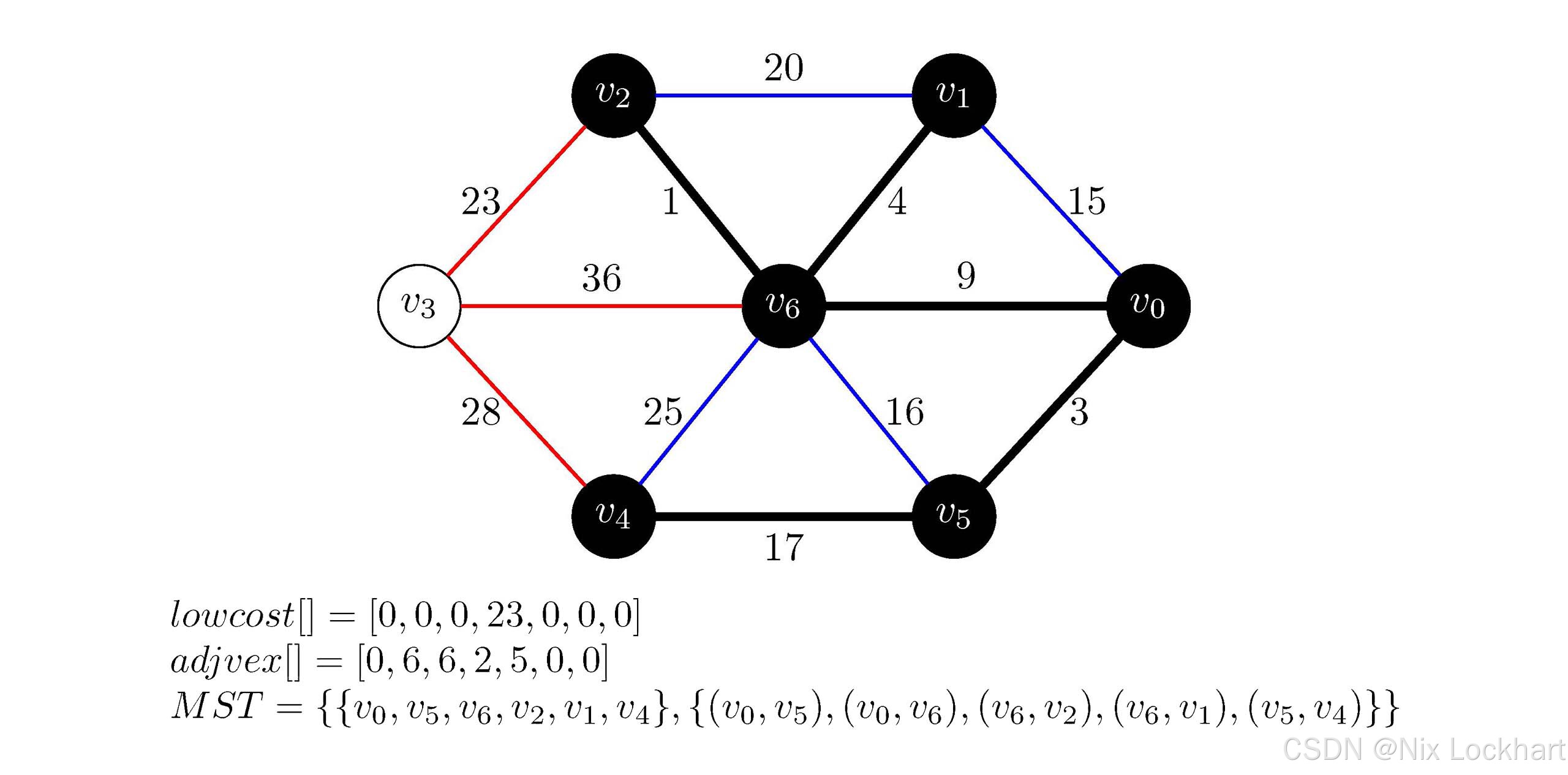
图20:Prim代码执行过程示意6
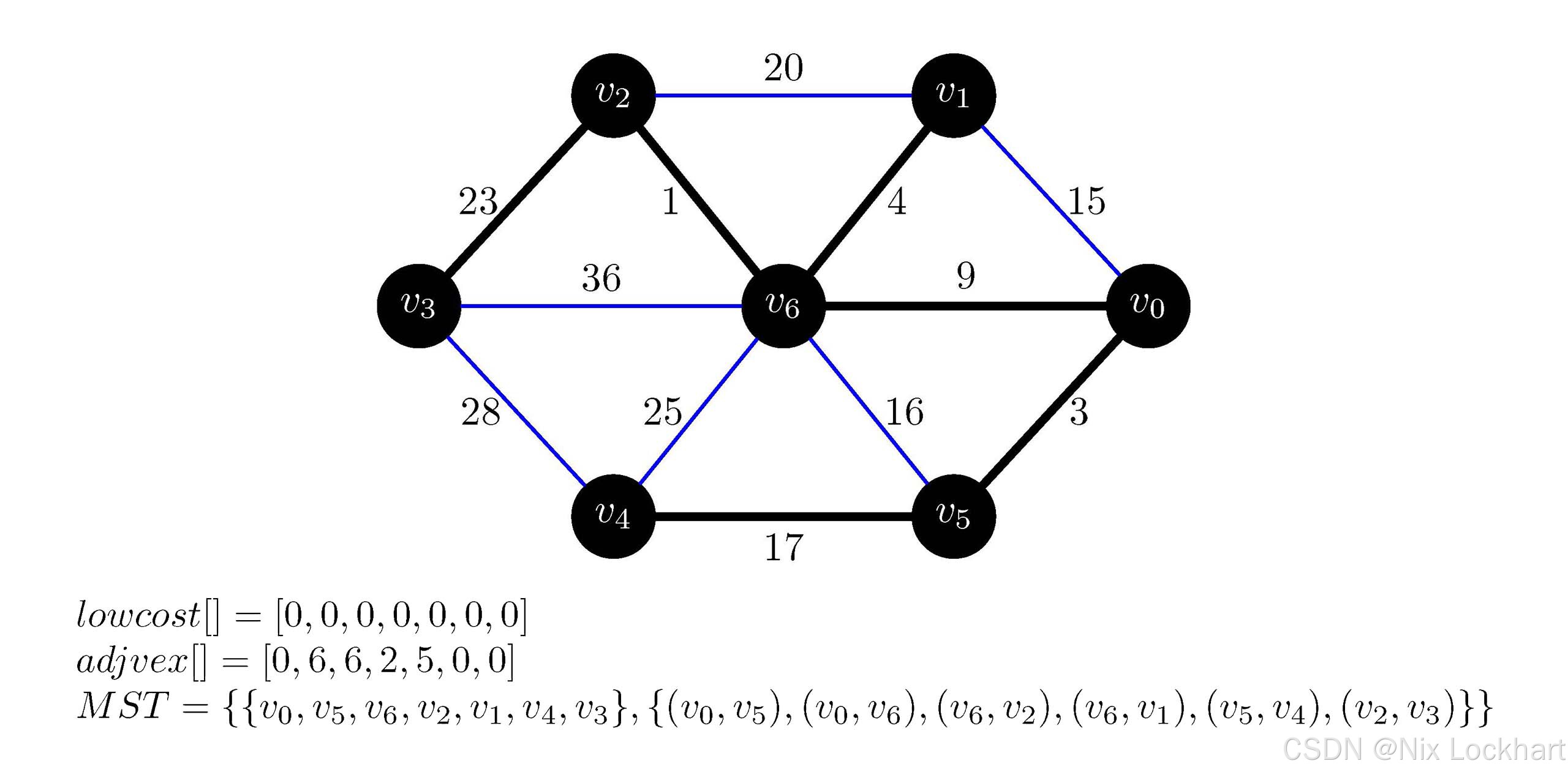
图21:Prim代码执行过程示意7
我们获得了与上面手动分析的结果相同的最小生成树,从而验证了代码的正确性。
但是,我们只是验证了代码实现了我们所提出的Prim算法的核心思想,并不能证明它确实能构造出最小生成树,那么它为什么就能得到最小生成树呢?这就涉及到图论中的一个重要定理------切分定理,通常也会有人称它为最小生成树的性质 或分割性质,它是我们理解和证明Prim算法正确性的关键。
注:下面一部分的内容做拓展性阅读,非必学,若觉得难以理解可直接跳过直接学习Kruskal算法,不影响接下来的学习
2、切分定理(拓展)
切分定理 (Cut Property):设G=(V,E)G=(V,E)G=(V,E)是一个带权连通图,AAA是GGG的某个子集,且AAA包含在GGG的某棵最小生成树中。设SSS是VVV的一个子集,且满足以下条件:
- S≠∅S \neq \varnothingS=∅且S≠VS \neq VS=V。
- 没有任何一条边(u,v)(u,v)(u,v)(u∈S(u \in S(u∈S,v∈V−S)v \in V-S)v∈V−S)属于AAA。
- 边(u,v)(u,v)(u,v)是所有满足u∈Su \in Su∈S且v∈V−Sv \in V-Sv∈V−S的边中权值最小的边。
则边(u,v)(u,v)(u,v)属于某个最小生成树。
其中(S,V−S)(S,V-S)(S,V−S)就是我们口中的"切分",它将顶点集VVV划分为两个不相交的子集SSS和V−SV-SV−S,而如果一条边(u,v)∈E(u,v) \in E(u,v)∈E的两个端点分别位于SSS和V−SV-SV−S中,我们就称这条边横跨这个切分。
其实,用简单话语来描述这个性质就是:将图GGG的顶点集VVV做切分成为SSS和V−SV-SV−S,然后找到所有横跨这个切分的边中权值最小的边(u,v)(u,v)(u,v),那么这条边(u,v)(u,v)(u,v)一定属于某个最小生成树。事实上,这个性质就是我们在前面所学的Prim算法的核心思想,我们上述示意图中的黑色顶点集和白色顶点集就是切分,红色的边就是横跨这个切分的所有边,而我们所做的就是选择这些边中权值最小的边并将其加入到生成树中,蓝色的边则不是横跨这个切分的边,因为它的两个端点都在黑色顶点集中,所以我们在选择边的时候不会考虑它。
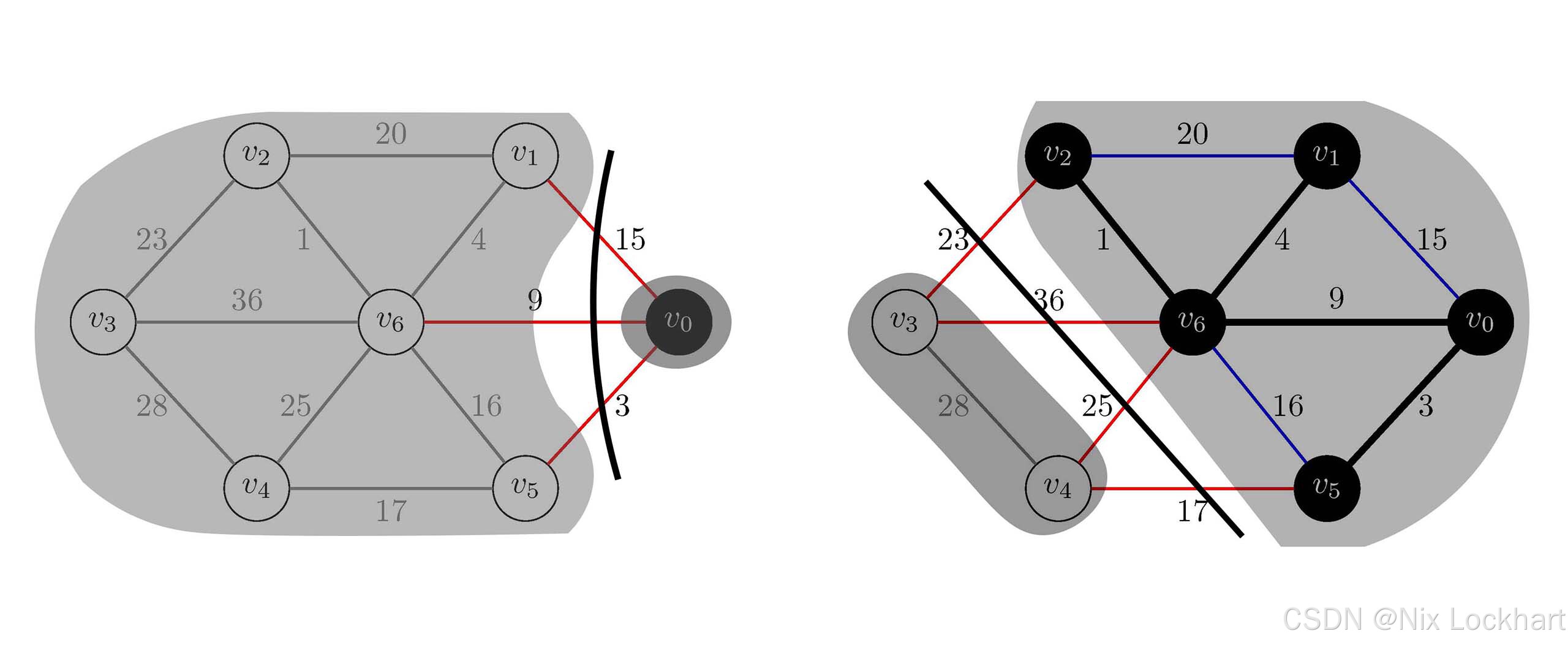
图22:"切分"示意图
但是同样我们还是不知道它的正确性何在,现在我们可以通过反证法来证明这个性质:
注:下面内容中w(u,v)w(u,v)w(u,v)表示边(u,v)(u,v)(u,v)的权值,w(T)w(T)w(T)则表示树TTT的权值
我们先假设边(u,v)(u,v)(u,v)不属于任何最小生成树,那么我们可以找到一棵包含AAA的最小生成树TTT,然后将边(u,v)(u,v)(u,v)加入到TTT中,这样一来就会在TTT中形成一个环,因为TTT已经是一棵生成树了(具体见图的定义中叙述),如下图。
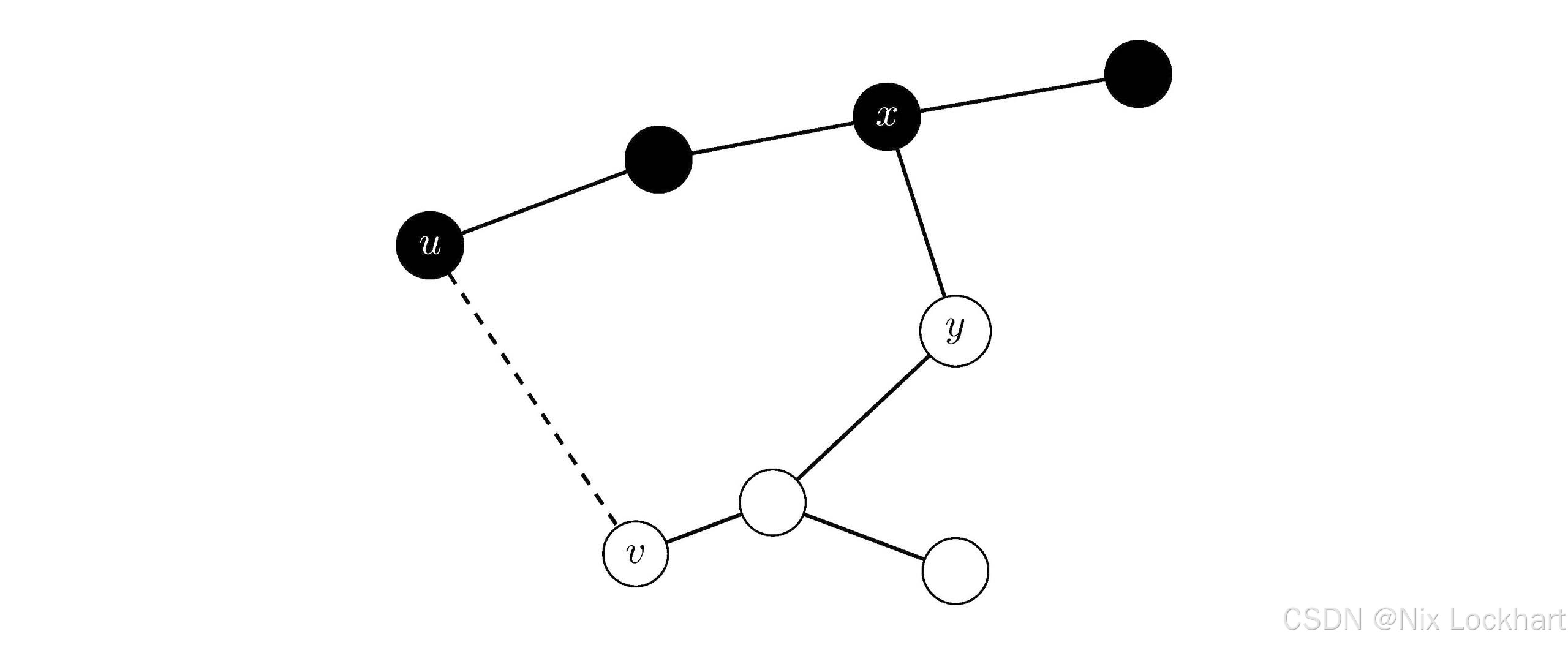
图23:切分定理证明
而加入边(u,v)(u,v)(u,v)之前,树中必然存在一条边(x,y)(x,y)(x,y),它也横跨这个切分(S,V−S)(S,V-S)(S,V−S),否则这个生成树就无法连接起位于SSS和V−SV-SV−S中的顶点了。由于边(u,v)(u,v)(u,v)是所有横跨这个切分的边中权值最小的边,所以有w(u,v)≤w(x,y)w(u,v) \leq w(x,y)w(u,v)≤w(x,y),然后我们将边(x,y)(x,y)(x,y)从TTT中删除,并将边(u,v)(u,v)(u,v)加入到TTT中,这样就得到了另一棵生成树T′T'T′,并且有:
w(T′)=w(T)−w(x,y)+w(u,v)≤w(T)w(T') = w(T) - w(x,y) + w(u,v) \leq w(T)w(T′)=w(T)−w(x,y)+w(u,v)≤w(T)
这就说明我们新找出的生成树T′T'T′的权值不大于原有树TTT的权值,而TTT是一棵最小生成树,所以T′T'T′也一定是一棵最小生成树,并且它包含了边(u,v)(u,v)(u,v),这就与我们所假设的边(u,v)(u,v)(u,v)不属于任何最小生成树矛盾了,所以边(u,v)(u,v)(u,v)一定属于某个最小生成树。
通过上面的证明,我们就可以知道Prim算法为什么能构造出最小生成树了,因为它每次选择的边都是横跨切分的边中权值最小的边,而根据切分定理,这条边一定属于某个最小生成树,所以经过多次迭代后,最终构造出的生成树也一定是最小生成树。
切分定理推论 :设G=(V,E)G=(V,E)G=(V,E)是一个带权连通图,设集合AAA为EEE的某个子集,且AAA包含在图GGG的某个最小生成树中,并设C=(VC,EC)C=(V_C,E_C)C=(VC,EC)为GA=(V,A)G_A=(V,A)GA=(V,A)中的某个连通分量。若边(u,v)(u,v)(u,v)是连接CCC与GAG_AGA中某个其他连通分量的所有边中权值最小的边,则边(u,v)(u,v)(u,v)属于某个最小生成树。
若是上面看的云里雾里,我们用更通俗的话来讲:假设我们有一个带权连通图,并且已经选好了一些边(集合AAA),这些边都是某个最小生成树的一部分。由于这些边可能还不足以连接所有顶点,所以它们形成了若干个不相连的"孤岛"(连通分量)。而现在,如果我们选取其中一个孤岛CCC,并找到一条连接这个孤岛与其他孤岛之间权值最小的边(u,v)(u,v)(u,v),那么这条边一定也是某个最小生成树的一部分。
这个推论其实就是切分定理的一个特例,我们可以将孤岛CCC作为切分中的一个子集SSS,而因为它作为一个孤岛,必然与V−SV-SV−S中其余孤岛是没有边的,那我们就可以将其他孤岛的顶点集作为另一个子集V−SV-SV−S,这样就满足了切分定理中的所有条件,所以这个推论也是成立的。
我们将上述Prim算法找出的最小生成树拆分为三个"孤岛"
C1={{v0,v5,v4},{(v0,v5),(v5,v4)}}C_1 = \{\{v_0,v_5,v_4\},\{(v_0,v_5),(v_5,v_4)\}\}C1={{v0,v5,v4},{(v0,v5),(v5,v4)}} C2={{v1}}C_2 = \{\{v_1\}\}C2={{v1}} C3={{v6,v2,v3},{(v6,v2),(v2,v3)}}C_3 = \{\{v_6,v_2,v_3\},\{(v_6,v_2),(v_2,v_3)\}\}C3={{v6,v2,v3},{(v6,v2),(v2,v3)}}
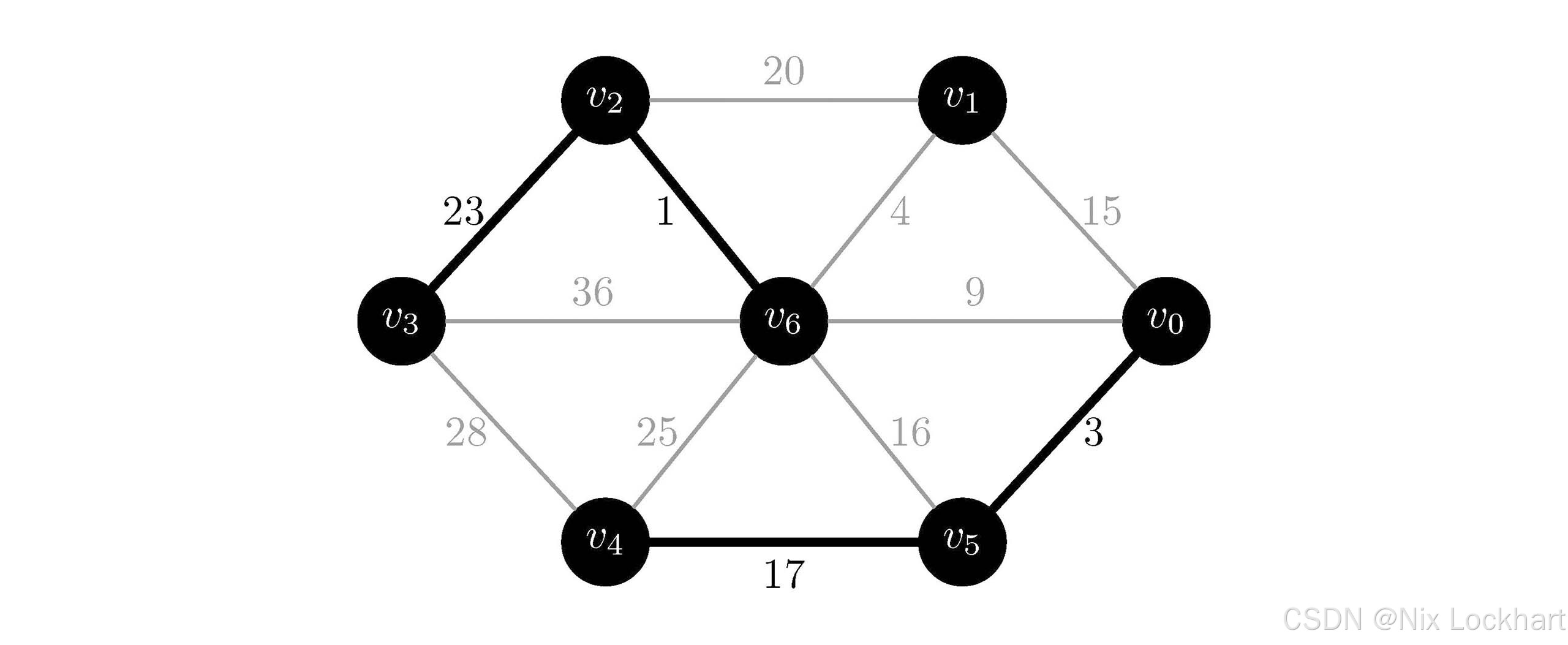
图24:Prim算法结果拆分为孤岛
然后我们看孤岛C1C_1C1,找出连接它与其他孤岛之间权值最小的边,它是边(v0,v6)(v_0,v_6)(v0,v6),根据推论,这条边一定属于某个最小生成树;同理,我们看孤岛C2C_2C2,找出连接它与其他孤岛之间权值最小的边,它是边(v1,v6)(v_1,v_6)(v1,v6)。将这两条边加入到集合AAA中,我们就又重新得到了我们使用Prim算法所构造出的最小生成树。
不难发现,我们的"孤岛"可以是单个顶点,那这样一来,我们是不是可以将每个顶点都看作一个孤岛呢?这样的话,我们就可以将重点放在边的选择上,即:每次选择连接两个孤岛之间权值最小的边,并将其加入到生成树中,直到所有顶点都被连接起来为止。而这,正是最小生成树的另一种经典构造策略------Kruskal算法。
3、克鲁斯卡尔(Kruskal)算法
从上一部分分析中可以看出,Kruskal算法是站在上帝视角的,对于边的考虑是全局的,而不是像Prim算法那样从某个顶点出发,逐步扩展生成树。Kruskal算法的核心思想是:将图中的所有边按权值从小到大排序,然后依次选择这些边,若选择的边连接的两个顶点属于不同的连通分量(即不在同一个孤岛中),则将这条边加入到生成树中,并将这两个连通分量合并为一个连通分量;否则,若选择的边连接的两个顶点已经在同一个连通分量中(即在同一个孤岛中),则跳过这条边。重复上述过程,直到生成树中包含了图中的所有顶点为止。
我们还是使用之前的带权图来演示Kruskal算法的过程:
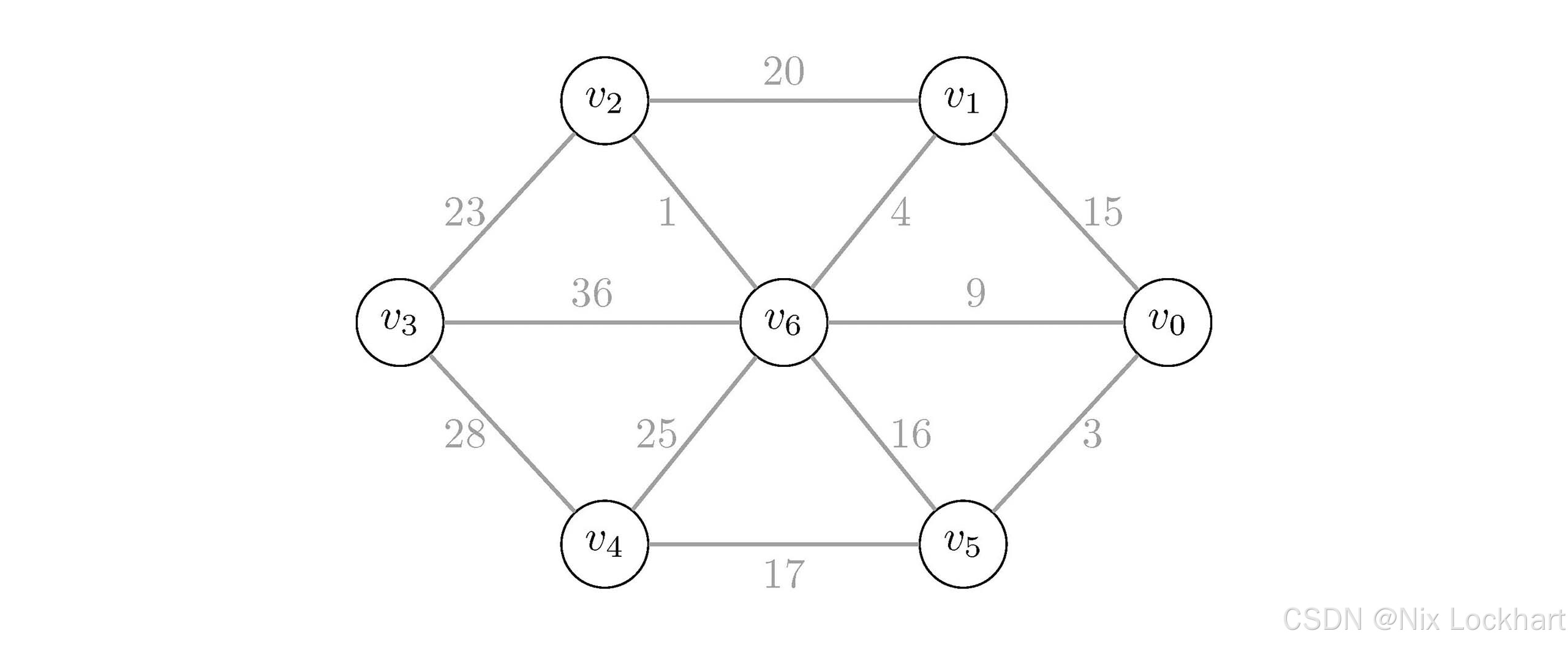
图25:一个带权图
首先我们将图中的所有边按权值从小到大排序,得到下表:
| 边 | (v2,v6)(v_2,v_6)(v2,v6) | (v0,v5)(v_0,v_5)(v0,v5) | (v1,v6)(v_1,v_6)(v1,v6) | (v0,v6)(v_0,v_6)(v0,v6) | (v0,v1)(v_0,v_1)(v0,v1) | (v5,v6)(v_5,v_6)(v5,v6) | (v4,v5)(v_4,v_5)(v4,v5) | (v1,v2)(v_1,v_2)(v1,v2) | (v2,v3)(v_2,v_3)(v2,v3) | (v4,v6)(v_4,v_6)(v4,v6) | (v3,v4)(v_3,v_4)(v3,v4) | (v3,v6)(v_3,v_6)(v3,v6) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 权值 | 1 | 3 | 4 | 9 | 15 | 16 | 17 | 20 | 23 | 25 | 28 | 36 |
然后我们依次选择这些边,首先选择权值最小的边(v2,v6)(v_2,v_6)(v2,v6),因为此时所有顶点都还没有被连接,所以它们肯定属于不同的连通分量,我们将这条边加入到生成树中,并将顶点v2v_2v2和v6v_6v6合并为一个连通分量,即它们俩组成了一个"孤岛",如下:
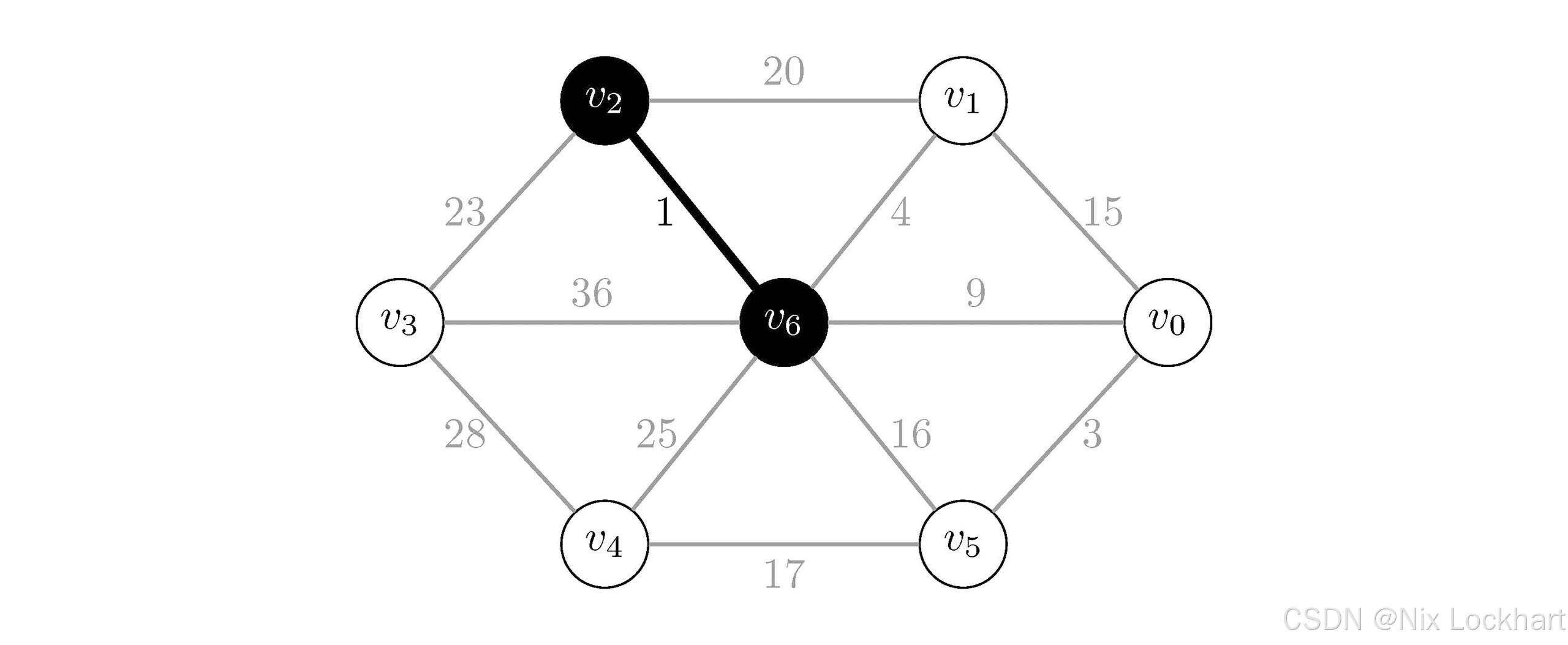
图26:Kruskal算法过程1
接下来选择权值为3的边(v0,v5)(v_0,v_5)(v0,v5),同理,它们也属于不同的连通分量,我们将这条边加入到生成树中,并将顶点v0v_0v0所在的连通分量和v5v_5v5所在的连通分量合并为一个连通分量,如下:
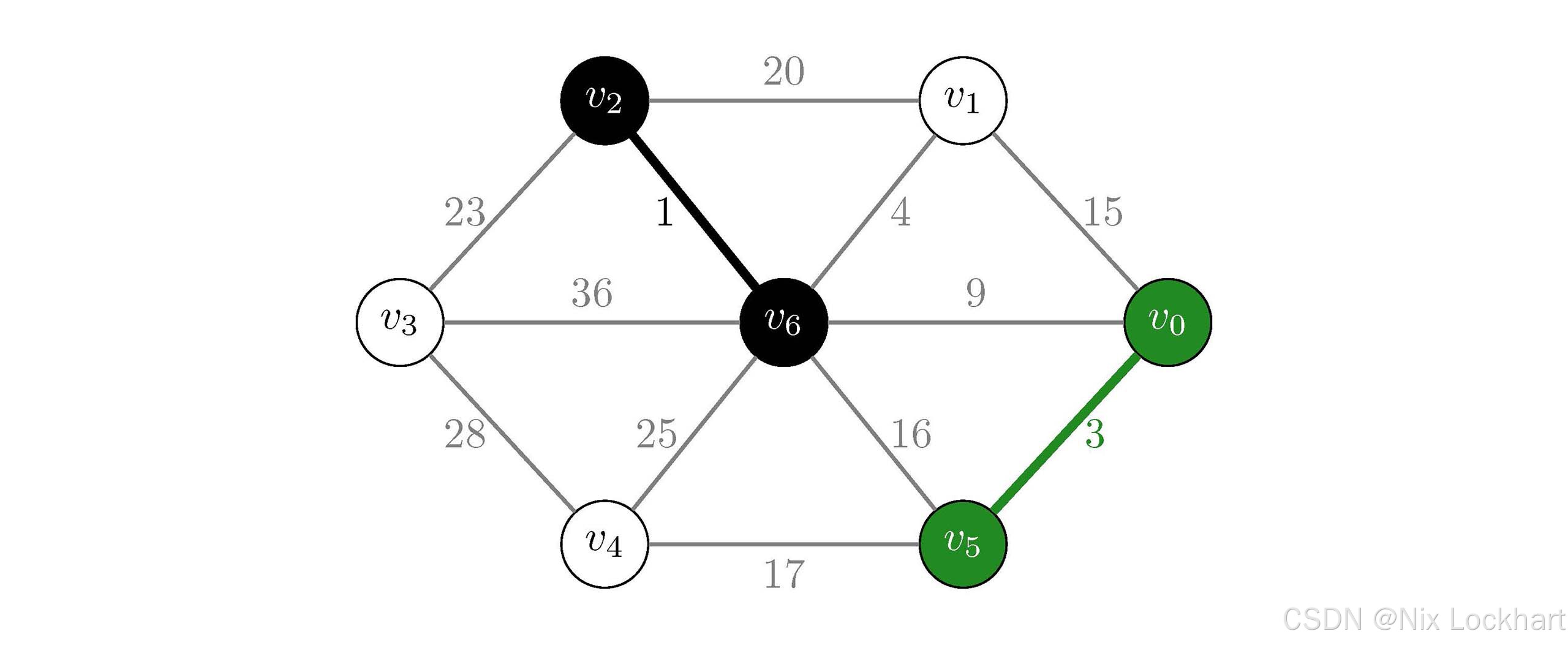
图27:Kruskal算法过程2
然后选择权值为4的边(v1,v6)(v_1,v_6)(v1,v6),顶点v1v_1v1和v6v_6v6属于不同的连通分量,我们将这条边加入到生成树中,并将顶点v1v_1v1所在的连通分量和v6v_6v6所在的连通分量合并为一个连通分量,如下:
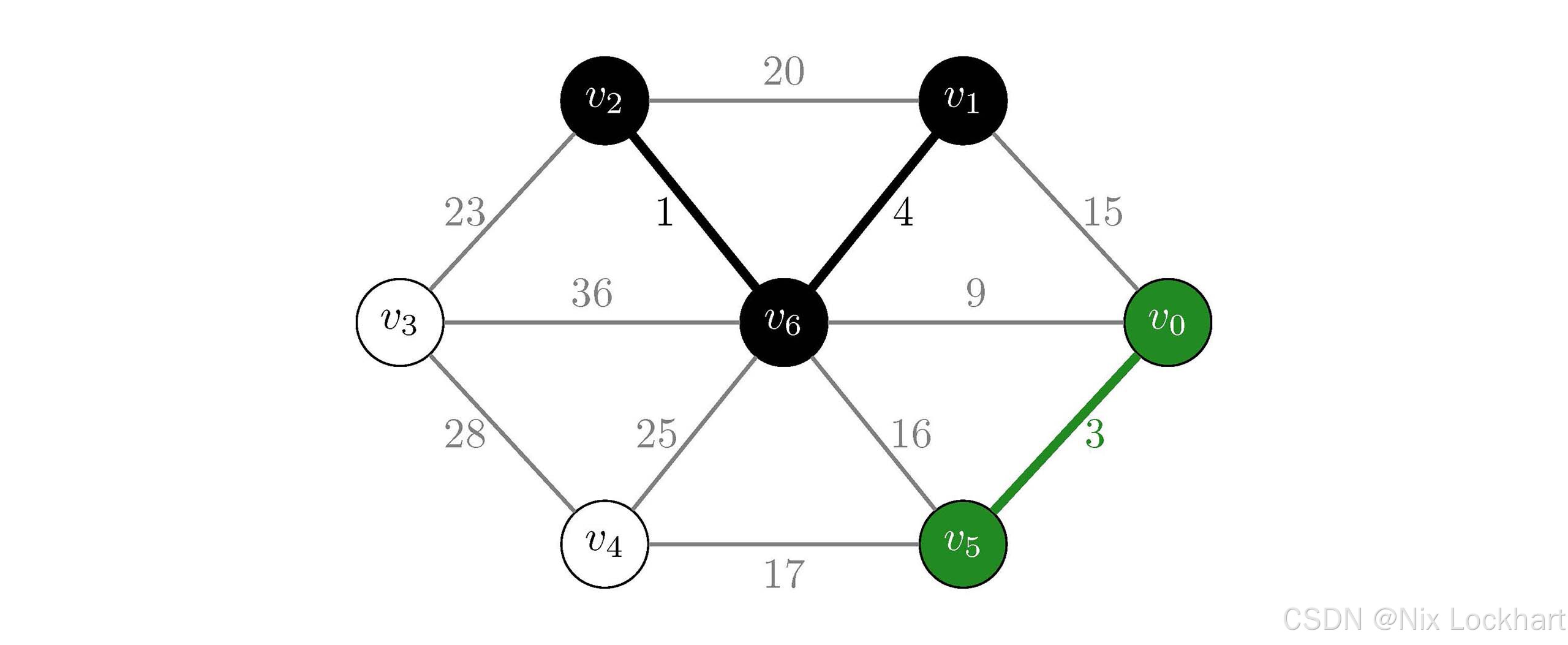
图28:Kruskal算法过程3
接下来选择权值为9的边(v0,v6)(v_0,v_6)(v0,v6),顶点v0v_0v0和v6v_6v6属于我们刚找出的两个连通分量,所以我们同样将这条边加入到生成树中,并将顶点v0v_0v0所在的连通分量和v6v_6v6所在的连通分量合并为一个大的连通分量,如下:
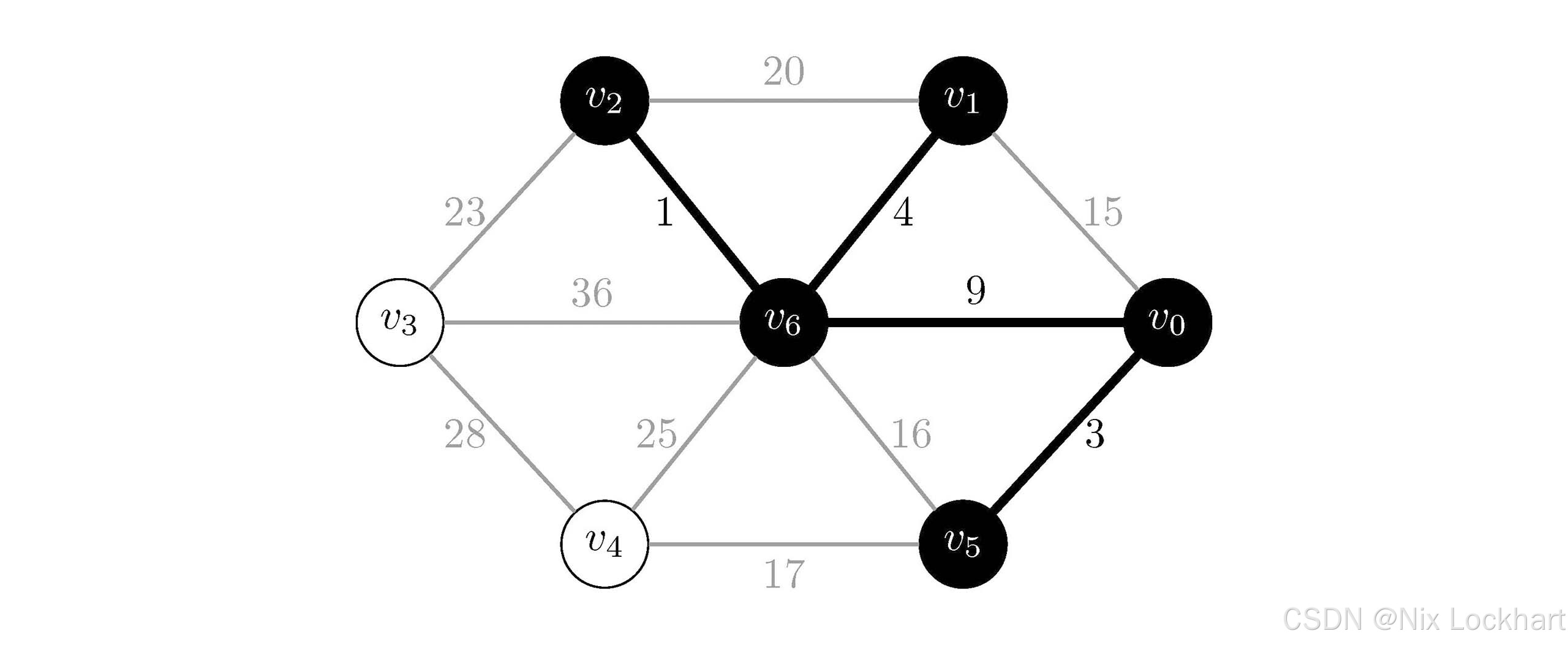
图29:Kruskal算法过程4
然后选择权值为15的边(v0,v1)(v_0,v_1)(v0,v1),顶点v0v_0v0和v1v_1v1已经在我们刚合并出的大连通分量中了,所以我们跳过这条边,继续选择权值为16的边(v5,v6)(v_5,v_6)(v5,v6),顶点v5v_5v5和v6v_6v6也已经在同一个连通分量中了,所以我们也跳过这条边,继续选择权值为17的边(v4,v5)(v_4,v_5)(v4,v5),顶点v4v_4v4和v5v_5v5属于不同的连通分量,我们将这条边加入到生成树中,并将顶点v4v_4v4所在的连通分量和v5v_5v5所在的连通分量合并为一个大的连通分量,如下:
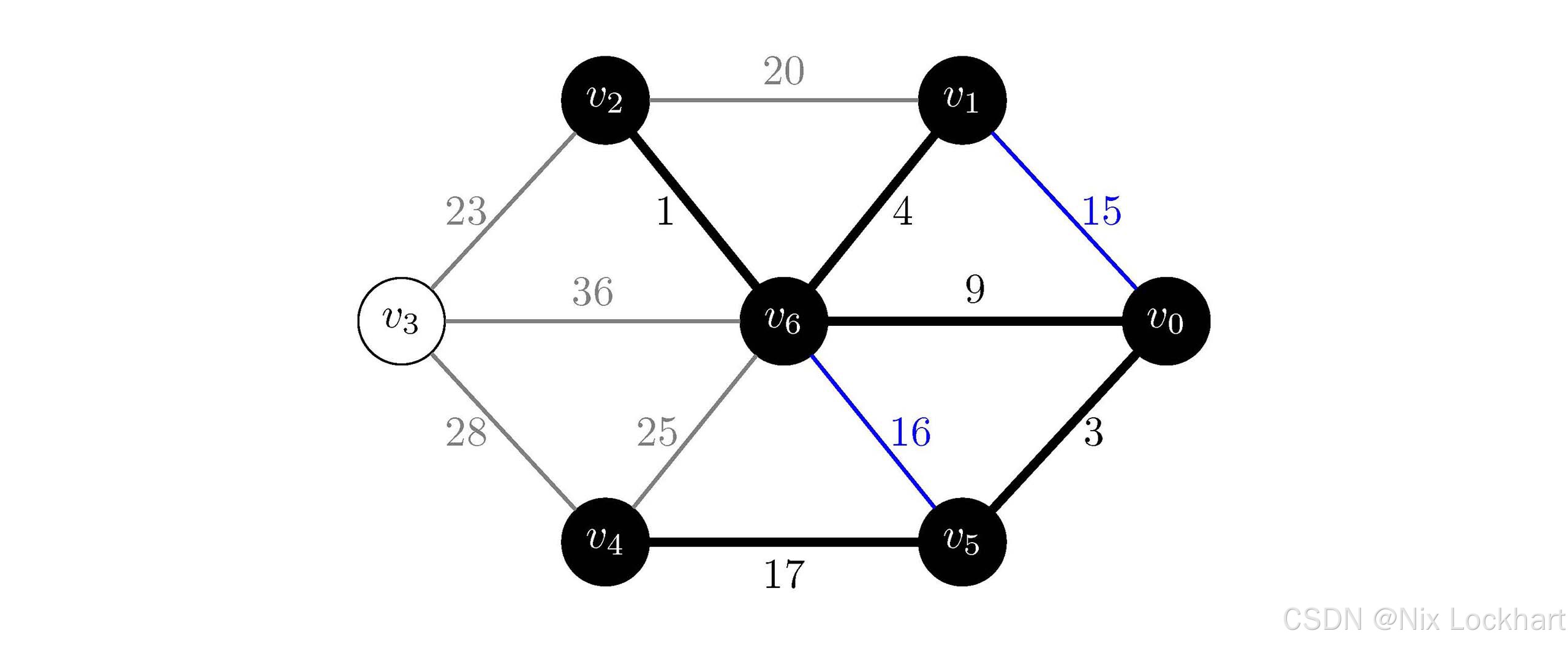
图30:Kruskal算法过程5
接下来选择权值为20的边(v1,v2)(v_1,v_2)(v1,v2),顶点v1v_1v1和v2v_2v2在同一连通分量中,跳过,继续选择权值为23的边(v2,v3)(v_2,v_3)(v2,v3),顶点v2v_2v2和v3v_3v3属于不同的连通分量,我们将这条边加入到生成树中,并将顶点v2v_2v2所在的连通分量和v3v_3v3所在的连通分量合并为一个连通分量,如下:
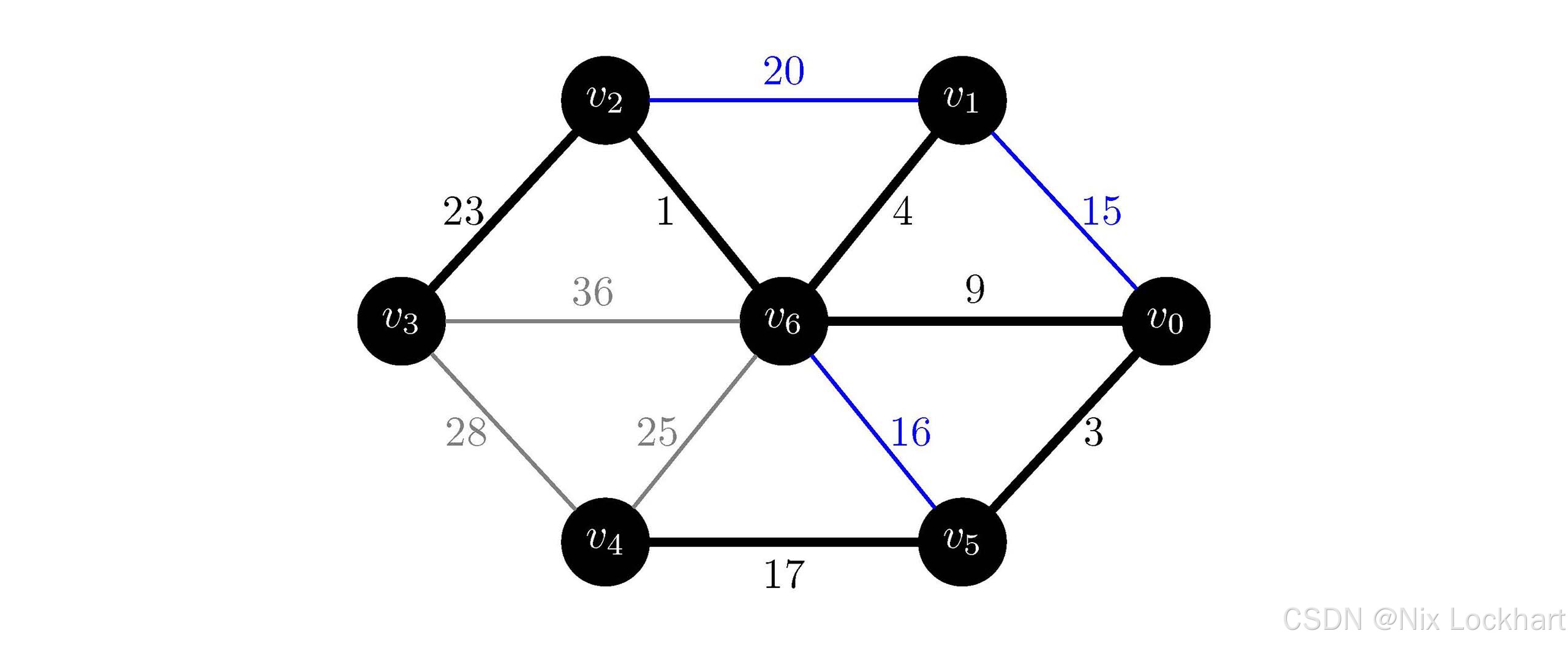
图31:Kruskal算法过程6
此时我们的生成树中已经包含了图中的所有顶点和连接它们所需的最少边,算法结束。我们看出来,最终我们得到的最小生成树与之前使用Prim算法得到的结果是完全相同的,同时也说明了Kruskal算法的正确性。
接下来我们给出Kruskal算法的邻接矩阵存储结构实现代码:
c
#define MAXVEX 100 // 最大顶点数
#define INFINITY 65535 // 用于表示无穷大
typedef struct
{
int begin; // 边的起点
int end; // 边的终点
int weight; // 边的权值
} Edge;
int Find(int parent[], int f) // 查找顶点f的终点
{
while (parent[f] >= 0)
f = parent[f];
return f;
}
c
void Kruskal(GraphAdjMatrix G)
{
int i, j, k;
int parent[MAXVEX]; // 用于保存每个顶点的终点
Edge edges[MAXVEX]; // 用于保存图中的所有边
// 将图中的所有边信息存入edges数组中并按权值从小到大排序edges数组
ConvertAndSort(G, edges);
// 初始化parent数组
for (i = 0; i < G.numVertexes; i++)
parent[i] = -1; // -1表示该顶点还没有终点
// 构造最小生成树
for (i = 0; i < G.numEdges; i++)
{
j = Find(parent, edges[i].begin); // 查找边的起点的终点
k = Find(parent, edges[i].end); // 查找边的终点的终点
if (j != k) // 如果两个顶点不在同一个连通分量中
{
parent[j] = k; // 将两个连通分量合并
printf("(%c, %c) ", G.vexs[edges[i].begin], G.vexs[edges[i].end]); // 输出边
}
}
}其中多出了一个结构体Edge,用于保存边的信息,包括边的起点、终点和权值,方便我们对其进行排序;以及两个辅助函数ConvertAndSort()和Find,前者用于将图中的所有边信息存入edges数组中并按权值从小到大排序,很好理解,后者用于查找顶点的终点,什么叫顶点的终点呢?我们可以将每个连通分量看作一棵树(因为它就是我们最终找出的最小生成树的一部分),而树的根节点就是这个连通分量的终点,所以我们通过Find函数用于找到某个顶点所在连通分量的根节点,从而判断两个顶点是否在同一个连通分量中。
我们来具体分析一下调用Kruskal(G)的代码执行过程:
- 1~8行不用再说,就是我们上面所提到的准备工作,将图中的所有边信息存入
edges数组中并按权值从小到大排序得到我们上述的表格。 - 10~12行初始化
parent数组,parent[i]表示顶点viv_ivi的终点,若parent[i]为-1,则表示顶点viv_ivi还没有终点。 - 14~24行的
for循环就是Kruskal算法的核心思想了,循环变量i从0开始,依次选择排序后的边。 - 第16~17行,调用
Find函数查找边的起点和终点的终点,若它们不相同,则表示这两个顶点不在同一个连通分量中:
如我们一开始是j=Find(parent, 2)和k=Find(parent, 6),由于顶点v2v_2v2和v6v_6v6已经是它们所在的树的根了parent[2,6]=-1,所以返回的就是2和6,它们并不相同,所以我们将这条边加入到生成树中。并在第21行将两个连通分量合并parent[2]=6,我们在图示中用红色来标识每个连通分量的终点(树的根),即将起点的终点指向终点的终点(这里我们是将j指向k,也可以反过来),表示将顶点v2v_2v2所在的连通分量和v6v_6v6所在的连通分量合并为一个连通分量。
此时我们得到:
parent[]=[−1,−1,6,−1,−1,−1,−1]parent[]=[-1,-1,6,-1, -1, -1, -1]parent[]=[−1,−1,6,−1,−1,−1,−1] MST={{v2,v6},{(v2,v6)}}MST=\{\{v_2,v_6\},\{(v_2,v_6)\}\}MST={{v2,v6},{(v2,v6)}}
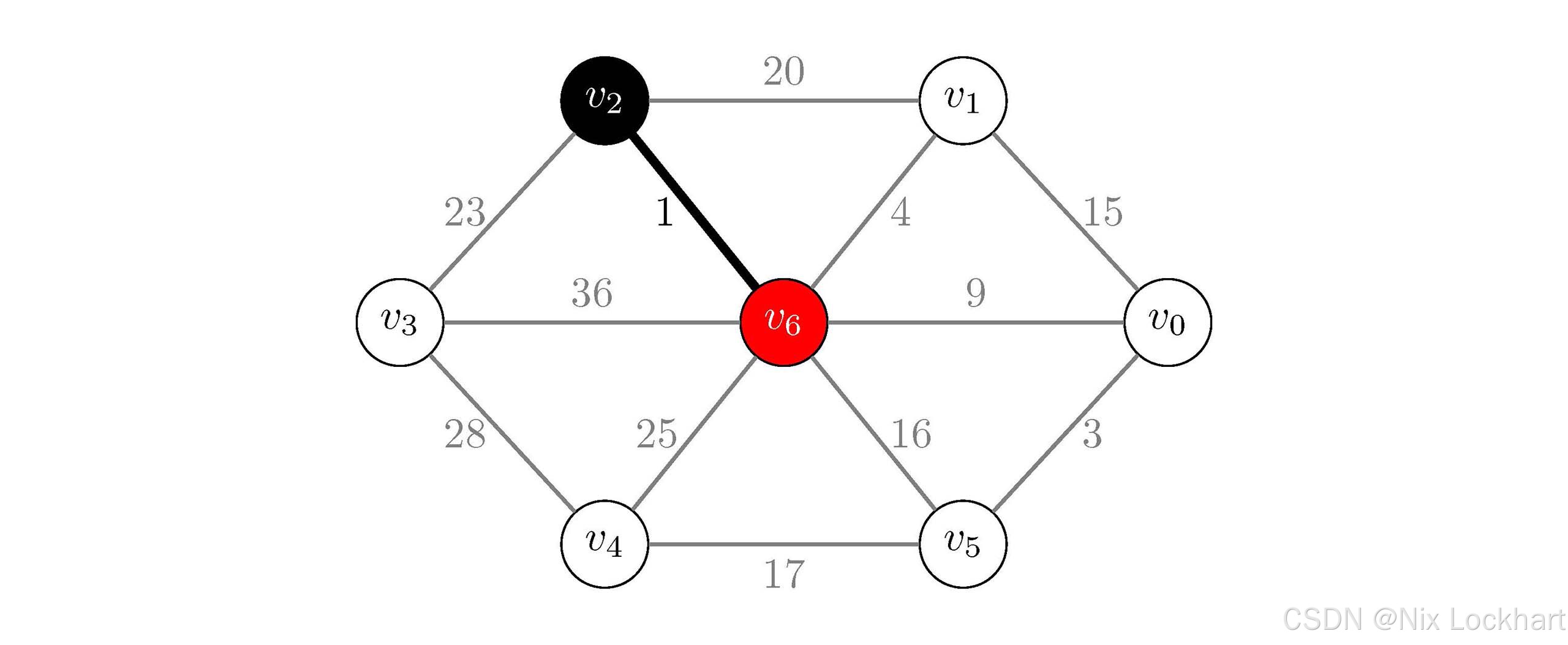
图32:Kruskal代码分析过程示意1
接下来i=1时,j=Find(parent, 0)=0和k=Find(parent, 5)=5,同理,它们并不相同,所以我们将这条边加入到生成树中,并将顶点v0v_0v0所在的连通分量和v5v_5v5所在的连通分量合并为一个连通分量,即parent[0]=5。
此时我们得到:
parent[]=[5,−1,6,−1,−1,−1,−1]parent[]=[5,-1,6,-1, -1, -1, -1]parent[]=[5,−1,6,−1,−1,−1,−1] MST={{v0,v5,v2,v6},{(v2,v6),(v0,v5)}}MST=\{\{v_0,v_5,v_2,v_6\},\{(v_2,v_6),(v_0,v_5)\}\}MST={{v0,v5,v2,v6},{(v2,v6),(v0,v5)}}
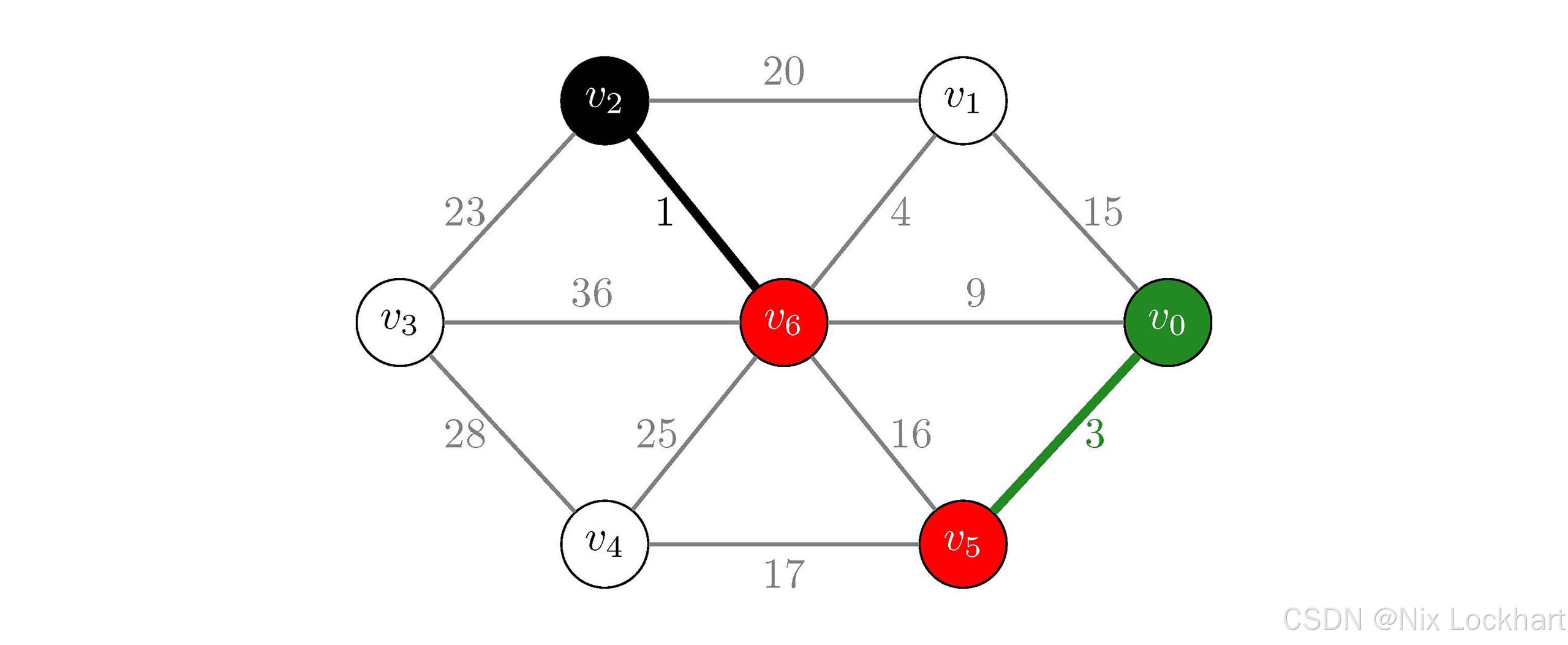
图33:Kruskal代码分析过程示意2
接下来i=2,j=Find(parent, 1)=1和k=Find(parent, 6)=6,它们并不相同,所以我们将这条边加入到生成树中,并将顶点v1v_1v1所在的连通分量和v6v_6v6所在的连通分量合并为一个连通分量,即parent[1]=6。
此时我们有:
parent[]=[5,6,6,−1,−1,−1,−1]parent[]=[5,6,6,-1, -1, -1, -1]parent[]=[5,6,6,−1,−1,−1,−1] MST={{v0,v5,v1,v2,v6},{(v2,v6),(v0,v5),(v1,v6)}}MST=\{\{v_0,v_5,v_1,v_2,v_6\},\{(v_2,v_6),(v_0,v_5),(v_1,v_6)\}\}MST={{v0,v5,v1,v2,v6},{(v2,v6),(v0,v5),(v1,v6)}}
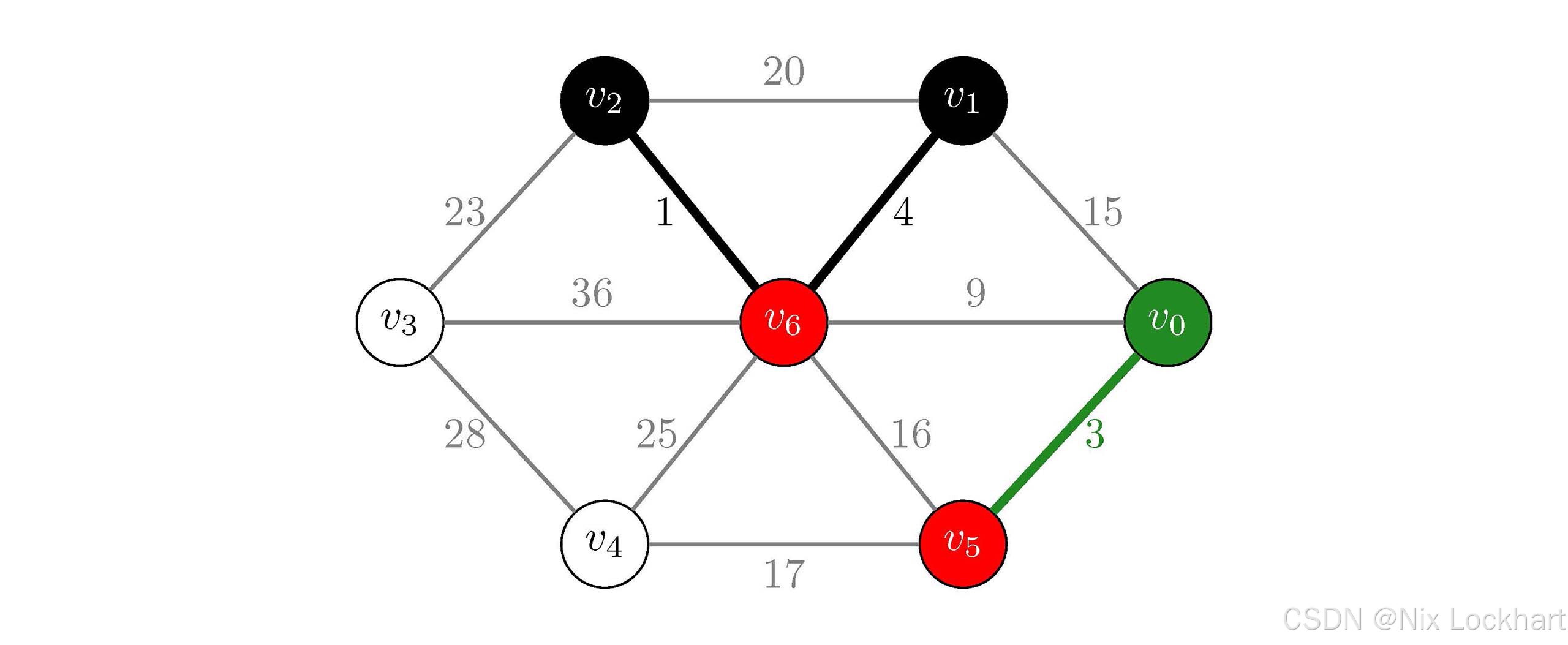
图34:Kruskal代码分析过程示意3
然后i=3,j=Find(parent, 0)=5和k=Find(parent, 6)=6,它们也不相同,所以我们将这条边加入到生成树中,并将顶点v0v_0v0所在的连通分量和v6v_6v6所在的连通分量合并为一个连通分量,即parent[5]=6。
此时:
parent[]=[5,6,6,−1,−1,6,−1]parent[]=[5,6,6,-1, -1, 6, -1]parent[]=[5,6,6,−1,−1,6,−1] MST={{v0,v5,v1,v2,v6},{(v2,v6),(v0,v5),(v1,v6),(v0,v6)}}MST=\{\{v_0,v_5,v_1,v_2,v_6\},\{(v_2,v_6),(v_0,v_5),(v_1,v_6),(v_0,v_6)\}\}MST={{v0,v5,v1,v2,v6},{(v2,v6),(v0,v5),(v1,v6),(v0,v6)}}
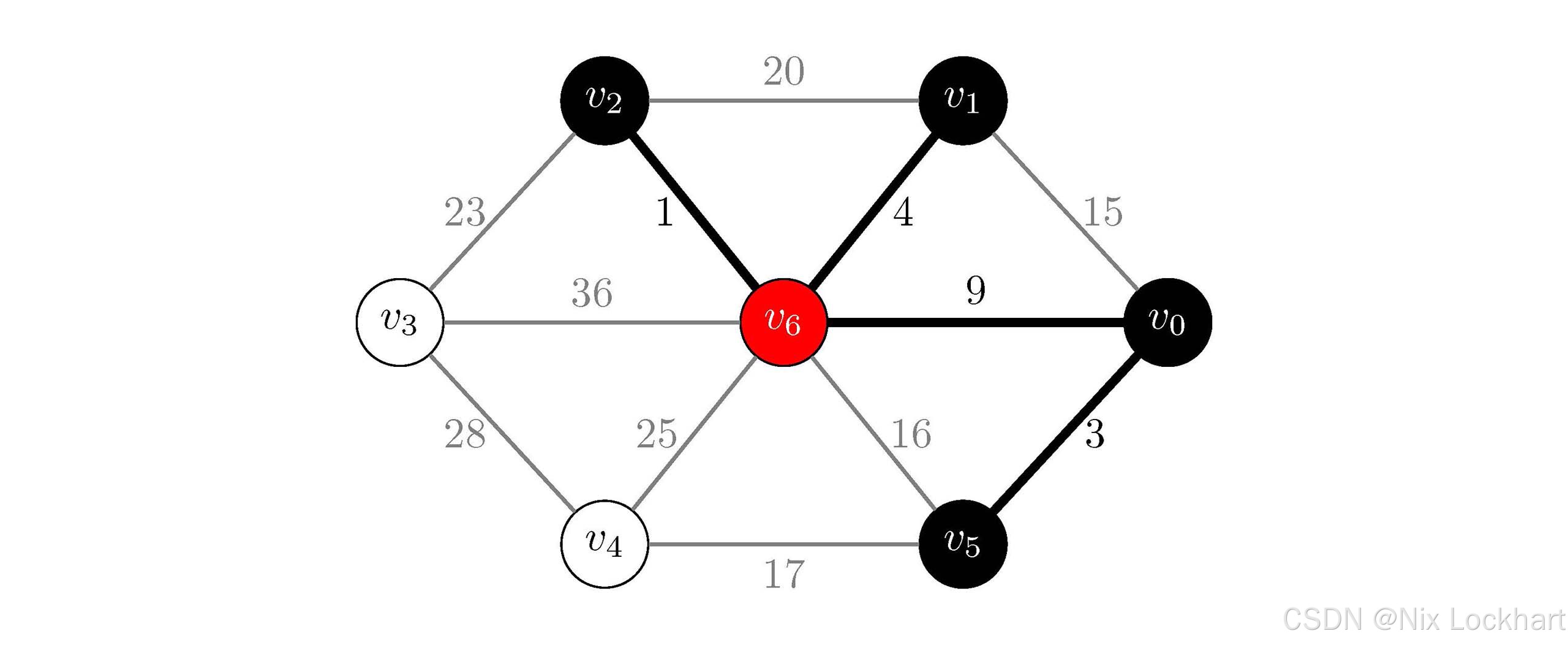
图35:Kruskal代码分析过程示意4
接下来i=4,j=Find(parent, 0)=6和k=Find(parent, 1)=6,它们的结果相同,说明顶点v0v_0v0和v1v_1v1已经在同一个连通分量中,所以我们跳过这条边。继续i=5,j=Find(parent, 5)=6和k=Find(parent, 6)=6,它们也相同,所以我们也跳过这条边,继续i=6,j=Find(parent, 4)=4和k=Find(parent, 5)=6,它们并不相同,所以我们将这条边加入到生成树中,并将顶点v4v_4v4所在的连通分量和v5v_5v5所在的连通分量合并为一个连通分量,即parent[4]=6。
此时:
parent[]=[5,6,6,−1,6,6,−1]parent[]=[5,6,6,-1, 6, 6, -1]parent[]=[5,6,6,−1,6,6,−1] MST={{v0,v5,v1,v2,v4,v6},{(v2,v6),(v0,v5),(v1,v6),(v0,v6),(v4,v5)}}MST=\{\{v_0,v_5,v_1,v_2,v_4,v_6\},\{(v_2,v_6),(v_0,v_5),(v_1,v_6),(v_0,v_6),(v_4,v_5)\}\}MST={{v0,v5,v1,v2,v4,v6},{(v2,v6),(v0,v5),(v1,v6),(v0,v6),(v4,v5)}}
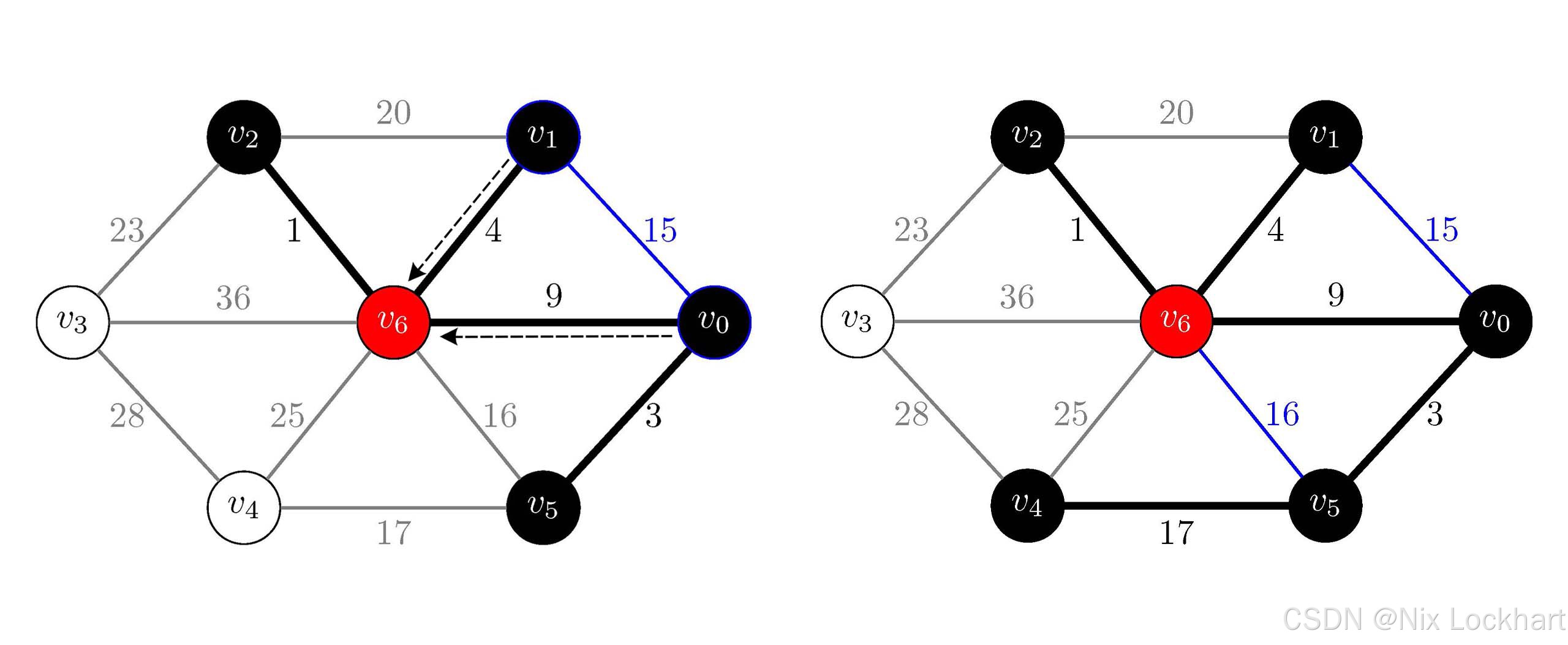
图36:Kruskal代码分析过程示意5
接下来i=7,j=Find(parent, 1)和k=Find(parent, 2),它们结果也相同,跳过。i=8,j=Find(parent, 2)和k=Find(parent, 3),它们结果不相同,所以我们将这条边加入到生成树中,并将顶点v2v_2v2所在的连通分量和v3v_3v3所在的连通分量合并为一个连通分量,即parent[3]=6。
此时:
parent[]=[5,6,6,6,6,6,−1]parent[]=[5,6,6,6, 6, 6, -1]parent[]=[5,6,6,6,6,6,−1] MST={{v0,v5,v1,v2,v3,v4,v6},{(v2,v6),(v0,v5),(v1,v6),(v0,v6),(v4,v5),(v2,v3)}}MST=\{\{v_0,v_5,v_1,v_2,v_3,v_4,v_6\},\{(v_2,v_6),(v_0,v_5),(v_1,v_6),(v_0,v_6),(v_4,v_5),(v_2,v_3)\}\}MST={{v0,v5,v1,v2,v3,v4,v6},{(v2,v6),(v0,v5),(v1,v6),(v0,v6),(v4,v5),(v2,v3)}}
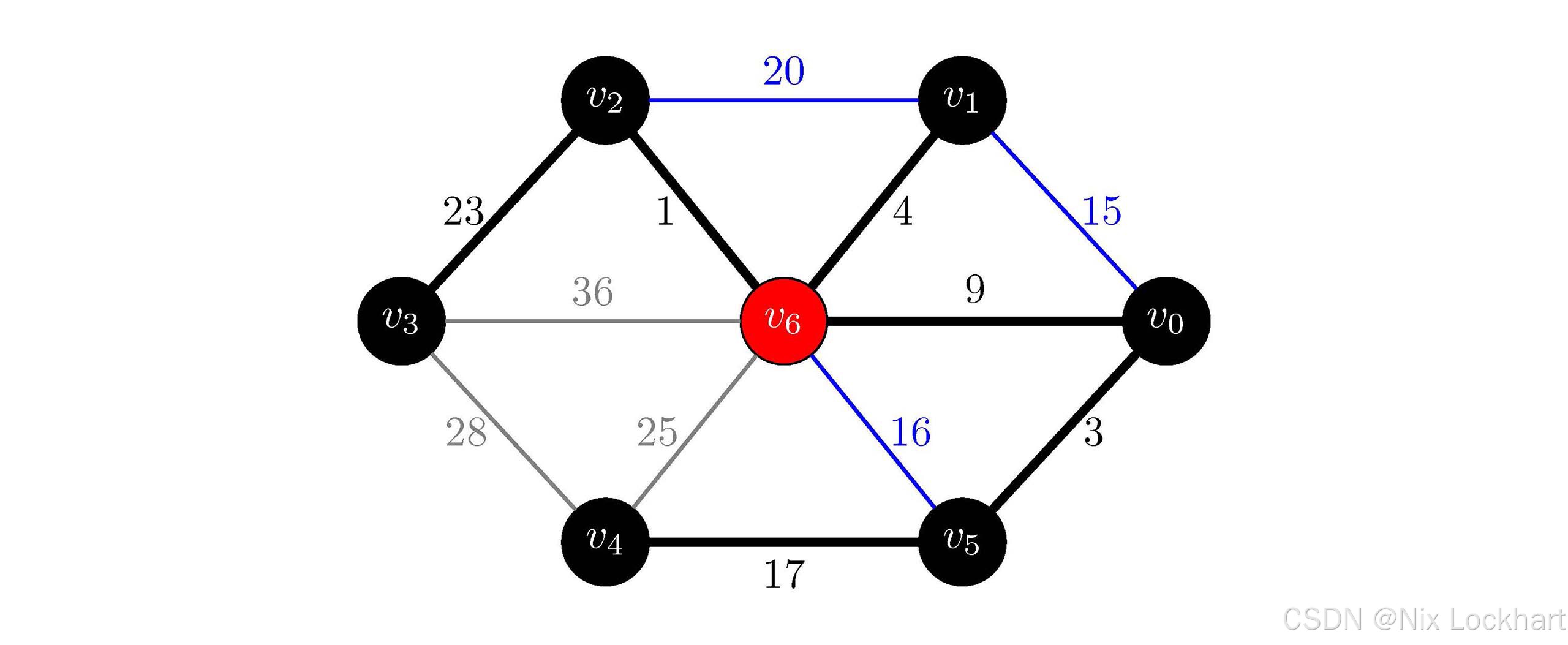
图37:Kruskal代码分析过程示意6
此时在我们进行过程探索时,生成树中已经包含了图中的所有顶点,我们说算法结束,但是大家还是需要知道,代码中并没有判断生成树是否包含了所有顶点,而是继续执行i=9,10,11,发现它们的结果都是相同的,所以都跳过了,然后才是算法结束。
4、小结
本节我们学习了两种经典的最小生成树算法------Prim算法和Kruskal算法,并通过代码实现加深了对它们的理解,同时也学习了切分定理,这个定理是我们理解和证明构造最小生成树算法正确性的关键。
需要注意的是,Prim算法和Kruskal算法虽然都能构造出最小生成树,但它们的适用场景有所不同。我们来分析一下Prim算法的时间复杂度,我们分析代码知道,Prim算法的时间复杂度主要取决于两个部分:
- 初始化
lowcost和adjvex数组的时间复杂度为O(V)O(V)O(V),其中VVV为图中的顶点数。 - 构造最小生成树的时间复杂度为O(V2)O(V^2)O(V2),因为外层循环执行V−1V-1V−1次,而内层循环执行VVV次。
我们知道,O(V2)O(V^2)O(V2)占据了主导地位,所以Prim算法的时间复杂度为O(V2)O(V^2)O(V2),适用于顶点数较少而边数较多的稠密图。
接下来我们分析一下Kruskal算法的时间复杂度,Kruskal算法的时间复杂度主要取决于两个部分:
- 将图中的所有边信息存入
edges数组中并按权值从小到大排序的时间复杂度为O(ElogE)O(E \log E)O(ElogE),其中EEE为图中的边数,因为一般排序算法的时间复杂度为O(nlogn)O(n \log n)O(nlogn)。 - 构造最小生成树的时间复杂度为O(ElogV)O(E \log V)O(ElogV),因为循环执行EEE次,而每次调用
Find函数的时间复杂度为O(logV)O(\log V)O(logV),这是因为Find()函数中有一个while循环,而每次循环都将f更新为parent[f],而parent[f]指向的是树的根节点,所以循环的次数不会超过树的高度,而一棵有VVV个节点的树的高度不会超过logV\log VlogV。
则Kruskal时间复杂度为O(ElogE+ElogV)O(E \log E + E \log V)O(ElogE+ElogV),由于EEE最大为V(V−1)/2V(V-1)/2V(V−1)/2,所以logE\log ElogE的数量级与logV\log VlogV是相同的,所以Kruskal算法的时间复杂度可以简化为O(ElogV)O(E \log V)O(ElogV)(或者也可以直接记为O(ElogE)O(E \log E)O(ElogE)),适用于边数较少而顶点数较多的稀疏图。
于是我们就可以给出下表,总结Prim算法和Kruskal算法的异同:
| 算法 | 核心思想 | 时间复杂度 | 适用场景 |
|---|---|---|---|
| Prim算法 | 从某个顶点出发,逐步扩展生成树 | O(V2)O(V^2)O(V2) | 顶点数较少而边数较多的稠密图 |
| Kruskal算法 | 将所有边按权值排序,依次选择边并连接不同连通分量 | O(ElogV)O(E \log V)O(ElogV) | 边数较少而顶点数较多的稀疏图 |