
- 使用8维状态模型,全面描述了平面运动中的位置、速度、姿态和传感器偏差,采用容积卡尔曼滤波器处理非线性问题,相比传统EKF具有更好的数值稳定性和精度,实现了IMU与GNSS的有效融合,充分发挥两种传感器的互补优势
文章目录
程序简介
核心创新:
- 使用8维状态模型,全面描述了平面运动中的位置、速度、姿态和传感器偏差
- 采用容积卡尔曼滤波器处理非线性问题,相比传统EKF具有更好的数值稳定性和精度
- 实现了IMU与GNSS的有效融合,充分发挥两种传感器的互补优势
状态模型
8维误差状态模型:
位置:2维(X, Y坐标)
速度:2维(X, Y方向速度)
航向角:1维(偏航角yaw)
陀螺仪偏差:1维(角速度偏差)
加速度计偏差:2维(X, Y方向加速度偏差)
观测模型
2维观测:GNSS提供的XY位置信息
观测频率:GNSS每1秒更新一次(10Hz IMU,1Hz GNSS)
核心算法
容积卡尔曼滤波器:采用球面-径向积分规则,通过2n个容积点来近似状态分布
非线性系统处理:能够有效处理姿态更新中的非线性问题
仿真场景
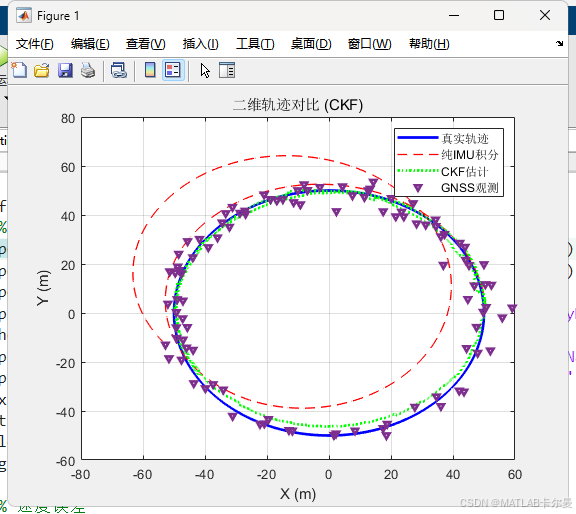
轨迹类型:圆形运动
运动参数:
半径:50米
角速度:0.1 rad/s
仿真时间:100秒
采样频率:10Hz
噪声模型
IMU噪声:
陀螺仪噪声:0.1°/s
加速度计噪声:0.01 m/s²
陀螺仪偏差:0.01°/s
加速度计偏差:0.001 m/s²
GNSS噪声:
位置测量噪声:3米标准差
运行结果
轨迹对比:
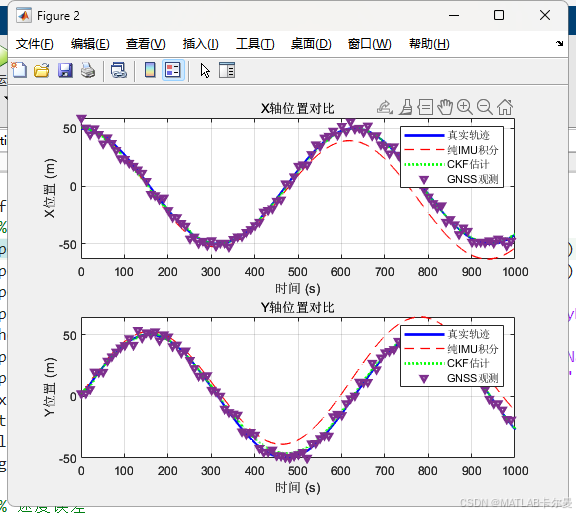
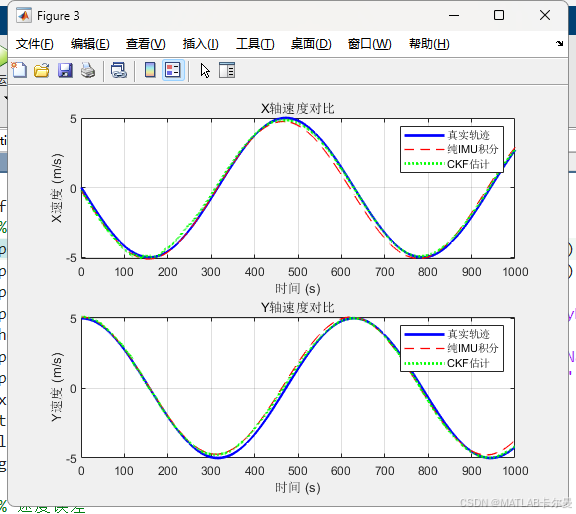
两轴的位置对比和速度对比:
误差对比曲线: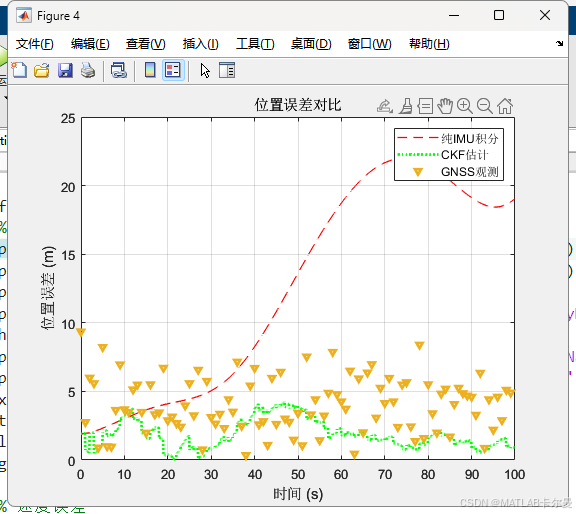
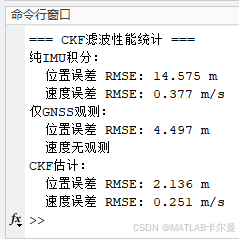
命令行窗口的截图:
MATLAB源代码
部分代码如下:
matlab
% 平面CKF例程(严格的组合导航推导),82
% 基于8维误差状态模型:位置(2)、速度(2)、航向角、航向偏差(1)、加速度计偏差(2)
% 基于4维观测:XY位置(2)
% 容积卡尔曼滤波器(Cubature Kalman Filter)实现
% 作者:matlabfilter
% 2025-08-30/Ver1
clear; clc; close all;
rng(0); % 固定随机种子
%% 系统参数设置
dt = 0.1; % 采样时间间隔 (s)
total_time = 100; % 总仿真时间 (s)
N = total_time / dt; % 采样点数
%% 噪声参数设置
% IMU噪声参数
gyro_noise_std = 0.1 * pi/180; % 陀螺噪声标准差 (rad/s)
accel_noise_std = 0.01; % 加速度计噪声标准差 (m/s^2)
gyro_bias_std = 0.01 * pi/180; % 陀螺偏差标准差 (rad/s)
accel_bias_std = 0.001; % 加速度计偏差标准差 (m/s^2)
% GNSS观测噪声
gnss_pos_noise_std = 3; % GNSS位置噪声标准差 (m)
gnss_vel_noise_std = 0.1; % GNSS速度噪声标准差 (m/s)
%% 过程噪声协方差矩阵Q (8×8)
% 状态顺序:[位置(2), 速度(2), 姿态(1), 陀螺偏差(1), 加速度计偏差(2)]
Q = zeros(8, 8);
% 位置噪声(通过速度积分产生)
Q(1:2, 1:2) = eye(2) * (accel_noise_std * dt^2)^2;
% 速度噪声
Q(3:4, 3:4) = eye(2) * (accel_noise_std * dt)^2;
% 姿态噪声
Q(5, 5) = eye(1) * (gyro_noise_std * dt)^2;
% 陀螺偏差噪声
Q(6, 6) = eye(1) * (gyro_bias_std * dt)^2;
% 加速度计偏差噪声
Q(7:8, 7:8) = eye(2) * (accel_bias_std * dt)^2;
%% 观测噪声协方差矩阵R (4×4)
% 观测量:GNSS位置(2)
R = eye(2) * gnss_pos_noise_std^2;完整代码:
https://download.csdn.net/download/callmeup/92007983
或查看专栏文章:
- 组合导航的MATLAB代码,二维平面上的CKF滤波,融合IMU和GNSS数据,仿真,观测为X和Y轴的坐标:https://blog.csdn.net/callmeup/article/details/152035022?spm=1011.2415.3001.5331
如需帮助,或有导航、定位滤波相关的代码定制需求,请点击下方卡片联系作者