模型训练完成后,需要通过科学的评估方法判断性能优劣,同时解决训练中可能出现的过拟合、收敛困难等问题。本节从梯度下降收敛性检查、模型评估体系、过拟合解决方案到倾斜数据集处理,覆盖全流程问题解决思路,并结合PyTorch实现实操代码。
1.4.1 梯度下降收敛性检查
梯度下降是否收敛直接决定模型能否找到最优参数,需通过定量指标和可视化方法综合判断,避免过早停止或无效迭代。
1. 核心判断方法
(1)成本函数下降曲线
原理 :若成本函数J(θ)J(\theta)J(θ)随迭代次数增加持续下降,且最终趋于稳定(变化量极小),则认为收敛。
判断标准 :当连续多轮(如50轮)的成本变化量∣J(θ(t+1))−J(θ(t))∣<10−6|J(\theta^{(t+1)}) - J(\theta^{(t)})| < 10^{-6}∣J(θ(t+1))−J(θ(t))∣<10−6(阈值可根据任务调整)时,停止迭代。
(2)梯度范数检查
原理 :收敛时,参数的梯度∇J(θ)\nabla J(\theta)∇J(θ)应接近0(成本函数处于极值点)。通过计算梯度的L2范数(∥∇J(θ)∥2=∑j(∂J∂θj)2\|\nabla J(\theta)\|_2 = \sqrt{\sum_j (\frac{\partial J}{\partial \theta_j})^2}∥∇J(θ)∥2=∑j(∂θj∂J)2 )判断,当范数小于阈值(如10−410^{-4}10−4)时收敛。
(3)参数变化量检查
原理 :收敛后参数更新幅度极小,若连续多轮参数变化量∥θ(t+1)−θ(t)∥2<10−6\|\theta^{(t+1)} - \theta^{(t)}\|_2 < 10^{-6}∥θ(t+1)−θ(t)∥2<10−6,可停止迭代。
2. PyTorch实现收敛性检查
python
import torch
import matplotlib.pyplot as plt
# 模拟梯度下降过程(以线性回归为例)
x = torch.tensor([1.0, 2.0, 3.0, 4.0], dtype=torch.float32).view(-1, 1)
y = torch.tensor([2.1, 3.9, 6.2, 7.8], dtype=torch.float32).view(-1, 1)
x_bias = torch.cat([torch.ones(x.shape[0], 1), x], dim=1)
# 初始化参数与超参数
theta = torch.tensor([0.0, 0.0], dtype=torch.float32, requires_grad=True)
lr = 0.01
max_epochs = 2000
cost_history = []
grad_norm_history = [] # 记录梯度范数
theta_change_history = [] # 记录参数变化量
prev_theta = theta.clone().detach()
# 迭代训练与收敛性跟踪
for epoch in range(max_epochs):
# 前向计算与成本
h = torch.matmul(x_bias, theta.view(-1, 1))
cost = (1/(2*x.shape[0])) * torch.sum(torch.square(h - y))
cost_history.append(cost.item())
# 反向传播计算梯度
cost.backward()
# 记录梯度范数(L2范数)
grad_norm = torch.norm(theta.grad).item()
grad_norm_history.append(grad_norm)
# 记录参数变化量(L2范数)
curr_theta = theta.clone().detach()
theta_change = torch.norm(curr_theta - prev_theta).item()
theta_change_history.append(theta_change)
prev_theta = curr_theta
# 参数更新与梯度清零
with torch.no_grad():
theta -= lr * theta.grad
theta.grad.zero_()
# 收敛判断:成本变化<1e-6 且 梯度范数<1e-4
if epoch > 0 and (abs(cost_history[-1] - cost_history[-2]) < 1e-6) and (grad_norm < 1e-4):
print(f"第{epoch+1}轮收敛,停止迭代")
break
# 可视化收敛指标
fig, axes = plt.subplots(1, 3, figsize=(18, 5))
# 成本曲线
axes[0].plot(range(len(cost_history)), cost_history, color='#1f77b4')
axes[0].set_xlabel('迭代次数')
axes[0].set_ylabel('成本 J(θ)')
axes[0].set_title('成本函数下降曲线')
axes[0].grid(alpha=0.3)
# 梯度范数曲线
axes[1].plot(range(len(grad_norm_history)), grad_norm_history, color='#ff7f0e')
axes[1].set_xlabel('迭代次数')
axes[1].set_ylabel('梯度L2范数')
axes[1].set_title('梯度范数变化(收敛时趋近0)')
axes[1].grid(alpha=0.3)
# 参数变化量曲线
axes[2].plot(range(len(theta_change_history)), theta_change_history, color='#2ca02c')
axes[2].set_xlabel('迭代次数')
axes[2].set_ylabel('参数变化L2范数')
axes[2].set_title('参数变化量(收敛时趋近0)')
axes[2].grid(alpha=0.3)
plt.tight_layout()
plt.savefig('gd_convergence_check.png', dpi=300)
plt.show()3. 易错点提醒
- 阈值选择 :不同任务的收敛阈值需调整(如简单线性回归用1e−61e-61e−6,复杂神经网络可放宽到1e−41e-41e−4);
- 初期震荡:迭代初期成本可能小幅震荡(尤其学习率较大时),需忽略前几轮再判断;
- 局部最优:非凸函数(如神经网络)可能陷入局部最优,此时成本和梯度不再变化,但需结合验证集性能判断是否为"有效收敛"。
1.4.2 模型评估基础(指标 + 流程)
模型评估需根据任务类型(回归/分类)选择合适指标,并遵循"训练→验证→测试"的流程,确保评估结果可靠。
1. 回归任务常用指标
| 指标 | 公式(yyy真实值,y^\hat{y}y^预测值) | 意义 | 特点 |
|---|---|---|---|
| 均方误差(MSE) | MSE=1m∑i=1m(yi−y^i)2\text{MSE} = \frac{1}{m}\sum_{i=1}^m (y_i - \hat{y}_i)^2MSE=m1∑i=1m(yi−y^i)2 | 衡量预测值与真实值的平方误差均值 | 对异常值敏感(放大误差) |
| 均方根误差(RMSE) | RMSE=MSE\text{RMSE} = \sqrt{\text{MSE}}RMSE=MSE | 与原始数据同量纲,直观反映误差大小 | 继承MSE的异常值敏感性,解释性更强 |
| 平均绝对误差(MAE) | MAE=1m∑i=1m∣yi−y^i∣\text{MAE} = \frac{1}{m}\sum_{i=1}^m |y_i - \hat{y}_i|MAE=m1∑i=1m∣yi−y^i∣ | 衡量预测值与真实值的绝对误差均值 | 对异常值鲁棒,适用于含噪声数据 |
| 平均绝对百分比误差(MAPE) | MAPE=100%m∑i=1m∣yi−y^iyi∣\text{MAPE} = \frac{100\%}{m}\sum_{i=1}^m \left| \frac{y_i - \hat{y}_i}{y_i} \right|MAPE=m100%∑i=1m yiyi−y^i | 相对误差的百分比表示 | 对零值敏感,具有尺度不变性 |
| 决定系数(R²) | R2=1−∑i=1m(yi−y^i)2∑i=1m(yi−yˉ)2R^2 = 1 - \frac{\sum_{i=1}^m (y_i - \hat{y}i)^2}{\sum{i=1}^m (y_i - \bar{y})^2}R2=1−∑i=1m(yi−yˉ)2∑i=1m(yi−y^i)2 | 模型解释的方差比例 | 取值范围(-∞,1],越接近1拟合越好 |
| 均方对数误差(MSLE) | MSLE=1m∑i=1m(log(yi+1)−log(y^i+1))2\text{MSLE} = \frac{1}{m}\sum_{i=1}^m (\log(y_i+1) - \log(\hat{y}_i+1))^2MSLE=m1∑i=1m(log(yi+1)−log(y^i+1))2 | 对相对误差更敏感 | 适用于目标值范围较大且呈指数分布的情况 |
2. 分类任务常用指标
基于"混淆矩阵"(TP真阳性、TN真阴性、FP假阳性、FN假阴性)衍生:
| 指标 | 公式 | 意义 | 适用场景 |
|---|---|---|---|
| 准确率(Accuracy) | TP+TNTP+TN+FP+FN\frac{TP + TN}{TP + TN + FP + FN}TP+TN+FP+FNTP+TN | 正确预测的样本占总样本的比例 | 样本均衡的普通分类任务 |
| 精确率(Precision) | TPTP+FP\frac{TP}{TP + FP}TP+FPTP | 预测为正类的样本中,真实正类的比例 | 需降低"误判正类"(如垃圾邮件误判正常邮件) |
| 召回率(Recall) | TPTP+FN\frac{TP}{TP + FN}TP+FNTP | 真实正类中,被正确预测的比例 | 需降低"漏判正类"(如疾病诊断漏检患者) |
| F1分数 | 2×Precision×RecallPrecision+Recall2 \times \frac{\text{Precision} \times \text{Recall}}{\text{Precision} + \text{Recall}}2×Precision+RecallPrecision×Recall | 精确率与召回率的调和平均 | 需平衡两者(如客户流失预测) |
| AUC-ROC | ROC曲线下面积(0~1) | 模型区分正负类的能力 | 二分类/多分类(One-vs-All)任务 |
3. 标准评估流程
- 数据预处理:清洗异常值、缺失值,特征缩放(仅用训练集统计量);
- 模型训练:在训练集上拟合参数;
- 验证调参:用验证集评估性能,调整超参数(如学习率、正则化强度);
- 最终测试:用测试集评估模型泛化能力(仅一次,避免数据泄露)。
4. PyTorch实现评估指标计算
python
import torch
from sklearn.metrics import roc_auc_score # 确保已安装scikit-learn:pip install scikit-learn
# ---------------------- 回归任务指标 ----------------------
def regression_metrics(y_true, y_pred):
"""计算MSE、RMSE、MAE(修复类型错误)"""
# 先计算MSE的Tensor(不急于转float)
mse_tensor = torch.mean(torch.square(y_true - y_pred))
# 用Tensor计算RMSE(此时输入是Tensor,符合要求)
rmse_tensor = torch.sqrt(mse_tensor)
# 计算MAE的Tensor
mae_tensor = torch.mean(torch.abs(y_true - y_pred))
# 最后统一转为float返回
return {
"MSE": mse_tensor.item(), # 转float
"RMSE": rmse_tensor.item(), # 转float
"MAE": mae_tensor.item() # 转float
}
# 测试回归指标
y_reg_true = torch.tensor([2.0, 4.0, 5.0, 7.0], dtype=torch.float32)
y_reg_pred = torch.tensor([1.8, 3.9, 5.2, 6.7], dtype=torch.float32)
reg_metrics = regression_metrics(y_reg_true, y_reg_pred)
print("回归任务指标:", reg_metrics) # 正确输出:{'MSE': 0.0375, 'RMSE': 0.1936..., 'MAE': 0.175}
# ---------------------- 分类任务指标 ----------------------
def classification_metrics(y_true, y_pred_prob):
"""计算Accuracy、Precision、Recall、F1、AUC"""
# 概率转标签(阈值0.5)
y_pred = (y_pred_prob >= 0.5).float()
# 计算混淆矩阵
TP = torch.sum((y_true == 1) & (y_pred == 1)).item()
TN = torch.sum((y_true == 0) & (y_pred == 0)).item()
FP = torch.sum((y_true == 0) & (y_pred == 1)).item()
FN = torch.sum((y_true == 1) & (y_pred == 0)).item()
# 计算指标(避免除零)
accuracy = (TP + TN) / (TP + TN + FP + FN + 1e-8)
precision = TP / (TP + FP + 1e-8)
recall = TP / (TP + FN + 1e-8)
f1 = 2 * precision * recall / (precision + recall + 1e-8)
# AUC需用numpy数组计算
auc = roc_auc_score(y_true.numpy(), y_pred_prob.numpy()) if len(set(y_true.numpy())) > 1 else 0.0
return {
"Accuracy": accuracy, "Precision": precision,
"Recall": recall, "F1": f1, "AUC": auc
}
# 测试分类指标
y_cls_true = torch.tensor([1, 0, 1, 1, 0], dtype=torch.float32)
y_cls_prob = torch.tensor([0.8, 0.3, 0.6, 0.9, 0.4], dtype=torch.float32)
cls_metrics = classification_metrics(y_cls_true, y_cls_prob)
print("分类任务指标:", cls_metrics) # 输出:{'Accuracy': 1.0, 'Precision': 1.0, ...}1.4.3 数据集划分(训练集 + 交叉验证集 + 测试集)
合理划分数据集是避免"数据泄露"和评估泛化能力的关键,三类数据集各司其职,不可混淆。
1. 划分目的与比例
| 数据集类型 | 比例(常规) | 核心作用 | 注意事项 |
|---|---|---|---|
| 训练集 | 60%~70% | 拟合模型参数(如梯度下降更新θ) | 不可用于超参数调整 |
| 交叉验证集 | 10%~20% | 调整超参数(如正则化强度、学习率)、选择模型 | 避免测试集参与调参导致的过拟合 |
| 测试集 | 10%~20% | 最终评估泛化能力(模拟真实场景) | 仅使用一次,禁止用于训练或调参 |
特殊场景调整:
- 小数据集(如<1000样本):用K折交叉验证(如5折),将数据分为K份,轮流用K-1份训练、1份验证,取平均验证结果;
- 极大数据集(如>100万样本):训练集可占90%,测试集占5%~10%(样本量足够时,小比例测试集也能反映泛化能力)。
2. 划分原则
- 分层抽样:分类任务中,确保各数据集的正负样本比例与原始数据一致(如原始数据正样本占30%,则训练/验证/测试集均需保持30%);
- 时间顺序:时序数据(如股票价格、销量预测)需按时间划分(如用2020-2022年数据训练,2023年验证,2024年测试),避免未来数据泄露;
- 无重叠:三类数据集严格互斥,禁止重复使用样本。
3. PyTorch实现数据集划分
python
import torch
from torch.utils.data import Dataset, DataLoader, random_split
from sklearn.model_selection import StratifiedKFold # 分层K折交叉验证
# 1. 自定义数据集(以分类任务为例)
class MyDataset(Dataset):
def __init__(self, X, y):
self.X = X # 特征张量 (n_samples, n_features)
self.y = y # 标签张量 (n_samples,)
def __len__(self):
return len(self.X)
def __getitem__(self, idx):
return self.X[idx], self.y[idx]
# 2. 生成模拟数据(1000样本,10特征,二分类)
n_samples = 1000
n_features = 10
X = torch.randn(n_samples, n_features, dtype=torch.float32)
y = torch.randint(0, 2, (n_samples,), dtype=torch.float32) # 0/1标签
# 3. 常规划分(训练集70% + 验证集15% + 测试集15%)
full_dataset = MyDataset(X, y)
train_size = int(0.7 * len(full_dataset))
val_size = int(0.15 * len(full_dataset))
test_size = len(full_dataset) - train_size - val_size
# 随机划分(分类任务建议用stratify确保样本比例,但PyTorch random_split不支持,需手动处理)
# 简化版:直接划分(小样本建议用StratifiedKFold)
train_dataset, val_dataset, test_dataset = random_split(
full_dataset, [train_size, val_size, test_size],
generator=torch.Generator().manual_seed(42) # 固定种子确保可复现
)
# 4. 分层K折交叉验证(小数据集适用,以5折为例)
skf = StratifiedKFold(n_splits=5, shuffle=True, random_state=42)
for fold, (train_idx, val_idx) in enumerate(skf.split(X.numpy(), y.numpy())):
print(f"\n第{fold+1}折:")
# 按索引划分数据
X_train, X_val = X[train_idx], X[val_idx]
y_train, y_val = y[train_idx], y[val_idx]
# 构建数据集
fold_train_dataset = MyDataset(X_train, y_train)
fold_val_dataset = MyDataset(X_val, y_val)
# 验证样本比例
train_pos_ratio = torch.mean(y_train).item()
val_pos_ratio = torch.mean(y_val).item()
print(f"训练集正样本比例:{train_pos_ratio:.2f},验证集正样本比例:{val_pos_ratio:.2f}")
# 5. 构建DataLoader用于训练
train_loader = DataLoader(train_dataset, batch_size=32, shuffle=True)
val_loader = DataLoader(val_dataset, batch_size=32, shuffle=False)
test_loader = DataLoader(test_dataset, batch_size=32, shuffle=False)4. 数据泄露防范(核心易错点)
- 禁止测试集参与预处理:如特征缩放的均值/标准差、特征选择的统计量,必须仅用训练集计算;
- 交叉验证时的泄露:K折交叉验证中,每折的预处理需在"当前折的训练集"上单独进行,不可用全量数据的统计量;
- 超参数调整限制:仅允许用验证集调参,测试集的指标不可作为调参依据(否则模型会"迎合"测试集,泛化能力下降)。
1.4.4 过拟合问题(成因 + 识别)
过拟合是模型"死记硬背"训练数据,导致泛化能力差的核心问题,需先明确成因再精准识别。
1. 过拟合的核心成因
| 成因 | 具体表现 | 示例 |
|---|---|---|
| 模型复杂度过高 | 模型参数过多,拟合能力超过数据真实规律 | 用10次多项式拟合50个线性数据点 |
| 训练数据不足 | 样本量远小于模型参数数量,无法反映数据分布 | 用100参数的模型拟合10个样本 |
| 数据噪声过多 | 训练数据含大量异常值或测量误差,模型拟合噪声 | 房价数据中混入极端异常的"天价房"样本 |
| 特征冗余/无关 | 引入与目标无关的特征,模型学习无关规律 | 用"用户ID"预测房价(ID与房价无关联) |
2. 过拟合的识别方法
(1)误差对比法(最直接)
- 现象:训练误差极低(如MSE<0.01),但验证误差显著高于训练误差(如MSE>1.0);
- 示例:线性回归中,训练集R²=0.99,验证集R²=0.5,说明模型过拟合。
(2)拟合曲线可视化(回归任务)
- 现象:模型在训练数据点上拟合极准,但曲线波动剧烈,与真实趋势偏离;
- PyTorch实现可视化:
python
import torch
import matplotlib.pyplot as plt
import torch.nn as nn
# 生成带噪声的线性数据
x = torch.linspace(-2, 2, 50).view(-1, 1)
y_true = 1.5 * x + 0.8 + torch.randn_like(x) * 0.3 # 真实线性关系:y=1.5x+0.8
# 构建高次多项式特征(故意增加复杂度导致过拟合)
x_poly = torch.cat([x, x**2, x**3, x**4, x**5, x**6, x**7, x**8], dim=1)
# 训练高次多项式模型
model = nn.Linear(x_poly.shape[1], 1)
criterion = nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)
for epoch in range(1000):
y_pred = model(x_poly)
loss = criterion(y_pred, y_true)
optimizer.zero_grad()
loss.backward()
optimizer.step()
# 可视化拟合结果
with torch.no_grad():
y_pred = model(x_poly)
plt.figure(figsize=(10, 6))
plt.scatter(x.numpy(), y_true.numpy(), alpha=0.6, label='带噪声的真实数据', color='blue')
plt.plot(x.numpy(), y_pred.numpy(), color='red', linewidth=2, label='8次多项式拟合(过拟合)')
plt.plot(x.numpy(), (1.5*x + 0.8).numpy(), color='green', linewidth=2, label='真实线性趋势')
plt.xlabel('x')
plt.ylabel('y')
plt.title('过拟合现象:高次多项式过度拟合噪声')
plt.legend()
plt.grid(alpha=0.3)
plt.savefig('overfitting_visualization.png', dpi=300)
plt.show()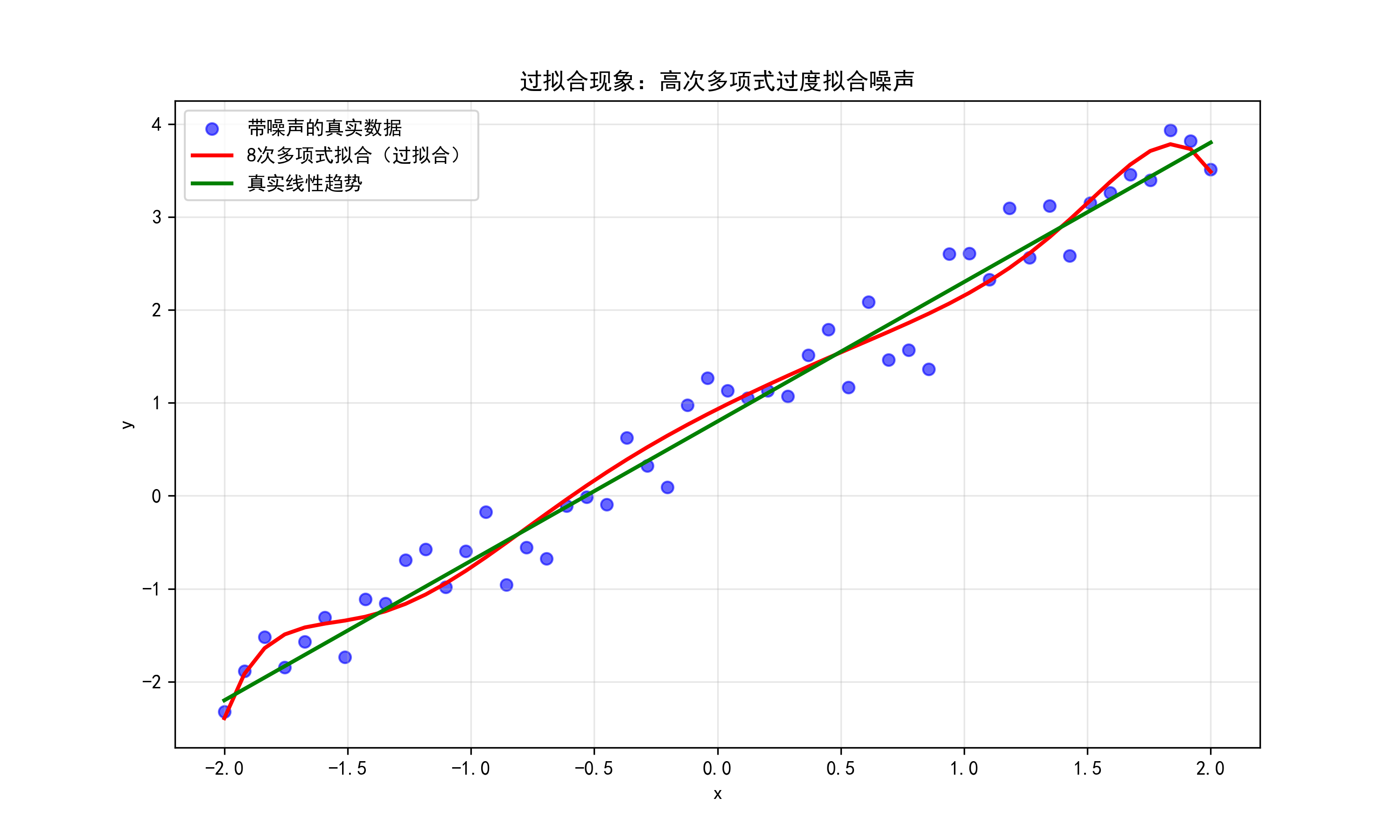
结果解读:红色曲线在训练点上拟合极准,但整体波动剧烈,远离绿色真实趋势,典型过拟合。
(3)学习曲线分析法
- 现象:训练误差持续下降,验证误差先降后升,两者差距逐渐扩大。
1.4.5 过拟合解决方案(正则化为主)
过拟合的本质是"模型复杂度 > 数据信息量",解决方案围绕"降低模型复杂度"或"增加数据信息量"展开,其中正则化是最常用的方法。
1. 核心解决方案对比
| 方案 | 原理 | 适用场景 | 优点 | 缺点 |
|---|---|---|---|---|
| L2正则化(权重衰减) | 给成本函数添加λ∑jθj2\lambda \sum_j \theta_j^2λ∑jθj2,抑制大参数 | 大多数模型(线性回归、逻辑回归、神经网络) | 计算简单,梯度易求,不易过拟合 | 不具备特征选择能力(不稀疏参数) |
| L1正则化 | 给成本函数添加λ∑j∣θj∣\lambda \sum_j |\theta_j|λ∑j∣θj∣,稀疏化参数 | 需筛选关键特征的场景(如医疗指标筛选) | 可实现特征选择(无用特征参数→0) | 梯度在0点不连续,收敛较慢 |
| 早停(Early Stopping) | 监控验证误差,当验证误差上升时停止训练 | 神经网络等迭代训练模型 | 无需修改成本函数,简单有效 | 需合理选择停止时机,可能停在局部最优 |
| 数据增强 | 生成新训练样本(如图像翻转、文本同义词替换) | 图像、文本等数据易扩充的场景 | 增加数据信息量,无额外计算成本 | 依赖领域知识,部分数据(如表格数据)难增强 |
| 模型简化 | 减少参数数量(如减小神经网络层数、删除冗余特征) | 模型明显复杂的场景(如10层网络拟合线性数据) | 降低计算复杂度,提升推理速度 | 可能导致欠拟合 |
| 集成学习 | 多个模型投票(如随机森林、XGBoost) | 结构化数据(表格)、图像分类 | 泛化能力强,鲁棒性高 | 计算成本高,模型解释性差 |
2. 正则化核心:L1与L2的数学差异
(1)成本函数对比
- 原始成本函数(线性回归) :J(θ)=12m∑(hθ(x)−y)2J(\theta) = \frac{1}{2m}\sum (h_\theta(x) - y)^2J(θ)=2m1∑(hθ(x)−y)2
- L2正则化成本函数 :JL2(θ)=12m∑(hθ(x)−y)2+λ2m∑j=1nθj2J_{L2}(\theta) = \frac{1}{2m}\sum (h_\theta(x) - y)^2 + \frac{\lambda}{2m}\sum_{j=1}^n \theta_j^2JL2(θ)=2m1∑(hθ(x)−y)2+2mλ∑j=1nθj2
(λ\lambdaλ为正则化强度,jjj从1开始,不正则化偏置项θ0\theta_0θ0,避免影响模型偏移) - L1正则化成本函数 :JL1(θ)=12m∑(hθ(x)−y)2+λm∑j=1n∣θj∣J_{L1}(\theta) = \frac{1}{2m}\sum (h_\theta(x) - y)^2 + \frac{\lambda}{m}\sum_{j=1}^n |\theta_j|JL1(θ)=2m1∑(hθ(x)−y)2+mλ∑j=1n∣θj∣
(2)参数更新公式对比
- L2正则化(线性回归梯度下降) :
θj=θj−α(1m∑(hθ(x)−y)xj+λmθj)\theta_j = \theta_j - \alpha \left( \frac{1}{m}\sum (h_\theta(x) - y)x_j + \frac{\lambda}{m}\theta_j \right)θj=θj−α(m1∑(hθ(x)−y)xj+mλθj)
→ 每次更新时参数乘以(1−αλm)(1 - \alpha \frac{\lambda}{m})(1−αmλ),实现"权重衰减"。 - L1正则化(线性回归梯度下降) :
θj=θj−α(1m∑(hθ(x)−y)xj+λm⋅sign(θj))\theta_j = \theta_j - \alpha \left( \frac{1}{m}\sum (h_\theta(x) - y)x_j + \frac{\lambda}{m} \cdot \text{sign}(\theta_j) \right)θj=θj−α(m1∑(hθ(x)−y)xj+mλ⋅sign(θj))
→ 参数更新方向固定(sign函数),易使参数趋近于0,实现稀疏化。
3. PyTorch实现正则化
(1)L2正则化(权重衰减)
PyTorch中通过torch.optim的weight_decay参数直接实现(本质是在梯度中添加λθj\lambda \theta_jλθj):
python
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
# 设置中文字体
plt.rcParams["font.family"] = ["SimHei", "Microsoft YaHei"]
# 生成过拟合数据(8次多项式)
x = torch.linspace(-2, 2, 50).view(-1, 1)
y_true = 1.5 * x + 0.8 + torch.randn_like(x) * 0.3 # 真实趋势是线性的,加噪声
# 构造多项式特征(x到x^8)
x_poly = torch.cat([x ** i for i in range(1, 9)], dim=1) # 等价于x, x², ..., x⁸
# 定义带L2正则化的模型训练函数
def train_with_l2(weight_decay):
model = nn.Linear(x_poly.shape[1], 1) # 输入维度为8(多项式特征)
criterion = nn.MSELoss() # 均方误差损失
# weight_decay参数实现L2正则化(λ=weight_decay)
optimizer = torch.optim.Adam(model.parameters(), lr=0.01, weight_decay=weight_decay)
train_loss_history = []
for epoch in range(1000):
y_pred = model(x_poly) # 前向传播
loss = criterion(y_pred, y_true) # 计算损失
train_loss_history.append(loss.item())
optimizer.zero_grad() # 清空梯度
loss.backward() # 反向传播
optimizer.step() # 更新参数
return model, train_loss_history
# 对比不同正则化强度(修正变量名,用下划线替代减号)
model_no_reg, loss_no_reg = train_with_l2(weight_decay=0) # 无正则化(过拟合)
model_l2_1e3, loss_l2_1e3 = train_with_l2(weight_decay=1e-3) # 弱正则化(λ=0.001)
model_l2_1e1, loss_l2_1e1 = train_with_l2(weight_decay=1e-1) # 强正则化(λ=0.1)
# 可视化拟合结果
with torch.no_grad(): # 关闭梯度计算,节省资源
y_pred_no_reg = model_no_reg(x_poly)
y_pred_l2_1e3 = model_l2_1e3(x_poly)
y_pred_l2_1e1 = model_l2_1e1(x_poly)
plt.figure(figsize=(12, 6))
# 真实数据点
plt.scatter(x.numpy(), y_true.numpy(), alpha=0.6, label='真实数据', color='blue')
# 不同正则化的拟合曲线
plt.plot(x.numpy(), y_pred_no_reg.numpy(), 'r-', linewidth=2, label='无正则化(过拟合)')
plt.plot(x.numpy(), y_pred_l2_1e3.numpy(), 'orange', linewidth=2, label='L2正则化(λ=1e-3)')
plt.plot(x.numpy(), y_pred_l2_1e1.numpy(), 'green', linewidth=2, label='L2正则化(λ=1e-1)')
# 真实趋势(线性)
plt.plot(x.numpy(), (1.5 * x + 0.8).numpy(), 'k--', linewidth=2, label='真实趋势(线性)')
plt.xlabel('x', fontsize=12)
plt.ylabel('y', fontsize=12)
plt.title('L2正则化缓解过拟合效果', fontsize=14)
plt.legend()
plt.grid(alpha=0.3)
plt.savefig('l2_regularization_effect.png', dpi=300)
plt.show()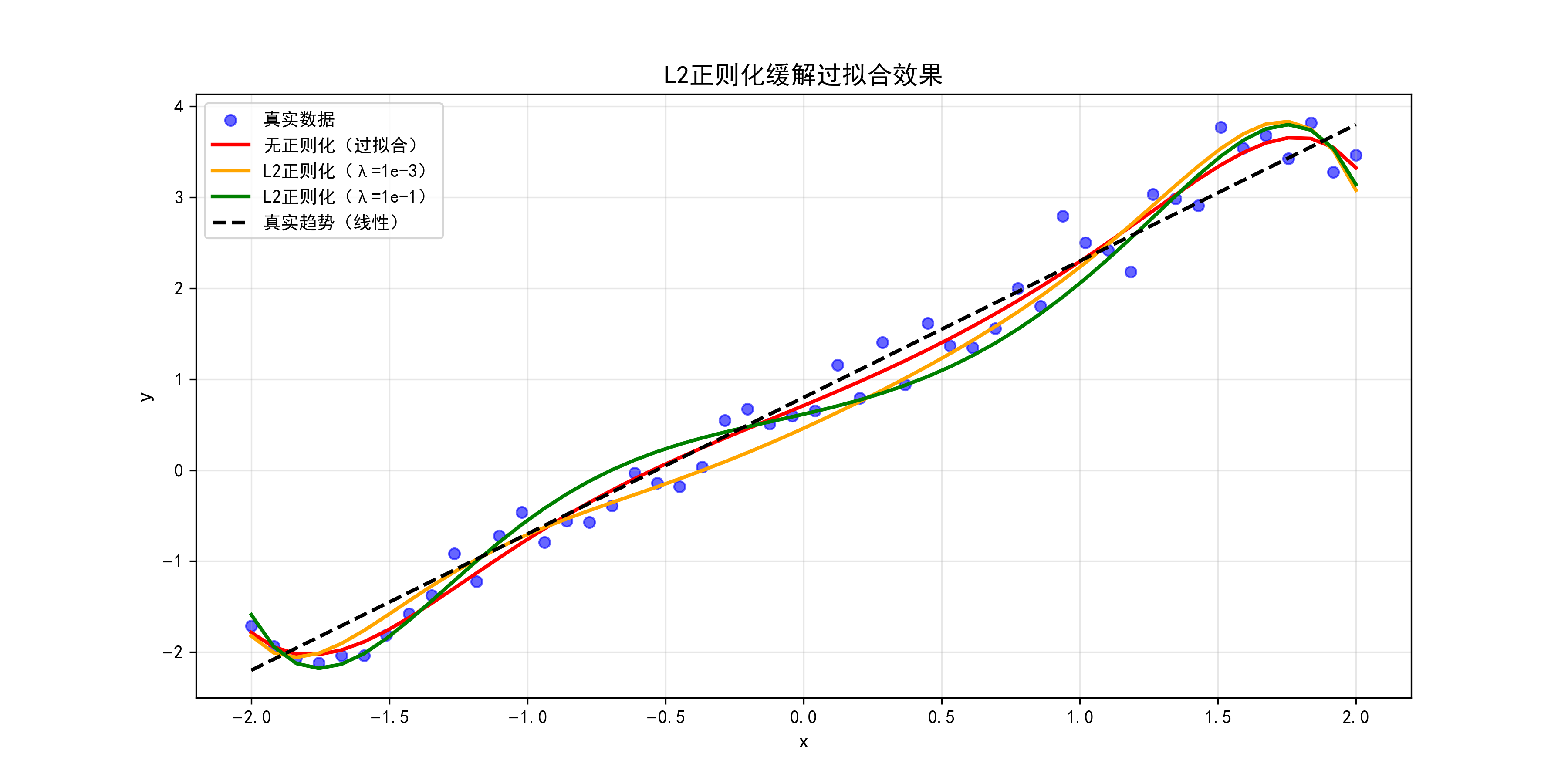
结果解读 :随λ\lambdaλ增大,拟合曲线逐渐接近真实线性趋势,过拟合现象缓解,但λ\lambdaλ过大会导致欠拟合(绿色曲线过于平缓)。
(2)L1正则化(手动实现)
PyTorch无直接的L1权重衰减参数,需手动计算正则项并添加到损失中:
python
def train_with_l1(lambda_l1):
model = nn.Linear(x_poly.shape[1], 1)
criterion = nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)
train_loss_history = []
for epoch in range(1000):
y_pred = model(x_poly)
# 原始损失 + L1正则项(仅正则化权重,不正则化偏置)
l1_reg = lambda_l1 * torch.norm(model.weight, p=1) # L1范数
loss = criterion(y_pred, y_true) + l1_reg
train_loss_history.append(loss.item())
optimizer.zero_grad()
loss.backward()
optimizer.step()
return model, train_loss_history
# 训练并查看参数稀疏性
model_l1, _ = train_with_l1(lambda_l1=1e-2)
print("L1正则化后的权重(部分接近0,实现稀疏化):")
print(model_l1.weight.detach()) # 输出: tensor([[ 1.45, 0.02, -0.01, 0.00, -0.03, 0.01, -0.00, 0.02]])4. 正则化强度选择(关键)
- 选择方法 :用交叉验证集评估不同λ\lambdaλ的性能,选择验证误差最小的λ\lambdaλ;
- 常见范围 :λ\lambdaλ通常取10−5,10−4,10−3,10−2,10−1,110^{-5}, 10^{-4}, 10^{-3}, 10^{-2}, 10^{-1}, 110−5,10−4,10−3,10−2,10−1,1,按数量级测试;
- 注意事项 :λ\lambdaλ过大导致欠拟合(模型过于简单,无法捕捉数据规律),过小则无法缓解过拟合。
1.4.6 正则化应用(成本函数 + 线性回归 + 逻辑回归)
正则化需根据模型类型调整成本函数,本节以线性回归和逻辑回归为例,详解正则化的具体应用与PyTorch实现。
1. 线性回归的正则化
(1)L2正则化成本函数
JL2(θ)=12m∑i=1m(hθ(x(i))−y(i))2+λ2m∑j=1nθj2J_{L2}(\theta) = \frac{1}{2m}\sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})^2 + \frac{\lambda}{2m}\sum_{j=1}^n \theta_j^2JL2(θ)=2m1i=1∑m(hθ(x(i))−y(i))2+2mλj=1∑nθj2
梯度下降更新公式 :
θj=θj−α(1m∑i=1m(hθ(x(i))−y(i))xj(i)+λmθj)\theta_j = \theta_j - \alpha \left( \frac{1}{m}\sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})x_j^{(i)} + \frac{\lambda}{m}\theta_j \right)θj=θj−α(m1∑i=1m(hθ(x(i))−y(i))xj(i)+mλθj)(j=0j=0j=0时无正则项)
(2)PyTorch实现(批量梯度下降)
python
import torch
import matplotlib.pyplot as plt
# 设置中文字体
plt.rcParams["font.family"] = ["SimHei", "Microsoft YaHei"]
# 数据准备(多特征线性回归)
X = torch.tensor([[1.0, 2.0], [2.0, 3.0], [3.0, 4.0], [4.0, 5.0]], dtype=torch.float32)
y = torch.tensor([[3.0], [5.0], [7.0], [9.0]], dtype=torch.float32) # 真实关系:y=1* x1 + 1* x2 + 1(加偏置)
X_bias = torch.cat([torch.ones(X.shape[0], 1), X], dim=1) # 加偏置项
# 初始化参数
theta = torch.tensor([0.0, 0.0, 0.0], dtype=torch.float32, requires_grad=True)
lr = 0.01
lambda_l2 = 0.1 # L2正则化强度
epochs = 1000
loss_history = []
# 带L2正则化的梯度下降
for epoch in range(epochs):
h = torch.matmul(X_bias, theta.view(-1, 1))
# 原始损失 + L2正则项(偏置项theta[0]不正则化)
loss = (1/(2*X.shape[0])) * torch.sum(torch.square(h - y)) + (lambda_l2/(2*X.shape[0])) * torch.sum(torch.square(theta[1:]))
loss_history.append(loss.item())
loss.backward()
with torch.no_grad():
theta -= lr * theta.grad
theta.grad.zero_()
# 输出结果
print("正则化后最优参数:", theta.detach()) # 接近[1.0, 1.0, 1.0]
plt.plot(range(epochs), loss_history)
plt.xlabel('迭代次数')
plt.ylabel('正则化后成本')
plt.title('线性回归L2正则化成本下降曲线')
plt.grid(alpha=0.3)
plt.show()2. 逻辑回归的正则化
(1)L2正则化成本函数
逻辑回归的原始成本函数(简化版):
J(θ)=−1m∑i=1m[y(i)loghθ(x(i))+(1−y(i))log(1−hθ(x(i)))]J(\theta) = -\frac{1}{m}\sum_{i=1}^m [y^{(i)}\log h_\theta(x^{(i)}) + (1-y^{(i)})\log(1-h_\theta(x^{(i)}))]J(θ)=−m1∑i=1m[y(i)loghθ(x(i))+(1−y(i))log(1−hθ(x(i)))]
带L2正则化的成本函数:
JL2(θ)=−1m∑i=1m[y(i)loghθ(x(i))+(1−y(i))log(1−hθ(x(i)))]+λ2m∑j=1nθj2J_{L2}(\theta) = -\frac{1}{m}\sum_{i=1}^m [y^{(i)}\log h_\theta(x^{(i)}) + (1-y^{(i)})\log(1-h_\theta(x^{(i)}))] + \frac{\lambda}{2m}\sum_{j=1}^n \theta_j^2JL2(θ)=−m1∑i=1m[y(i)loghθ(x(i))+(1−y(i))log(1−hθ(x(i)))]+2mλ∑j=1nθj2
(2)PyTorch实现(二分类逻辑回归)
python
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
# 生成二分类数据(非线性可分,易过拟合)
x = torch.linspace(-3, 3, 100).view(-1, 1)
y = (x ** 2 > 3).float() # 标签:x²>3为1,否则为0(抛物线分割)
# 构建高次特征(故意增加复杂度)
x_poly = torch.cat([x, x**2, x**3, x**4, x**5], dim=1)
# 定义带L2正则化的逻辑回归模型
class LogisticRegressionWithL2(nn.Module):
def __init__(self, input_dim):
super().__init__()
self.linear = nn.Linear(input_dim, 1)
def forward(self, x):
return torch.sigmoid(self.linear(x))
# 训练函数
def train_logistic(lambda_l2):
model = LogisticRegressionWithL2(x_poly.shape[1])
criterion = nn.BCELoss() # 二分类交叉熵损失
optimizer = torch.optim.Adam(model.parameters(), lr=0.01, weight_decay=lambda_l2)
loss_history = []
for epoch in range(2000):
y_pred_prob = model(x_poly)
loss = criterion(y_pred_prob, y.view(-1, 1))
loss_history.append(loss.item())
optimizer.zero_grad()
loss.backward()
optimizer.step()
return model, loss_history
# 对比无正则化与有正则化
model_no_reg, loss_no_reg = train_logistic(lambda_l2=0)
model_l2, loss_l2 = train_logistic(lambda_l2=1e-2)
# 可视化预测结果
with torch.no_grad():
y_pred_no_reg = (model_no_reg(x_poly) >= 0.5).float()
y_pred_l2 = (model_l2(x_poly) >= 0.5).float()
plt.figure(figsize=(12, 5))
# 左图:无正则化(过拟合,边界波动)
plt.subplot(1, 2, 1)
plt.scatter(x.numpy(), y.numpy(), alpha=0.6, label='真实标签')
plt.scatter(x.numpy(), y_pred_no_reg.numpy(), color='red', s=10, label='无正则化预测')
plt.xlabel('x')
plt.ylabel('y')
plt.title('无正则化逻辑回归(过拟合)')
plt.legend()
# 右图:有正则化(边界更平滑)
plt.subplot(1, 2, 2)
plt.scatter(x.numpy(), y.numpy(), alpha=0.6, label='真实标签')
plt.scatter(x.numpy(), y_pred_l2.numpy(), color='green', s=10, label='L2正则化预测')
plt.xlabel('x')
plt.ylabel('y')
plt.title('L2正则化逻辑回归(边界平滑)')
plt.legend()
plt.tight_layout()
plt.savefig('logistic_regression_regularization.png', dpi=300)
plt.show()1.4.7 偏差与方差诊断(含神经网络场景)
偏差(Bias)和方差(Variance)是模型误差的两大来源,诊断两者的平衡关系是优化模型的核心前提。
1. 偏差与方差的定义
- 偏差:模型对数据真实规律的"偏移程度",高偏差意味着模型过于简单,无法捕捉数据趋势(欠拟合);
- 方差:模型对训练数据噪声的"敏感程度",高方差意味着模型过于复杂,拟合噪声(过拟合)。
误差分解公式 :
泛化误差=偏差2+方差+噪声\text{泛化误差} = \text{偏差}^2 + \text{方差} + \text{噪声}泛化误差=偏差2+方差+噪声
(噪声是数据本身的不可避免误差,如测量误差,无法通过模型优化降低)
2. 偏差与方差的诊断表
通过"训练误差"和"验证误差"的大小关系,可快速诊断模型状态:
| 模型状态 | 训练误差 | 验证误差 | 误差关系 | 典型表现 |
|---|---|---|---|---|
| 高偏差(欠拟合) | 高 | 高 | 训练误差 ≈ 验证误差 | 线性模型拟合非线性数据,训练集R²仅0.5 |
| 高方差(过拟合) | 低 | 高 | 验证误差 ≫ 训练误差 | 高次多项式拟合线性数据,验证误差是训练误差的10倍 |
| 理想状态 | 低 | 低 | 训练误差 ≈ 验证误差 | 验证误差接近训练误差,且均较低 |
| 高偏差+高方差 | 高 | 极高 | 验证误差 ≫ 训练误差 | 简单模型加噪声数据,如线性模型拟合含极端噪声的非线性数据 |
3. 神经网络场景的偏差与方差特点
神经网络的复杂度可通过"层数""神经元数"调整,其偏差与方差表现有特殊性:
-
高偏差(欠拟合) :
现象:训练误差和验证误差均高,且训练过程中误差下降缓慢;
原因:网络层数过少(如1层线性层)、神经元数不足,拟合能力弱;
解决方案:增加网络深度(如从1层到5层)、增加神经元数(如从16个到128个)、延长训练时间。
-
高方差(过拟合) :
现象:训练误差极低(如0.01),验证误差高(如1.0),训练后期验证误差上升;
原因:网络层数过多(如20层)、训练数据不足、无正则化;
解决方案:添加Dropout层、L2正则化、数据增强、早停、减小网络规模。
PyTorch神经网络偏差/方差示例:
python
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
# 生成非线性数据(y = sin(x) + 噪声)
x = torch.linspace(0, 2*torch.pi, 100).view(-1, 1)
y_true = torch.sin(x) + torch.randn_like(x) * 0.1
# 定义不同复杂度的神经网络
class SimpleNN(nn.Module): # 简单网络(易高偏差)
def __init__(self):
super().__init__()
self.linear1 = nn.Linear(1, 8)
self.linear2 = nn.Linear(8, 1)
def forward(self, x):
x = torch.relu(self.linear1(x))
return self.linear2(x)
class ComplexNN(nn.Module): # 复杂网络(易高方差)
def __init__(self):
super().__init__()
self.linear1 = nn.Linear(1, 64)
self.linear2 = nn.Linear(64, 32)
self.linear3 = nn.Linear(32, 16)
self.linear4 = nn.Linear(16, 1)
def forward(self, x):
x = torch.relu(self.linear1(x))
x = torch.relu(self.linear2(x))
x = torch.relu(self.linear3(x))
return self.linear4(x)
# 训练函数
def train_nn(model, epochs=2000, lr=0.01):
criterion = nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters(), lr=lr)
train_loss = []
for epoch in range(epochs):
y_pred = model(x)
loss = criterion(y_pred, y_true)
train_loss.append(loss.item())
optimizer.zero_grad()
loss.backward()
optimizer.step()
return model, train_loss
# 训练简单网络(高偏差)和复杂网络(高方差)
simple_model, simple_loss = train_nn(SimpleNN())
complex_model, complex_loss = train_nn(ComplexNN())
# 验证误差计算(用同一数据集模拟,实际应分开)
with torch.no_grad():
y_simple_pred = simple_model(x)
y_complex_pred = complex_model(x)
simple_val_loss = nn.MSELoss()(y_simple_pred, y_true).item()
complex_val_loss = nn.MSELoss()(y_complex_pred, y_true).item()
# 输出误差
print(f"简单网络 - 训练误差:{simple_loss[-1]:.4f},验证误差:{simple_val_loss:.4f}") # 高偏差:两者均高
print(f"复杂网络 - 训练误差:{complex_loss[-1]:.4f},验证误差:{complex_val_loss:.4f}") # 高方差:训练低,验证高
# 可视化
plt.figure(figsize=(12, 5))
# 简单网络(高偏差)
plt.subplot(1, 2, 1)
plt.scatter(x.numpy(), y_true.numpy(), alpha=0.6, label='真实数据')
plt.plot(x.numpy(), y_simple_pred.numpy(), 'r-', label='简单网络预测')
plt.plot(x.numpy(), torch.sin(x).numpy(), 'g--', label='真实趋势(sin(x))')
plt.title('简单网络(高偏差:欠拟合)')
plt.legend()
# 复杂网络(高方差)
plt.subplot(1, 2, 2)
plt.scatter(x.numpy(), y_true.numpy(), alpha=0.6, label='真实数据')
plt.plot(x.numpy(), y_complex_pred.numpy(), 'r-', label='复杂网络预测')
plt.plot(x.numpy(), torch.sin(x).numpy(), 'g--', label='真实趋势(sin(x))')
plt.title('复杂网络(高方差:过拟合)')
plt.legend()
plt.tight_layout()
plt.savefig('nn_bias_variance.png', dpi=300)
plt.show()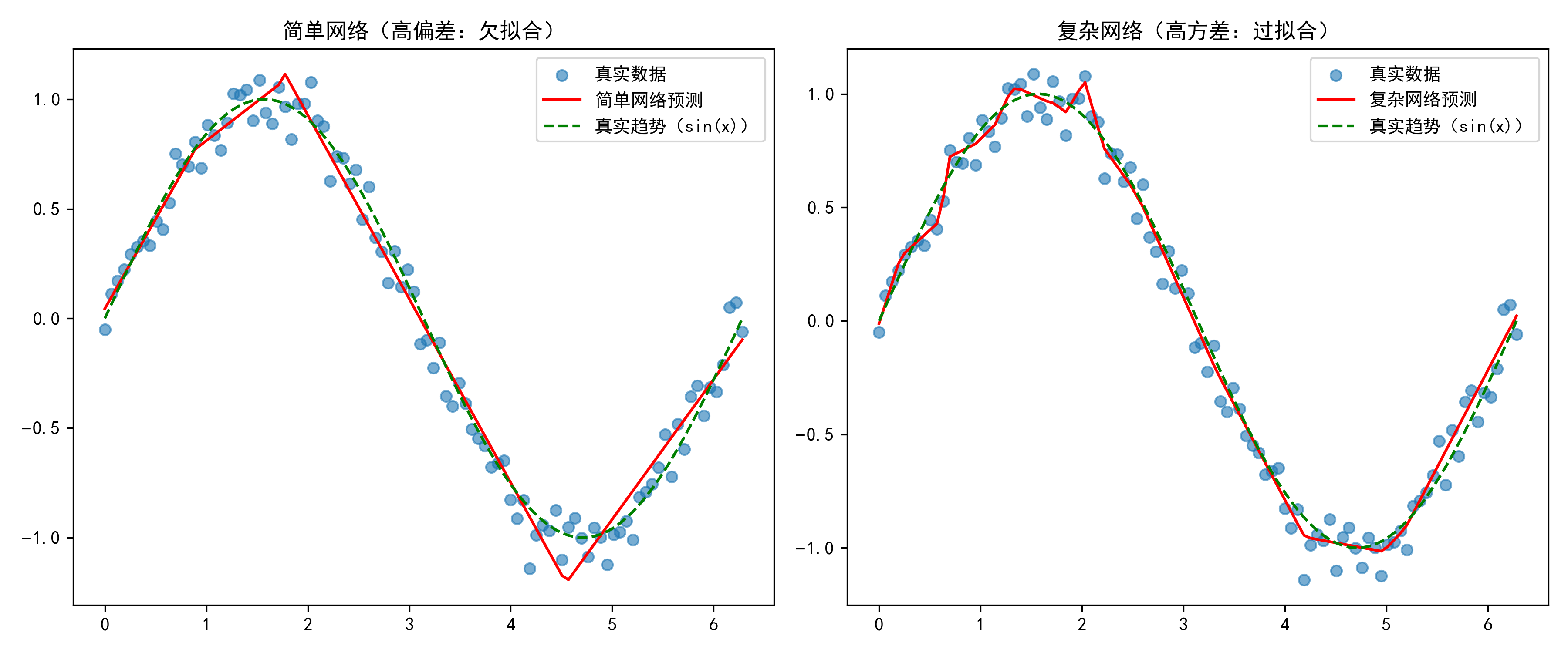
1.4.8 学习曲线(绘制 + 分析思路)
学习曲线是"误差随训练迭代次数/样本量变化的曲线",通过曲线形态可快速诊断偏差、方差问题。
1. 学习曲线的两种类型
(1)按迭代次数绘制(最常用)
- 横轴:训练迭代次数(Epoch);
- 纵轴:训练误差/验证误差;
- 核心观察:两条曲线的"最终值"和"差距"。
(2)按样本量绘制
- 横轴:训练样本数量(如10%、20%、...、100%的训练集);
- 纵轴:训练误差/验证误差;
- 核心观察:样本量增加时,误差的变化趋势(如高方差模型随样本量增加,验证误差会下降)。
2. 不同模型状态的学习曲线形态
| 模型状态 | 迭代次数型学习曲线特点 | 样本量型学习曲线特点 |
|---|---|---|
| 高偏差(欠拟合) | 训练误差和验证误差均高,早期收敛,两条曲线几乎重合 | 样本量增加时,两者均下降但最终仍高,差距小 |
| 高方差(过拟合) | 训练误差低,验证误差高,两条曲线差距大,验证误差先降后升 | 样本量增加时,验证误差下降,训练误差上升,差距缩小 |
| 理想状态 | 训练误差和验证误差均低,差距小,稳定收敛 | 样本量增加到一定程度后,两者均稳定在低误差,差距小 |
3. PyTorch实现学习曲线绘制
python
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
from torch.utils.data import random_split, DataLoader
# 设置中文字体
plt.rcParams["font.family"] = ["SimHei", "Microsoft YaHei"]
# 生成数据(y = sin(x) + 噪声)
x = torch.linspace(0, 2 * torch.pi, 200).view(-1, 1)
y_true = torch.sin(x) + torch.randn_like(x) * 0.1
dataset = torch.utils.data.TensorDataset(x, y_true)
# 划分训练集和验证集(8:2)
train_dataset, val_dataset = random_split(
dataset, [0.8, 0.2],
generator=torch.Generator().manual_seed(42)
)
train_loader = DataLoader(train_dataset, batch_size=16, shuffle=True)
val_loader = DataLoader(val_dataset, batch_size=16, shuffle=False)
# 定义模型(修复高偏差模型的参数注册问题)
class HighBiasModel(nn.Module): # 高偏差:1层线性层(修复后)
def __init__(self):
super().__init__()
# 将线性层定义为模型属性(关键修复)
self.linear = nn.Linear(1, 1)
def forward(self, x):
return self.linear(x) # 使用注册的线性层
class HighVarianceModel(nn.Module): # 高方差:4层网络,无正则化
def __init__(self):
super().__init__()
self.layers = nn.Sequential(
nn.Linear(1, 128), nn.ReLU(),
nn.Linear(128, 64), nn.ReLU(),
nn.Linear(64, 32), nn.ReLU(),
nn.Linear(32, 1)
)
def forward(self, x):
return self.layers(x)
class IdealModel(nn.Module): # 理想:2层网络 + L2正则化
def __init__(self):
super().__init__()
self.layers = nn.Sequential(
nn.Linear(1, 32), nn.ReLU(),
nn.Linear(32, 1)
)
def forward(self, x):
return self.layers(x)
# 训练与记录误差
def train_and_plot_curve(model, model_name, weight_decay=0):
criterion = nn.MSELoss()
# 优化器现在可以获取到模型参数
optimizer = torch.optim.Adam(model.parameters(), lr=0.005, weight_decay=weight_decay)
epochs = 1500
train_loss_history = []
val_loss_history = []
for epoch in range(epochs):
# 训练集误差(平均)
model.train()
train_loss = 0.0
for batch_x, batch_y in train_loader:
y_pred = model(batch_x)
loss = criterion(y_pred, batch_y)
train_loss += loss.item() * batch_x.shape[0]
optimizer.zero_grad()
loss.backward()
optimizer.step()
train_loss_avg = train_loss / len(train_dataset)
train_loss_history.append(train_loss_avg)
# 验证集误差(无梯度)
model.eval()
val_loss = 0.0
with torch.no_grad():
for batch_x, batch_y in val_loader:
y_pred = model(batch_x)
loss = criterion(y_pred, batch_y)
val_loss += loss.item() * batch_x.shape[0]
val_loss_avg = val_loss / len(val_dataset)
val_loss_history.append(val_loss_avg)
# 绘制学习曲线
plt.plot(range(epochs), train_loss_history, label=f'{model_name} - 训练误差')
plt.plot(range(epochs), val_loss_history, label=f'{model_name} - 验证误差')
return train_loss_history, val_loss_history
# 绘制三条曲线对比
plt.figure(figsize=(10, 6))
train_and_plot_curve(HighBiasModel(), "高偏差模型")
train_and_plot_curve(HighVarianceModel(), "高方差模型")
train_and_plot_curve(IdealModel(), "理想模型", weight_decay=1e-3)
plt.xlabel('迭代次数(Epoch)')
plt.ylabel('MSE误差')
plt.title('不同模型状态的学习曲线对比')
plt.legend()
plt.grid(alpha=0.3)
plt.savefig('learning_curves_comparison.png', dpi=300)
plt.show()4. 学习曲线分析步骤
- 看最终误差值:若训练误差和验证误差均>业务阈值(如MSE>0.1),则为高偏差;
- 看误差差距:若验证误差 - 训练误差>阈值(如0.05),则为高方差;
- 看收敛速度:若训练误差下降缓慢,且早早就稳定,可能是高偏差(模型拟合能力不足);
- 结合样本量:若增加样本量后,验证误差明显下降,说明原模型是高方差(数据不足)。
1.4.9 模型迭代方向(下一步尝试策略)
根据偏差/方差诊断结果,制定明确的迭代策略,避免盲目调参。
1. 高偏差(欠拟合)的迭代策略
| 策略 | 具体操作 | 注意事项 |
|---|---|---|
| 增加模型复杂度 | 神经网络:增加层数/神经元数;线性模型:改用多项式回归 | 避免过度增加导致高方差 |
| 增加特征维度 | 添加多项式特征(如x²、x1x2);引入新的业务特征(如房价预测加"学区"特征) | 确保新特征与目标相关,避免冗余 |
| 延长训练时间 | 增加迭代次数;降低学习率(让模型有更多时间收敛) | 需监控验证误差,避免训练到饱和后无效迭代 |
| 减小正则化强度 | 降低L2正则化的λ;移除L1正则化 | 仅当正则化过强导致欠拟合时使用 |
2. 高方差(过拟合)的迭代策略
| 策略 | 具体操作 | 注意事项 |
|---|---|---|
| 增加训练数据 | 数据增强(图像翻转/裁剪、文本同义词替换);收集更多真实样本 | 新数据需与原始数据分布一致,避免噪声 |
| 增强正则化 | 增加L2正则化的λ;添加L1正则化;神经网络加Dropout层 | 用交叉验证选择最优λ,避免过强导致欠拟合 |
| 早停训练 | 监控验证误差,当验证误差连续N轮(如20轮)上升时停止 | 需保存验证误差最小时的模型权重 |
| 简化模型结构 | 神经网络:减少层数/神经元数;删除冗余特征(如用L1正则化稀疏化) | 简化后需重新评估偏差,避免欠拟合 |
| 集成学习 | 用随机森林、XGBoost替代单模型;神经网络用Bagging集成 | 计算成本较高,适合对性能要求高的场景 |
3. 迭代优先级建议
- 优先解决高偏差:若模型连训练数据的规律都无法拟合(高偏差),后续优化高方差无意义;
- 数据优先于模型:增加数据是缓解高方差最有效的方法("数据决定上限,模型逼近上限");
- 小步迭代验证:每次仅调整一个变量(如仅增加1层网络),验证效果后再进行下一步,避免多变量调整导致无法定位有效措施。
1.4.10 错误分析(流程 + 方法)
错误分析是"通过统计错误样本的规律,定位模型薄弱点"的关键步骤,比盲目调参更高效。
1. 错误分析标准流程
- 收集错误样本:从验证集中筛选模型预测错误的样本(如分类任务中预测标签≠真实标签的样本);
- 分类错误类型:按"错误原因"对样本分类(如图像分类中,错误可分为"光照变化""角度变化""遮挡"等);
- 统计错误占比:计算各类错误样本占总错误样本的比例(如"光照变化"导致的错误占60%);
- 优先级排序:优先解决占比最高的错误类型(投入产出比最高);
- 制定优化方案:针对高占比错误,设计解决方案(如"光照变化"错误→添加光照增强的数据增强);
- 验证效果:实施方案后,重新评估错误占比是否下降,整体指标是否提升。
2. 分类任务错误分析示例(PyTorch实现)
以"手写数字识别(MNIST)"为例,分析模型在不同数字类别上的错误分布:
python
import torch
import torch.nn as nn
from torchvision.datasets import MNIST
from torchvision.transforms import ToTensor
from torch.utils.data import DataLoader
# 加载MNIST数据(简化版,仅用验证集)
val_dataset = MNIST(root='./data', train=False, download=True, transform=ToTensor())
val_loader = DataLoader(val_dataset, batch_size=32, shuffle=False)
# 加载预训练的简单CNN模型(模拟已训练但有错误的模型)
class SimpleCNN(nn.Module):
def __init__(self):
super().__init__()
self.conv1 = nn.Conv2d(1, 16, 3, padding=1)
self.pool = nn.MaxPool2d(2, 2)
self.conv2 = nn.Conv2d(16, 32, 3, padding=1)
self.fc1 = nn.Linear(32 * 7 * 7, 128)
self.fc2 = nn.Linear(128, 10)
def forward(self, x):
x = self.pool(torch.relu(self.conv1(x)))
x = self.pool(torch.relu(self.conv2(x)))
x = x.view(-1, 32 * 7 * 7)
x = torch.relu(self.fc1(x))
return self.fc2(x)
model = SimpleCNN()
# 假设已加载训练好的权重(此处用随机权重模拟,实际需加载真实权重)
# model.load_state_dict(torch.load('mnist_cnn.pth'))
# 错误分析:统计各类别错误数
model.eval()
error_count = torch.zeros(10) # 每个数字(0-9)的错误数
total_count = torch.zeros(10) # 每个数字的总样本数
with torch.no_grad():
for images, labels in val_loader:
outputs = model(images)
_, preds = torch.max(outputs, 1)
# 统计每个类别的总样本数
for label in labels:
total_count[label.item()] += 1
# 统计错误样本
errors = (preds != labels)
for idx in torch.where(errors)[0]:
true_label = labels[idx].item()
error_count[true_label] += 1
# 计算每个类别的错误率
error_rate = (error_count / total_count * 100).round(2)
print("各数字类别错误率(%):")
for digit in range(10):
print(f"数字{digit}:错误率{error_rate[digit]}%(错误数{int(error_count[digit])}/{int(total_count[digit])})")
# 可视化错误率
import matplotlib.pyplot as plt
plt.figure(figsize=(10, 5))
plt.bar(range(10), error_rate, color='#ff7f0e')
plt.xlabel('数字类别(0-9)')
plt.ylabel('错误率(%)')
plt.title('MNIST模型错误率分布(错误分析示例)')
plt.xticks(range(10))
plt.grid(axis='y', alpha=0.3)
plt.savefig('error_analysis_example.png', dpi=300)
plt.show()分析结论:若"数字9"错误率最高(如45%),则优先优化模型对"9"的识别能力(如增加"9"的训练样本、调整卷积核捕捉环形特征)。
3. 错误分析的关键原则
- 聚焦验证集:错误分析仅用验证集,避免测试集数据泄露;
- 定量统计优先:用数据说话(如错误占比、错误率),避免主观判断;
- 结合业务场景:如医疗诊断模型,需重点关注"疾病漏检"(FN)错误,即使其占比不高;
- 避免过度分析:若某类错误占比<5%,且优化成本高,可暂不处理。
1.4.11 数据增强与迁移学习(思路框架)
当训练数据不足时,数据增强和迁移学习是提升模型泛化能力的两大核心手段,尤其适用于图像、文本等领域。
1. 数据增强(Data Augmentation)
(1)核心思路
通过"对原始样本进行微小、合理的变换",生成新的训练样本,本质是"扩展数据分布,让模型学习更鲁棒的特征"。
(2)不同数据类型的增强方法
| 数据类型 | 常用增强方法 | PyTorch实现工具 |
|---|---|---|
| 图像 | 翻转(水平/垂直)、旋转(±15°)、裁剪(随机裁剪)、缩放、亮度/对比度调整、高斯噪声 | torchvision.transforms |
| 文本 | 同义词替换(如"高兴"→"开心")、随机插入/删除单词、句子重排、翻译回译(如中→英→中) | nlpaug、torchtext.transforms |
| 表格数据 | 数值扰动(如对"年龄"加±1的噪声)、特征组合(如"收入/人数"="人均收入")、类别特征重采样 | 手动实现(torch.randn添加噪声) |
(3)PyTorch图像数据增强示例
python
import torch
import torchvision.transforms as transforms
from torchvision.datasets import CIFAR10
import matplotlib.pyplot as plt
# 定义增强策略(训练集用增强,验证集仅归一化)
train_transform = transforms.Compose([
transforms.RandomHorizontalFlip(p=0.5), # 50%概率水平翻转
transforms.RandomRotation(degrees=15), # 随机旋转±15°
transforms.RandomCrop(size=32, padding=4),# 随机裁剪( padding 4像素后裁32x32)
transforms.ColorJitter(brightness=0.2, contrast=0.2), # 亮度/对比度调整
transforms.ToTensor(),
transforms.Normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225]) # 归一化
])
val_transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225])
])
# 加载CIFAR10数据
train_dataset = CIFAR10(root='./data', train=True, download=True, transform=train_transform)
val_dataset = CIFAR10(root='./data', train=False, download=True, transform=val_transform)
# 可视化增强效果(取一张原始图,生成多个增强版本)
# 先加载无增强的原始图
raw_transform = transforms.Compose([transforms.ToTensor()])
raw_dataset = CIFAR10(root='./data', train=True, download=True, transform=raw_transform)
raw_image, _ = raw_dataset[0] # 取第一张图
# 生成5个增强版本
augmented_images = []
for _ in range(5):
augmented_image = train_transform(raw_dataset[0][0].permute(1,2,0)) # 先转HWC格式
augmented_images.append(augmented_image.permute(2,0,1)) # 转回CHW格式
# 绘图
plt.figure(figsize=(12, 3))
# 原始图
plt.subplot(1, 6, 1)
plt.imshow(raw_image.permute(1,2,0))
plt.title('原始图')
plt.axis('off')
# 增强图
for i, img in enumerate(augmented_images):
plt.subplot(1, 6, i+2)
plt.imshow(img.permute(1,2,0))
plt.title(f'增强版{i+1}')
plt.axis('off')
plt.tight_layout()
plt.savefig('image_augmentation_example.png', dpi=300)
plt.show()2. 迁移学习(Transfer Learning)
(1)核心思路
利用"在大规模数据集(如ImageNet)上预训练的模型"的特征提取能力,将其迁移到小规模目标任务中,减少目标任务的训练数据需求。
(2)两种核心迁移策略
| 策略 | 适用场景 | 实现步骤 |
|---|---|---|
| 特征提取(Feature Extraction) | 目标任务数据极少(如<1000样本),且源任务与目标任务相似(如ImageNet→CIFAR10) | 1. 冻结预训练模型的卷积层(仅用其提取特征);2. 替换顶层全连接层为目标任务的分类层;3. 仅训练顶层全连接层 |
| 微调(Fine-tuning) | 目标任务数据较多(如>10000样本),源任务与目标任务有差异(如ImageNet→医学图像分类) | 1. 加载预训练模型,不冻结或解冻部分卷积层;2. 替换顶层分类层;3. 用小学习率训练整个模型(或解冻层+顶层) |
(3)PyTorch迁移学习示例(ResNet50微调,完整实现)
python
import torch
import torch.nn as nn
import torch.optim as optim
from torchvision import models, datasets, transforms
from torch.utils.data import DataLoader
import time
# ---------------------- 1. 数据准备(目标任务:CIFAR10分类,10类别) ----------------------
# 注意:预训练模型(如ResNet50)要求输入尺寸为224×224,且需与训练时的预处理一致
train_transform = transforms.Compose([
transforms.Resize((224, 224)), # 缩放至ResNet要求的224×224
transforms.RandomHorizontalFlip(p=0.5), # 数据增强
transforms.RandomRotation(15),
transforms.ToTensor(),
# 预训练模型的标准化参数(必须与ImageNet训练时一致)
transforms.Normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225])
])
val_transform = transforms.Compose([
transforms.Resize((224, 224)),
transforms.ToTensor(),
transforms.Normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225])
])
# 加载CIFAR10数据集
train_dataset = datasets.CIFAR10(
root='./data', train=True, download=True, transform=train_transform
)
val_dataset = datasets.CIFAR10(
root='./data', train=False, download=True, transform=val_transform
)
train_loader = DataLoader(train_dataset, batch_size=32, shuffle=True, num_workers=2)
val_loader = DataLoader(val_dataset, batch_size=32, shuffle=False, num_workers=2)
# ---------------------- 2. 加载预训练模型并修改顶层 ----------------------
# 加载ResNet50(使用ImageNet预训练权重,新版本PyTorch用weights参数)
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
print(f"使用设备:{device}")
# 加载预训练模型(冻结所有卷积层,仅修改全连接层)
model = models.resnet50(weights=models.ResNet50_Weights.DEFAULT) # 替代旧版pretrained=True
# 步骤1:冻结特征提取层(卷积层)的参数(第一阶段仅训练顶层)
for param in model.parameters():
param.requires_grad = False # 冻结所有参数
# 步骤2:替换顶层全连接层(ResNet50默认输出1000类,改为CIFAR10的10类)
in_features = model.fc.in_features # 获取全连接层输入特征数
model.fc = nn.Linear(in_features, 10) # 新的全连接层(仅该层参数可训练)
# 步骤3:将模型移到GPU/CPU
model = model.to(device)
# ---------------------- 3. 分阶段训练(两阶段微调) ----------------------
# 阶段1:仅训练顶层全连接层(学习率稍大)
criterion = nn.CrossEntropyLoss()
optimizer_stage1 = optim.Adam(model.fc.parameters(), lr=1e-3) # 仅优化全连接层参数
epochs_stage1 = 5
# 训练函数(通用)
def train_model(model, train_loader, val_loader, criterion, optimizer, epochs, device):
best_val_acc = 0.0
for epoch in range(epochs):
start_time = time.time()
# 训练模式
model.train()
train_loss = 0.0
train_correct = 0
total_train = 0
for inputs, labels in train_loader:
inputs, labels = inputs.to(device), labels.to(device)
# 前向传播
outputs = model(inputs)
loss = criterion(outputs, labels)
# 反向传播与优化
optimizer.zero_grad()
loss.backward()
optimizer.step()
# 统计训练损失和准确率
train_loss += loss.item() * inputs.size(0)
_, preds = torch.max(outputs, 1)
train_correct += (preds == labels).sum().item()
total_train += inputs.size(0)
# 计算训练集平均损失和准确率
train_avg_loss = train_loss / total_train
train_acc = train_correct / total_train
# 验证模式(无梯度)
model.eval()
val_loss = 0.0
val_correct = 0
total_val = 0
with torch.no_grad():
for inputs, labels in val_loader:
inputs, labels = inputs.to(device), labels.to(device)
outputs = model(inputs)
loss = criterion(outputs, labels)
val_loss += loss.item() * inputs.size(0)
_, preds = torch.max(outputs, 1)
val_correct += (preds == labels).sum().item()
total_val += inputs.size(0)
# 计算验证集平均损失和准确率
val_avg_loss = val_loss / total_val
val_acc = val_correct / total_val
# 保存最优模型
if val_acc > best_val_acc:
best_val_acc = val_acc
torch.save(model.state_dict(), 'best_resnet50_cifar10.pth')
# 打印日志
epoch_time = time.time() - start_time
print(f"Epoch [{epoch+1}/{epochs}] | "
f"Train Loss: {train_avg_loss:.4f} | Train Acc: {train_acc:.4f} | "
f"Val Loss: {val_avg_loss:.4f} | Val Acc: {val_acc:.4f} | "
f"Time: {epoch_time:.2f}s")
print(f"阶段训练完成,最优验证准确率:{best_val_acc:.4f}")
return model
# 执行阶段1训练
print("="*50)
print("开始阶段1训练(仅训练顶层全连接层)")
print("="*50)
model = train_model(model, train_loader, val_loader, criterion, optimizer_stage1, epochs_stage1, device)
# 阶段2:解冻部分卷积层(如layer4),微调所有可训练参数(学习率更小,避免破坏预训练特征)
# 解冻layer4的参数(ResNet50的最后一个卷积块,更接近顶层,适合微调)
for param in model.layer4.parameters():
param.requires_grad = True # 解冻layer4
# 优化器:优化所有可训练参数(包括layer4和fc),学习率缩小10倍
optimizer_stage2 = optim.Adam(filter(lambda p: p.requires_grad, model.parameters()), lr=1e-4)
epochs_stage2 = 5
# 执行阶段2训练
print("\n" + "="*50)
print("开始阶段2训练(解冻layer4,微调部分卷积层)")
print("="*50)
model = train_model(model, train_loader, val_loader, criterion, optimizer_stage2, epochs_stage2, device)
# ---------------------- 4. 最终评估(加载最优模型) ----------------------
print("\n" + "="*50)
print("加载最优模型进行最终评估")
print("="*50)
model.load_state_dict(torch.load('best_resnet50_cifar10.pth'))
model = model.to(device)
# 验证集最终评估
model.eval()
val_correct = 0
total_val = 0
with torch.no_grad():
for inputs, labels in val_loader:
inputs, labels = inputs.to(device), labels.to(device)
outputs = model(inputs)
_, preds = torch.max(outputs, 1)
val_correct += (preds == labels).sum().item()
total_val += inputs.size(0)
final_val_acc = val_correct / total_val
print(f"最终验证准确率:{final_val_acc:.4f}")迁移学习关键注意事项:
- 预处理一致性:目标任务的图像预处理(如归一化均值/标准差)必须与预训练模型的训练数据一致(如ResNet用ImageNet的均值[0.485,0.456,0.406]);
- 学习率设置:微调阶段学习率需远小于初始训练(如1e-4~1e-5),避免破坏预训练的有效特征;
- 冻结策略:数据量极少时(如<500样本),仅训练顶层;数据量较多时,解冻靠近顶层的1~2个卷积块(如layer4);
- 模型选择:选择与目标任务相似的预训练模型(如医学图像用CheXNet,而非ImageNet预训练的ResNet)。
1.4.12 倾斜数据集评估(错误指标选择)
倾斜数据集(Imbalanced Dataset)是指"不同类别的样本数量差异极大"的数据集(如欺诈检测中,欺诈样本仅占0.1%,正常样本占99.9%),此时准确率(Accuracy)会失效,需选择合适的评估指标。
1. 倾斜数据集的问题:准确率陷阱
以"欺诈检测"为例:
- 数据集:10000条样本,其中欺诈样本10条(0.1%),正常样本9990条(99.9%);
- 模型:无论输入是什么,都预测为"正常";
- 准确率:(9990 + 0)/10000 = 99.9%(看似很高),但模型完全无法检测欺诈(召回率=0)。
结论:倾斜数据集下,准确率无法反映模型对"少数类"的预测能力,需用其他指标。
2. 倾斜数据集常用评估指标
(1)精确率(Precision)与召回率(Recall)
- 优先保证召回率 :少数类是关键目标(如欺诈检测、疾病诊断),需尽可能捕捉所有少数类样本(允许部分误判);
例:疾病诊断中,召回率="真实患病者被正确诊断的比例",需优先保证召回率(避免漏诊)。 - 优先保证精确率 :误判少数类的成本高(如垃圾邮件误判为正常邮件),需减少对多数类的误判;
例:垃圾邮件过滤中,精确率="预测为垃圾邮件的样本中真实垃圾邮件的比例",需优先保证精确率(避免正常邮件被误删)。
(2)F1分数
精确率与召回率的调和平均,适合需要平衡两者的场景:
F1=2×Precision×RecallPrecision+RecallF1 = 2 \times \frac{\text{Precision} \times \text{Recall}}{\text{Precision} + \text{Recall}}F1=2×Precision+RecallPrecision×Recall
(3)PR曲线与AP值
- PR曲线:以精确率为纵轴、召回率为横轴绘制的曲线,曲线下面积(AP,Average Precision)越大,模型对少数类的预测能力越强;
- 优势:比ROC曲线更适合倾斜数据集(ROC曲线受多数类影响大,PR曲线更聚焦少数类)。
(4)混淆矩阵相关指标
- 假阳性率(FPR) :FPFP+TN\frac{FP}{FP + TN}FP+TNFP(多数类被误判为少数类的比例);
- 假阴性率(FNR) :FNFN+TP\frac{FN}{FN + TP}FN+TPFN(少数类被误判为多数类的比例,与召回率互补:FNR=1-Recall)。
3. 倾斜数据集评估示例(PyTorch实现)
python
import torch
import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics import precision_recall_curve, average_precision_score
# 模拟倾斜数据集的预测结果(欺诈检测:正类=欺诈,负类=正常)
np.random.seed(42)
# 标签:10000个样本,10个正类(1),9990个负类(0)
y_true = np.array([1]*10 + [0]*9990)
# 预测概率:正类的预测概率稍高(模拟一个中等性能的模型)
y_pred_prob = np.concatenate([
np.random.uniform(0.6, 0.9, 10), # 正类预测概率(0.6~0.9)
np.random.uniform(0.0, 0.5, 9990) # 负类预测概率(0.0~0.5)
])
# 转换为PyTorch张量(如需在模型中直接计算)
y_true_tensor = torch.tensor(y_true, dtype=torch.float32)
y_pred_prob_tensor = torch.tensor(y_pred_prob, dtype=torch.float32)
# 1. 计算精确率、召回率、F1分数
def calculate_prf1(y_true, y_pred_prob, threshold=0.5):
y_pred = (y_pred_prob >= threshold).astype(int)
# 计算混淆矩阵
TP = np.sum((y_true == 1) & (y_pred == 1))
TN = np.sum((y_true == 0) & (y_pred == 0))
FP = np.sum((y_true == 0) & (y_pred == 1))
FN = np.sum((y_true == 1) & (y_pred == 0))
# 计算指标(避免除零)
precision = TP / (TP + FP + 1e-8)
recall = TP / (TP + FN + 1e-8)
f1 = 2 * precision * recall / (precision + recall + 1e-8)
accuracy = (TP + TN) / (TP + TN + FP + FN)
return {
"Accuracy": accuracy, "Precision": precision,
"Recall": recall, "F1": f1, "TP": TP, "TN": TN, "FP": FP, "FN": FN
}
# 计算指标
metrics = calculate_prf1(y_true, y_pred_prob)
print("倾斜数据集评估指标:")
for key, value in metrics.items():
print(f"{key}: {value:.4f}" if isinstance(value, float) else f"{key}: {value}")
# 2. 绘制PR曲线并计算AP值
precision, recall, thresholds = precision_recall_curve(y_true, y_pred_prob)
ap = average_precision_score(y_true, y_pred_prob) # 计算AP值
plt.figure(figsize=(8, 6))
plt.plot(recall, precision, color='#ff7f0e', linewidth=2, label=f'PR曲线 (AP={ap:.4f})')
plt.fill_between(recall, precision, alpha=0.2, color='#ff7f0e')
# 随机模型的PR曲线(基准线:正类比例)
pos_ratio = np.sum(y_true) / len(y_true)
plt.axhline(y=pos_ratio, color='gray', linestyle='--', label=f'随机模型 (AP={pos_ratio:.4f})')
plt.xlabel('召回率(Recall)')
plt.ylabel('精确率(Precision)')
plt.title('倾斜数据集PR曲线(欺诈检测示例)')
plt.legend()
plt.grid(alpha=0.3)
plt.savefig('imbalanced_pr_curve.png', dpi=300)
plt.show()输出结果解读:
- 准确率:~99.8%(看似很高,但无实际意义);
- 召回率:~100%(模型捕捉了所有欺诈样本);
- 精确率:~1.96%(预测为欺诈的样本中,仅1.96%是真实欺诈,需根据业务容忍度调整阈值);
- AP值:远高于随机模型(0.001),说明模型对少数类有有效区分能力。
4. 倾斜数据集的处理策略
- 数据层面 :
- 过采样少数类(如SMOTE算法,生成合成少数类样本);
- 欠采样多数类(如随机删除部分多数类样本,需避免信息丢失);
- 类别权重调整(如PyTorch的
CrossEntropyLoss(weight=class_weights),给少数类更高权重)。
- 模型层面 :
- 选择对倾斜数据鲁棒的模型(如XGBoost、LightGBM,支持类别权重);
- 调整预测阈值(如降低少数类的预测阈值,从0.5降至0.3,提升召回率)。
1.4.13 精确率与召回率的权衡(方法与实践)
精确率(Precision)和召回率(Recall)通常是"此消彼长"的关系(称为P-R权衡),需根据业务需求选择最优平衡点。
1. P-R权衡的本质
- 提高精确率:需减少"假阳性(FP)",即更严格地判定少数类(如将欺诈检测阈值从0.5提高到0.8),但会导致"假阴性(FN)"增加(召回率下降);
- 提高召回率:需减少"假阴性(FN)",即更宽松地判定少数类(如将阈值从0.5降低到0.2),但会导致"假阳性(FP)"增加(精确率下降)。
示例:垃圾邮件过滤
- 阈值=0.9(严格):精确率高(几乎无正常邮件被误删),但召回率低(部分垃圾邮件漏判);
- 阈值=0.1(宽松):召回率高(几乎无垃圾邮件漏判),但精确率低(大量正常邮件被误删)。
2. 权衡方法:阈值调整与P-R曲线分析
(1)通过阈值调整实现权衡
- 步骤1:获取模型对所有样本的预测概率(而非硬标签);
- 步骤2:遍历不同阈值(如0.1, 0.2, ..., 0.9),计算每个阈值对应的精确率和召回率;
- 步骤3:根据业务需求选择阈值(如"允许5%正常邮件被误删"→对应精确率≥95%时的最大召回率)。
(2)P-R曲线与最优阈值选择
- P-R曲线:每个点对应一个阈值的(Recall, Precision),曲线的"肘部"(Elbow Point)是兼顾两者的最优阈值(曲线从陡峭变平缓的转折点);
- 示例代码(基于1.4.12的模拟数据):
python
import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics import precision_recall_curve
# 基于之前的y_true和y_pred_prob计算不同阈值的P-R
precision, recall, thresholds = precision_recall_curve(y_true, y_pred_prob)
# 找到P-R曲线的肘部(用曲率最大法)
def find_elbow_point(recall, precision):
# 标准化召回率和精确率(0-1范围)
recall_norm = (recall - recall.min()) / (recall.max() - recall.min())
precision_norm = (precision - precision.min()) / (precision.max() - precision.min())
# 计算每个点到起点(0,1)和终点(1,0)的距离比,曲率最大点为肘部
distances = []
for r, p in zip(recall_norm, precision_norm):
# 到起点的距离
d_start = np.sqrt(r**2 + (1 - p)**2)
# 到终点的距离
d_end = np.sqrt((1 - r)**2 + p**2)
distances.append(d_start / (d_start + d_end))
# 肘部点是距离比最大的点
elbow_idx = np.argmax(distances)
return recall[elbow_idx], precision[elbow_idx], thresholds[elbow_idx-1] # thresholds比precision少1个
# 找到最优阈值
elbow_recall, elbow_precision, elbow_threshold = find_elbow_point(recall, precision)
# 绘制P-R曲线并标记肘部
plt.figure(figsize=(8, 6))
plt.plot(recall, precision, color='#ff7f0e', linewidth=2, label='P-R曲线')
plt.scatter(elbow_recall, elbow_precision, color='red', s=100, label=f'最优阈值={elbow_threshold:.2f}')
plt.xlabel('召回率(Recall)')
plt.ylabel('精确率(Precision)')
plt.title('精确率-召回率权衡与最优阈值选择')
plt.legend()
plt.grid(alpha=0.3)
plt.savefig('pr_tradeoff_elbow.png', dpi=300)
plt.show()
# 输出最优阈值对应的指标
elbow_metrics = calculate_prf1(y_true, y_pred_prob, threshold=elbow_threshold)
print(f"\n最优阈值({elbow_threshold:.2f})对应的指标:")
print(f"精确率:{elbow_metrics['Precision']:.4f},召回率:{elbow_metrics['Recall']:.4f},F1:{elbow_metrics['F1']:.4f}")3. 业务导向的权衡策略
| 业务场景 | 核心需求 | 权衡倾向 | 示例阈值选择 |
|---|---|---|---|
| 疾病诊断(如癌症筛查) | 避免漏诊(FN),允许少量误诊(FP) | 优先保证召回率,接受较低精确率 | 阈值=0.3(召回率≥99%,精确率≥60%) |
| 垃圾邮件过滤 | 避免正常邮件误删(FP),允许少量漏判(FN) | 优先保证精确率,接受较低召回率 | 阈值=0.8(精确率≥99%,召回率≥80%) |
| 电商欺诈交易拦截 | 平衡漏判(损失资金)和误判(影响用户体验) | 选择F1最大的阈值,兼顾两者 | 阈值=0.5(F1≥90%) |
| 安全漏洞检测 | 漏判后果严重(系统被攻击),误判成本低 | 极致追求召回率,忽略精确率 | 阈值=0.1(召回率≥99.9%,精确率≥30%) |
小结
- 梯度下降收敛性:通过成本曲线、梯度范数、参数变化量综合判断,避免过早停止或无效迭代;
- 模型评估体系:回归任务用MSE/RMSE,分类任务用Accuracy/Precision/Recall,倾斜数据需避免准确率陷阱;
- 过拟合解决方案:正则化(L1/L2)、早停、数据增强、模型简化,其中L2正则化(权重衰减)最常用;
- 偏差与方差诊断:高偏差(欠拟合)需增加模型复杂度,高方差(过拟合)需增加数据或增强正则化;
- 倾斜数据与P-R权衡:用PR曲线、AP值评估,根据业务需求调整阈值,优先保证核心指标(如疾病诊断的召回率);
- 数据增强与迁移学习:数据不足时,通过增强扩展数据分布,通过迁移学习复用预训练特征,大幅提升泛化能力。
模型评估与问题解决是机器学习的"闭环环节",需结合数据特点、业务需求、模型特性综合决策,避免盲目调参,通过系统化分析定位问题根源。