98.验证二叉搜索树（二叉树算法题）

98.验证二叉搜索树

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效二叉搜索树定义如下：

节点的左子树只包含严格小于当前节点的数。
节点的右子树只包含 严格大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

复制代码

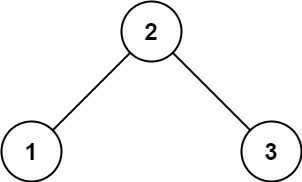
输入：root = [2,1,3]
输出：true

示例 2：

复制代码

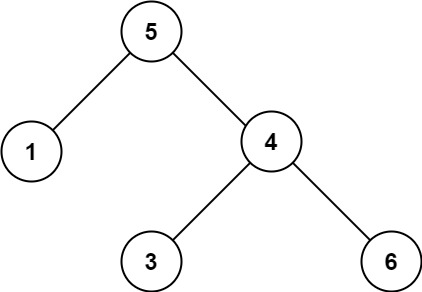
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：

树中节点数目范围在[1, 104] 内
-231 <= Node.val <= 231 - 1

递归法

可以递归中序遍历将二叉搜索树转变成一个数组，

然后只要比较一下，这个数组是否是有序的，注意二叉搜索树中不能有重复元素。

java 复制代码

/**
 * 验证二叉搜索树（Valid Binary Search Tree）
 * 
 * 核心思想：
 * 二叉搜索树（BST）的中序遍历（左 -> 根 -> 右）结果是一个严格递增的有序序列。
 * 因此，我们可以先进行中序遍历，将节点值存入列表，然后检查该列表是否严格递增。
 * 如果存在任意一个元素小于或等于前一个元素，则说明不是有效的BST。
 */
class Solution {
    
    // 用于存储中序遍历结果的列表
    // 遍历完成后，list中应为一个严格递增的序列（如果是BST）
    private List<Integer> list;

    /**
     * 主方法：判断给定的二叉树是否为有效的二叉搜索树（BST）
     * 
     * @param root 二叉树的根节点
     * @return 如果是有效的BST返回true；否则（如存在逆序或重复值）返回false
     */
    public boolean isValidBST(TreeNode root) {
        // 初始化列表，确保每次调用时list为空
        // 相当于清空上一次的结果，避免干扰
        list = new ArrayList<>();

        // 调用中序遍历方法，将整棵树的节点值按中序顺序加入list
        traversal(root);

        // 遍历list，检查是否严格递增（即：list[i] > list[i-1]）
        for (int i = 1; i < list.size(); i++) {
            // 如果当前元素小于或等于前一个元素，说明不是严格递增
            // 根据BST定义，不允许有重复值，因此不能相等
            if (list.get(i) <= list.get(i - 1)) {
                return false; // 立即返回false，不是有效BST
            }
        }

        // 所有元素都满足严格递增，说明是有效的BST
        return true;
    }

    /**
     * 辅助方法：执行中序遍历（Inorder Traversal）
     * 中序遍历顺序：左子树 -> 根节点 -> 右子树
     * 对于BST，这会生成一个从小到大排序的序列
     * 
     * @param root 当前正在遍历的节点
     */
    public void traversal(TreeNode root) {
        // 递归终止条件：如果当前节点为空，直接返回
        if (root == null) {
            return;
        }

        // 1. 先递归遍历左子树
        // 左子树的所有节点值都应小于当前根节点的值
        traversal(root.left);

        // 2. 访问当前根节点
        // 将当前节点的值添加到列表中
        // 此时，左子树已遍历完，开始处理根节点
        list.add(root.val);

        // 3. 最后递归遍历右子树
        // 右子树的所有节点值都应大于当前根节点的值
        traversal(root.right);
    }
}

迭代法

可以用迭代法模拟二叉树中序遍历，对前中后序迭代法生疏的同学可以看这两篇二叉树：听说递归能做的，栈也能做！ (opens new window)，二叉树：前中后序迭代方式统一写法(opens new window)

迭代法中序遍历稍加改动就可以了，代码如下：

java 复制代码

//使用統一迭代法
class Solution {
    public boolean isValidBST(TreeNode root) {
        Stack<TreeNode> stack = new Stack<>();
        TreeNode pre = null;
        if(root != null)
            stack.add(root);        
        while(!stack.isEmpty()){
            TreeNode curr = stack.peek();
            if(curr != null){
                stack.pop();
                if(curr.right != null)
                    stack.add(curr.right);
                stack.add(curr);
                stack.add(null);
                if(curr.left != null)
                    stack.add(curr.left);
            }else{
                stack.pop();
                TreeNode temp = stack.pop();
                if(pre != null && pre.val >= temp.val)
                    return false;
                pre = temp;
            }
        }
        return true;
    }
}