强化学习（5）多智能体强化学习

多智能体强化学习（Multi-Agent Reinforcement Learning, MARL ）与单智能体强化学习（Single-Agent Reinforcement Learning, SARL ）区别主要体现在环境的动态性 、智能体的目标 、学习的复杂性等

---

基础概念

1. 环境的动态性（Non-Stationarity）

• 单智能体（SARL）:
  • 智能体在一个相对稳定的、静态 的环境中学习。环境的动态性（即状态的转移和奖励的确定）只依赖于智能体自身的动作。
• 多智能体（MARL）:
  • 环境是非静态 的（Non-Stationary）。每个智能体的最优策略 不仅取决于环境的内在特性，还取决于其他所有智能体的策略和动作。
  • 从单个智能体的角度来看，环境（包括其他智能体）的行为是不断变化的，这使得智能体很难收敛到一个稳定的最优策略。

2. 智能体的目标与关系

关系类型	目标	示例
单智能体（SARL）	最大化其自身的累积奖励。	玩一个单人电子游戏。
多智能体（MARL）	可以有多种目标关系：
合作 (Cooperative)	所有智能体共同最大化一个共享的累积奖励。	交通灯控制、无人机编队飞行。
竞争 (Competitive)	智能体尝试最大化自身 奖励，而最小化对手的奖励（零和博弈）。	围棋、国际象棋、电子竞技中的对战。
混合 (Mixed)	智能体有各自的目标，可能部分重叠，也可能相互冲突（既合作又竞争）。	拍卖、资源共享。

还有一种关系：自我鼓励：他们只关注自己的奖励如何，并不关心别人的奖励（注意还是属于多智能体，因为每个智能体的决策还是会影响到其他智能体获得的奖励），比如股票交易系统

3. 动作空间与状态空间

• 单智能体（SARL）: 状态空间和动作空间相对较小，只包括智能体自身的。
• 多智能体（MARL）: 智能体的联合动作空间 是各个智能体动作空间的笛卡尔积（A1×A2×⋯×ANA_1 \times A_2 \times \dots \times A_NA1×A2×⋯×AN），其规模呈指数级增长 。这极大地增加了策略搜索和学习的难度，被称为维度灾难（Curse of Dimensionality）。

4. 挑战与核心问题

挑战	单智能体（SARL）	多智能体（MARL）
信度分配 (Credit Assignment)	相对简单。奖励只与自身的动作序列相关。	困难 。奖励是所有智能体联合动作的结果，难以确定每个智能体对最终结果的贡献度。
收敛性 (Convergence)	在适当条件下，通常可以保证收敛到最优策略。	难以保证 。目标是收敛到纳什均衡 (Nash Equilibrium) 或其他博弈论概念，但环境的非静态性使收敛非常困难。
可观测性 (Observability)	通常是完全可观测 或部分可观测的（POMDP），但只有自身。	经常是部分可观测的（Dec-POMDP）。智能体只能观察到环境的一部分以及/或自身的状态，无法获取所有其他智能体的内部状态和动作。
通信 (Communication)	不涉及。	重要问题。智能体是否应该、如何以及何时进行通信，以实现更好的合作或协调。

---

MARL中的几种架构

多智能体强化学习（MARL）的架构分类主要基于训练和执行阶段的信息共享程度 以及智能体之间的关系和目标。

核心上，MARL 的架构可以分为三大类：

• 完全集中式
• 完全分散式
• 集中训练/分散执行 (CTDE) 混合式

---

基于信息共享，控制程度来分类，这是 MARL 中最常用和最重要的分类方式，关注智能体在学习和实际应用中能获取多少信息，以及谁来做出最终决策。

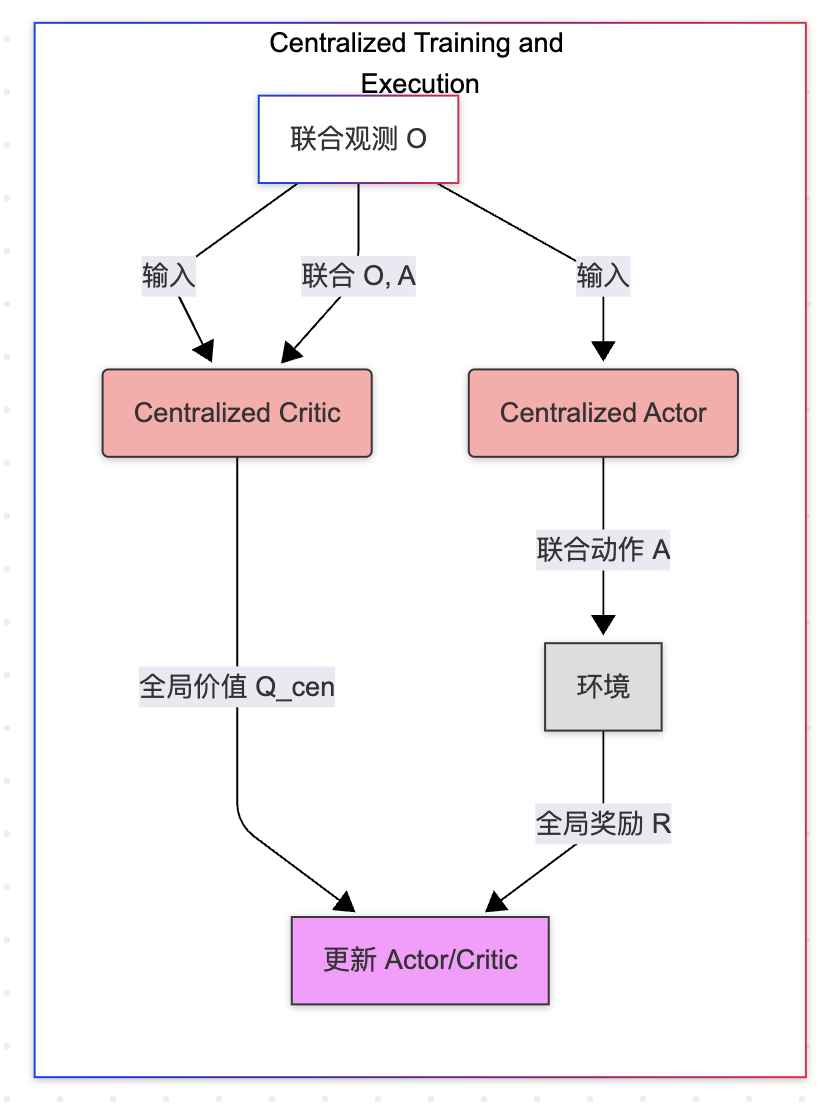
1. 完全集中式 (Centralized Training and Execution, CTE)

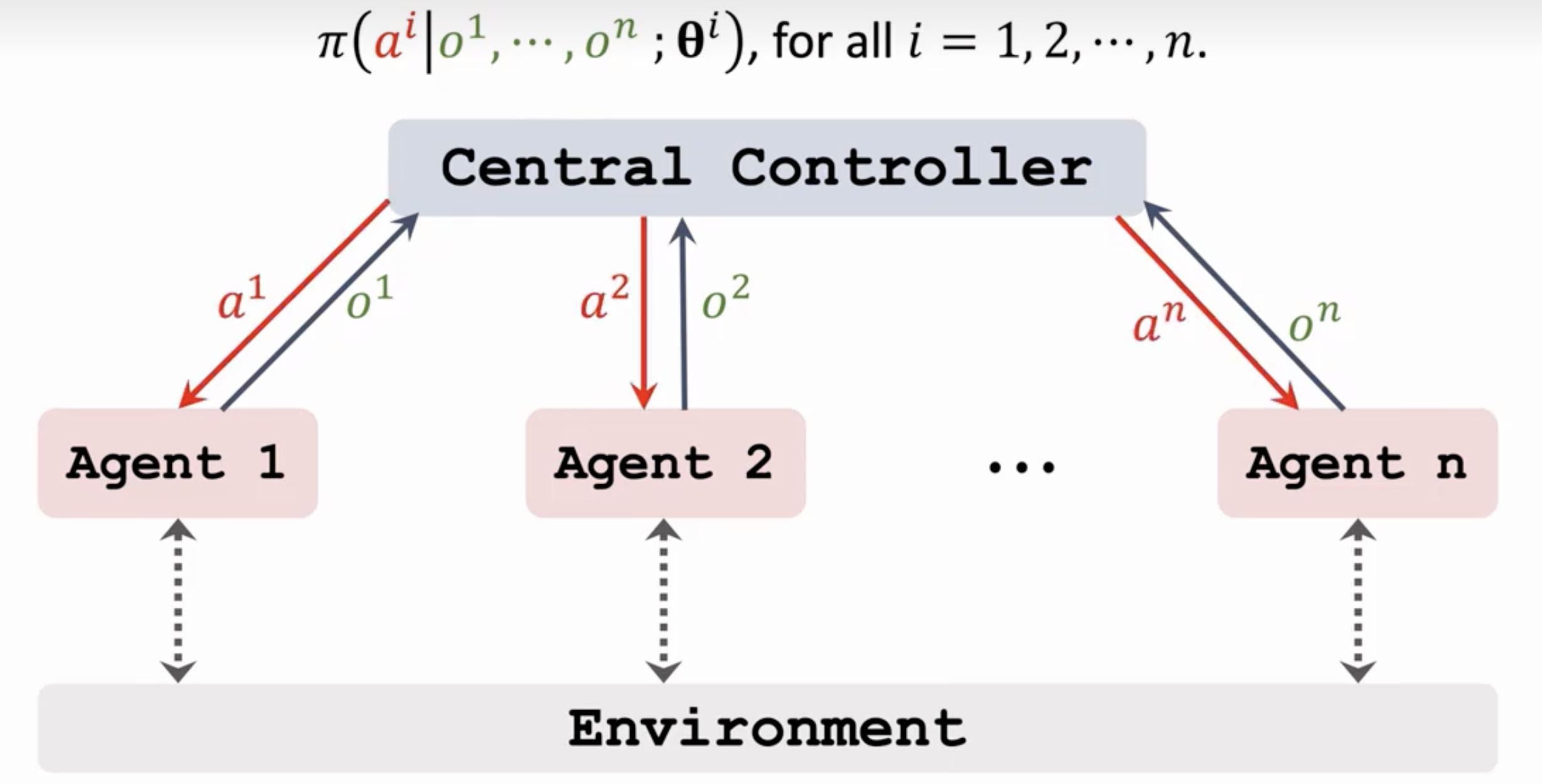
训练和执行 过程中，存在一个中央控制器（Central Controller） ，它可以访问所有智能体的观察、状态和动作，并进行全局决策

本质上，它将整个多智能体系统视为一个超级单智能体 , 可以利用全部的全局信息 ，能最容易地达到最优联合策略 。但随着智能体数量的增加，联合动作空间和状态空间呈指数级增长 （维度灾难）。鲁棒性差：一旦中央控制器失效，整个系统就会崩溃（单点故障）。现实应用受限： 许多实际场景（如机器人编队、无人驾驶）不允许在执行时进行完美的集中控制和通信。

训练与执行都是中性化的，另外这里的智能体都是可以观测到环境的，但是是各自的环境信息，并将她们的观测结果交给中央

class Centralized_Agent:
    def __init__(self, global_obs_space, global_action_space):
        # 集中式 Actor 和 Critic
        self.actor = build_nn(global_obs_space, global_action_space) # 输出联合动作 A
        self.critic = build_nn(global_obs_space + global_action_space, 1) # 估计 Q(O, A)

    def select_action(self, O):
        # 执行: 输入联合观测 O, 输出联合动作 A
        return self.actor(O) 

    def update(self, global_batch, global_reward):
        # 训练: 仅使用全局信息
        # 1. 计算 Critic 损失 (使用全局奖励 R 和联合 Q 值)
        #    TD_Error_cen = R + gamma * Q_cen(O', A') - Q_cen(O, A)
        # 2. 更新 Critic
        self.critic.update()
        # 3. 计算 Actor 损失 (最大化联合 Q 值)
        # 4. 更新 Actor
        self.actor.update()

2. 完全分散式 (Decentralized Training and Execution, DTE)

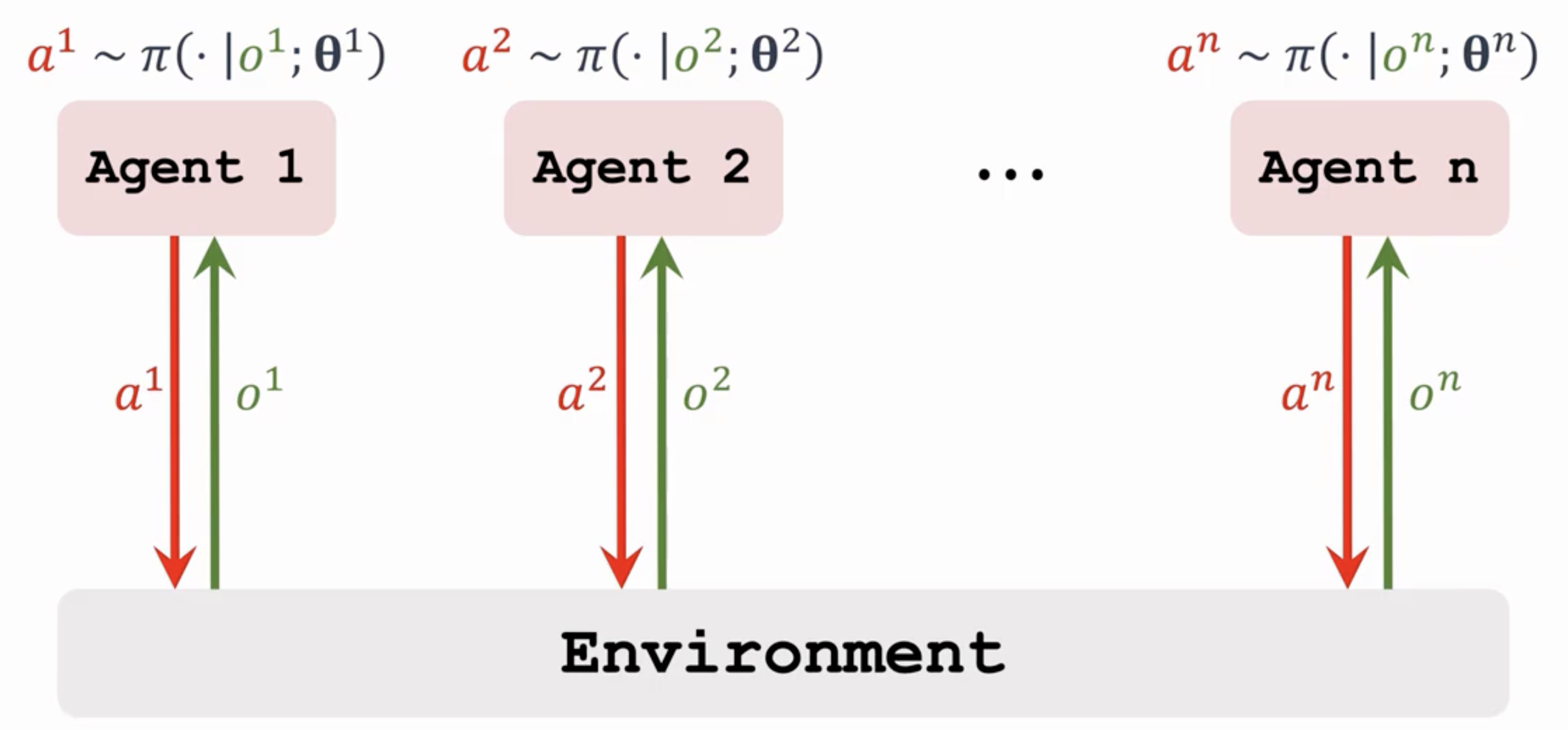
训练和执行 都完全分散。每个智能体独立学习和行动，只基于自身的局部观测 和局部奖励

其实是每个智能体都使用一个单智能体RL算法 ，但将其他智能体视为环境的一部分（即独立学习，Independent Learning），这种实现算法复杂度不随智能体数量呈指数增长，也没有单点故障等问题，但是收敛性差
根据AC我们可以给出下面的伪代码

class Independent_Agent_i:
    def __init__(self, local_obs_space, local_action_space):
        # 局部 Actor 和 Critic
        self.actor = build_nn(local_obs_space, local_action_space)
        self.critic = build_nn(local_obs_space, 1) # V(o_i) 或 Q(o_i, a_i)

    def select_action(self, o_i):
        # 执行: 只依赖局部观测
        return self.actor(o_i)

    def update(self, local_batch, global_reward):
        # 训练: 仅用局部观测 o_i 和全局奖励 R
        # 1. 计算 Critic 损失（使用全局奖励 R 作为 TD 目标）
        #    TD_Error_i = R + gamma * V_i(o'_i) - V_i(o_i)
        # 2. 更新 Critic (最小化 TD 误差)
        self.critic.update()
        # 3. 计算 Actor 损失（例如，使用局部优势函数 A_i）
        #    A_i = R + gamma * V_i(o'_i) - V_i(o_i)
        # 4. 更新 Actor (最大化带权重的 A_i)
        self.actor.update()

3. 集中训练/分散执行 (Centralized Training for Decentralized Execution, CTDE)

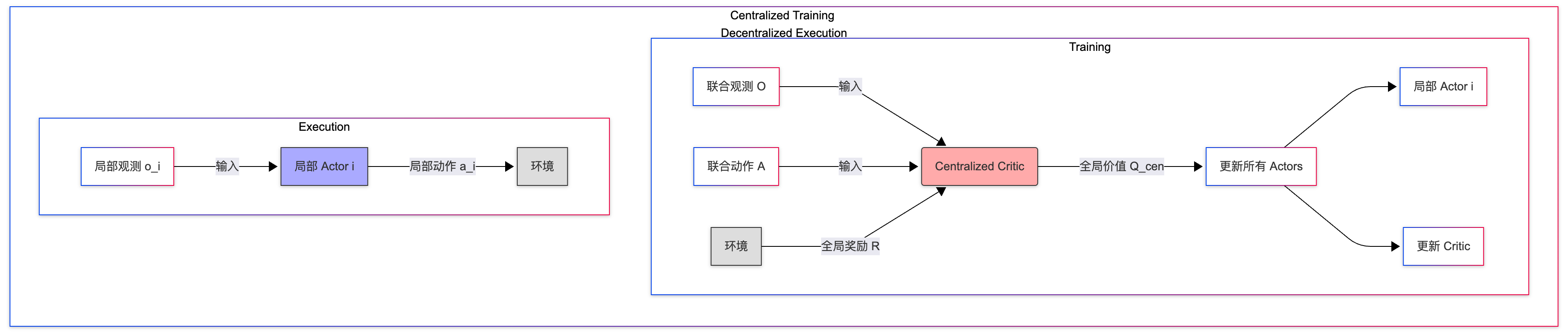
训练使用集中式 的全局信息来指导学习，根据全局信息训练多个全局 Critic（评估网络）

执行使用分散式 的局部策略，每个智能体只基于自身的局部观测来选择动作（即，使用局部 Actor/策略网络）。

class CTDE_System:
    def __init__(self, num_agents, global_obs_space, global_action_space):
        # 局部 Actor 列表
        self.actors = [build_nn(o_space, a_space) for _ in range(num_agents)]
        # 中央 Critic (输入联合 O 和 A)
        self.critic_cen = build_nn(global_obs_space + global_action_space, 1)

    def select_joint_action(self, O):
        # 执行: 分散执行，每个 Actor 只看局部 o_i
        A = [self.actors[i](O[i]) for i in range(num_agents)]
        return A

    def update(self, global_batch, global_reward):
        # 训练: 集中式 Critic 指导
        O, A, R, O_prime = global_batch
        
        # 1. 更新中央 Critic
        #    TD_Target = R + gamma * Q_cen(O', A'_target)
        #    Critic Loss = MSE(Q_cen(O, A), TD_Target)
        self.critic_cen.update()

        # 2. 更新局部 Actor i (关键步骤)
        for i in range(len(self.actors)):
            # Actor Loss = -Q_cen(O, [A_{-i}, a_i])
            #   其中 Q_cen 的 a_i 被替换为 Actor_i(o_i) 的输出
            #   这意味着 Actor_i 的梯度是通过中央 Critic 传导的
            self.actors[i].update_based_on_central_critic(self.critic_cen)

---

架构范式	训练阶段（信息）	执行阶段（信息）	关键优势	典型算法
CTE	全局（集中）	全局（集中）	理论性能上限高，能完美协调	集中式 DDPG/PPO
DTE	局部（分散）	局部（分散）	可扩展性强，鲁棒性高	IPPO, IQL
CTDE	全局（集中）	局部（分散）	兼顾高性能和实际部署要求	QMIX, MAPPO, MADDPG
H-MARL	分层/任务分解	分层/任务分解	解决长时间跨度的信度分配	基于 Option 的方法