if 语句对程序性能的影响

韩非2025-10-11 17:33

力扣关联题目：3494. 酿造药水需要的最少总时间

1. 一组代码对比

针对背景涉及的力扣题目，我使用了一种简单的方式去求解：

  1. 计算第一瓶药水的开始处理时间以及每名巫师处理完第一瓶药水的结束时间
  2. 假设从第 0 秒处理第 n 瓶药水，需要保证药水处理不阻塞的条件是，药水在第 k 名巫师处理完后，其时间不得早于第 k + 1 名巫师处理完 n-1 瓶药水的时间
  3. 根据条件2遍历出第 n 瓶药水的最早可以开始处理的时间

其中代码的20-23行就是在计算每瓶药水的最早可以开始处理的时间。

程序一：

python 复制代码 
class Solution:
    def minTime(self, skill: List[int], mana: List[int]) -> int:
        n = len(skill)
        m = len(mana)
        
        prev_row = [0] * (n + 1)
        curr_row = [0] * (n + 1)
        
        # 初始化第一行
        for j in range(1, n+1):
            prev_row[j] = prev_row[j-1] + skill[j-1] * mana[0]
        
        for i in range(1, m):
            # 计算当前行
            for j in range(1, n+1):
                curr_row[j] = curr_row[j-1] + skill[j-1] * mana[i]
            
            # 计算最大差值
            maxDelta = 0
            for j in range(n):
                delta = prev_row[j+1] - curr_row[j]
                if delta > 0:
                    maxDelta = max(maxDelta,delta)
            
            # 调整当前行
            if maxDelta > 0:
                for j in range(n+1):
                    curr_row[j] += maxDelta
            
            # 滚动数组
            prev_row, curr_row = curr_row, prev_row
        
        return prev_row[n]

程序二

python 复制代码 
class Solution:
    def minTime(self, skill: List[int], mana: List[int]) -> int:
        n = len(skill)
        m = len(mana)
        
        prev_row = [0] * (n + 1)
        curr_row = [0] * (n + 1)
        
        # 初始化第一行
        for j in range(1, n+1):
            prev_row[j] = prev_row[j-1] + skill[j-1] * mana[0]
        
        for i in range(1, m):
            # 计算当前行
            for j in range(1, n+1):
                curr_row[j] = curr_row[j-1] + skill[j-1] * mana[i]
            
            # 计算最大差值
            maxDelta = 0
            for j in range(n):
                delta = prev_row[j+1] - curr_row[j]
                if delta > maxDelta:
                    maxDelta = delta
            
            # 调整当前行
            if maxDelta > 0:
                for j in range(n+1):
                    curr_row[j] += maxDelta
            
            # 滚动数组
            prev_row, curr_row = curr_row, prev_row
        
        return prev_row[n]

上面的两组程序是针对背景题目的同样的解法，唯一的区别在于第20行到第23行部分的条件判断语句的不同。

程序一在执行测试用例时，当数据量较大时，会出现超时的错误，程序二在同样条件下，可以在时间限制内执行完全部的测试用例。

将其中有差别的代码片段摘录出来如下

片段一：

python 复制代码 
...
maxDelta = 0
for j in range(n):
    delta = prev_row[j+1] - curr_row[j]
    if delta > 0:
        maxDelta = max(maxDelta,delta)
...

片段二：

python 复制代码 
...
maxDelta = 0
for j in range(n):
    delta = prev_row[j+1] - curr_row[j]
    if delta > maxDelta:
        maxDelta = delta
...

这两个代码片段的差异主要体现在以下方面：

  1. 条件判断的不同，片段一使用的是差值与 0 的对比，片段二使用的是差值与maxDelta的对比
  2. 片段一执行多一次 max 函数调用，其中 max 函数涉及到一次判断和一次赋值操作

可以看到，其中的核心区别在于条件判断的次数和条件判断的条件。

由条件判断导致的程序性能问题，其核心原因在于：

CPU流水线中，存在对分支的预测行为，预测的分支指令会占用CPU时钟，预测失败时，流水线清除，造成时钟浪费

2. CPU 中的流水线

在计算机中，流水线的存在可以让单个的处理器并行的执行多层级的指令。如下，是一个基础的五阶段流水线示意图。

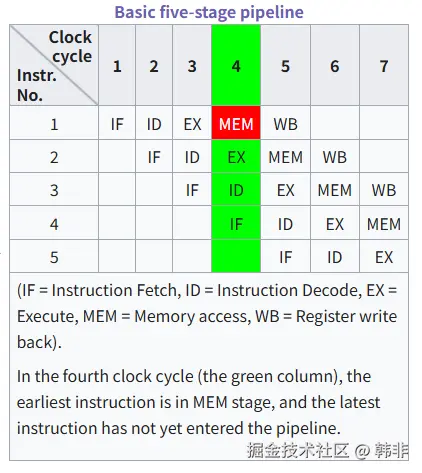
流水线中各阶段操作如下：

阶段 缩写 功能
IF Instruction Fetch 从指令缓存中取指令
ID Instruction Decode 解码指令，读取寄存器
EX Execute 执行运算（ALU操作）
MEM Memory Access 访问数据内存（加载/存储）
WB Write Back 将结果写回寄存器

对于上图，可以参考下面的示意图来进行理解

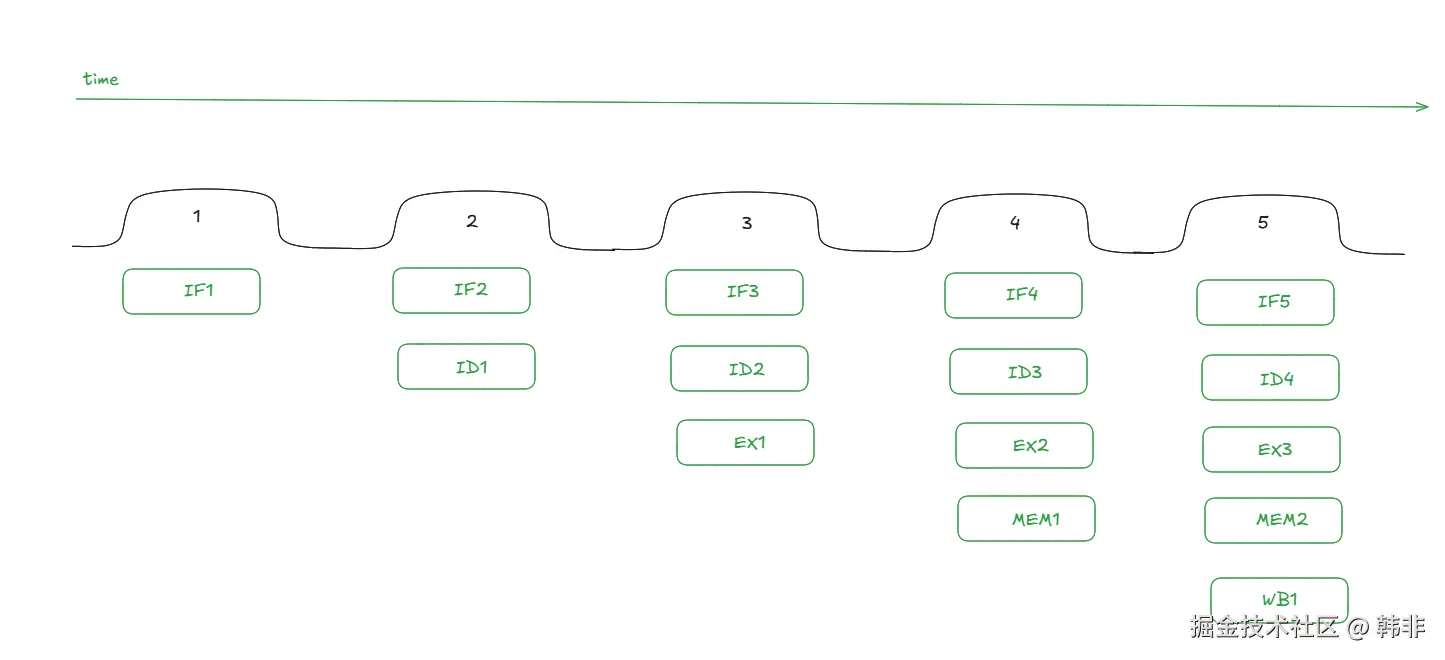
时间轴从左至右：

  • 当第一个时钟周期到达后：
    • CPU 执行 IF 操作，取缓存中的第一条指令，在第一个时钟周期结束后，将 IF 的结果放入 IF 寄存器
  • 当第二个时钟周期到达后
    • CPU 执行 IF 操作，取缓存中的第二条指令，在第二个时钟周期结束后，将 IF 的结果放回 IF 寄存器
    • CPU 执行 ID 操作，从 IF 寄存器中取第一条 IF 指令的结果，并执行解码，将结果存入 ID 寄存器
  • 当第三个时钟周期到达后
    • CPU 执行 IF 操作，取缓存中的第三条指令，在第三个时钟周期结束后，将 IF 的结果放回 IF 寄存器
    • CPU 执行 ID 操作，从 IF 寄存器中取第二条 IF 指令的结果，并执行解码，将结果存入 ID 寄存器
    • CPU 执行 EX 操作，从 ID 寄存器中取第一条 ID 指令的结果，执行操作，将结果存入 EX 寄存器
  • 当第四个时钟周期到达后
    • CPU 执行 IF 操作，取缓存中的第四条指令，在第四个时钟周期结束后，将 IF 的结果放回 IF 寄存器
    • CPU 执行 ID 操作，从 IF 寄存器中取第三条 IF 指令的结果，并执行解码，将结果存入 ID 寄存器
    • CPU 执行 EX 操作，从 ID 寄存器中取第二条 ID 指令的结果，执行操作，将结果存入 EX 寄存器
    • CPU 执行 ME 操作，从 EX 寄存器中取第一条 EX 指令的结果，执行内存数据读取，将结果存入 EX 寄存器
  • 当第五个时钟周期到达后
    • CPU 执行 IF 操作，取缓存中的第四条指令，在第四个时钟周期结束后，将 IF 的结果放回 IF 寄存器
    • CPU 执行 ID 操作，从 IF 寄存器中取第四条 IF 指令的结果，并执行解码，将结果存入 ID 寄存器
    • CPU 执行 EX 操作，从 ID 寄存器中取第三条 ID 指令的结果，执行操作，将结果存入 EX 寄存器
    • CPU 执行 ME 操作，从 EX 寄存器中取第二条 EX 指令的结果，执行内存数据读取，将结果存入 EX 寄存器
    • CPU 执行 WB 操作，从 ME 寄存器中取第一条指令的结果，将结果存入寄存器

注意：
由于信号传输时间、功耗等物理条件的限制和均衡考虑，无法在一个时钟内执行完同一条指令的所有操作，时钟与时钟之间，CPU需要进行流水线寄存器的读写操作，以此在时钟之间传递数据。

在上面的五个时钟周期过后，缓存中的第一条指令执行完成，第二条指令还差最后一个阶段，使用五阶段流水线执行指令的耗时如下：

指令序号 1 2 3 4 5
流水线耗时 5时钟 6时钟 7时钟 8时钟 9时钟
串行耗时 5时钟 10时钟 15时钟 20时钟 25时钟

由此说明，在CPU中流水线并行操作，对于计算资源利用的必要性。

为了充分的利用CPU中的各操作单元，需要尽可能的让单个时钟周期内各个操作单元处于忙碌的状态，但是对于if...else... 类的分支逻辑，在指令运行到条件判断前，无法得知后续的指令内容，如果闲置操作单元，会造成资源的浪费，为了让计算机资源尽可能的被利用，CPU中就产生了分支预测行为。

3. CPU 中的分支预测

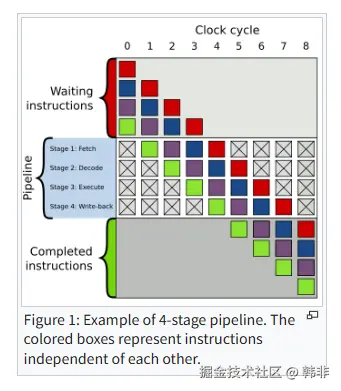
上图是一个4阶段流水线的执行示意图，其中红、蓝、紫、绿四个正方形表示的是一条指令，指令经过流水线从上向下执行，在指令等待区中就包括明确要执行的指令和CPU猜测可能需要执行的指令。

双向分支（if-else）通常通过条件跳转指令实现。条件跳转可以是"被采纳(taken)"并跳转到程序内存中的不同位置，也可以是"不被采纳"并继续紧接在条件跳转之后执行。在条件被计算出来并且条件跳转指令通过指令流水线中的执行阶段之前，无法确定条件跳转是会被采纳还是不被采纳（见图1）。

如果没有分支预测，处理器将不得不等待条件跳转指令通过执行阶段后，下一条指令才能进入流水线中的取指阶段。分支预测器试图通过猜测条件跳转最有可能被采纳还是不被采纳来避免这种时间浪费。然后，被猜测为最有可能的分支会被取指并被推测性地执行。如果之后检测到猜测错误，那么这些被推测性执行或部分执行的指令将被丢弃，流水线会从正确的分支重新开始，从而产生延迟。

在分支预测错误的情况下，所浪费的时间等于从取指阶段到执行阶段之间流水线的级数。现代微处理器往往具有相当长的流水线，因此预测错误导致的延迟在 10 到 20 个时钟周期之间。

第一次遇到条件跳转指令时，没有太多信息可以作为预测的基础。然而，分支预测器会记录分支是否被采纳的历史，因此当它遇到之前出现过多次的条件跳转时，它可以基于记录的历史进行预测。例如，分支预测器可以识别出该条件跳转"被采纳"的情况多于"不被采纳"，或者它是每隔一次被采纳。

CPU中有专门的分支预测器及算法，负责相关的分支预测工作。

scss 复制代码 
预测准确率 = (正确预测的分支数 / 总分支数) × 100%

不同预测器的表现：

  • 简单预测器：70-85%
  • 现代高级预测器：95-99%
  • 完美预测：100%

准确率每提升1%，整体性能可能提升1-2%

4. 编码风格分支预测器的影响

条件语句的特性对分支预测准确率有决定性影响。不同的条件语句模式会导致预测准确率从接近100%到接近50%的巨大差异。

4.1. 条件语句的模式分类

  • 高预测性模式（准确率 > 95%）

    • 高度偏向性条件
    c 复制代码 
    // 模式：几乎总是成立或总是不成立
if (array_size > 0) {        // 99.9% 成立
    // 处理数组
}

if (debug_mode_enabled) {    // 99.9% 不成立
    // 调试代码
}

    预测效果：简单预测器就能达到极高准确率。

    • 循环终止条件
    c 复制代码 
    // 模式：前N-1次成立，最后1次不成立
for (int i = 0; i < 100; i++) {
    // 循环体
    // 条件 i < 100: 99次成立，1次不成立
}

    预测效果：2位饱和计数器能完美预测，准确率接近100%。

    • 规律性交替
    c 复制代码 
    // 模式：固定周期交替
for (int i = 0; i < 100; i++) {
    if (i % 4 == 0) {        // 规律：每4次成立1次
        // 特殊处理
    }
}

    预测效果：局部历史预测器能学习模式，准确率高。

  • 低预测性模式（准确率 50-80%）

    • 数据依赖性条件
    c 复制代码 
    // 模式：依赖输入数据，难以预测
if (user_input > threshold) {
    // 处理
}

if (data[i] % 2 == 0) {      // 奇偶随机分布
    // 偶数处理
}

    预测效果：准确率接近随机猜测（50%）。

    • 哈希表/缓存查找
    c 复制代码 
    // 模式：依赖哈希冲突率
if (hash_table[hash(key)] != NULL) {
    // 键存在
}

    预测效果：取决于数据分布，通常60-80%。

    • 随机性条件
    c 复制代码 
    // 模式：基于随机数
if (random() < 0.3) {        // 30% 概率成立
    // 随机事件
}

    预测效果：准确率约70%（预测总选概率高的方向）。

4.2. 条件复杂度的影响

简单条件 vs 复杂条件

c 复制代码 
// 简单条件 - 易于预测
if (x > 0) { ... }

// 复杂条件 - 预测困难
if ((x > 0 && y < 10) || (z == 5 && !flag)) { ... }

影响：

  • 简单条件：模式清晰，预测器容易学习
  • 复杂条件：多个变量的组合导致模式混乱

4.3. 数据局部性的影响

数据排序的威力

c 复制代码 
// 未排序数据 - 预测困难
int data[] = {3, -1, 8, -5, 2, -9, 7, -2};
for (int i = 0; i < 8; i++) {
    if (data[i] > 0) {   // 模式: T, F, T, F, T, F, T, F
        sum += data[i];
    }
}
// 预测准确率: ~50%

// 排序后数据 - 预测容易
int sorted_data[] = {-9, -5, -2, -1, 2, 3, 7, 8};
for (int i = 0; i < 8; i++) {
    if (sorted_data[i] > 0) { // 模式: F, F, F, F, T, T, T, T
        sum += sorted_data[i];
    }
}
// 预测准确率: ~100%

4.4 编程习惯的影响

  • 可预测的代码风格

    c 复制代码 
    // 好的写法：创造可预测的模式
// 1. 将大概率路径放在前面
if (likely_success) {    // 使用likely宏提示编译器
    // 常见路径
} else {
    // 罕见路径
}

// 2. 循环展开减少分支频率
for (int i = 0; i < n; i += 4) {
    // 一次处理4个元素，减少循环条件判断
}

// 3. 使用查表代替复杂条件
static const int action_table[] = {ACTION_A, ACTION_B, ...};
action = action_table[condition1 * 4 + condition2 * 2 + condition3];

  • 难以预测的代码风格

    c 复制代码 
    // 差的写法：引入随机性
// 1. 过度使用小函数
if (is_valid(input) && should_process(input) && can_retry(input)) {
    // 每个函数调用都可能隐藏分支
}

// 2. 复杂的状态机
switch (get_complex_state()) {
    case STATE_A: ... break;
    case STATE_B: ... break; // 多个case分支难以预测
}

5. 结论

回到一开始的问题：

  • 片段一：

    python 复制代码 
    ...
maxDelta = 0
for j in range(n):
    delta = prev_row[j+1] - curr_row[j]
    if delta > 0: # 数据随机，预测成功率接近随机 50%
        maxDelta = max(maxDelta,delta) # 函数调用中存在内置的条件判断 ，增加分支预测难度
...

  • 片段二：

    python 复制代码 
    ...
maxDelta = 0
for j in range(n):
    delta = prev_row[j+1] - curr_row[j]
    if delta > maxDelta: # delta 大概率比 maxDelta 小，分支可预测程度高，且判断条件简单
        maxDelta = delta
...

参考链接

  1. CPU流水线
  2. 分支预测
相关推荐
自由的疯2 小时前
java DWG文件转图片
java·后端·架构
用户916357440952 小时前
LeetCode热题100——15.三数之和
javascript·算法
ting_zh3 小时前
导数、偏导数与梯度：机器学习数学基础
算法·基础数学
灰灰老师3 小时前
七种排序算法比较与选择[Python ]
java·算法·排序算法
秃头狂魔3 小时前
DAY1 数组一
算法
CM莫问3 小时前
推荐算法之粗排
深度学习·算法·机器学习·数据挖掘·排序算法·推荐算法·粗排
IT小番茄4 小时前
Kubernetes云平台管理实战：服务发现和负载均衡（五）
架构
rengang664 小时前
10-支持向量机（SVM）：讲解基于最大间隔原则的分类算法
人工智能·算法·机器学习·支持向量机
喜欢吃豆4 小时前
从潜在空间到实际应用：Embedding模型架构与训练范式的综合解析
python·自然语言处理·架构·大模型·微调·embedding
热门推荐
01BongoCat - 跨平台键盘猫动画工具02两千字总结：Codex 国内如何安装和使用的教程，以及如何设置中文回答03智能库存管理的需求预测模型：从业务痛点到落地代码的完整实践04GitHub 镜像站点05UV安装并设置国内源06Cursor Plan Mode：AI 终于知道先想后做了0746个Nano-banana 精选提示词，持续更新中08Linux下V2Ray安装配置指南09GitLab 零基础入门指南：从安装到项目管理全流程10一文了解国产算子编程语言 TileLang，TileLang 对国产开源生态的影响与启示