数据结构-算法C++（额外问题汇总）

木子.李3472025-10-12 21:12

目录

线性动态规划---背包问题

1. 0-1背包


洛谷题目链接

cpp 复制代码 
#include <bits/stdc++.h>
using namespace std;

int T,M;
vector<int> times;
vector<int> value;

int main(){
    cin>>T>>M;
    times.push_back(0);
    value.push_back(0);
    for(int i=0;i<M;i++){
        int t,v;
        cin>>t>>v;
        times.push_back(t);
        value.push_back(v);
    }

    vector<vector<int>>dp(M+1,vector<int>(T+1));//法一
    for(int i=1;i<M+1;i++){
        for(int j=1;j<=T;j++){
            if(times[i]<=j){
                dp[i][j]=max(dp[i-1][j],dp[i-1][j-times[i]]+value[i]);
            }else{
                dp[i][j]=dp[i-1][j];
            }
            
        }
    }

    
    cout<<dp[M][T]<<endl;
    return 0;
    
    
}


cpp 复制代码 
    vector<int>dp(T+1);//法二
    for(int i=1;i<M+1;i++){
        for(int j=T;j>=0;j--){
            dp[j]=max(dp[j],dp[j-times[i]]+value[i]);    
        }
    }

2.完全背包


题目链接

cpp 复制代码 
#include <bits/stdc++.h>
using namespace std;

int T,M;
vector<int> times;
vector<int> value;

int main(){
    cin>>T>>M;
    times.push_back(0);
    value.push_back(0);
    for(int i=0;i<M;i++){
        int t,v;
        cin>>t>>v;
        times.push_back(t);
        value.push_back(v);
    }


     vector<long long>dp(T+1);
    for(int i=1;i<M+1;i++){
        for(int j=1;j<=T;j++){
            if(times[i]<=j){
               dp[j]=max(dp[j],dp[j-times[i]]+value[i]);
            }
        }
    }

    
    cout<<dp[T]<<endl;
    return 0;
    
    
}


3.多重背包


题目链接


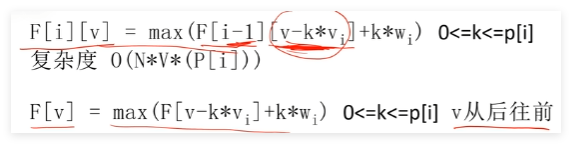
法一：

cpp 复制代码 
#include <bits/stdc++.h>
using namespace std;

int n,W;
vector<int> weight;
vector<int> value;
vector<int> counts;

int main(){
    cin>>n>>W;
    weight.push_back(0);
    value.push_back(0);
    counts.push_back(0);
    for(int i=0;i<n;i++){
        int v,w,m;
        cin>>v>>w>>m;
        value.push_back(v);
        weight.push_back(w);
        counts.push_back(m);
    }


     vector<int>dp(W+1);
    for(int i=1;i<n+1;i++){
        for(int j=W;j>=0;j--){
            for(int k=0;k<=counts[i]&&j>=k*weight[i];k++){
                //if(j>=k*weight[i])
                    dp[j]=max(dp[j],dp[j-k*weight[i]]+k*value[i]);
            }
        }
    }

    
    cout<<dp[W];
    return 0;
    
    
}

法二：二进制优化

cpp 复制代码 
#include <bits/stdc++.h>
using namespace std;

int n,W;
vector<int> weight;
vector<int> value;
int main(){
    cin>>n>>W;
    weight.push_back(0);
    value.push_back(0);
    
    for(int i=0;i<n;i++){
        int v,w,m;
        cin>>v>>w>>m;
        int tem=1;
        while(tem<=m){
            weight.push_back(tem*w);
            value.push_back(tem*v);
            m-=tem;
            tem <<=1;       
        }
        weight.push_back(m*w);
        value.push_back(m*v);
    
    }

    vector<int>dp(W+1);
    for(int i=1;i<=weight.size();i++){
        for(int j=W;j>=0&&j>=weight[i];j--){
           dp[j]=max(dp[j],dp[j-weight[i]]+value[i]);
            
        }
    }

    cout<<dp[W];
    return 0;
}

法三：单调队列优化

背包问题汇总

复杂度对比

方法 时间复杂度 空间复杂度 适用场景
朴素多重背包 O(N × W × M) O(W) 数据量小
二进制优化 O(N log M × W) O(W + N log M) 中等数据量
单调队列优化 O(N × W) O(W) 大数据量

4.混合背包

法一：分类处理

cpp 复制代码 
#include <bits/stdc++.h>
using namespace std;

// 物品结构体
struct Item {
    int T; // 耗时
    int C; // 价值
};

int main() {
    // --- 1. 输入和时间计算 ---
    string Ts, Te;
    int n;
    cin >> Ts >> Te >> n;

    int sz1 = Ts.find(':'), sz2 = Te.find(':');
    int t1 = stoi(Ts.substr(0, sz1)) * 60 + stoi(Ts.substr(sz1 + 1));
    int t2 = stoi(Te.substr(0, sz2)) * 60 + stoi(Te.substr(sz2 + 1));
    int maxT = t2 - t1;

    // --- 2. 物品分类收集 ---
    vector<Item> zero_one_items;    // 存放01背包和拆分后的多重背包物品
    vector<Item> complete_items;    // 存放完全背包物品

    for (int i = 0; i < n; i++) {
        int t, c, p;
        cin >> t >> c >> p;

        if (p == 0) {
            // 完全背包物品，直接存入
            complete_items.push_back({t, c});
        } else {
            // 01背包 (p=1) 和 多重背包 (p>1) 都走这里
            int k = 1;
            while (k <= p) {
                // 二进制拆分
                zero_one_items.push_back({t * k, c * k});
                p -= k;
                k <<= 1; // 等同于 k *= 2
            }
            if (p > 0) {
                // 处理剩余部分
                zero_one_items.push_back({t * p, c * p});
            }
        }
    }

    // --- 3. DP计算 ---
    vector<int> dp(maxT + 1, 0);

    // 步骤 A: 处理所有01背包和拆分后的多重背包物品
    // 它们都使用逆序循环，可以放在一起处理
    for (const auto& item : zero_one_items) {
        for (int j = maxT; j >= item.T; j--) {
            dp[j] = max(dp[j], dp[j - item.T] + item.C);
        }
    }

    // 步骤 B: 处理所有完全背包物品
    // 必须使用正序循环
    for (const auto& item : complete_items) {
        for (int j = item.T; j <= maxT; j++) {
            dp[j] = max(dp[j], dp[j - item.T] + item.C);
        }
    }

    // --- 4. 输出结果 ---
    cout << dp[maxT] << endl;

    return 0;
}

法二：统一为0-1背包问题

cpp 复制代码 
#include <bits/stdc++.h>
using namespace std;

int dp[1005];
int Ci[100005],Ti[100005];
int cnt=1;
int main(){
    string Ts,Te;
    int n;
    cin>>Ts>>Te>>n;
    int maxT;
    int sz1=Ts.find(':');
    int sz2=Te.find(':');
    int t1=stoi(Ts.substr(0,sz1))*60+stoi(Ts.substr(sz1+1));
    int t2=stoi(Te.substr(0,sz2))*60+stoi(Te.substr(sz2+1));
    maxT=t2-t1;


    for(int i=0;i<n;i++){
        int a,b,c;
        cin>>a>>b>>c;
        if(c==0){
            c=maxT;
        }
        c=min(c,maxT);
        int tem=1; 
        while(tem<c){
            Ci[cnt]=tem*b;
            Ti[cnt]=tem*a;
            cnt++;
            c-=tem;
            tem <<=1;       
        }
        Ci[cnt]=c*b;
        Ti[cnt]=c*a;
        cnt++;
        
    }

    for(int i=1;i<=cnt;i++){
        for(int j=maxT;j>=0&&Ti[i]<=j;j--){
            dp[j]=max(dp[j],dp[j-Ti[i]]+Ci[i]);
        }
    }
  
    cout<<dp[maxT];
    return 0;
   
}

额外资料

背包问题汇总

区间动态规划


问题链接

cpp 复制代码 
#include <bits/stdc++.h>
using namespace std;

int st[305];
int presum[305];
int main(){
    int N;
    cin>>N;
    for(int i=1;i<=N;i++){
        cin>>st[i];
        presum[i]=presum[i-1]+st[i];
    }
    int dp[305][305];
    for(int i=1;i<=N;i++){
        for(int j=i+1;j<=N;j++){
            dp[i][j]=INT_MAX;
        }
    }

     for(int len=1;len<N;len++){
        for(int l=1;l<=N-len;l++){
            int r=l+len;
            for(int k=l;k<=r-1;k++){
                dp[l][r]=min(dp[l][r],dp[l][k]+dp[k+1][r]+presum[r]-presum[l-1]);
            }    
        }    
    }

    cout<<dp[1][N]<<endl;
    return 0;
}

环形动态规划


试题链接

cpp 复制代码 
#include <bits/stdc++.h>
using namespace std;

int st[305];
int presum[305];
int main(){
    int N;
    cin>>N;
    for(int i=1;i<=N;i++){
        cin>>st[i];
        presum[i]=presum[i-1]+st[i];
    }
    for(int i=N+1;i<=2*N;i++){
        st[i]=st[i-N];
        presum[i]=presum[i-1]+st[i];
    }
    int dpmin[305][305];
    int dpmax[305][305];
    for(int i=1;i<=2*N;i++){
        for(int j=i+1;j<=2*N;j++){
            dpmin[i][j]=INT_MAX;
        }
    }

    for(int len=1;len<N;len++){
        
        for(int l=1;l<=2*N-len;l++){
            int r=l+len;
            for(int k=l;k<=r-1;k++){
                dpmin[l][r]=min(dpmin[l][r],dpmin[l][k]+dpmin[k+1][r]+presum[r]-presum[l-1]);
                dpmax[l][r]=max(dpmax[l][r],dpmax[l][k]+dpmax[k+1][r]+presum[r]-presum[l-1]);
            }    
        }    

    }
    int ansmin=INT_MAX;
    int ansmax=0;
    for(int j=1;j<=N;j++){
        ansmin=min(ansmin,dpmin[j][j+N-1]);
        ansmax=max(ansmax,dpmax[j][j+N-1]);
    }
    cout<<ansmin<<endl<<ansmax;
    
    return 0;
}

树状动态规划

问题链接

cpp 复制代码 
#include <bits/stdc++.h>
using namespace std;
struct node{
    int next;
    int to;
};

node edges[6005];
int head[6005];
int happ[6005];
int dp[6005][2];
int tol=1;
void addedges(int u,int v){
    edges[tol].to=v;
    edges[tol].next=head[u];
    head[u]=tol;
    tol++;
}

void dfs(int x){
    if(dp[x][1])return ;

    for(int i=head[x];i>0;i=edges[i].next){
        int v=edges[i].to;
        dfs(v);
        dp[x][1]+=dp[v][0];
        dp[x][0]+=max(dp[v][0],dp[v][1]);
    }
    dp[x][1]+=happ[x];
}
int main(){
    int n;
    cin>>n;

    for(int i=1;i<=n;i++){
        cin>>happ[i];
    }
    vector<bool> has_parent(n + 1, false); // 用来标记谁是子节点
    for(int i=1;i<n;i++){
        int a,b;
        cin>>a>>b;
        addedges(b,a);
        has_parent[a]=true;
    }

    // 找到根节点（没有上司的节点）
    int root = 0;
    for(int i=1; i<=n; ++i) {
        if(!has_parent[i]) {
            root = i;
            break;
        }
    }
    
    int ans=0;
    dfs(root);
    ans=max(dp[root][0],dp[root][1]);

    cout<<ans<<endl;
    return 0;
    
}

倍增

快速幂

注意两点：

  • //ans=(ans*a)%p;
    ans=((ans % p) * (a%p))%p;两者都可
  • a=(a*a)%p;此处必须要加上取模
cpp 复制代码 
#include <bits/stdc++.h>

using namespace std;
long long  a,b,p;
long long quickmi(long long a,long long b){
    long long ans=1;
    while(b){
        if(b&1){
            
            //ans=(ans*a)%p;
            ans=((ans % p) * (a%p))%p;
        }
        a=(a*a)%p;
        b>>=1;
    }
    return ans;
    
}
    
int main(){
    cin>>a>>b>>p;
    long long ans=quickmi(a,b);
   
    cout << a << "^" << b << " mod " << p << "=" << ans << endl;
    return 0;
}

试题链接

ST表

区间最大值查询

cpp 复制代码 
#include <bits/stdc++.h>
using namespace std;
int logn[100005];
int dp[100005][55];//dp[i][j]:以i为左边界，长度为2^j的区间内的最大值
int main(){
    int N,M;
    cin>>N>>M;
    cin>>dp[1][0];
    logn[1]=0;
    for(int i=2;i<=N;i++){
        cin>>dp[i][0]; 
        logn[i]=logn[i>>1]+1;//计算logx
    }

    for(int j=1;j<=logn[N];j++){
        for(int i=1;i<=N-(1<<j)+1;i++){
            dp[i][j]=max(dp[i][j-1],dp[i+(1<<(j-1))][j-1]);
            
        }
    }

     

    int l,r;
    while(M--){
        cin>>l>>r;
        //int len=0;
        // while(pow(2,len)<(r-l+1)){
        //     len++;
        // }
        // if(pow(2,len)>(r-l+1))len--;

        int len=logn[r-l+1];//换取最大长度
        int ans=max(dp[l][len],dp[r-(1<<len)+1][len]);//分别以l为左边界、r为右边界，长度为2^len的区间最大值
        cout<<ans<<endl;
    }
    return 0;
    
    
}

试题链接

参考资料

课程资料

相关推荐
yolo_guo3 小时前
sqlite 使用: 03-问题记录：在使用 sqlite3_bind_text 中设置 SQLITE_STATIC 参数时，处理不当造成的字符乱码
linux·c++·sqlite
花心蝴蝶.3 小时前
API签名认证算法全解析
算法
兮山与3 小时前
算法6.0
算法
代码对我眨眼睛3 小时前
739. 每日温度 LeetCode 热题 HOT 100
算法·leetcode
程序员莫小特3 小时前
老题新解|计算2的N次方
开发语言·数据结构·算法·青少年编程·信息学奥赛一本通
wearegogog1235 小时前
基于块匹配的MATLAB视频去抖动算法
算法·matlab·音视频
十重幻想5 小时前
PTA6-1 使用函数求最大公约数（C）
c语言·数据结构·算法
青岛少儿编程-王老师5 小时前
CCF编程能力等级认证GESP—C++5级—20250927
java·数据结构·c++
大千AI助手6 小时前
蛙跳积分法：分子动力学模拟中的高效数值积分技术
算法·积分·数值积分·蛙跳积分法·牛顿力学系统·verlet积分算法
热门推荐
01BongoCat - 跨平台键盘猫动画工具02智能库存管理的需求预测模型：从业务痛点到落地代码的完整实践03两千字总结：Codex 国内如何安装和使用的教程，以及如何设置中文回答04GitHub 镜像站点05UV安装并设置国内源062025羊城杯网络安全大赛 wp07Linux下V2Ray安装配置指南0846个Nano-banana 精选提示词，持续更新中09Cursor Plan Mode：AI 终于知道先想后做了10Spring Boot 实现微信登录，So Easy !